文档内容
巴中市普通高中 2020 级 “零诊” 考试
数学(文科)
( 满分 150 分 120 分钟完卷)
注意事项:
1.答题前,考生务必将自己的姓名、班级、考号填写在答题卡规定的位置.
2.答选择题时请使用2B铅笔将答题卡上对应题目的答案标号涂黑;非选择题答题时必须用
0.5毫米黑色墨迹签字笔,将答案书写在答题卡规定的位置,在规定的答题区域以外答题无效,在试
题卷上答题无效.
3.考试结束后,考生将答题卡交回.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个
是符合题目要求的.
1.设全集U={1,2,3,4,5},若集合M满足∁ M={1,2},则( )
U
A. 2∈M B. 3∈M C. 4∉M D. 5∉M
2. 若复数z满足i⋅z=3−4i(i为虚数单位),则复数z的虚部为( )
A. −3i B. 3i C. −3 D. 3
3. 已知直线l :x+ y−1=0,l :x+m2y=0,则“m=1”是“l //l ”的( )
1 2 1 2
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
y2
4. 已知双曲线 x2− =1(b>0) 的焦点到渐近线的距离为 2 , 则双曲线的离心率为( )
b2
学科网(北京)股份有限公司2❑√3 ❑√5
A. B. C. ❑√2 D. ❑√5
3 2
5. 已知 α,β 是两个不同的平面, m,n 是两条不重合的直线, 则下列命题中正确的是 ( )
A. 若 m⊥α,m⊥n, 则 n//α
B. 若 m//β,α⋂β=n,m⊥n, 则 α⊥β
C. 若 α⊥β,m⊥α,n⊥β, 则 m⊥n
D. 若 α⊥β,α∩β=n,m⊥n, 则 m⊥β
6.已知角θ的顶点在坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b)且
3
cos2θ=− ,则|OB)=( )
5
A. ❑√5 B. 2❑√3 C. 4 D. 2❑√5
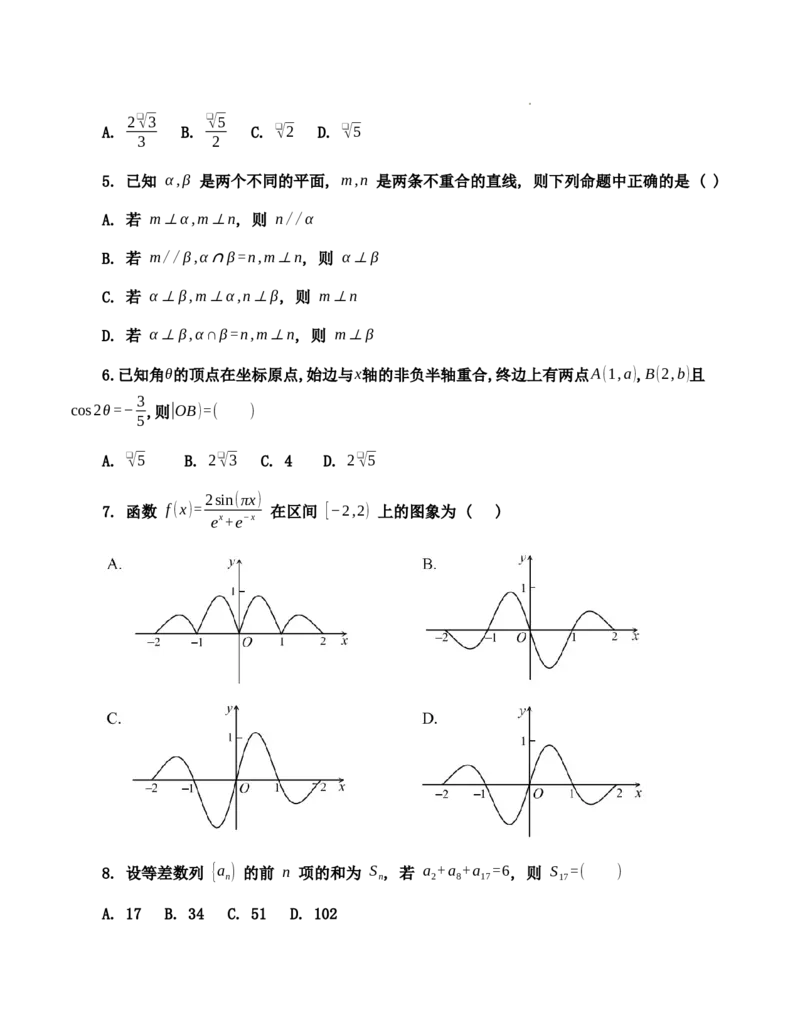
2sin(πx)
7. 函数 f (x)= 在区间 [−2,2) 上的图象为 ( )
ex+e−x
8. 设等差数列 {a ) 的前 n 项的和为 S , 若 a +a +a =6, 则 S =( )
n n 2 8 17 17
A. 17 B. 34 C. 51 D. 102
学科网(北京)股份有限公司9.已知点D在直角△ABC的斜边BC上,若AB=2,AC=3,则⃗AD⋅⃗BC的取值范围为()
A.[−4,9) B. [0,9) C. [0,4) D. [−2,3)
( π) π
10.设ω>0,若函数y=cos ωx+ 的图象向左平移 个单位长度后与函数y=sinωx的图象重
3 3
合,则ω的最小值为( )
11 7 5 3
A. B. C. D.
2 2 2 2
11.已知函数f (x)=x3−3x+1,则下列关于函数f (x)性质描述错误的是( )
A. 函数 f (x) 有两个极值点
B. 函数 f (x) 有三个零点
C. 点 (0,1) 是曲线 y=f (x) 的对称中心
D. 直线 x+ y=0 与曲线 y=f (x) 的相切
12. 已知 2a=6,3b=12,4c=20, 则( )
A. a>b>c
B. c>a>b
C. b>a>c
D. c>b>a
二、填空题: 本大题共 4 个小题, 每小题 5 分, 共 20 分.
13. 抛物线 y2=4x 的焦点 F 到其准线 l 的距离为 .
14. 某智能机器人的广告费用 x (万元)与销售额 y (万元)的统计数据如下表:
学科网(北京)股份有限公司广告费用x(万元)
2 3 5 6
销售额y(万元)
28 31 41 48
根据上表可得回归方程 ^y=5x+a^ ,据此模型预报广告费用为 8 万元时销售额为 万
元.
15. 在三棱锥A−BCD 中, BD⊥平面 ADC,BD=2,AB=2❑√2,AC=BC=2❑√5, 则三棱锥
A−BCD 的外接球的体积为 .
16. 在 △ABC 中, 角 A,B,C 的对边分别为 a,b,c, 若 ccosB+bcosC=2acosA, 则 A=
, sinBsinC 的取值范围为 . ( 第一空 2 分, 第二空 3 分)
三、解答题: 共 70 分. 解答应写出文字说明、证明过程或演算步骤. 第 17−21 题为必考
题, 每个试题考生都必须作答. 第 22、23 题为选考题, 考生根据要求作答.
(一) 必考题: 60 分.
17. ( 12 分)
已知数列 {a ) 的前 n 项和为 S , 若 a =2, 且 S −2S =2.
n n 1 n+1 n
( 1 ) 求数列 {a ) 的通项公式;
n
( 2 ) 若数列 {b ) 满足 b =na , 求数列 {b ) 的前 n 项和 T .
n n n n n
18. ( 12 分)
自《“健康中国 2030” 规划纲要》颁布实施以来, 越来越多的市民加入到绿色运动 “健
步走” 行列以提高自身的健康水平与身体素质. 某调查小组为了解本市不同年龄段的 市民在一
周内健步走的情况, 在市民中随机抽取了 200 人进行调查, 部分结果如下表所示,
学科网(北京)股份有限公司3
其中一周内健步走少于 5 万步的人数占样本总数的 ,45 岁以上(含 45 岁) 的人数占
10
3
样 本总数的 .
5
一周内健步走≥5万步 一周内健步走<5万步 总计
45岁以上(含45岁) 90
45岁以下
总计 200
(1)请将题中表格补充完整, 并判断是否有 90%的把握认为该市市民一周内健步走的步数
与年龄有关;
(2) 现从样本中 45 岁以上(含 45 岁)的人群中按一周内健步走的步数是否少于 5 万 步用
分层抽样法抽取 8 人做进一步访谈, 然后从这 8 人中随机抽取 2 人填写调查问卷, 求 抽取的
2 人中恰有一人一周内健步走步数不少于 5 万步的概率.
附:
P(K²≥K ) 0.150 0.100 0.050 0.025
0
K 2.072 2.706 3.841 5.024
0
n(ad−bc) 2
K2= , 其中n=a+b+c+d.
(a+b)(c+d)(a+c)(b+d)
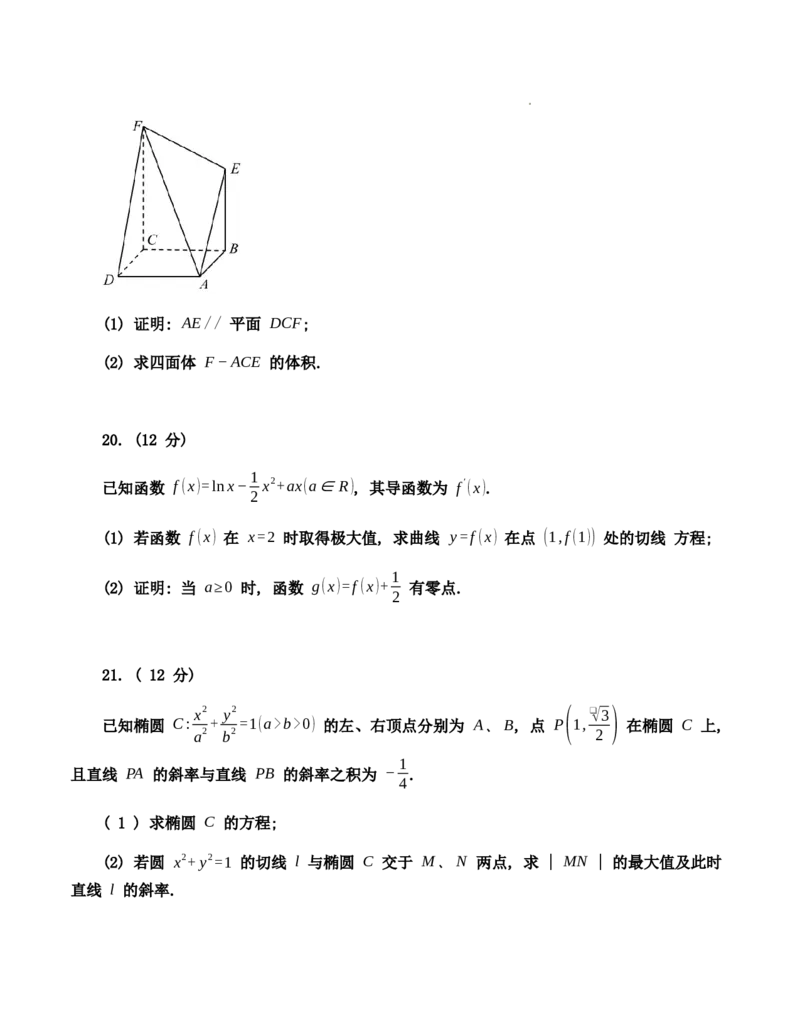
19. ( 12 分 )
如图, 正方形 ABCD 和直角梯形 BEFC 所在平面互相垂直,BE⊥BC,BE//CF, 且
AB=BE=2,CF=3.
学科网(北京)股份有限公司(1) 证明: AE// 平面 DCF;
(2) 求四面体 F−ACE 的体积.
20. (12 分)
1
已知函数 f (x)=lnx− x2+ax(a∈R), 其导函数为 f′(x).
2
(1) 若函数 f (x) 在 x=2 时取得极大值, 求曲线 y=f (x) 在点 (1,f (1)) 处的切线 方程;
1
(2) 证明: 当 a≥0 时, 函数 g(x)=f (x)+ 有零点.
2
21. ( 12 分)
x2 y2 ( ❑√3)
已知椭圆 C: + =1(a>b>0) 的左、右顶点分别为 A、B, 点 P 1, 在椭圆 C 上,
a2 b2 2
1
且直线 PA 的斜率与直线 PB 的斜率之积为 − .
4
( 1 ) 求椭圆 C 的方程;
(2) 若圆 x2+ y2=1 的切线 l 与椭圆 C 交于 M、N 两点, 求 | MN | 的最大值及此时
直线 l 的斜率.
学科网(北京)股份有限公司(二)选考题: 共 10 分. 请考生在第 22、23 题中任选一题作答. 如果多做, 则按所做的
第一题记分.
22.【选修 4-4: 坐标系与参数方程 】(10 分)
π
在直角坐标系 xOy 中, 直线 l 经过点 P(1,0), 倾斜角为 . 以坐标原点 O 为极点, 以
6
( π)
x 轴的正半轴为极轴, 建立极坐标系, 曲线 C 的极坐标方程为 ρ=2❑√2cos θ− .
4
(1) 求直线 l 的参数方程和曲线 C 的直角坐标方程;
(2) 设直线 l 与曲线 C 相交于 A,B 两点, 求 |PA)+|PB) 的值.
23.【选修 4-5 不等式选讲】(10 分)
已知函数 f (x)=|2x−3)+|2x+3).
(1) 解不等式 f (x)≤8;
1 1 1 M
(2) 设函数 f (x) 的最小值为 M, 若正数 a,b,c 满足 + + = , 证明 :
a 2b 3c 6
a+2b+3c≥9.
学科网(北京)股份有限公司【公众号:一枚试卷君】 微信号:aa1ss33555
资料免费下载系列
1.高一到高三试题全套免费下载
领取方法:关注公众号【一枚试卷君】后台回复“高中试题”即可免费下载
总共9808份电子版资料8.65个G,包含高一到高三!
免费QQ群系列
——————————————————————————————————————————
高三VIP群~主要针对群体:2023届高考生
提供的资料内容
1、 2021年9月份到2022年6月份各地名校卷、各地联考卷、一二模
模拟卷
2、 2022年8月份到2023年6月份各地名校卷、各地联考卷、一二模
模拟卷(实时更新)
3、各科知识点总结、笔记、答题模板、专题讲义训练、全套复习讲义
服务形式
QQ群+网盘群形式,群里面里每天的资料通过群文件来更新,方便
各位下载打印,每个星期的资料会汇总进网盘群,提供下载。最新资料依
旧采用每日QQ群里面直接文件形式更新。
|入群费用|
9科全部模拟试卷+复习资料等等内容
原价99 元
9月31号以前入群超级特价49 元
学科网(北京)股份有限公司