文档内容
注意事项:
1. 本试卷分为两部分, 第一部分为选择题, 第二部分为非选择题.
2. 考生领到试卷后, 须按规定在试卷上填写姓名、准考证号,并在答题卡上填涂对应的试卷类
型信息.
3. 所有解答必须填写在答题卡上指定区域内. 考试结束后, 将本试卷和答题卡一并交回.
第一部分(共 50分)
一、选择题:在每小题给出的四个选项中,只有一项符合题目要求(本大题共10小题,
每小题5分,共50 分)
1. 设全集为R, 函数 f(x)= 1-x2 的定义域为M, 则C M 为
R
(A) [-1,1] (B) (-1,1)
(C) (-¥,-1]È[1,+¥) (D) (-¥,-1)È(1,+¥)
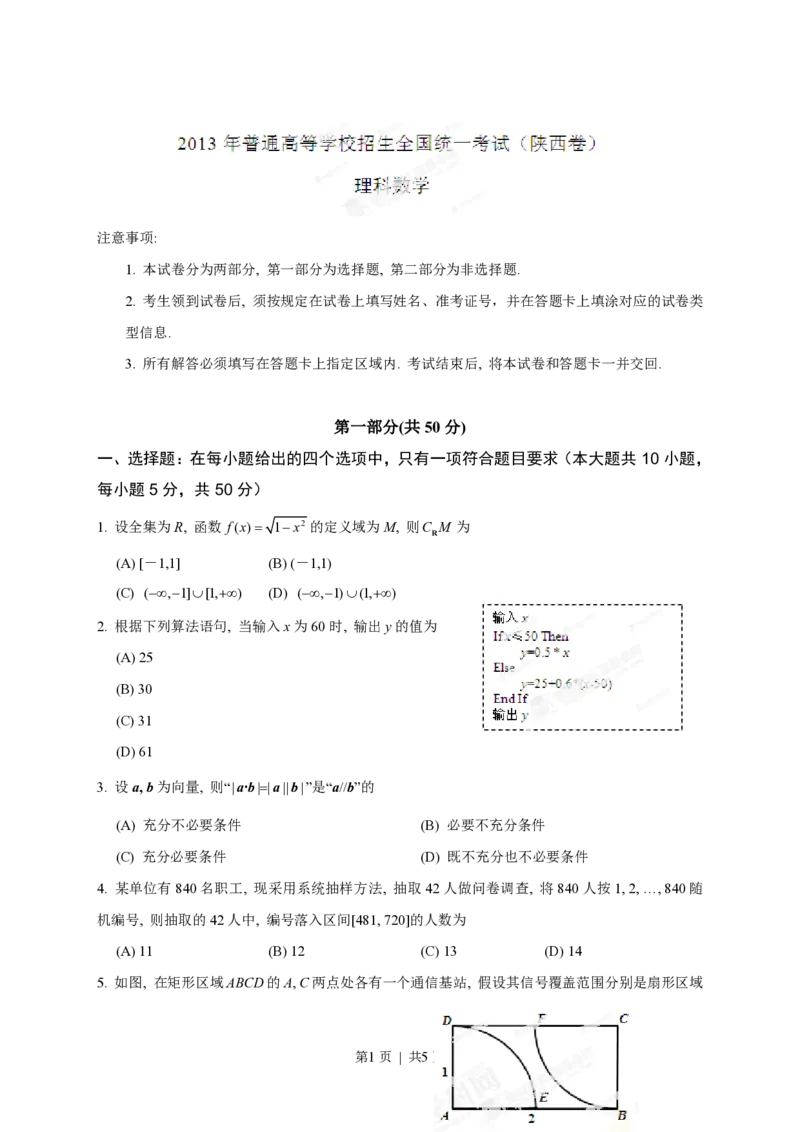
2. 根据下列算法语句, 当输入x为60时, 输出y的值为
(A) 25
(B) 30
(C) 31
(D) 61
3. 设a, b为向量, 则“|a·b|=|a||b|”是“a//b”的
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充分必要条件 (D) 既不充分也不必要条件
4. 某单位有840名职工, 现采用系统抽样方法, 抽取42人做问卷调查, 将840人按1, 2, …, 840随
机编号, 则抽取的42人中, 编号落入区间[481, 720]的人数为
(A) 11 (B) 12 (C) 13 (D) 14
5. 如图, 在矩形区域ABCD的A, C两点处各有一个通信基站, 假设其信号覆盖范围分别是扇形区域
第1页 | 共5页ADE和扇形区域CBF(该矩形区域内无其他信号来源, 基站工作正常). 若在该矩形区域内随机地选
一地点, 则该地点无信号的概率是
p p
(A)1- (B) -1
4 2
p p
(C) 2- (D)
2 4
6. 设z , z 是复数, 则下列命题中的假命题是
1 2
(A) 若|z -z |=0, 则z =z (B) 若z =z , 则z =z
1 2 1 2 1 2 1 2
(C) 若|z =z |, 则z·z =z ·z (D) 若|z =z |, 则z2 =z 2
1 2 1 1 2 2 1 2 1 2
7. 设△ABC的内角A, B, C所对的边分别为a, b, c, 若 bcosC+ccosB=asinA, 则△ABC的形状为
(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定
ìæ 1ö 4
ïçx- ÷ , x<0,
8. 设函数 f(x)=íè xø , 则当x>0时, f[f(x)]表达式的展开式中常数项为
ï
î - x, x³0.
(A) -20 (B) 20 (C) -15 (D) 15
9. 在如图所示的锐角三角形空地中, 欲建一个面积不小于300m2的内接矩形花园(阴影部分), 则其
边长x(单位m)的取值范围是
(A) [15,20] (B) [12,25] 40m
x
(C) [10,30] (D) [20,30]
10. 设[x]表示不大于x的最大整数, 则对任意实数x, y, 有 40m
(A) [-x] = -[x] (B) [2x] = 2[x]
(C) [x+y]≤[x]+[y] (D) [x-y]≤[x]-[y]
第二部分(共 100 分)
二、填空题:把答案填写在答题卡相应题号后的横线上(本大题共 5 小题,每小题 5
分,共25分)
第2页 | 共5页x2 y2 5
11. 双曲线 - =1的离心率为 , 则m等于 .
16 m 4
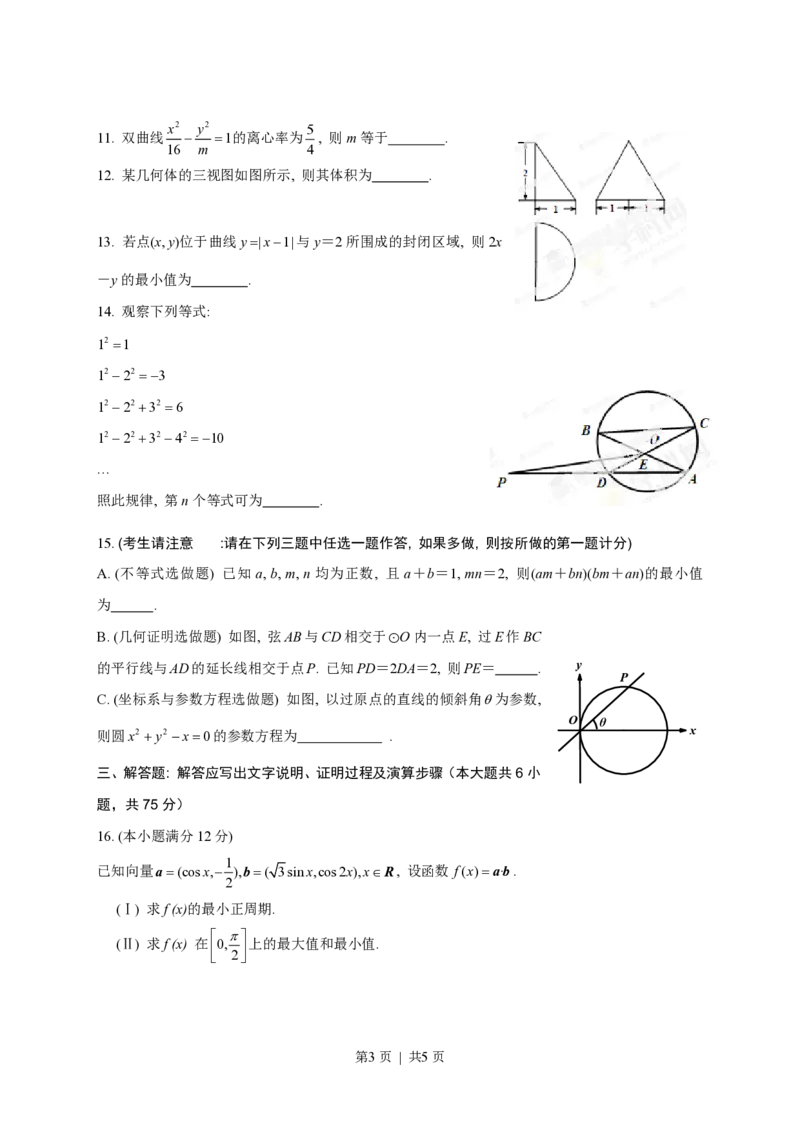
12. 某几何体的三视图如图所示, 则其体积为 .
13. 若点(x, y)位于曲线y=|x-1|与y=2所围成的封闭区域, 则2x
-y的最小值为 .
14. 观察下列等式:
12 =1
12 -22 =-3
12 -22 +32 =6
12 -22 +32 -42 =-10
…
照此规律, 第n个等式可为 .
15. (考生请注意 :请在下列三题中任选一题作答, 如果多做, 则按所做的第一题计分)
A. (不等式选做题) 已知 a, b, m, n 均为正数, 且 a+b=1, mn=2, 则(am+bn)(bm+an)的最小值
为 .
B. (几何证明选做题) 如图, 弦AB与CD相交于 O内一点E, 过E作BC
e
的平行线与AD的延长线相交于点P. 已知PD=2DA=2, 则PE= . y
P
C. (坐标系与参数方程选做题) 如图, 以过原点的直线的倾斜角q为参数,
O θ
则圆x2 + y2 -x=0的参数方程为 . x
三、解答题: 解答应写出文字说明、证明过程及演算步骤(本大题共6小
题,共75分)
16. (本小题满分12分)
1
已知向量a=(cosx,- ),b=( 3sinx,cos2x),xÎR, 设函数 f(x)=a·b.
2
(Ⅰ) 求f (x)的最小正周期.
é pù
(Ⅱ) 求f (x) 在 0, 上的最大值和最小值.
ê ú
ë 2û
第3页 | 共5页17. (本小题满分12分)
设{a }是公比为q的等比数列.
n
(Ⅰ) 推导{a }的前n项和公式;
n
(Ⅱ) 设q≠1, 证明数列{a +1}不是等比数列.
n
18. (本小题满分12分)
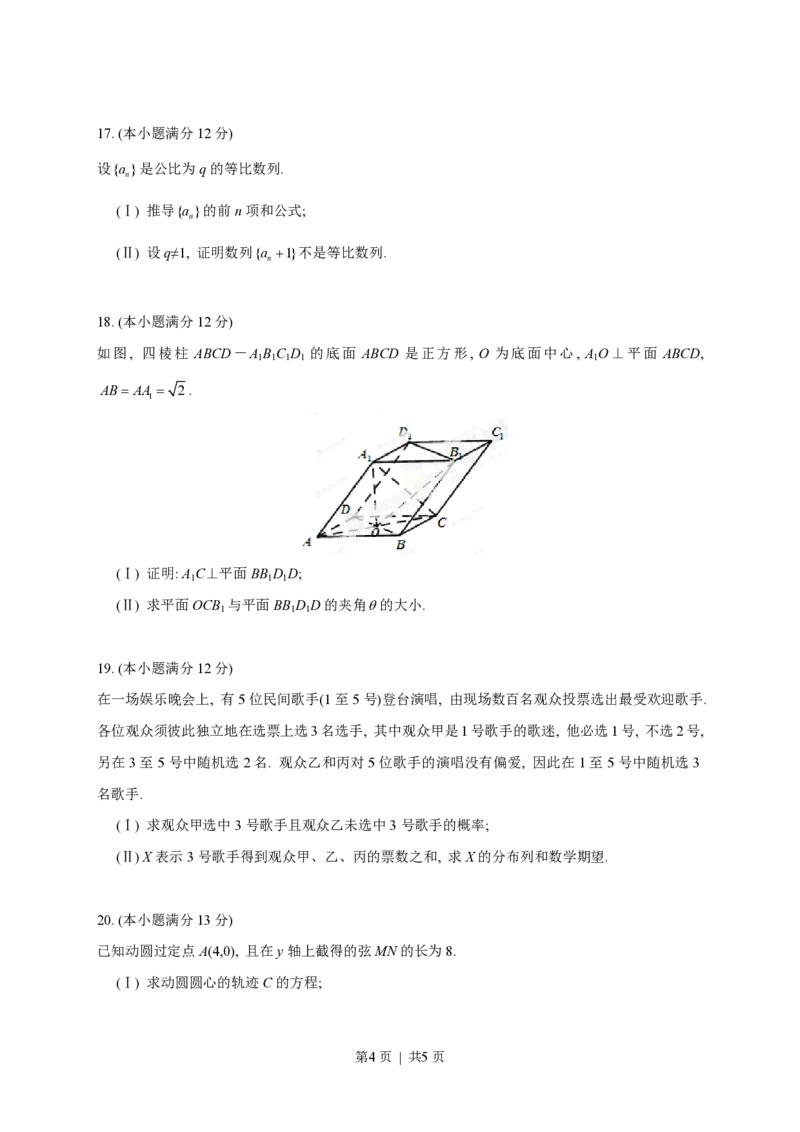
如图, 四棱柱 ABCD-A B C D 的底面 ABCD 是正方形, O 为底面中心, A O⊥平面 ABCD,
1 1 1 1 1
AB= AA = 2.
1
(Ⅰ) 证明: A C⊥平面BB D D;
1 1 1
(Ⅱ) 求平面OCB 与平面BB D D的夹角q的大小.
1 1 1
19. (本小题满分12分)
在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手.
各位观众须彼此独立地在选票上选3名选手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号,
另在3至5号中随机选2名. 观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3
名歌手.
(Ⅰ) 求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(Ⅱ) X表示3号歌手得到观众甲、乙、丙的票数之和, 求X的分布列和数学期望.
20. (本小题满分13分)
已知动圆过定点A(4,0), 且在y轴上截得的弦MN的长为8.
(Ⅰ) 求动圆圆心的轨迹C的方程;
第4页 | 共5页(Ⅱ) 已知点B(-1,0), 设不垂直于x轴的直线l与轨迹C交于不同的两点P, Q, 若x轴是ÐPBQ
的角平分线, 证明直线l过定点.
21. (本小题满分14分)
已知函数 f(x)=ex,xÎR.
(Ⅰ) 若直线y=kx+1与f (x)的反函数的图像相切, 求实数k的值;
(Ⅱ) 设x>0, 讨论曲线y=f (x) 与曲线y=mx2(m>0) 公共点的个数.
f(a)+ f(b) f(b)- f(a)
(Ⅲ) 设a