文档内容
特别提醒:
zhangwlx
(14)、(15)、(16)三题为选做题,请从中任选两题作答,若三题全做,则按前
两题给分.
一.选择题:本大题共 10小题,每小题 5分,共50分.在每小题给出的四个
备选项中,只有一个选项是符合题目要求的.
zhangwlx
1、已知集合 ,集合 , ,则
(A) (B) (C) (D)
2、命题“对任意 ,都有 ”的否定为
(A)对任意 ,使得 (B)不存在 ,使得
(C)存在 ,都有 (D)存在 ,都有
3、 ( )的最大值为
(A)9 (B) (C)3 (D)
4、以下茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).
甲组 乙组
9 0 9
2 1 5 8
7 4 2 4
已知甲组数据的中位数为15,乙组数据的平均数为16.8,则 、 的值分别为
(A)2、5 (B)5、5
(C)5,8 (D)8,8zhangwlx
5、某几何体的三视图如题(5)图所示,则该几何体的
体积为
(A)
(B)
(C)200
(D)240
第1页 | 共6页zhangwlx
6、若 ,则函数 两个零点分
别位于区间
(A) 和 内 (B) 和 内
(C) 和 内 (D) 和 内
7、已知圆 : ,圆 : , 、 分别是
圆 、 上的动点, 为 轴上的动点,则 的最小值为
(A) (B) (C) (D)
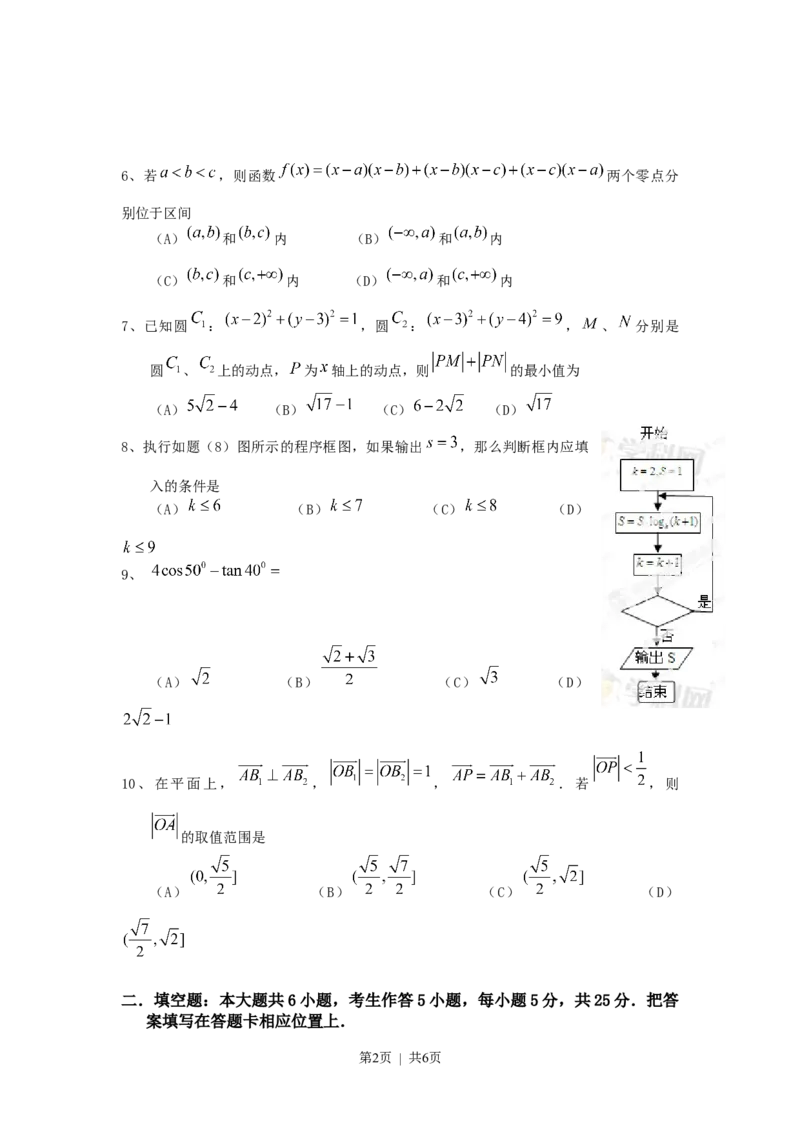
8、执行如题(8)图所示的程序框图,如果输出 ,那么判断框内应填
入的条件是
(A) (B) (C) (D)
9、 zhangwlx
(A) (B) (C) (D)
10、在平面上, , , .若 ,则
的取值范围是
(A) (B) (C) (D)
二.填空题:本大题共6小题,考生作答5小题,每小题5分,共25分.把答
案填写在答题卡相应位置上.
第2页 | 共6页11、已知复数 ( 是虚数单位),则 .zhangwlx
12、已知 是等差数列, ,公差 , 为其前 项和,若 、 、 称等
比数列,则 .
13、从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨
科、脑外科和内科医生都至少有1人的选派方法种数是 (用数字作答).
考生注意:(14)、(15)、(16)三题为选做题,请从中任选两题作答,若
三题全做,则按前两题给分.
14、如题(14)图,在△ 中, , , ,过 作△
的外接圆的切线 , ⊥ , 与外接圆交于点 ,则 的长为 .
zhangwlx
15、在直角坐标系 中,以原点 为极点, 轴的正半轴为极轴建立
极坐标系.若极坐标方程为 的直线与曲线 ( 为参数)
相交于 、 两点,则 .
16、若关于实数 的不等式 无解,则实数 的取值范围是 .
zhangwlx
三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演
算步骤.
17、(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分)
设 ,其中 ,曲线 在点(1, )处的切线
与 轴相较于点(0,6).
(Ⅰ)确定 的值;
(Ⅱ)求函数 的单调区间与极值.
18、(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分)
某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有 3个红
球与4个白球的袋中任意摸出3个球,再从装有1个篮球与2个白球的袋中任意摸出1
个球,根据摸出4个球中红球与篮球的个数,设一、二、三等奖如下:zhangwlx
奖级 摸出红、蓝球个数 获奖金额
一等奖 3红1蓝 200元
二等奖 3红0蓝 50元
三等奖 2红1蓝 10元
其余情况无奖且每次摸奖最多只能获得一个奖级.
第3页 | 共6页(Ⅰ)求一次摸球恰好摸到1个红球的概率;
(Ⅱ)求摸奖者在一次摸奖中获奖金额 的分布列与期望 .
19、(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分)
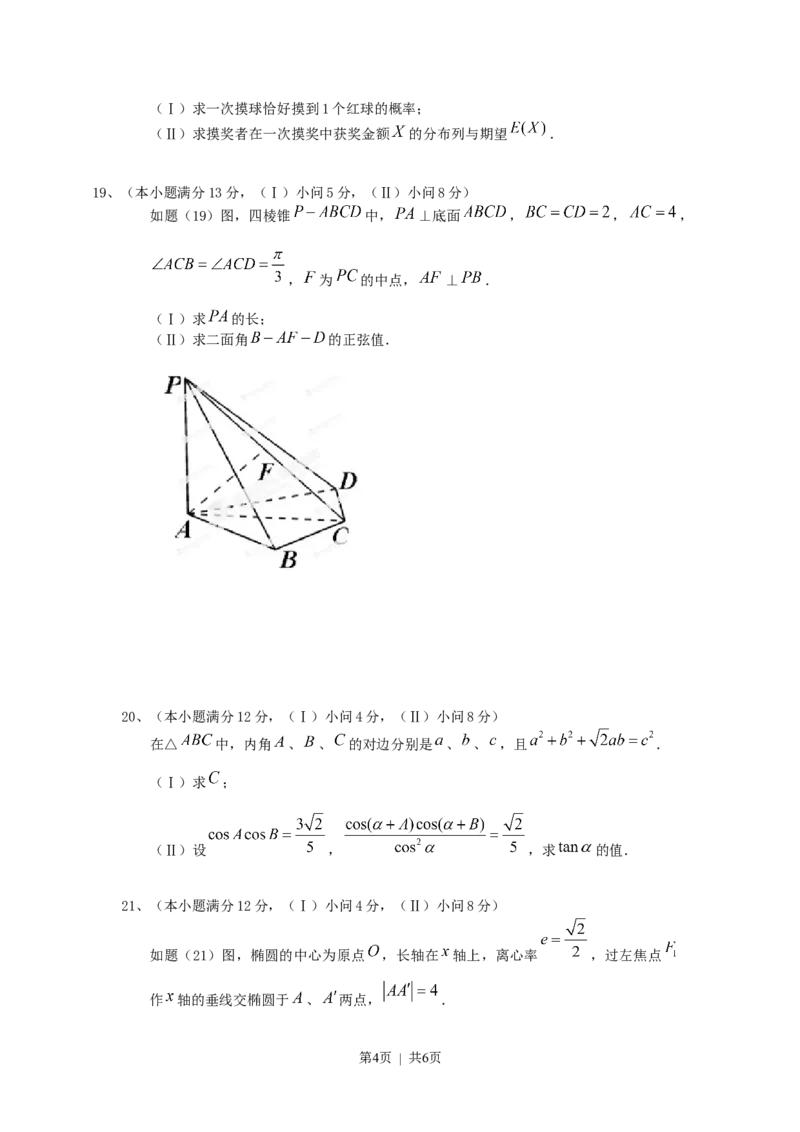
如题(19)图,四棱锥 中, ⊥底面 , , ,
, 为 的中点, ⊥ .
(Ⅰ)求 的长;
(Ⅱ)求二面角 的正弦值.zhangwlx
20、(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)
在△ 中,内角 、 、 的对边分别是 、 、 ,且 .
(Ⅰ)求 ;
(Ⅱ)设 , ,求 的值.
21、(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)zhangwlx
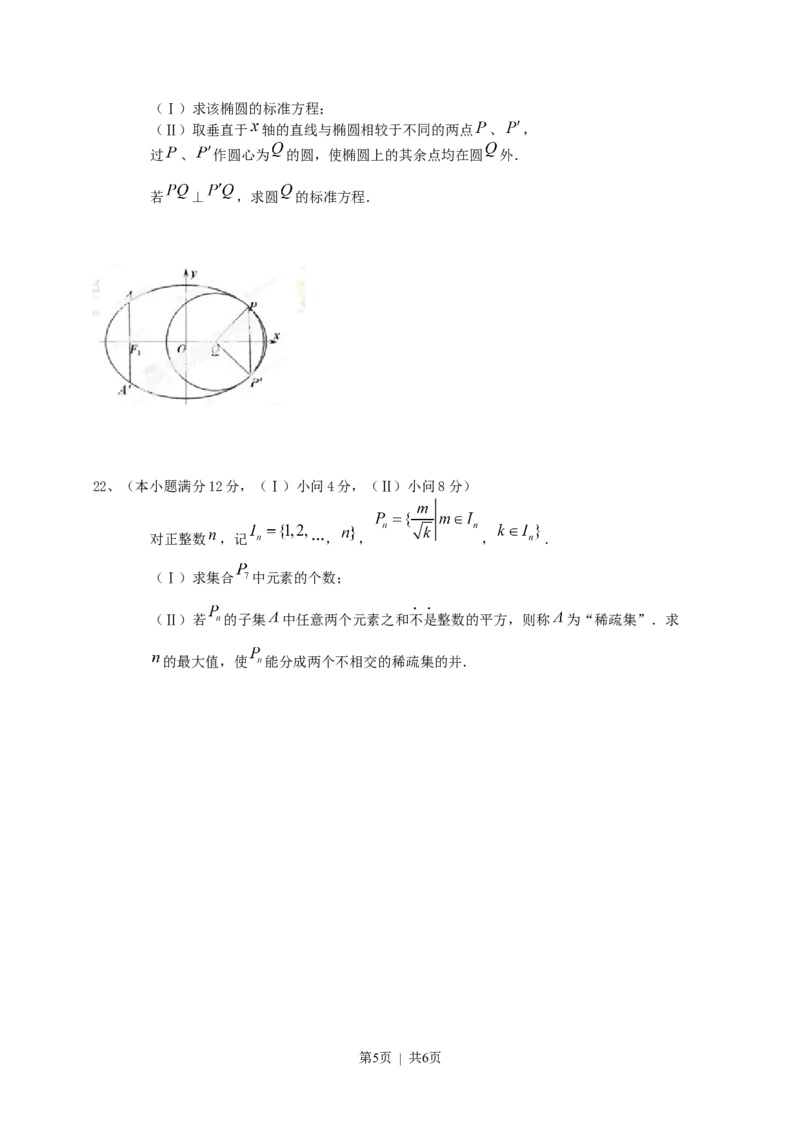
如题(21)图,椭圆的中心为原点 ,长轴在 轴上,离心率 ,过左焦点
作 轴的垂线交椭圆于 、 两点, .
第4页 | 共6页(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取垂直于 轴的直线与椭圆相较于不同的两点 、 ,
过 、 作圆心为 的圆,使椭圆上的其余点均在圆 外.
若 ⊥ ,求圆 的标准方程.
22、(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)
对正整数 ,记 …, , , .
(Ⅰ)求集合 中元素的个数;
(Ⅱ)若 的子集 中任意两个元素之和不是整数的平方,则称 为“稀疏集”.求
的最大值,使 能分成两个不相交的稀疏集的并.
第5页 | 共6页第6页 | 共6页