文档内容
这8道选择题中,第1-3为基础题,注重基础知识的考查、基本公式的应用,第4-7为数形结合的
问题,基本图像的观察以及基本思想的渗透,其中4、5两题注重培养学生的动手能力,要求学生
自己做出图像,自己分析得到答案,第7题注重空间想象能力的培养,要求学生寻找正方体在旋转
过程中的最值,第8题,与平面几何知识想结合,要求将平面几何问题解析话,降低解题的难度;
总体老说,这9道问题难度相对均衡,无偏题、怪题;
二、填空题考点一览表:
题号 主要考点
9 参数方程
10 不等式选讲
11 几何证明
12 定积分的基本运算
第1页 | 共17页第21题:本题为圆锥曲线问题,试题以此开始,难度和计算量有了较大的提升,第(1)小题以向
第2页 | 共17页本试卷包括选择题、填空题和解答题三部分,共 5 页,时量 120 分钟,满分 150 分。
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.复数z =i
g
1+ii为虚数单位 在复平面上对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.某学校有男、女学生各500名.为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟
从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是( )
A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法
3.在锐角中DABC,角A,B所对的边长分别为a,b.若2asinB= 3b,则角A等于( )
p p p p
A. B. C. D.
12 6 4 3
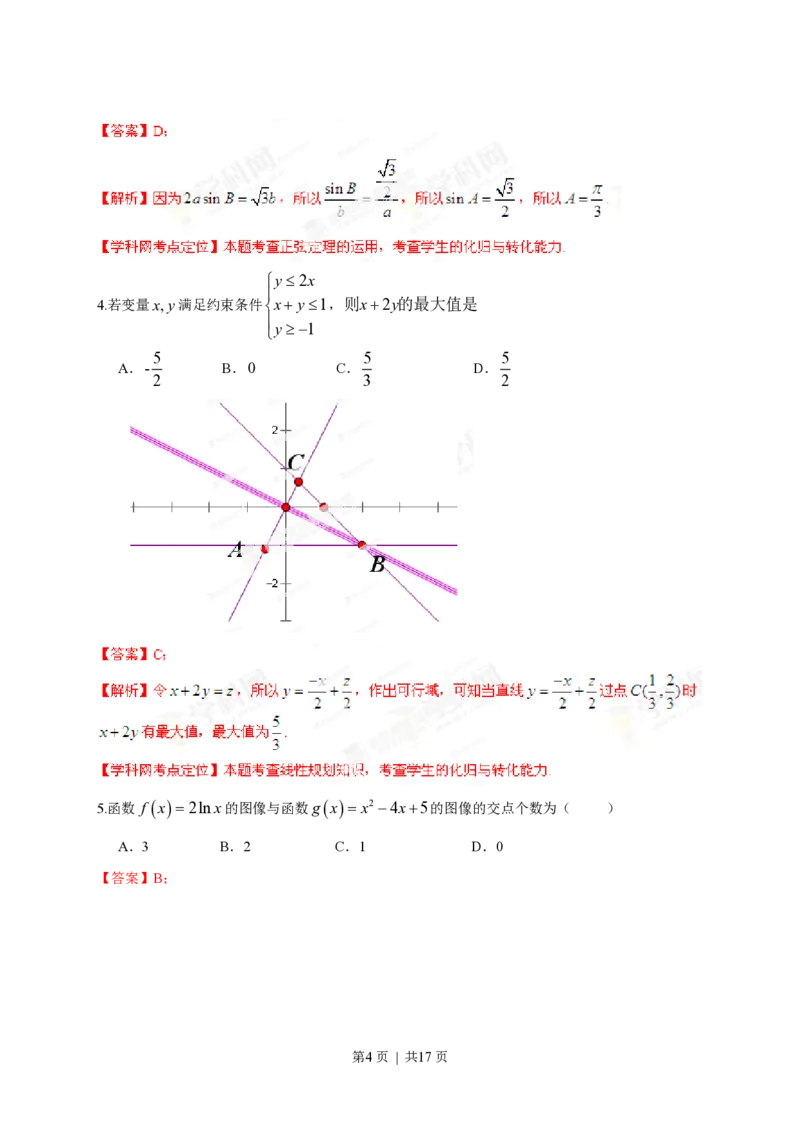
第3页 | 共17页ìy£2x
ï
4.若变量x,y满足约束条件íx+ y£1,则x+2y的最大值是
ï
y³-1
î
5 5 5
A.- B.0 C. D.
2 3 2
5.函数 f x=2lnx的图像与函数gx= x2 -4x+5的图像的交点个数为( )
A.3 B.2 C.1 D.0
【答案】B;
第4页 | 共17页6. 已知a,b是单位向量,a g b=0.若向量c满足 c-a-b =1,则c的取值范围是( )
A.é 2-1,, 2+1ù B.é 2-1,, 2+2ù
ë û ë û
C.é1,, 2+1ù D.é1,, 2+2ù
ë û ë û
7.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能
等于( )
2-1 2+1
A.1 B. 2 C. D.
2 2
【答案】C;
【解析】正方体的正视图面积应当介意1与 2 之间,故C不正确.
【学科网考点定位】本题考查三视图,考查学生的空间想象能力.
8.在等腰三角形ABC中,AB=AC =4,点P是边AB上异于A,B的一点,光线从点P出发,经
BC,CA发射后又回到原点P(如图1).若光线QR经过DABC的中心,则AP等于( )
第5页 | 共17页A.2 B.1
8 4
C. D.
3 3
二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分.
(一)选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题计分)
ìx=t, ìx=3cosj,
l:í (t为参数)过椭圆C:í
9.在平面直角坐标系xoy中,若 îy =t-a îy =2sinj
(j为参数)的右顶点,则常数a的值为 .
10.已知a,b,cÎ,a+2b+3c=6,则a2 +4b2 +9c2的最小值为 .
【答案】12
【解析】 a2 +4b2 +9c2 (12 +12 +12)³(a+2b+3c)2,所以a2 +4b2 +9c2 ³12.
【学科网考点定位】本题考查柯西不等式的使用,考查学生的化归与转化能力.
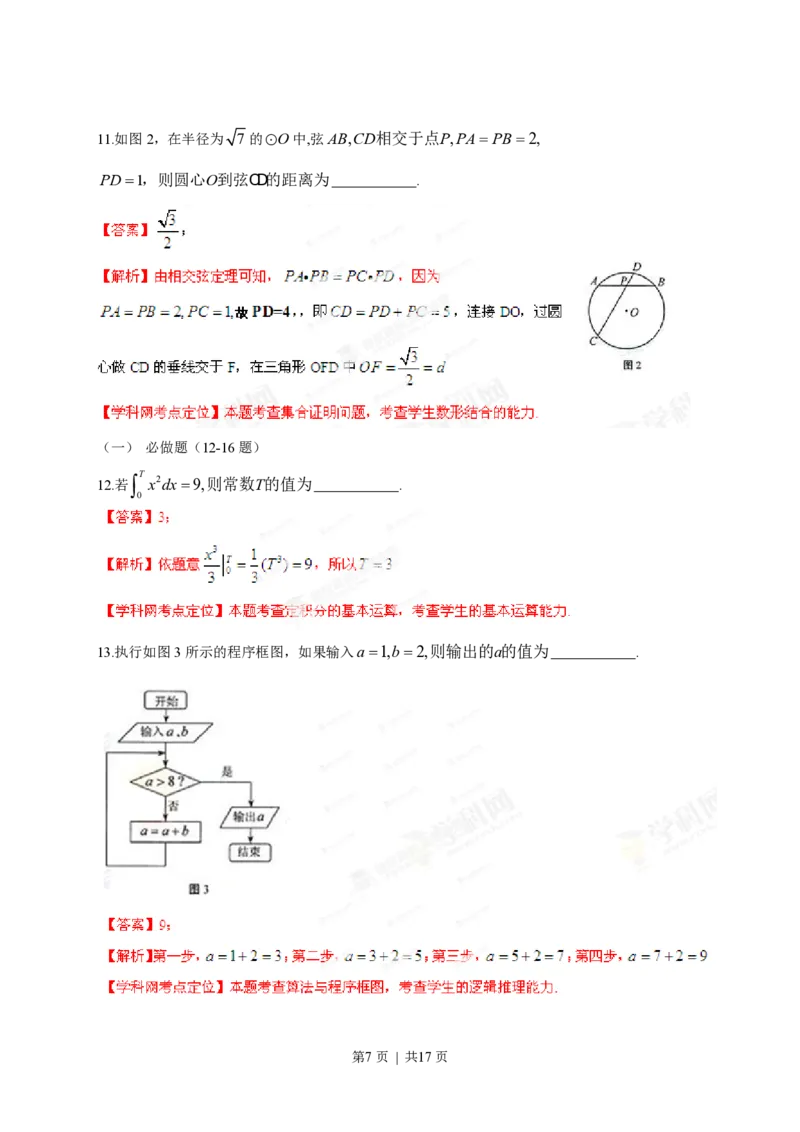
第6页 | 共17页11.如图2,在半径为 7 的 O中,弦AB,CD相交于点P,PA= PB=2,
e
PD=1,则圆心O到弦CD的距离为 .
(一) 必做题(12-16题)
T
12.若ò x2dx=9,则常数T的值为 .
0
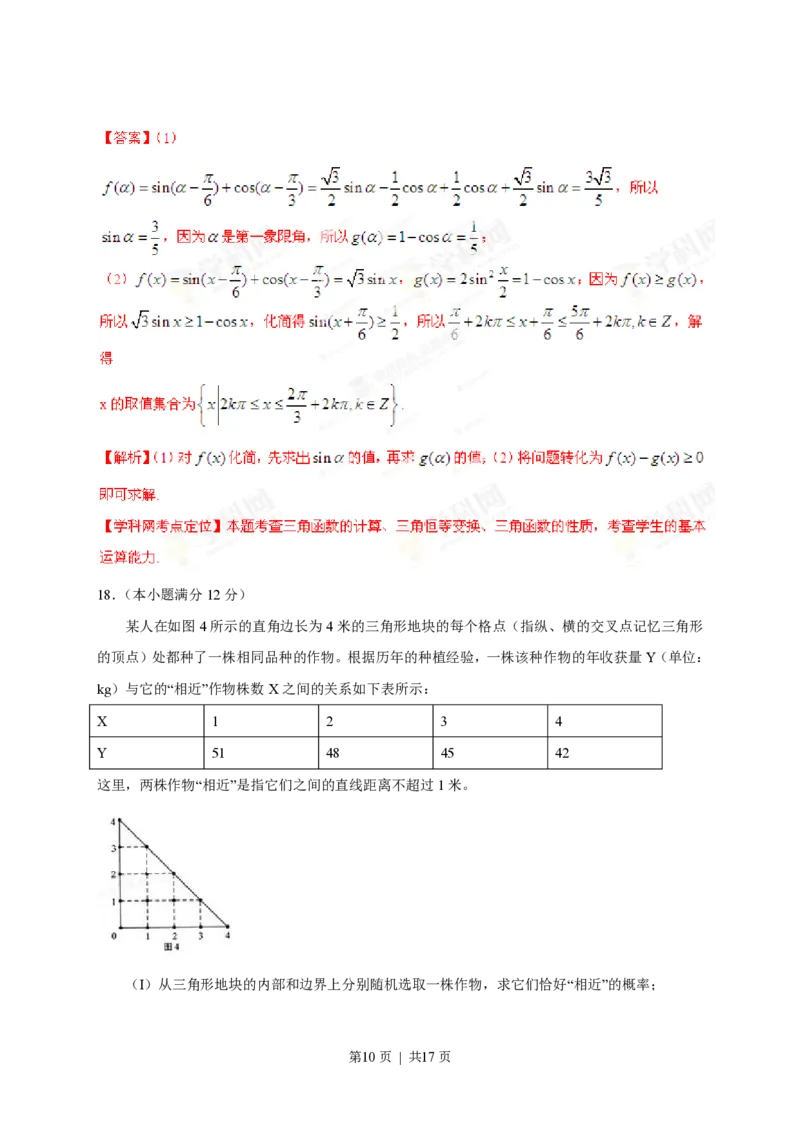
13.执行如图3所示的程序框图,如果输入a =1,b=2,则输出的a的值为 .
第7页 | 共17页x2 y2
14.设F,F 是双曲线C: - =1(a>0,b>0)的两个焦点,P是C上一点,若 PF + PF =6a,
1 2 a2 b2 1 2
且DPFF 的最小内角为30o,则C的离心率为___。
1 2
1
15.设S 为数列a 的前n项和,S =(-1)na - ,nÎN*,则
n n n n 2n
(1)a =_____;
3
(2)S +S +×××+S =___________。
1 2 100
1 1 1
【答案】- ; ( -1).
16 3 2100
1 1 1 1
【解析】(1)令n=1,a =- ;S =a - ,S =-a - ,两式对减得到a =- ;
1 4 4 4 16 3 3 8 3 16
16.设函数 f(x)=ax +bx -cx,其中c>a>0,c>b>0.
(1)记集合M =(a,b,c) a,b,c不能构成一个三角形的三条边长,且a=b,则(a,b,c)ÎM 所
对应的 f(x)的零点的取值集合为____。
(2)若a,b,c是DABC的三条边长,则下列结论正确的是 .(写出所有正确结论
第8页 | 共17页的序号)
①"xÎ-¥,1, f x>0;
②$xÎR,使xax,bx,cx不能构成一个三角形的三条边长;
③若DABC为钝角三角形,则$xÎ1,2,使f x=0.
故③ 正确
【学科网考点定位】本题考查函数的性质,考查学生的化归与转化能力.
本解析为学科网名师解析团队原创,授权学科网独家使用,如有盗用,依法追责!
三、解答题:本大题共 6 小题,共 75 分。解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
p p x
已知函数 f(x)=sin(x- )+cos(x- ).g(x)=2sin2 。
6 3 2
3 3
(I)若a是第一象限角,且 f(a)= 。求g(a)的值;
5
(II)求使 f(x)³ g(x)成立的x的取值集合。
第9页 | 共17页18.(本小题满分12分)
某人在如图4所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形
的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收获量Y(单位:
kg)与它的“相近”作物株数X之间的关系如下表所示:
X 1 2 3 4
Y 51 48 45 42
这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(I)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
第10页 | 共17页(II)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望。
所求分布列为
X 51 48 45 43
2 4 2 1
P
15 15 5 5
故所求期望E(Y)=46
19.(本小题满分12分)
如图5,在直棱柱
ABCD-ABC D中,AD//BC,ÐBAD=90o,AC ^ BD,BC =1,AD= AA =3.
1 1 1 1
1
(I)证明:AC ^ BD;
1
(II)求直线BC与平面ACD 所成角的正弦值。
1 1 1
第11页 | 共17页r
所以n=(1,- 3, 3)为平面ACD 的一个法向量;因为B ( 3,0,3),C ( 3,1,3),所以
1 1 1
20.(本小题满分13分)
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径成为M到N的一
条“L路径”。如图6所示的路径MM M M N与路径MN N 都是M到N的“L路径”。某地有三个
1 2 3 1
新建的居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处。现计划在x轴上方区域
(包含x轴)内的某一点P处修建一个文化中心。
第12页 | 共17页(I)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明);
(II)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定
点P的位置,使其到三个居民区的“L路径”长度值和最小。
【答案】(1)点P到居民区A的“L路径”长度最小值为 x-3 + y-20 ,xÎR,yÎ0,+¥ .
(2)依题意,点P到三个居民区的“L路径”长度之和的最小值为点P分别到三个居民区的“L路
径”长度之和(记为d)的最小值;
1、当y³1时,d = x+10 + x-14 +2 y + y-20 ,因为
d (x)= x+10 + x-14 + x-3 ³ x+10 + x-14 当且仅当x=3时等号成立;
1
第13页 | 共17页21.(本小题满分13分)
过抛物线E:x2 =2py(p >0)的焦点F作斜率分别为k ,k 的两条不同的直线l ,l ,且
1 2 1 2
k +k =2,l与E相交于点A,B,l 与E相交于点C,D。以AB,CD为直径的圆M,圆N
1 2 1 2
(M,N为圆心)的公共弦所在的直线记为l 。
uuuur uuur
(I)若k
1
>0,k
2
>0,证明;FM
g
FN <2P2;
7 5
(II)若点M到直线l 的距离的最小值为 ,求抛物线E的方程。
5
p p
【答案】(1)依题意,抛物线E的交点为F(0, ),直线l 的方程为y =k x+ ,
2 1 1 2
ì p
ïy =k x+
由í 1 2 得x2 -2pk x- p2 =0,设A、B两点的坐标分别为(x ,y ),(x ,y ),则x ,x 是
1 1 1 2 2 1 2
ï îx2 =2py
第14页 | 共17页22.(本小题满分13分)
x - a
已知a > 0 ,函数 f (x) = 。
x + 2a
(I);记 f (x)在 区 间 0,4上 的 最 大 值 为 g( a) , 求g(a)的表达式;
(II)是否存在a,使函数y = f(x)在区间0,4内的图像上存在两点,在该两点处的切线
相互垂直?若存在,求a的取值范围;若不存在,请说明理由。
第15页 | 共17页第16页 | 共17页第17页 | 共17页