2023届福建省漳州市高三上学期第一次教学质量检测数学试题(1)_2023年8月_028月合集_2023届福建省漳州市高三上学期第一次教学质量检测

准考证号 姓名 (在此卷上答题无效) 福建省漳州市 届高三毕业班第一次教学质量检测 ２０２３ 数学试题 本试卷 共 页 考试时间 分钟 满分 分 : ６ : １２０ : １５０ 考生注意: 答题前 考生务必在试题卷 答题卡规定的地方填写自己的准考证号 姓名 考生 １􀆰 ꎬ 、 、 ꎮ 要认真核对答题卡上粘贴的条形码的 准考证号 姓名 与考生本人准考证号 姓名是否 “ 、 ” 、 一致 ꎮ 回答选择题时 选出每小题答案后 用 铅笔把答题卡上对应题目的答案标号涂 ２􀆰 ꎬ ꎬ ２Ｂ 黑 如需改动 用橡皮擦干净后 再选涂其它答案标号 回答非选择题时 用 黑色 ꎮ ꎬ ꎬ ꎮ ꎬ ０􀆰５ｍｍ 签字笔将答案写在答题卡上 写在本试卷上无效 ꎮ ꎮ 考试结束 考生必须将试题卷和答题卡一并交回 ３􀆰 ꎬ ꎮ 一、 单项选择题: 本大题共 小题ꎬ 每小题 分ꎬ 共 分ꎬ 在每小题给出的四个选项中ꎬ ８ ５ ４０ 只有一项是符合题目要求的ꎮ . 已知集合Ａ ＝{ } Ｂ ＝{ } 全集Ｕ ＝Ａ Ｂ 则集合 Ａ Ｂ 中的元 １ ４ꎬ ５ꎬ ６ꎬ ７ ꎬ ６ꎬ ７ꎬ ８ ꎬ ∪ ꎬ Ｕ( ∩ ) 素个数为 Ａ. １ Ｂ. ２ Ｃ. ３ Ｄ. ４ . 若复数ｚ满足ｚ ＋ ＝ ｚ 为虚数单位 则 ｚ ＝ ２ ｉ 􀅰ｉ(ｉ )ꎬ ２ Ａ. Ｂ. １ Ｃ. ２ Ｄ. ２ ２ . 已知ｐ ｘｙ > ｑ ｘ > ｙ > 则ｐ是ｑ的 ３ : ０ꎬ : ０ꎬ ０ꎬ 充分不必要条件 必要不充分条件 Ａ. Ｂ. 充要条件 既不充分也不必要条件 Ｃ. Ｄ. . 已知→ａ →ｂ →ｃ 均为单位向量 且满足→ａ ＋ →ｂ ＋ →ｃ ＝→ 则 < →ａ － →ｂ →ｃ > ＝ ４ ꎬ ꎬ ꎬ ０ꎬ ꎬ π π π ２π Ａ. Ｂ. Ｃ. Ｄ. ６ ３ ２ ３ . 已知 π － α ＝ ５ 则 α ＝ ５ ｃｏｓ( ) ꎬ ｓｉｎ２ ４ ５ １ － １ － ２ － ３ Ａ. Ｂ. Ｃ. Ｄ. ５ ５ ５ ５ 数学第一次教学质量检测 第 １页 (共６页). 已知 ａ ｘ － １ ５ ａ为常数 的展开式中所有项系数的和与二项式系数的和相等 则该展 ６ ( ３ｘ) ( ) ꎬ 开式中的常数项为 － － Ａ. ９０ Ｂ. １０ Ｃ. １０ Ｄ. ９０ . 设ａ ＝ １ ｂ ＝ １ ｃ ＝ １ 则 ７ ５ｓｉｎ ꎬ ｃｏｓ ꎬ １０ｓｉｎ ꎬ ５ １０ １０ ｃ < ｂ < ａ ｂ < ａ < ｃ ａ < ｃ < ｂ ａ < ｂ < ｃ Ａ. Ｂ. Ｃ. Ｄ. . 已知Ａ Ｂ分别为ｘ轴 ｙ轴上的动点 若以ＡＢ为直径的圆与直线 ｘ ＋ ｙ － ＝ 相切 ８ ꎬ ꎬ ꎬ ２ ４ ０ ꎬ 则该圆面积的最小值为 π ２π ４π Ａ. Ｂ. Ｃ. Ｄ. π ５ ５ ５ 二、 多项选择题: 本大题共 小题ꎬ 每小题 分ꎬ 共 分ꎬ 在每小题给出的四个选项中ꎬ 有 ４ ５ ２０ 多个选项符合题目要求ꎬ 全部选对的得 分ꎬ 选对但不全的得 分ꎬ 有选错的得 分ꎮ ５ ２ ０ æ ö . 已知函数ｆ ｘ ＝ ç ｘ － π÷ 则 ９ ( ) ｔａｎè２ ø ꎬ ３ ｆ ｘ 的最小正周期是π Ａ. ( ) ２ æ ö ｆ ｘ 的图象关于点ç５π ÷ 中心对称 Ｂ. ( ) è ꎬ ０ø １２ ｆ(ｘ) 在( ) 上有三个零点 Ｃ. ０ꎬ π ｆ(ｘ) 的图象可以由ｇ(ｘ) ＝ ｘ的图象上的所有点向右平移π 个单位长度得到 Ｄ. ｔａｎ２ ３ ｙ２ . 已知椭圆ｘ２ ＋ ＝ 的上下焦点分别为Ｆ Ｆ 左右顶点分别为Ａ Ａ Ｐ是该椭圆上 １０ １ １ꎬ ２ꎬ １ꎬ ２ꎬ ２ 的动点 则下列结论正确的是 ꎬ 该椭圆的长轴长为 Ａ. ２ 使ΔＰＦ Ｆ 为直角三角形的点Ｐ共有 个 Ｂ. １ ２ ６ ΔＰＦ Ｆ 的面积的最大值为 Ｃ. １ ２ １ 若点Ｐ是异于Ａ Ａ 的点 则直线ＰＡ 与ＰＡ 的斜率的乘积等于 － Ｄ. １、 ２ ꎬ １ ２ ２ 数学第一次教学质量检测 第 ２页 (共６页). 如图 在多面体 ＥＦＧ － ＡＢＣＤ 中 四边形 ＡＢＣＤ ＣＦＧＤ ＡＤＧＥ 均是边长为 的正方 １１ ꎬ ꎬ ꎬ ꎬ １ 形 点Ｈ在棱ＥＦ上 则 G F ꎬ ꎬ H 该几何体的体积为２ E Ａ. ３ 点Ｄ在平面ＢＥＦ内的射影为ΔＢＥＦ的垂心 Ｂ. D C ＧＨ ＋ ＢＨ的最小值为 Ｃ. ３ 存在点Ｈ 使得ＤＨ ＢＦ A B Ｄ. ꎬ ⊥ . 大衍数列来源于 乾坤谱 中对易传 大衍之数五十 的推论 主要用于解释中国传统文 １２ « » “ ” ꎬ 化中的太极衍生原理 数列中的每一项都代表太极衍生过程. 已知大衍数列{ａ } 满足 ꎬ ｎ {ａ ＋ ｎ ＋ ｎ为奇数 ｎ １( ) ａ ＝ ａ ＝ 则 １ ０ꎬ ｎ＋ １ ａ ＋ ｎ ｎ为偶数 ꎬ ｎ ( ) ａ ＝ ａ ＝ ａ ＋ ｎ ＋ Ａ. ４ ６ Ｂ. ｎ＋ ２ ｎ ２( １) ì ï ｎ２ － １ ｎ为奇数 ï ( ) ï ２ ａ ＝ í 数列{ － ｎａ }的前 ｎ项和为ｎ ｎ ＋ Ｃ. ｎ ï Ｄ. ( １) ｎ ２ ( １) ｎ２ ïï ｎ为偶数 î ( ) ２ 三、 填空题: 本题共 小题ꎬ 每小题 分ꎬ 共 分ꎮ ４ ５ ２０ . 树人中学举办以 喜迎二十大 永远跟党走 奋进新征程 为主题的演讲比赛 其中 人 １３ “ 、 、 ” ꎬ ９ 比赛的成绩为 单位 分 则这 人成绩的第 : ８５ꎬ ８６ꎬ ８８ꎬ ８８ꎬ ８９ꎬ ９０ꎬ ９２ꎬ ９４ꎬ ９８( : )ꎬ ９ 百分位数是 . ８０ . 已知直线ｘ ＋ ｙ ＋ ａ ＝ 是曲线ｘｙ － ＝ 的切线 则ａ ＝ . １４ ０ １ ０ ꎬ ｘ２ . 已知双曲线 － ｙ２ ＝ ａ > 的左右焦点分别为Ｆ Ｆ 过Ｆ 的直线与双曲线的左右 １５ ａ２ １( ０) １ꎬ ２ꎬ １ 两支分别交于 Ａ Ｂ 两点. 若 ＡＦ ＝ ＢＦ 且 ＡＢ ＝ 则该双曲线的离心率为 ꎬ ２ ２ ꎬ ８ꎬ . . 已知正四棱锥的各顶点都在同一个球面上. 若该正四棱锥的体积为６４ 则该球的表面积 １６ ꎬ ３ 的最小值为 . 数学第一次教学质量检测 第 ３页 (共６页)四、 解答题: 本大题共 小题ꎬ 共 分ꎬ 解答应写出文字说明、 证明过程或演算步骤ꎮ ６ ７０ . 分 １７ (１０ ) 已知等比数列{ａ ｎ }的各项均为正数 ꎬ 且 ２ ａ １ ＋ ３ ａ ２ ＝ １ꎬ ａ２ ３ ＝ ９ ａ ２ ａ ６ . 求{ａ }的通项公式 (１) ｎ ꎻ { } 设ｂ ＝ ａ ＋ ａ ＋ ＋ ａ 求数列 １ 的前ｎ项和Ｔ . (２) ｎ ｌｏｇ３ １ ｌｏｇ３ ２ 􀆺 ｌｏｇ３ ｎꎬ ｂ ｎ ｎ . 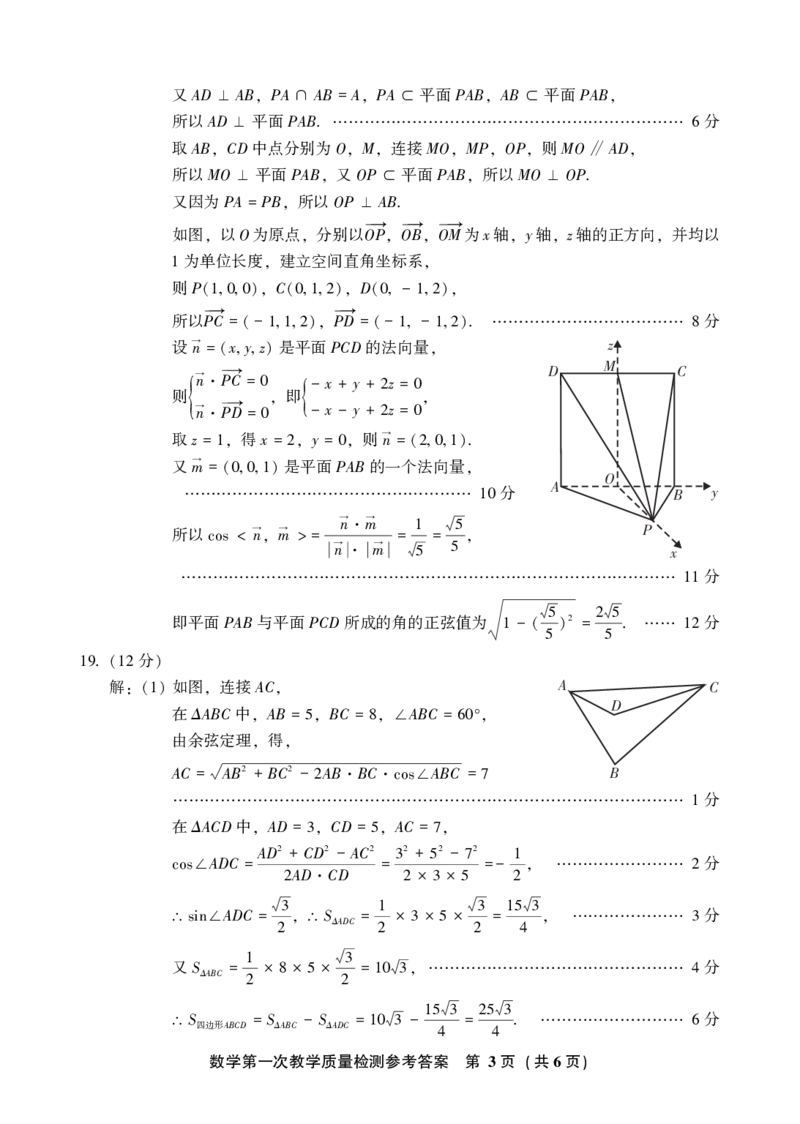分 １８ (１２ ) 如图 在四棱锥Ｐ－ＡＢＣＤ中 四边形ＡＢＣＤ是边长为 的正方形 ＡＰ ＢＰ ＡＰ＝ＢＰ ꎬ ꎬ ２ ꎬ ⊥ ꎬ ꎬ ＰＤ ＝ . 记平面ＰＡＢ与平面ＰＣＤ的交线为ｌ. ６ 证明 ＡＢ ｌ D C (１) : ∥ ꎻ 求平面ＰＡＢ与平面ＰＣＤ所成的角的正弦值. (２) A B P 数学第一次教学质量检测 第 ４页 (共６页). 分 １９ (１２ ) 密铺 即平面图形的镶嵌 指用形状 大小完全相同的平面图形进行拼接 使彼此之间 ꎬ ꎬ 、 ꎬ 不留空隙 不重叠地铺成一片. 皇冠图形 图 是一个密铺图形 它由四个完全相同的平面 、 ( １) ꎬ 凹四边形组成 为测皇冠图形的面积 测得在平面凹四边形 ＡＢＣＤ 图 中 ＡＢ ＝ 􀆰 ꎬ ( ２) ꎬ ５ꎬ ＢＣ ＝ ＡＢＣ ＝ °. ８ꎬ ∠ ６０ 若ＣＤ ＝ ＡＤ ＝ 求平面凹四边形ＡＢＣＤ的面积 (１) ５ꎬ ３ꎬ ꎻ 若 ＡＤＣ ＝ ° 求平面凹四边形ＡＢＣＤ的面积的最小值. (２) ∠ １２０ ꎬ A C D B !1 !2 . 分 ２０ (１２ ) 漳州某地准备建造一个以水仙花为主题的公园. 在建园期间 甲 乙 丙三个工作队负 ꎬ 、 、 责采摘及雕刻水仙花球茎. 雕刻时会损坏部分水仙花球茎 假设水仙花球茎损坏后便不能使 ꎬ 用 无损坏的全部使用 已知甲 乙 丙工作队所采摘的水仙花球茎分别占采摘总量的 ꎬ ꎮ 、 、 ％ ％ ％ 甲 乙 丙工作队采摘的水仙花球茎的使用率分别为 ２５ ꎬ ３５ ꎬ ４０ ꎬ 、 、 ０􀆰８ꎬ ０􀆰６ꎬ ０􀆰７５ 能使用的水仙花球茎数 水仙花球茎的使用率 ＝ . ( 采摘的水仙花球茎总数) 从采摘的水仙花球茎中有放回地随机抽取三次 每次抽取一颗 记甲工作队采摘的 (１) ꎬ ꎬ 水仙花球茎被抽取到的次数为ξ 求随机变量ξ的分布列及期望 ꎬ ꎻ 已知采摘的某颗水仙花球茎经雕刻后能使用 求它是由丙工作队所采摘的概率. (２) ꎬ 数学第一次教学质量检测 第 ５页 (共６页)分 ２１􀆰(１２ ) 已知抛物线Ｃ ｙ２ ＝ ｘ 直线ｌ过点Ｐ( ) . : ４ ꎬ ０ꎬ １ 若ｌ与Ｃ有且只有一个公共点 求直线ｌ的方程 (１) ꎬ ꎻ ＡＰ ＡＱ 若ｌ与Ｃ交于Ａ Ｂ两点 点Ｑ在线段ＡＢ上 且 ＝ 求点Ｑ的轨迹方程. (２) ꎬ ꎬ ꎬ ＰＢ ＱＢ ꎬ . 分 ２２ (１２ ) 已知函数ｆ ｘ ＝ (ｘ ＋ ) (ｘ ＋ ) － λｘ. ( ) １ ｌｎ １ 当ｘ 时 ｆ(ｘ) 求λ的最大值 (１) ≥０ ꎬ ≥０ꎬ ꎻ 设ｎ Ｎ∗ 证明 － １ ＋ １ － １ ＋ ＋ １ － １ < . (２) ∈ ꎬ : １ 􀆺 ｎ － ｎ ｌｎ２ ２ ３ ４ ２ １ ２ 数学第一次教学质量检测 第 ６页 (共６页)福建省漳州市 届高三毕业班第一次教学质量检测 ２０２３ 数学参考答案及评分细则 评分说明: 本解答给出了一种或几种解法供参考ꎬ 如果考生的解法与本解答不同ꎬ 可根据试题 １. 的主要考查内容比照评分标准制定相应的评分细则ꎮ 对计算题ꎬ 当考生的解答在某一步出现错误时ꎬ 如果后继部分的解答未改变该题的 ２. 内容和难度ꎬ 可视影响的程度决定后继部分的给分ꎬ 但不得超过该部分正确解答应给分数的 一半ꎻ 如果后继部分的解答有较严重的错误ꎬ 就不再给分ꎮ 解答右端所注分数ꎬ 表示考生正确做到这一步应得的累加分数ꎮ ３. 只给整数分数ꎮ 选择题和填空题不给中间分ꎮ ４. 一、 单项选择题: 本大题共 小题ꎬ 每小题 分ꎬ 共 分ꎬ 在每小题给出的四个选项中ꎬ ８ ５ ４０ 只有一项是符合题目要求的ꎮ １ ２ ３ ４ ５ ６ ７ ８ Ｃ Ａ Ｂ Ｃ Ｄ Ａ Ｄ Ｃ 二、 多项选择题: 本大题共 小题ꎬ 每小题 分ꎬ 共 分ꎬ 在每小题给出的四个选项中ꎬ ４ ５ ２０ 有多个选项符合题目要求ꎬ 全部选对的得 分ꎬ 选对但不全的得 分ꎬ 有选错的得 ５ ２ ０ 分ꎮ ９ １０ １１ １２ ＡＢ ＢＣＤ ＢＤ ＢＣＤ 三、 填空题: 本题共 小题ꎬ 每小题 分ꎬ 共 分ꎮ ４ ５ ２０ . . ± . ５ . １３ ９４ １４ ２ １５ １６ ３６π ２ 四、 解答题: 本大题共 小题ꎬ 共 分ꎬ 解答应写出文字说明、 证明过程或演算步骤ꎮ ６ ７０ . 分 １７ (１０ ) ａ２ 解 : (１) 设{ａ ｎ }的公比为ｑ ꎬ 则ａ２ ３ ＝ ９ ａ ２ ａ ６ ＝ ９ ａ２ ４ꎬ 所以ｑ２ ＝ ａ ４ ２ ＝ １. 􀆺􀆺􀆺􀆺􀆺 １ 分 ９ ３ 又ａ > 所以ｑ > 所以ｑ ＝ １. 分 ｎ ０ꎬ ０ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ２ ３ 由 ａ ＋ ａ ＝ 得 ａ ＋ ａ ｑ ＝ 所以ａ ＝ １ 分 ２ １ ３ ２ １ꎬ ２ １ ３ １ １ꎬ １ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ４ ３ 所以{ａ }是首项为１ 公比为１ 的等比数列 所以{ａ }的通项公式为ａ ＝ １. ｎ ꎬ ꎬ ｎ ｎ ｎ ３ ３ ３ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ 数学第一次教学质量检测参考答案 第 １页 (共６页)因为ｂ ＝ ａ ＋ ａ ＋ ＋ ａ ＝ ａ ａ ａ (２) ｎ ｌｏｇ３ １ ｌｏｇ３ ２ 􀆺 ｌｏｇ３ ｎ ｌｏｇ３( １ ２􀆺 ｎ) ｎ ｎ ＋ ＝ － (１ ＋ ２ ＋ 􀆺 ＋ｎ ) ＝－ ＋ ＋ ＋ ｎ ＝－ ( １) 分 ｌｏｇ３３ (１ ２ 􀆺 ) ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ ２ 所以１ ＝－ ２ ＝－ １ － １ . 分 ｂ ｎ ｎ ＋ ２( ｎ ｎ ＋ ) 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ８ ｎ ( １) １ 所以Ｔ ＝ １ ＋ １ ＋ ＋ １ ｎ ｂ ｂ 􀆺 ｂ ｎ １ ２ éæ ö æ ö æ ö ù ｎ ＝－ ê êç － １ ÷ ＋ ç １ － １ ÷ ＋ ＋ ç １ － １ ÷ ú ú ＝－ ２ . ２ëè１ ø è ø 􀆺 è ｎ ｎ ＋ ø û ｎ ＋ ２ ２ ３ １ １ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ . 分 １８ (１２ ) 解 因为ＡＢ ＣＤ ＣＤ 平面ＰＣＤ ＡＢ 平面ＰＣＤ : (１) ∥ ꎬ ⊂ ꎬ ⊄ ꎬ 所以ＡＢ 平面ＰＣＤ. 分 ∥ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ２ 又ＡＢ 平面ＰＡＢ 平面ＰＡＢ 平面ＰＣＤ ＝ ｌ 所以ＡＢ ｌ. 分 ⊂ ꎬ ∩ ꎬ ∥ 􀆺􀆺􀆺􀆺 ４ 解法一 因为ＡＰ ＢＰ 所以ＰＡ２ ＋ ＰＢ２ ＝ ＡＢ２ ＝ 又ＰＡ ＝ ＰＢ (２) : ⊥ ꎬ ４ꎬ ꎬ 所以ＰＡ ＝ ＰＢ ＝ ２ꎬ 又ＰＤ ＝ 所以ＰＡ２ ＋ ＡＤ２ ＝ ＰＤ２ 所以ＡＤ ＰＡ ６ꎬ ꎬ ⊥ ꎬ 又ＡＤ ＡＢ ＰＡ ＡＢ ＝ Ａ ＰＡ 平面ＰＡＢ ＡＢ 平面ＰＡＢ ⊥ ꎬ ∩ ꎬ ⊂ ꎬ ⊂ ꎬ 所以ＡＤ 平面ＰＡＢ. 分 D M C ⊥ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ６ 取ＡＢ ＣＤ中点分别为Ｏ Ｍ 连接ＭＯ ＭＰ ＯＰ ꎬ ꎬ ꎬ ꎬ ꎬ ꎬ 则ＭＯ ＡＤ 所以ＭＯ 平面ＰＡＢ ∥ ꎬ ⊥ ꎬ 又ＯＰ 平面ＰＡＢ 所以ＭＯ ＯＰ. ⊂ ꎬ ⊥ 因为ＰＡ ＝ ＰＢ 所以ＯＰ ＡＢ. O ꎬ ⊥ A B 又ΔＰＡＤ ΔＰＢＣ 所以ＰＣ ＝ ＰＤ 所以ＭＰ ＣＤ. ≌ ꎬ ꎬ ⊥ 又ＡＢ ｌ ＣＤ ｌ 所以ＯＰ ｌ ＭＰ ｌ P ∥ ꎬ ∥ ꎬ ⊥ ꎬ ⊥ ꎬ 所以 ＭＰＯ为平面ＰＡＢ与平面ＰＣＤ所成的角. 分 ∠ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ 在 ΔＰＯＭ中 ＯＰ ＝ １ＡＢ ＝ ＭＯ ＝ Ｒｔ ꎬ １ꎬ ２ꎬ ２ ＭＯ 所以ＰＭ ＝ ＭＰＯ ＝ ＝ ２ ５ ５ꎬ ｓｉｎ∠ ＰＭ ꎬ ５ 即平面ＰＡＢ与平面ＰＣＤ所成的角的正弦值为２ ５. 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ５ 解法二 因为ＡＰ ＢＰ 所以ＰＡ２ ＋ ＰＢ２ ＝ ＡＢ２ ＝ 又ＰＡ ＝ ＰＢ : ⊥ ꎬ ４ꎬ ꎬ 所以ＰＡ ＝ ＰＢ ＝ ２ꎬ 又ＰＤ ＝ 所以ＰＡ２ ＋ ＡＤ２ ＝ ＰＤ２ 所以ＡＤ ＰＡ ６ꎬ ꎬ ⊥ ꎬ 数学第一次教学质量检测参考答案 第 ２页 (共６页)又ＡＤ ＡＢ ＰＡ ＡＢ ＝ Ａ ＰＡ 平面ＰＡＢ ＡＢ 平面ＰＡＢ ⊥ ꎬ ∩ ꎬ ⊂ ꎬ ⊂ ꎬ 所以ＡＤ 平面ＰＡＢ. 分 ⊥ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ６ 取ＡＢ ＣＤ中点分别为Ｏ Ｍ 连接ＭＯ ＭＰ ＯＰ 则ＭＯ ＡＤ ꎬ ꎬ ꎬ ꎬ ꎬ ꎬ ∥ ꎬ 所以ＭＯ 平面ＰＡＢ 又ＯＰ 平面ＰＡＢ 所以ＭＯ ＯＰ. ⊥ ꎬ ⊂ ꎬ ⊥ 又因为ＰＡ ＝ ＰＢ 所以ＯＰ ＡＢ. ꎬ ⊥ 如图 以Ｏ为原点 分别以Ｏ→Ｐ Ｏ→Ｂ Ｏ→Ｍ为ｘ轴 ｙ轴 ｚ轴的正方向 并均以 ꎬ ꎬ ꎬ ꎬ ꎬ ꎬ ꎬ 为单位长度 建立空间直角坐标系 １ ꎬ ꎬ 则Ｐ Ｃ Ｄ － (１􀆯０􀆯０)ꎬ (０􀆯１􀆯２)ꎬ (０􀆯 １􀆯２)ꎬ 所以Ｐ→Ｃ ＝ － Ｐ→Ｄ ＝ － － . 分 ( １􀆯１􀆯２)ꎬ ( １􀆯 １􀆯２) 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ８ 设→ｎ ＝ ｘ ｙ ｚ 是平面ＰＣＤ的法向量 z ( 􀆯 􀆯 ) ꎬ D M C { →ｎ Ｐ→Ｃ ＝ {－ ｘ ＋ ｙ ＋ ｚ ＝ 则 􀅰 ０ 即 ２ ０ →ｎ Ｐ→Ｄ ＝ ꎬ － ｘ － ｙ ＋ ｚ ＝ ꎬ 􀅰 ０ ２ ０ 取ｚ ＝ 得ｘ ＝ ｙ ＝ 则→ｎ ＝ . １ꎬ ２ꎬ ０ꎬ (２􀆯０􀆯１) 又ｍ→ ＝ 是平面ＰＡＢ的一个法向量 (０􀆯０􀆯１) ꎬ O A 分 B y 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ →ｎ ｍ→ P 所以 < →ｎ ｍ→ > ＝ 􀅰 ＝ １ ＝ ５ ｃｏｓ ꎬ →ｎ ｍ→ ꎬ x 􀅰 ５ ５ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ 即平面ＰＡＢ与平面ＰＣＤ所成的角的正弦值为 － ５ ２ ＝ ２ ５. 分 １ ( ) 􀆺􀆺 １２ ５ ５ . 分 １９ (１２ ) 解 如图 连接ＡＣ A C : (１) ꎬ ꎬ D 在ΔＡＢＣ中 ＡＢ ＝ ＢＣ ＝ ＡＢＣ ＝ ° ꎬ ５ꎬ ８ꎬ ∠ ６０ ꎬ 由余弦定理 得 ꎬ ꎬ ＡＣ ＝ ＡＢ２ ＋ ＢＣ２ － ＡＢ ＢＣ ＡＢＣ ＝ B ２ 􀅰 􀅰ｃｏｓ∠ ７ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ 在ΔＡＣＤ中 ＡＤ ＝ ＣＤ ＝ ＡＣ ＝ ꎬ ３ꎬ ５ꎬ ７ꎬ ＡＤ２ ＋ ＣＤ２ － ＡＣ２ ２ ＋ ２ － ２ ＡＤＣ ＝ ＝ ３ ５ ７ ＝－ １ 分 ｃｏｓ∠ ＡＤ ＣＤ × × ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ２ ２ 􀅰 ２ ３ ５ ２ ＡＤＣ ＝ ３ Ｓ ＝ １ × × × ３ ＝ １５ ３ 分 ∴ ｓｉｎ∠ ꎬ ∴ ΔＡＤＣ ３ ５ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ３ ２ ２ ２ ４ 又Ｓ ＝ １ × × × ３ ＝ 分 ΔＡＢＣ ８ ５ １０ ３ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ４ ２ ２ Ｓ ＝ Ｓ － Ｓ ＝ － １５ ３ ＝ ２５ ３. 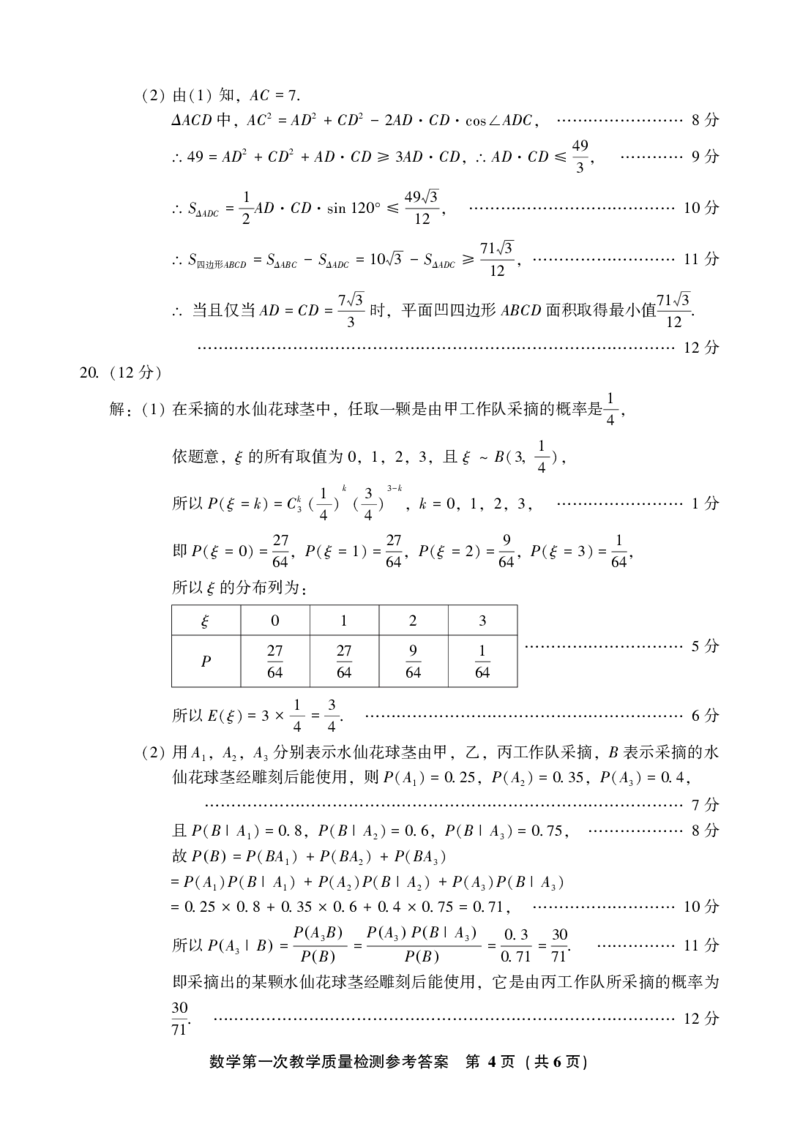分 ∴ 四边形ＡＢＣＤ ΔＡＢＣ ΔＡＤＣ １０ ３ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ６ ４ ４ 数学第一次教学质量检测参考答案 第 ３页 (共６页)由 知 ＡＣ ＝ . (２) (１) ꎬ ７ ΔＡＣＤ中 ＡＣ２ ＝ ＡＤ２ ＋ ＣＤ２ － ＡＤ ＣＤ ＡＤＣ 分 ꎬ ２ 􀅰 􀅰ｃｏｓ∠ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ８ ＝ ＡＤ２ ＋ ＣＤ２ ＋ ＡＤ ＣＤ ＡＤ ＣＤ ＡＤ ＣＤ ４９ 分 ∴ ４９ 􀅰 ≥３ 􀅰 ꎬ ∴ 􀅰 ≤ ꎬ 􀆺􀆺􀆺􀆺 ９ ３ Ｓ ＝ １ＡＤ ＣＤ ° ４９ ３ 分 ∴ ΔＡＤＣ 􀅰 􀅰ｓｉｎ１２０ ≤ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ ２ １２ Ｓ ＝ Ｓ － Ｓ ＝ － Ｓ ７１ ３ 分 ∴ 四边形ＡＢＣＤ ΔＡＢＣ ΔＡＤＣ １０ ３ ΔＡＤＣ ≥ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ １２ 当且仅当ＡＤ ＝ ＣＤ ＝ ７ ３ 时 平面凹四边形ＡＢＣＤ面积取得最小值７１ ３. ∴ ꎬ ３ １２ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ . 分 ２０ (１２ ) 解 在采摘的水仙花球茎中 任取一颗是由甲工作队采摘的概率是１ : (１) ꎬ ꎬ ４ 依题意 ξ 的所有取值为 且ξ ~ Ｂ １ ꎬ ０ꎬ １ꎬ ２ꎬ ３ꎬ (３􀆯 )ꎬ ４ ｋ －ｋ 所以Ｐ ξ ＝ ｋ ＝ Ｃｋ １ ３ ３ ｋ ＝ 分 ( ) ３ ( ) ( ) ꎬ ０ꎬ １ꎬ ２ꎬ ３ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ ４ ４ 即Ｐ ξ ＝ ＝ ２７ Ｐ ξ ＝ ＝ ２７ Ｐ ξ ＝ ＝ ９ Ｐ ξ ＝ ＝ １ ( ０) ꎬ ( １) ꎬ ( ２) ꎬ ( ３) ꎬ ６４ ６４ ６４ ６４ 所以ξ 的分布列为 : ξ ０ １ ２ ３ 分 Ｐ ２７ ２７ ９ １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ ６４ ６４ ６４ ６４ 所以Ｅ ξ ＝ × １ ＝ ３. 分 ( ) ３ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ６ ４ ４ 用Ａ Ａ Ａ 分别表示水仙花球茎由甲 乙 丙工作队采摘 Ｂ表示采摘的水 (２) １ꎬ ２ꎬ ３ ꎬ ꎬ ꎬ 仙花球茎经雕刻后能使用 则Ｐ Ａ ＝ Ｐ Ａ ＝ Ｐ Ａ ＝ ꎬ ( １) ０􀆰２５ꎬ ( ２) ０􀆰３５ꎬ ( ３) ０􀆰４ꎬ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ 且Ｐ Ｂ｜ Ａ ＝ Ｐ Ｂ｜ Ａ ＝ Ｐ Ｂ｜ Ａ ＝ 分 ( １) ０􀆰８ꎬ ( ２) ０􀆰６ꎬ ( ３) ０􀆰７５ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺 ８ 故Ｐ(Ｂ) ＝ Ｐ ＢＡ ＋ Ｐ ＢＡ ＋ Ｐ ＢＡ ( １) ( ２) ( ３) ＝ Ｐ Ａ Ｐ Ｂ｜ Ａ ＋ Ｐ Ａ Ｐ Ｂ｜ Ａ ＋ Ｐ Ａ Ｐ Ｂ｜ Ａ ( １) ( １) ( ２) ( ２) ( ３) ( ３) ＝ × ＋ × ＋ × ＝ 分 ０􀆰２５ ０􀆰８ ０􀆰３５ ０􀆰６ ０􀆰４ ０􀆰７５ ０􀆰７１ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ Ｐ(Ａ Ｂ) Ｐ(Ａ ) Ｐ(Ｂ｜ Ａ ) 所以Ｐ(Ａ ｜ Ｂ) ＝ ３ ＝ ３ ３ ＝ ０􀆰３ ＝ ３０. 分 ３ Ｐ(Ｂ) Ｐ(Ｂ) 􀆺􀆺􀆺􀆺􀆺 １１ ０􀆰７１ ７１ 即采摘出的某颗水仙花球茎经雕刻后能使用 它是由丙工作队所采摘的概率为 ꎬ ３０. 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ７１ 数学第一次教学质量检测参考答案 第 ４页 (共６页). 分 ２１ (１２ ) 解 当直线ｌ斜率不存在时 其方程为ｘ ＝ 符合题意 分 : (１) ꎬ ０ꎬ ꎻ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ 当直线ｌ斜率存在时 设直线ｌ的方程为ｙ ＝ ｋｘ ＋ 分 ꎬ １ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ２ {ｙ ＝ ｋｘ ＋ 由 １ 得ｋ２ｘ２ ＋ ( ｋ － ) ｘ ＋ ＝ 分 ｙ２ ＝ ｘ ꎬ ２ ４ １ ０􀆰 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ３ ４ 当ｋ ＝ 时 直线ｙ ＝ 符合题意 分 ０ ꎬ １ ꎻ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ４ 当ｋ 时 令Δ ＝ ( ｋ － ) ２ － ｋ２ ＝ － ｋ ＝ 解得ｋ ＝ ≠０ ꎬ ２ ４ ４ １６ １６ ０ꎬ １ꎬ 直线ｌ的方程为ｙ ＝ ｘ ＋ 即ｘ － ｙ ＋ ＝ 分 ∴ １ꎬ １ ０􀆰 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ 综上 直线ｌ的方程为ｘ ＝ 或ｙ ＝ 或ｘ － ｙ ＋ ＝ . 分 ꎬ ０ꎬ １ꎬ １ ０ 􀆺􀆺􀆺􀆺􀆺􀆺 ６ 解法一 设Ｑ ｘ ｙ Ａ ｘ ｙ Ｂ ｘ ｙ 不妨令ｘ < ｘ (２) : ( 􀆯 )ꎬ ( １􀆯 １)ꎬ ( ２􀆯 ２)ꎬ １ ２ꎬ {ｋ 直线ｌ与抛物线Ｃ有两个交点 ≠０ ∵ ꎬ ∴ Δ ＝－ ｋ ＋ > ꎬ １６ １６ ０ ｋ < 且ｋ 分 ∴ １ꎬ ≠０ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ － ｋ ｘ ＋ ｘ ＝ ４ ２ ｘ ｘ ＝ １ 分 １ ２ ｋ２ ꎬ １ ２ ｋ２ 􀆰 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ８ ＡＰ ＡＱ ｘ ｘ － ｘ ｘ ｘ 由 ＝ 得 １ ＝ １ ｘ ＝ ２ １ ２ ＝ １ ＰＢ ＱＢ ꎬ ｘ ｘ － ｘꎬ ∴ ｘ ＋ ｘ － ｋꎬ ２ ２ １ ２ ２ ｋ ｙ ＝ ＋ ＝ ２ 分 ∴ － ｋ １ － ｋꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ ２ ２ ｙ ＝ ｘ 分 ∴ ２ 􀆰 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ ｋ < 且ｋ < ｘ < 且ｘ １ ∵ １ꎬ ≠０ꎬ ∴ ０ １ꎬ ≠ ꎬ ２ 点Ｑ的轨迹方程为ｙ ＝ ｘ < ｘ < 且ｘ １ 分 ∴ ２ (０ １ꎬ ≠ )􀆰 􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ２ 解法二 设Ｑ ｘ ｙ Ａ ｘ ｙ Ｂ ｘ ｙ 不妨令ｘ < ｘ : ( ꎬ )ꎬ ( １ꎬ １)ꎬ ( ２ꎬ ２)ꎬ １ ２ꎬ {ｋ 直线ｌ与抛物线Ｃ有两个交点 ≠０ ｋ < 且ｋ ∵ ꎬ ∴ Δ ＝－ ｋ ＋ > ꎬ ∴ １ꎬ ≠０ꎬ １６ １６ ０ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ － ｋ ｘ ＋ ｘ ＝ ４ ２ ｘ ｘ ＝ １ 分 １ ２ ｋ２ ꎬ １ ２ ｋ２ 􀆰 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ８ ｜ ＡＰ｜ ｜ ＡＱ｜ 点Ｑ在线段ＡＢ上 设 ＝ ＝ λ 则Ｐ→Ａ ＝ λ Ｐ→Ｂ Ａ→Ｑ ＝ λ Ｑ→Ｂ ∵ ꎬ ｜ ＰＢ｜ ｜ ＱＢ｜ ꎬ ꎬ ꎬ {ｘ ＝ λｘ ｘ ｘ ｋ １ ２ ｘ ＝ ２ １ ２ ＝ １ ｙ ＝ ＋ ＝ ２ ∴ ｘ － ｘ ＝ λ ｘ － ｘ ꎬ ∴ ｘ ＋ ｘ － ｋꎬ ∴ － ｋ １ － ｋꎬ １ ( ２ ) １ ２ ２ ２ ２ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ ｙ ＝ ｘ 分 ∴ ２ 􀆰 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ ｋ < 且ｋ < ｘ < 且ｘ １ ∵ １ꎬ ≠０ꎬ ∴ ０ １ꎬ ≠ ꎬ ２ 点Ｑ的轨迹方程为ｙ ＝ ｘ < ｘ < 且ｘ １ 分 ∴ ２ (０ １ꎬ ≠ )􀆰 􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ２ 数学第一次教学质量检测参考答案 第 ５页 (共６页). 分 ２２ (１２ ) 解 ｆ(ｘ) 的定义域为(－ ＋ ¥) ｆ ′(ｘ) ＝ (ｘ ＋ ) － λ ＋ 分 : (１) １􀆯 ꎬ ｌｎ １ １􀆯 􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ 因为ｆ ′(ｘ) 在[ ＋ ) 上单调递增 ｆ ′( ) ＝－ λ ＋ 分 ０􀆯 ∞ ꎬ ０ １ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ２ 当λ 时 对于任意的ｘ [ ＋ ) 有ｆ ′(ｘ) ｆ ′( ) ① ≤１ ꎬ ∈ ０􀆯 ∞ ꎬ ≥ ０ ≥０ꎬ 所以ｆ(ｘ) 在[ ＋ ) 上单调递增 ０􀆯 ∞ ꎬ 则对于任意的ｘ [ ＋ ) ｆ(ｘ) ｆ( ) ＝ ∈ ０􀆯 ∞ ꎬ ≥ ０ ０ꎬ 所以λ 符合题意 分 ≤１ ꎻ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ４ 当λ > 时 令ｆ ′(ｘ) > 得ｘ > ｅλ－ １ － ② １ ꎬ ０ꎬ １ꎬ 令ｆ ′(ｘ) < 得 ｘ < ｅλ－ １ － ０ꎬ ０≤ １ꎬ 所以ｆ(ｘ) 在[ ｅλ－ １ － ) 上单调递减 ｆ(ｘ) 在(ｅλ－ １ － ＋ ) 上单调递增 ０􀆯 １ ꎬ １􀆯 ∞ ꎬ 则ｆ(ｅλ－ １ － ) < ｆ( ) ＝ 这与当ｘ 时 ｆ(ｘ) 矛盾 所以λ > 舍去 １ ０ ０ꎬ ≥０ ꎬ ≥０ ꎬ １ ꎻ 综上 λ 所以λ 的最大值为 . 分 ꎬ ≤１ꎬ １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ６ 由 可知 当ｘ > 时 (２) (１) ꎬ ０ ꎬ 有(ｘ ＋ ) (ｘ ＋ ) － ｘ > 即 １ < (ｘ ＋ ) １ ｌｎ １ ０ꎬ ｌｎ １ ꎬ ＋ １ １ ｘ æ ö ｎ ＋ 令ｘ ＝ １ ｎ Ｎ∗ 则 １ < ç １ ＋ ÷ ＝ １ ＝ (ｎ ＋ ) － ｎ ｎꎬ ∈ ꎬ ＋ ｎ ｌｎè ｎ １ø ｌｎ ｎ ｌｎ １ ｌｎ ꎬ １ 所以 １ < (ｎ ＋ ) － ｎ １ < (ｎ ＋ ) － (ｎ ＋ ) ｎ ＋ ｌｎ １ ｌｎ ꎬ ｎ ＋ ｌｎ ２ ｌｎ １ ꎬ 􀆺ꎬ １ ２ １ < ( ｎ) － ( ｎ － ) 分 ｎ ｌｎ ２ ｌｎ ２ １ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ ２ 将以上不等式左右两边分别相加 得 ꎬ １ ＋ １ ＋ ＋ １ < ( ｎ) － ｎ ＝ 分 ｎ ＋ ｎ ＋ 􀆺 ｎ ｌｎ ２ ｌｎ ｌｎ２ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ １ ２ ２ 所以 － １ ＋ １ － １ ＋ ＋ １ － １ １ 􀆺 ｎ － ｎ ２ ３ ４ ２ １ ２ æ ö æ ö ＝ ç ＋ １ ＋ １ ＋ １ ＋ ＋ １ ＋ １ ÷ － ç １ ＋ １ ＋ ＋ １ ÷ è１ 􀆺 ｎ － ｎø ２è 􀆺 ｎø ２ ３ ４ ２ １ ２ ２ ４ ２ æ ö æ ö ＝ ç ＋ １ ＋ １ ＋ １ ＋ ＋ １ ＋ １ ÷ － ç １ ＋ １ ＋ ＋ １ ÷ è１ 􀆺 ｎ － ｎø è 􀆺 ｎ ø ２ ３ ４ ２ １ ２ １ ２ ＝ １ ＋ １ ＋ ＋ １ < . 分 ｎ ＋ ｎ ＋ 􀆺 ｎ ｌｎ２ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ １ ２ ２ 数学第一次教学质量检测参考答案 第 ６页 (共６页)