文档内容
2024 年普通高等学校招生全国统一考试(新课标 II 卷)
数学
本试卷共10页,19小题,满分150分.
注意事项:
1.答题前,先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,并将准考
证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试
卷、草稿纸和答题卡上的非答题区域均无效.
3.填空题和解答题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草
稿纸和答题卡上的非答题区域均无效.
4.考试结束后,请将本试卷和答题卡一并上交.
一、单项选择题:本大题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,
只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1. 已知 ,则 ( )
A. 0 B. 1 C. D. 2
.
2 已知命题p: , ;命题q: , ,则( )
A. p和q都是真命题 B. 和q都是真命题
C. p和 都是真命题 D. 和 都是真命题
3. 已知向量 满足 ,且 ,则 ( )
A. B. C. D. 1
4. 某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(单位:kg)并
整理如下表
[1150
[900, [950, [1000, [1050, [1100,
亩产量 ,
950) 1000) 1050) 1100) 1150)
1200)
频数 6 12 18 30 24 10
根据表中数据,下列结论中正确的是( )A. 100块稻田亩产量的中位数小于1050kg
B. 100块稻田中亩产量低于1100kg的稻田所占比例超过80%
C. 100块稻田亩产量的极差介于200kg至300kg之间
D. 100块稻田亩产量的平均值介于900kg至1000kg之间
5. 已知曲线C: ( ),从C上任意一点P向x轴作垂线段 , 为垂足,则线段
的中点M的轨迹方程为( )
A. ( ) B. ( )
C. ( ) D. ( )
.
6 设函数 , ,当 时,曲线 与 恰有
一个交点,则 ( )
A. B. C. 1 D. 2
7. 已知正三棱台 的体积为 , , ,则 与平面ABC所成角的正切值为
( )
A. B. 1 C. 2 D. 3
8. 设函数 ,若 ,则 的最小值为( )
.
A B. C. D. 1
二、多项选择题:本大题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的四个选项中,
有多项符合题目要求. 全部选对得 6 分,选对但不全的得部分分,有选错的得0分.
9. 对于函数 和 ,下列说法中正确的有( )
A. 与 有相同的零点 B. 与 有相同的最大值C. 与 有相同的最小正周期 D. 与 的图象有相同的对称轴
10. 抛物线C: 的准线为l,P为C上的动点,过P作 的一条切线,Q为切点
过P作l的垂线,垂足为B,则( )
A. l与 相切
B. 当P,A,B三点共线时,
C. 当 时,
D. 满足 的点 有且仅有2个
11. 设函数 ,则( )
.
A 当 时, 有三个零点
B. 当 时, 是 的极大值点
C. 存在a,b,使得 为曲线 的对称轴
D. 存在a,使得点 为曲线 的对称中心
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12. 记 为等差数列 的前n项和,若 , ,则 ________.
13. 已知 为第一象限角, 为第三象限角, , ,则
_______.
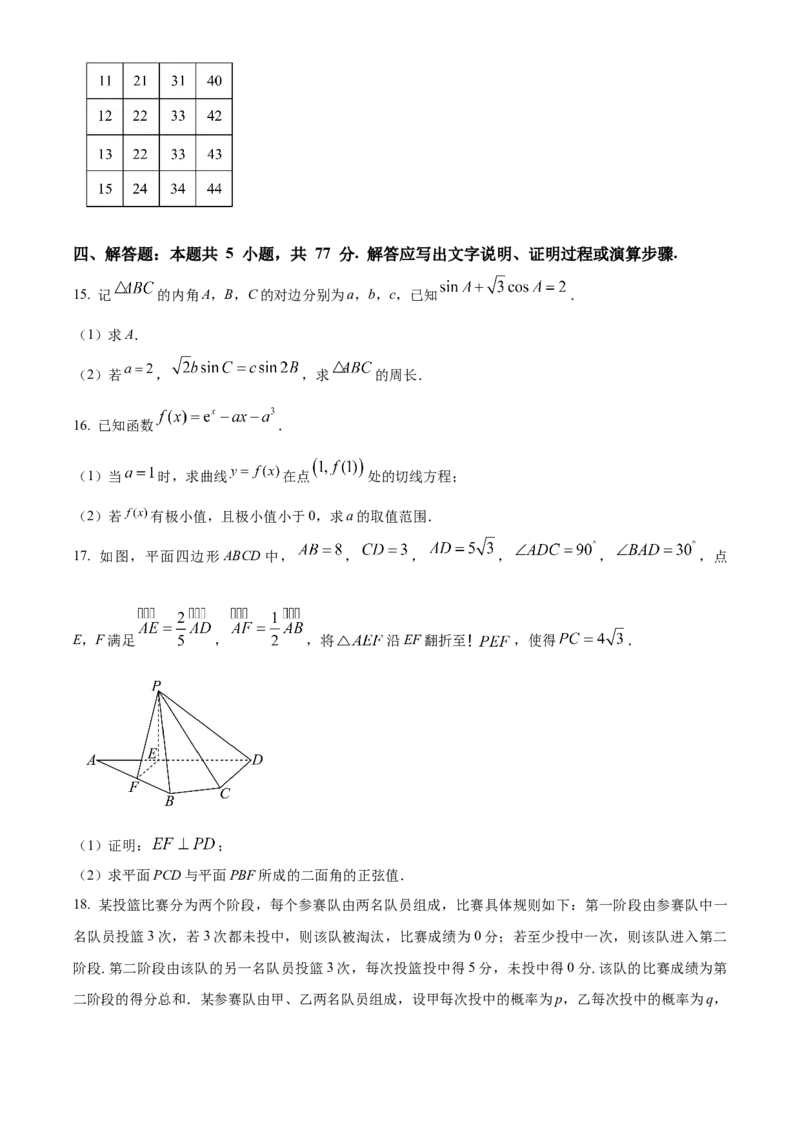
14. 在如图的4×4的方格表中选4个方格,要求每行和每列均恰有一个方格被选中,则共有________种选法
在所有符合上述要求的选法中,选中方格中的4个数之和的最大值是________.四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15. 记 的内角A,B,C的对边分别为a,b,c,已知 .
(1)求A.
(2)若 , ,求 的周长.
16. 已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)若 有极小值,且极小值小于0,求a的取值范围.
17. 如图,平面四边形ABCD中, , , , , ,点
E,F满足 , ,将 沿EF翻折至 ,使得 .
(1)证明: ;
(2)求平面PCD与平面PBF所成的二面角的正弦值.
18. 某投篮比赛分为两个阶段,每个参赛队由两名队员组成,比赛具体规则如下:第一阶段由参赛队中一
名队员投篮3次,若3次都未投中,则该队被淘汰,比赛成绩为0分;若至少投中一次,则该队进入第二
阶段.第二阶段由该队的另一名队员投篮3次,每次投篮投中得5分,未投中得0分.该队的比赛成绩为第
二阶段的得分总和.某参赛队由甲、乙两名队员组成,设甲每次投中的概率为p,乙每次投中的概率为q,各次投中与否相互独立.
(1)若 , ,甲参加第一阶段比赛,求甲、乙所在队的比赛成绩不少于5分的概率.
(2)假设 ,
(i)为使得甲、乙所在队的比赛成绩为15分的概率最大,应该由谁参加第一阶段比赛?
的
(ii)为使得甲、乙所在队 比赛成绩的数学期望最大,应该由谁参加第一阶段比赛?
19. 已知双曲线 ,点 在 上, 为常数, .按照如下方式依次构
造点 :过 作斜率为 的直线与 的左支交于点 ,令 为 关于 轴的对称点,
记 的坐标为 .
(1)若 ,求 ;
(2)证明:数列 是公比为 的等比数列;
(3)设 为 的面积,证明:对任意正整数 , .