文档内容
2023 年 8 月学科能力综合测试 (TACA)
丘成桐数学零试试题及解析
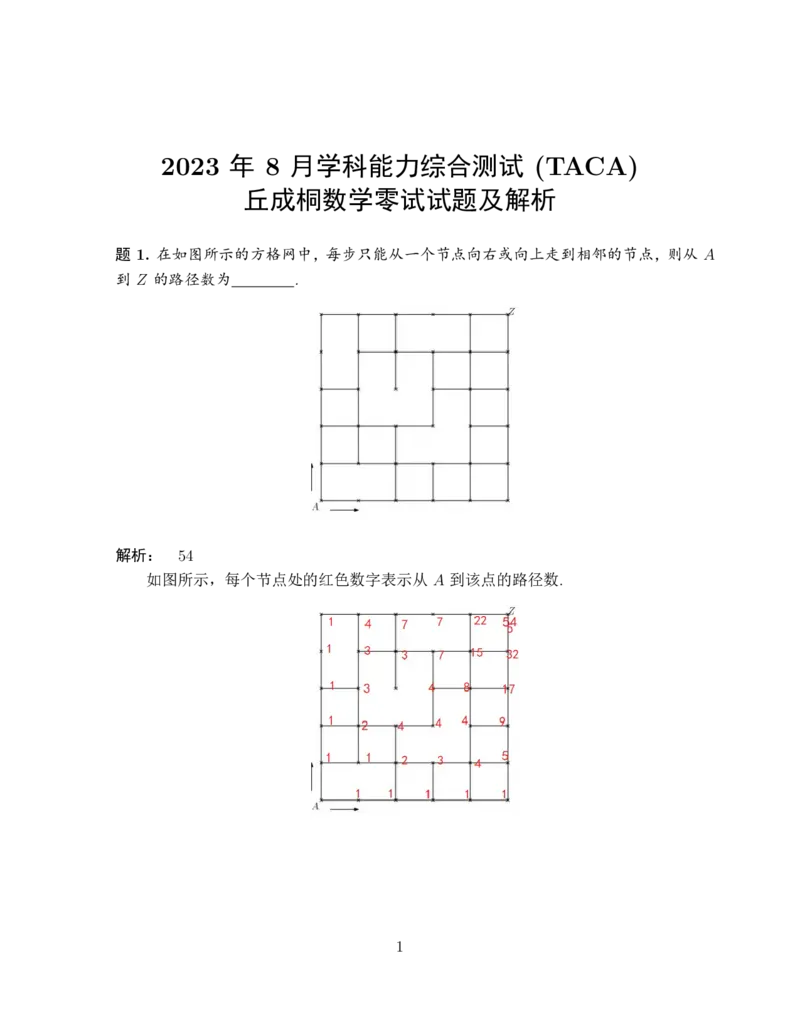
题 1. 在如图所示的方格网中,每步只能从一个节点向右或向上走到相邻的节点,则从 A
到 Z 的路径数为 .
解析: 54
如图所示,每个节点处的红色数字表示从 A 到该点的路径数.
1
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}( )
∑∞ −5π 3π
题 2. 对一个复方阵,定义 cosA = I + (−1)n A2n. 记矩阵 cos 的第二行
(2n)! −10π 6π
n=1
第一列元素为 x,则 [|x|] = .
解析: 20 ( )
−5π 3π
令 M = ,易知 M 的特征多项式为 f(λ) = λ(λ − π),故其特征值为
−10π 6π
0,π. 解出对应特征向量后,易知
( )( )( )
−1
3 1 0 3 1
M =
5 2 π 5 2
于是
( )( )( ) ( )
−1
3 1 1 3 1 11 −6
cosM = =
5 2 −1 5 2 20 −11
故所求答案为 20.
∫
题 3. I = lim 2023 cos4(nx+n!)dx,则 [100I] = .
n→∞ 1
解析: 758
∫
I = lim 2023 cos4(nx+n!)dx,则 [100I] =
n→∞ 1 ∫
我们令 I = 2023 cos4(nx+n!)dx。则
n 1
∫ ( ) ∫ ( )
2023 1+cos(2nx+2·n!) 2 2023 1 1 1
I = = + cos(2nx+2·n!)+ cos2(2nx+2·n!) dx
n
2 4 2 4
1 ∫ 1 ∫
2022 1 2023 1 2023 1+cos(4nx+4·n!)
= + cos(2nx+2·n!)dx+ dx
4 2 4 2
1∫ 1 ∫
2022 1 2023 2022 1 2023
= + d(sin(2nx+2·n!))+ + d(sin(4nx+4·n!))
4 2n 8 8·4n
1 1
∫ ∫
显然 2023 d(sin(2nx+2·n!))和 2023 d(sin(4nx+4·n!))有界,故I = lim I = 3×2022,
1 1 n→∞ n 8
故 [I] = 758.
∫ ∫
题 4. 设 g(x) = π (sint)5 dt,记 S = π g(x)dx,则 [100S] = .
x t 0
2
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}解析: 106
∫ ∫ ∫ ∫ ∫
π π (sint)5 π (sint)5 t π
S = dx dt = dt dx = (sint)5dt
t t
0∫ x 0 0 0
注意到令 I = π sinntdt,则由熟知的结论,有 I = n−1I (n > 2),所以
n 0 n n n−2
4×2 16
S = I = I = ,
5 5×3 1 15
于是 [100S] = 106.
题 5. n×n 矩阵 A 的主对角元素为 n,其余元素为 1. 已知多项式 f(x) 满足 f(A ) = O
n n
对任意 1 6 n 6 100 均成立,则 degf 的最小值为 .
解析: 149
n × n 矩阵 A 的主对角元素为 n,其余元素为 1. 已知复系数多项式 f(x) 满足
f(A ) = O 对任意 1 6 n 6 100 均成立,则 degf 的最小值为 .
n
记 f (x) 为 A 的首相系数为 1 的最小多项式,则显然对任意 1 6 n 6 100,均有
n n
f (x) | f(x). 接下来我们求 f (x).
n n
n = 1 时,显然 f (x) = x−1.
1
n > 2时,因为A 为实对称矩阵,所以A 可对角化. 注意到rank(A −(n−1)I ) = 1,
n n n n
所以 n−1 为 A 的特征值,其特征子空间维数为 n−1. 又因为 A 全体特征值 (计重
n n
数) 之和为 trace(A ) = n2,所以 A 剩余特征值为 n2 − (n − 1)2 = 2n − 1. 于是
n n
f (x) = (x−(2n−1))(x−(n−1)).
n
f (x),f (x),··· ,f (x) 包含的互不相同的一次式有
1 2 n
x−1,x−2,··· ,x−98,x−99,x−101,x−103,··· ,x−199
f(x) 需且仅需被这些一次式整除即可,故 degf 的最小值为 149.
3
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}题 6. 矩阵
10 −9 −9
−9 10 −9
−9 10 −9
−9 10 −9
−9 10 −9
−9 10 −9
−9 10 −9
−9 −9 10
的特征值为 λ 6 λ 6 ··· 6 λ ,则 [λ ] = .
1 2 8 6
解析: 22
显然该矩阵为循环矩阵,令
1
1
1
1
J =
1
1
1
1
由熟知的结论,J 的全部特征值即为全体 8 次单位根 ϵ (i = 0,1,··· ,7), 令 f(x) =
i
−9x7 − 9x + 10,则原矩阵为 f(J), 故该矩阵全部特征根为 f(ϵ ),注意到 ϵ = ϵ7(i =
i i i
0,1,··· ,7),所以 f(ϵ ) 均为实数,且可能取值为
i
√ √
10−18,10−9 2,10,10+9 2,10+18
√
故 λ = 10+9 2,[λ ] = 22.
6 6
题 7. 在透明的球袋中有 1 个黑球和 2 个白球. 接下来从袋中摸球,每次摸出一个球,然
后放回袋中,并继续往袋中再放入 2 个与摸出球同色的球. 记 S 为前 n 次中摸出黑球
n
的次数. 已知第 2 次摸出的球是黑球,记 S 的期望为 E,则 [E] = .
100
4
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}解析: 60
我们计算 E(S | S ). 这时一共有 1+2S 个黑球和 2+2(n−1−S ) 个白球.
n n−1 n−1 n−1
则第 n 次有 1+2Sn−1 的概率摸到黑球,故
3+2(n−1)
1+2S
E(S | S ) = S + n−1
n n−1 n−1
2n+1
因为 E(S ) = E(E(S | S )),所以
n n n−1
1+2S
n−1
E(S ) = E(S )+E( )
n n−1
2n+1
1 2n+3
⇒ E(S ) = + E(S )
n n−1
2n+1 2n+1
1 1 1
⇒ E(S ) = + E(S )
n n−1
2n+3 (2n+1)(2n+3) 2n+1
故
E(S ) E(S ) 1 1
n = 2 + −
2n+3 7 14 4n+6
因为已知第二次摸出的是黑球,所以
1/3×3/5 2/3×1/5 8
E(S ) = ×2+ ×1 =
2 1/3×3/5+2/3×1/5 1/3×3/5+2/3×1/5 5
于是
8 1 203 1
[E] = [E(S )] = [203× × + − ] = 60
100
5 7 14 2
题 8. 对矩阵 M(t),定义其微分 dM(t) = B(t),其中 dM (t) = B (t). 矩阵微分方程
dt dt ij ij
d
M(t) = AM(t),
dt
其中
2 1 3 3 2 1
A = 1 3 2, M(0) = 2 1 3,
3 2 1 1 3 2
令 a = ln|detM(2)|, 则 [|a|] = .
5
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}解析: 14
由常微分方程熟知结论,M(t) = M(0)eAt. 计算可得 A 的特征多项式 f(λ) = |λI −
√ √ √
A| = (λ−6)(λ− 3)(λ+ 3),于是 A 的特征值为 6,± 3,由于 A 是实对称矩阵,所
以存在正交矩阵 T,使得
6
√
A = T 3 T ′ , TDT ′
√
− 3
于是
|detM(2)| = |detM(0)||e2D| = |−18e12| = 18e12
故 [|a|] = [ln18+12] = 14.
题 9. 5 级方阵 A 满足:第一行元素均为 1,第二行元素从左至右依次为 1,−1,1,−1,1,
且 trace(AA′) = 28. 记 detA 的最大值为 M,则 [M] = .
解析: 72
∑
5
我们记 A = (α ,α ,··· ,α )′,于是由 trace(AA′) = 28,有 |α |2 = 28,注意到
1 2 5 i
i=1
∑
5
|α |2 = |α |2 = 5,所以 |α |2 = 18.
1 2 i
i=3
由熟知的结论,存在正交矩阵 (变换)T,使得 AT = (β ,β ,··· ,β )′ 为上三角矩阵. 设
1 2 5
该上三角矩阵的主对角元依次为 a ,a ,··· ,a . 则有正交变换的性质可知,|α | = |β |(i =
1 2 5 i i
1,2,··· ,5),且 1 =< α ,α >=< β ,β > 于是
1 2 1 2
∑5 ∑5
|a |2 6 |α |2 = 18
i i
i=3 i=3
24
1 =< β ,β >26 (5−a2)×5 ⇒ a2 6
1 2 1 1 5
a2 6 |β |2 = 5
2 2
于是 …
√ √
24
|detA| = |a a a a a | 6 ( 6)3 · · 5 = 72
1 2 3 4 5
5
6
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}取得 72 时, » »
24 1
5 √5
5
√
AT = 6
√
6
√
6
我们只需构造使得前两行可以对应的正交矩阵 T 即可得到满足条件的 A.
∫
题 10. 对 n = 5,令 L = 1 dn (x2 −1)n,S = 1 |L |2dx,则 [|S|] = .
n n!dxn −1 n
解析: 186
令 f (x) = (x2 −1)n. 易知 ±1 均为 f (x) 的 n 重根,所以
n n
f(k)(1) = f(k)(−1) = 0, 0 6 k 6 n−1.
n n
于是 ∫ ∫
1 1 1 1
S = (f(n)(x))2dx = d(f(n−1)(x))f(n)(x)
(n!)2 n (n!)2 n n
−∫1 −1
1 1
= − f(n+1)(x)f(n−1)(x)dx
(n!)2 n n
∫−1
1 1
= − f(n+1)(x)d(f(n−2)(x))
(n!)2 n n
∫ −1
1 1
=
f(n+2)(x)f(n−2)(x)dx
(n!)2 n n
−1
······
∫
1 1
= f(2n)(x)f(0)(x)dx
(n!)2 n n
∫−1
1 1
= (2n)!(1−x2)ndx
(n!)2
−1 ∫
1 1
= (1−x2)ndx
(n!)2(2n)!
∫ −1
(2n)! π (2n)! 2(2n)!!
= sin2n+1dt =
(n!)2 (n!)2 (2n+1)!!
0
所以 [S] = [ 10! × 2×10×8×···×2] = [2048] = 186.
(5!)2 11×9×···×1 11
7
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}题 11. 正方体旋转群元素最多的两个共轭类的元素个数之和为 .
解析: 14
由熟知的结论正方体旋转群同构于 S . 所以两元素共轭等价于其分解成不叫的轮换
4
和后,各个轮换和的长度对应相等. 故元素最多的共轭类形如 (abc)(d),有 4×2! = 8 个
元素,元素次多的共轭类形如 (abcd),共有 3! = 6 个元素,所求答案为 8+6 = 14
∑∞ ∑∞
题 12. A(x) = m!·xm·n! ,则 [100A(2)] = .
(m+n+1)! 3
m=1n=0
解析: 109
∑∞
令 a = n! ,则
m (n+m+1)!
n=0
∑∞
n!
a =
m
(n+m+1)!
n=0 ( )
∑∞
1 n! (n+1)!
= −
m (n+m)! (n+m+1)!
n=0
1 1
=
mm!
于是 |x| < 1 时,
∑∞
1
A(x) = xm = −ln(1−x)
m
m=1
所以 [100A(2)] = [100ln3] = 109
3
题 13. 将方程 (1+2+···+k)−3(1+2+···+t) = 1 的全体正整数解 (k,t) 按照从小
到大的方式排列,得到序列 {(k ,t )},则 k = .
n n 6
解析: 3196
对原方程进行变形,有
k(k +1)−3t(t+1) = 2 ⇒ (2k +1)2 −3(2t+1)2 = 6
令 2k +1 = u,2t+1 = v. 考虑虑方程
u2 −3v2 = 6
8
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}的所有正整数解由小到大构成的序列 {(u ,v )} ,则由佩尔方程基本理论有
n n n>1
√ √ √
u + 3v = (3+ 3)(2+
3)n−1
n n
于是有
√ √ √ √
u + 3v = (u + 3v )(2+ 3) = 2u −3v = (2u +3v )+ 3(u +2v )
n n n−1 n−1 n−1 n−1 n−1 n−1 n−1 n−1
u = 2u +3v
即 n n−1 n−1 ,则我们依次写出 {(u ,v )} 的前 7 项:
n n
v = u +2v
n n−1 n−1
(3,1),(9,5),(33,19),(123,71),(459,265),(1713,989),(6393,3691)
注意到 (3,1) 对应的 (k,t) 不满足正整数的条件,所以 k = 6393−1 = 3196.
6 2
∫ [ ]
题 14. I = π/4 tan101xdx,则 1 .
0 3I
解析: 67
∫
记 I = π/4 tannxdx,则
n 0
∫ ∫
π/4 sinnx π/4 sinn−1xd(−cosx)
I = dx = dx
n cosnx cosnx
0 ∫ 0
π/4
= −1+ ((n−1)tann−2x+ntannx)dx
0
= −1+(n−1)I +nI
n−2 n
于是
1
I +I = , n > 2
n n−2 n−1
故
1 1 1
I = −I = − +I
99 97
100 100 98
······
1 1 1 1
= − + −···− +I
1
10(0 98 96 ) 2
∑50
1 1
= ln2+ (−1)k
2 k
k=1
注意到
∑50 ∑∞ ∑∞ ∑∞
1 1 1 1
(−1)k = (−1)k − (−1)k = −ln2− (−1)k
k k k k
k=1 k=1 k=51 k=51
9
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}所以
∑∞
1
I = − (−1)k
k
k=51 ( )
∑∞
1 1 1
= − −
51 2k 2k +1
k=26
∑∞
1 1 1
= −
51 4 k(k +1/2)
k=26( )
∑∞
1 1 1 1 1 1 52
> − − = − =
51 4 k −1/4 k +3/4 51 103 5253
k=26
且
∑∞
1 1 1
I = −
51 4 k(k +1/2)
k=26( )
∑∞
1 1 1 1 1 1 52.5
< − − = − =
51 4 k −1/8 k +7/8 51 103.5 5278.5
k=26
故
5278.5×2 1 5253×2
67 < < < < 68
3×52.5 3I 3×52
于是 [ 1 ] = 67.
3I
题 15. M = {A|A是n级实对称矩阵, 且元素取自0,±1,±2},记a 为所有trace(A6)(A ∈
n n
M ) 的平均值,a = lim sup an,则 [a] = .
n k→∞ n>k n4
解析: 40
令 T = {0,±1,±2},则
∑ ∑
S = 5n(n+1)/2a = a a ···a
n n t1t2 t2t3 t6t1
∑ a ∑ij ∈T,i6j06t1,t2,···,t6 6n
= a a ···a
t1t2 t2t3 t6t1
06t1,t2,···,t6 66aij ∈T,i6j
对 a a ···a 项而言,我们关心 a (i 6 j) 遍历所有 T 中元素后,这样的项得
t1t2 t2t3 t6t1 ij
到的总和. 我们称 a 和 a 为“同组”的元素. 注意到 x ∈ T ⇔ −x ∈ T,且 a (i 6 j)
ij ji ij
彼此的取值独立,所以若某组元素在 a a ···a 中出现奇数次,则 a a ···a
t1t2 t2t3 t6t1 t1t2 t2t3 t6t1
在和式中累加后为 0. 所以我们只需考虑以下三种情形:
(1)情形1:a a ···a 由仅有同组元素构成,即形如a a ···a 或a a a ···a
t1t2 t2t3 t6t1 t1t1 t1t1 t1t1 t1t2 t2t1 t1t2 t2t1
10
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}易知这样的项在 S 中的总和形如 Pn5n(n+1)/2+Qn(n−1)5n(n+1)/2,其中 P,Q 为常
n
数.
(2) 情形 2:a a ···a 由恰由两组元素构成,一组出现 2 次,一组出现 4 次.
t1t2 t2t3 t6t1
易知这样的项在 S 中的总和形如 Un(n−1)5n(n+1)/2,其中 U 为常数.
n
(3) 情形 3:a a ···a 由恰由三组元素构成,每组出现 2 次.
t1t2 t2t3 t6t1
首先易知此时不存在 t = t 的情形,于是 t ,t ,··· ,t 中同样的下标至多出现 3
i i+1 1 2 6
次. 我们下面按照 t ,t ,··· ,t 中不同取值的个数分类,易知只有两种情况:
1 2 6
(i)t ,t ,··· ,t 有三种不同取值
1 2 6
此时这样的项在 S 中的总和形如 Rn(n−1)(n−2)5n(n+1)/2,其中 R 为常数.
n
(ii)t ,t ,··· ,t 有四种不同取值,记为 x,y,z,w. 此时,t ,t ,··· ,t 可能的的排列只
1 2 6 1 2 6
有
xyxzxw,xyzywy,xyzyxw,xyxzwz,xyzwzy
这五种情形,其在 S 中总和形如 Vn(n−1)(n−2)(n−3)5n(n+1)/2,其中 V 为常数.
n
于是
S = 5n(n+1)/2(Pn+Qn(n−1)+Rn(n−1)(n−2)
+Vn(n−1)(n−2)(n−3))
所以
a S
n n
lim sup = lim sup = V
k→∞ n>k n4 k→∞ n>k n45n(n+1)/2
所以我们只需求出 V 即可.
所有满足 t ,t ,··· ,t 取值形如 x,x,x,y,z,w 的 a a ···a 之和为
1 2 6 t1t2 t2t3 t6t1
∑
5n(n−1)(n−2)(n−3)5n(n+1)/2−3 p2q2r2
p,q,r∈T
= 2n(n−1)(n−2)(n−3)5n(n+1)/2−3(02 +2×12 +2×22)3
5×103
= n(n−1)(n−2)(n−3)5n(n+1)/2
53
5×103
故 V = = 40.
53
11
{#{QQABKYiUggCgAAAAABgCQQ0gCgEQkBGACAgGRAAAMAIASAFABAA=}#}