2023年9月THUSSAT中学生标准学术能力高三上学期诊断性测试数学试卷（含答案）(1)_2023年9月_029月合集_全科THUSSAT中学生标准学术能力诊断性测试高三上学期9月测试

中学生标准学术能力诊断性测试 2023 年 9 月测试 数学试卷 本试卷共 150分，考试时间 120分钟。 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是 符合题目要求的．  x−1 1    1．设集合A=x  ,xR,B= xN1 x5 ，则  x+2 2  第1页 共4页 第2页 共4页 A B = A． 2 B．  2 , 3  C．  3 , 4  D． 2,3,4 2．欧拉公式ei=cos+isin把自然对数的底数 e 、虚数单位 i 、三角函数联系在一起，充分体现 了数学的和谐美．已知实数指数幂的运算性质同样也适用于复数指数幂，则 i i =   A． B． − C． e2 e 2 e  D． e −  3．已知等比数列  a n  的前n项和为 S n ，若S =S +16S ，则公比q= 12 4 8 A．3 B．  2 C． 2 D．3 4．已知向量ABAC =6，线段 B C 的中点为 M ，且 A M = 6 ，则 BC = A．2 30 B． 3 3 0 C． 2 2 6 D． 3 2 6   5．已知函数 f (x)=sin  x+  (0) 的周期为  3 T 的最大值为 A．1 B．2 C．3 D．4 11 10 1 8．比较a= − ,b=ln1.2,c= 的大小 10 11 5e0.1 A． ，且满足T 2，若函数 f (x) 在区间    , 不单调，则的取值范围是 6 4   1  2  4  A． ,1  B． ,1  C． ,1  D． ,1  4  2  3  5    6．三棱锥A−BCD中，AB=3,BC =BD=4 2,ABC =ABD= ,DBC = ，则直线AD 4 3 与平面ABC所成角的正弦值是 4 17 4 29 3 17 3 29 A． B． C． D． 17 29 17 29 BD 1 7．已知三角形ABC中，BC =3，角A的平分线交BC于点D，若 = ，则三角形ABC面积 DC 2 a  c  b B． b  c  a C． b  a  c D． a  b  c 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合 题目要求．全部选对得5分，部分选对但不全得3分，有错选的得0分. 9．已知实数abc满足 a  b  c ，且 a b c = 1 ，则下列说法正确的是 1 A．(a+c)2  b C． a 2  b 2 B． a 1 − c  b 1 − c D． ( a2b−1 )( ab2 −1 ) 0 10．已知10个样本数据，若去掉其中最大和最小的数据，设剩下的8个样本数据的方差为 s 21 ，平均 数 x 1 ；最大和最小两个数据的方差为 s 22 ，平均数 x 2 ；原样本数据的方差为 S 2 ，平均数x，若 x 1 = x 2 ，则 A．剩下的8个样本数据与原样本数据的中位数不变 B． x = x 1 C．剩下8个数据的下四分位数大于与原样本数据的下四分位数 4 1 D．S2 = s2 + s2 5 1 5 2 11．已知函数 f (x)=cos2x+2sinx ，则   A．函数 f (x) 在区间 , 上单调递增 6 2  B．直线x = 是函数 f (x) 图象的一条对称轴 2  3 C．函数 f (x) 的值域为 1,    2 D．方程 f (x)=a ( x(0,2)) 最多有8个根，且这些根之和为 x2 12．已知椭圆C: + y2 =1的中心为O， A,B是C 上的两个不同的点且满足OA⊥OB，则 2 A．点O在直线AB上投影的轨迹为圆 {#{QQABCQqQogAgABIAAQhCQQVCCkCQkBEACAoGAFAAIAABwQFABAA=}#}B．AOB的平分线交 第3页 共4页 第4页 共4页 A B 于D点， O D 6 的最小值为 3 2 C．AOB面积的最小值为 3 2 3 D．AOB中，AB边上中线长的最小值为 3 三、填空题：本题共4小题，每小题5分，共20分． 13．已知tan=2，则 s i n 4  = ． 14．若 ( x2 −x−3 )5 =a +a x+a x2 + +a x10，则a +a +a +a +a = ． 0 1 2 10 1 2 3 4 5 15．已知四棱锥的各个顶点都在同一个球面上．若该球的体积为 3 6  ，则该四棱锥体积的最大值 是 ． 1 16．已知函数 f (x)=ex +msinx− x2 −(m+1)x+1，在 2 x = 0 处取到极小值，则实数 m = ． 四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10 分）已知  a n  是各项均为正数的等比数列，设c =log a ，若数列 n 3 n  c n  的前 n 项和 n2 +n S = ． n 2 （1）求数列 a  的通项公式； n （2）记d =a  ( 2n2 +6n+5 ) ，求数列 n n  d n  的前n项和T ． n 18．（12 分）记  A B C 的内角 A,B,C的对边分别为 a , b , c ，已知c=2acosAcosB−bcos2A (AB) ． （1）求A； （2）若D是 B C 乙类问题的概率为 0.5；C 员工能正确回答甲类问题的概率为 0.4，能正确回答乙类问题的概率 为0.75． （1）求3人得分之和为20分的概率； （2）设随机变量X为3人中得分为100的人数，求随机变量X的数学期望． 20．（12 分）已知四棱锥 上的一点，且BD:DC=1:2,AD=2，求a的最小值． 19．（12分）某单位组织知识竞赛，有甲、乙两类问题．现有A，B，C三位员工参加比赛，比赛规 则为：先从甲类问题中随机抽取一个问题回答，若回答错误则该员工比赛结束；若回答正确再从 乙类问题中随机抽取一个问题回答，无论回答正确与否，该员工比赛结束．每人两次回答问题的 过程相互独立．三人回答问题也相互独立．甲类问题中每个问题回答正确得20分，否则得0分； 乙类问题中每个问题回答正确得80分，否则得0分．已知A员工能正确回答甲类问题的概率为 0.5，能正确回答乙类问题的概率为 0.6；B 员工能正确回答甲类问题的概率为 0.6，能正确回答 S − A B C D 中，底面 A B C D 是矩形， 2 SA⊥BD,SA= AD= CD，M 是 2 S B 的中点． （1）证明： M C ⊥ B D ； （2）若 S A ⊥ A D , S A = 2 ，点 P 是 S C 上的动点，直线 A P 与平 面 A M C 所成角的正弦值为 1 1 0 0 ，求 S S P C ． x2 y2 21．（12分）已知椭圆C: + =1(b0)的左右焦点分别为F,F ，C是椭圆的中心，点M为 6 b2 1 2 其上的一点满足 MF  MF =5, MC =2． 1 2 （1）求椭圆C的方程； （2）设定点T(t,0) ，过点 T 的直线 l 交椭圆C于 P , Q 两点，若在C上存在一点 A ，使得直线 A P 的斜率与直线 A Q 的斜率之和为定值，求 t 的范围． lnx 22．（12分）已知函数 f (x)=eax −e −ea(x0)． x （1）当 a = 1 （第20题图） f (x) 时，求函数g(x)=eax−1− +x−a的单调区间； e （2）证明：当a−e−2时，不等式 f (x)0恒成立． {#{QQABCQqQogAgABIAAQhCQQVCCkCQkBEACAoGAFAAIAABwQFABAA=}#}中学生标准学术能力诊断性测试 2023 年 9 月测试 数学参考答案 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一 项是符合题目要求的． 1 2 3 4 5 6 7 8 B B B A C A C D 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项 符合题目要求．全部选对的得5分，部分选对但不全的得3分，有错选的得0分． 9 10 11 12 ABD ABD BCD ABC 三、填空题：本题共4小题，每小题5分，共20分． 24 13．− 14． 25 第1页 共6页 − 4 6 64 15． 16．1 3 四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分） n2 +n (n−1)2 +n−1 （1） S = ,S = ， n 2 n−1 2 S −S =n=c (n1,nN) ·································································· 2分 n n−1 n 又c =S =1,c =n ( nN+) ,a =3n ······················································· 3分 1 1 n n （2） d =3n ( 2n2 +6n+5 ) =(n+1)2 +13n+1− ( n2 +1 ) 3n ····························· 7分 n   T = ( 22 +1 ) 32 − ( 12 +1 ) 3+ ( 32 +1 ) 33− ( 22 +1 ) 32 + + n ( n2 +1 ) 3n −(n−1)2 +13n−1+(n+1)2 +13n+1− ( n2 +1 ) 3n     =− ( 12 +1 ) 3+(n+1)2 +13n+1   = ( n2 +2n+2 ) 3n+1−6 ····································································· 10分 18．（12分） （1） c=2acosAcosB−bcos2A(AB) ， {#{QQABCQqQogAgABIAAQhCQQVCCkCQkBEACAoGAFAAIAABwQFABAA=}#}sinC=2sinAcosAcosB−sinBcos2A ···················································· 2分 sinC=sin2AcosB−sinBcos2A=sin(2A−B)0 ··································· 4分 又 第2页 共6页 0  2 A − B   ，则C =2A−B或 C + 2 A − B =  ， 若 C = 2 A − B  ，则A= ； 3 若 C + 2 A − B =  ，则 A = 2 B ，又 A  B ，不符合题意，舍去，  综上所述A= ························································································· 6分 3 2 2AB+ AC ( )2 2AB+ AC （2） 2BD= DC,AD= , AD =  ···························· 8分 3 3   b2+4c2+2bc=36 ①，又 a 2 = b 2 + c 2 − b c ②， ①  2 c c 4 +2 +1     36 4c2 +b2 +2bc b b ②得： = = ········································ 9分 a2 b2 +c2 −bc c 2 c − +1     b b c 令 = x，又AB,ab,a2 b2,b2 +c2 −bcb2， b c cb,0 = x1， b 4x2 +2x+1 6x−3 令 f (x)= (0 x1), f (x)=4+ ······························ 10分 x2 −x+1 x2 −x+1 t+3 令6x−3=t,x= ， 6 36t 36  f (t)=4+ (−3t 3), f (t)=4+ (−3t 3) t2 +27 27 ， t+ t 27 27 36 6 7 又t+ 12或t+ −12,1 f (t)7, 7,a ， t t a2 7 6 7 所以当三角形ABC为等边三角形时a最小，最小值为 ····························· 12分 7 19．（12分） （1）设事件 A 1 为A员工答对甲类问题；设事件A 为A员工答对乙类问题； 2 设事件B 为B员工答对甲类问题；设事件B 为B员工答对乙类问题； 1 2 {#{QQABCQqQogAgABIAAQhCQQVCCkCQkBEACAoGAFAAIAABwQFABAA=}#}设事件 第3页 共6页 C 1 为C员工答对甲类问题；设事件 C 2 为C员工答对乙类问题； 三人得分之和为20分的情况有： ①A员工答对甲类题，答错乙类题；B与C员工均答错甲类题， 则P ( A A B C ) =P(A )P ( A ) P ( B ) P ( C ) =0.50.40.40.6=0.048 1 2 1 1 1 2 1 1 ·············································································································· 2分 ②B员工答对甲类题，答错乙类题；A与C员工均答错甲类题， P ( B B A C ) =P(B )P ( B ) P ( A ) P ( C ) =0.60.50.50.6=0.09 1 2 1 1 1 2 1 1 ·············································································································· 4分 ③C员工答对甲类题，答错乙类题；A与B员工均答错甲类题， P ( C C A B ) =P(C )P ( C ) P ( A ) P ( B ) =0.40.250.50.4=0.02， 1 2 1 1 1 2 1 1 所以三人得分之和为20分的概率为0.048+0.09+0.02=0.158 ·································· 6分 （2） A员工得100分的概率为P(A A )=P(A)P(A )=0.3， 1 2 1 2 B员工得100分的概率为P(B B )=P(B )P(B )=0.3， 1 2 1 2 C员工得100分的概率为P(C C )=P(C )P(C )=0.3， 1 2 1 2 ·············································································································· 9分 X ~ B(3,0.3) ······················································································ 11分  E(X)=30.3=0.9 ············································································ 12分 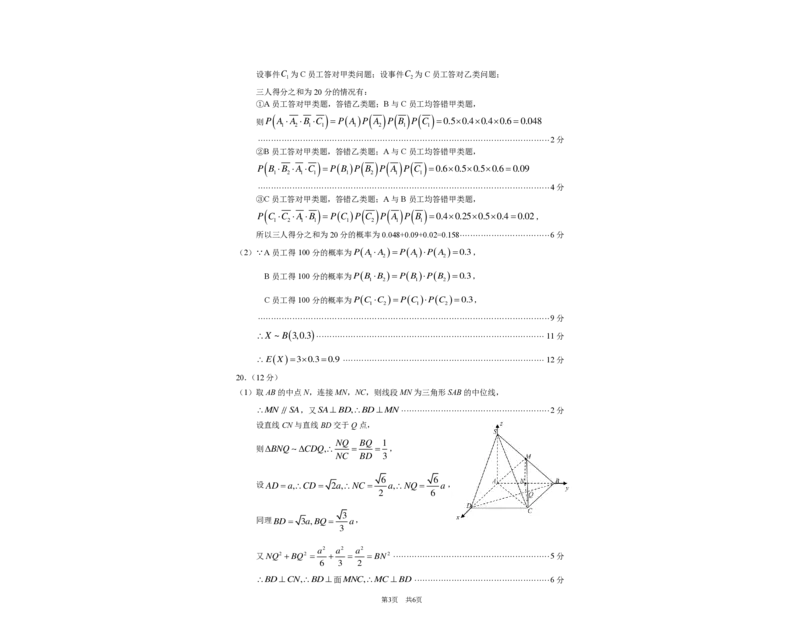20．（12分） （1）取AB的中点N，连接MN，NC，则线段MN为三角形SAB的中位线， MN SA，又SA⊥BD,BD⊥MN ························································ 2分 设直线CN与直线BD交于Q点， NQ BQ 1 则BNQ CDQ, = = ， NC BD 3 6 6 设AD=a,CD= 2a,NC = a,NQ= a， 2 6 3 同理BD= 3a,BQ= a， 3 a2 a2 a2 又NQ2 +BQ2 = + = = BN2 ··························································· 5分 6 3 2 BD⊥CN,BD⊥面MNC,MC⊥BD ··················································· 6分 {#{QQABCQqQogAgABIAAQhCQQVCCkCQkBEACAoGAFAAIAABwQFABAA=}#}（2）分别以直线AD，AB，AS为x轴，y轴，z轴建立直角坐标系， ( ) ( ) ( ) 则A(0,0,0),S(0,0,2),C 2,2 2,0 ,B 0,2 2,0 ,M 0, 2,1 ， 设 第4页 共6页 S P S C  = ， ( ) ( ) P 2,2 2,2(1−) ,AP= 2,2 2,2(1−) ································· 8分 ( ) ( ) 又AM = 0, 2,1 ,AC = 2,2 2,0 ， 设平面AMC的法向量 n = ( x , y , z ) ，  nAM = 2y+z =0 ( ) 则 ,n= − 2,1,− 2 ·········································· 10分 nAC =2x+2 2y =0 设直线AP与平面AMC所成的角为， 2 2(1−) 10 则sin= cos AP,n = = ， 5 162 −8+4 10 1 SP 1 = , = ·················································································· 12分 2 SC 2 21．（12分） （1）设 MF =r, MF =r ，在 1 1 2 2  M F 1 F 2 中，设FMF =， 1 2 FF 2 =r2 +r2 −2rr cos=4c2， 1 2 1 2 1 2 1( ) 2rr cos=r2 +r2 −4c2，又MC = MF +MF ， 1 2 1 2 2 1 2 MC 2 = 1( MF 2 +MF 2 +2MF MF ) = 1 ( r2 +r2 +2rr cos ) = r 1 2 + r 2 2 −c2， 4 1 2 1 2 4 1 2 1 2 2 2 r2 r2 (r +r )2 −2rr MC2 = 1 + 2 −c2 = 1 2 1 2 −c2 =2a2 −c2 −5=4 ························· 3分 2 2 2 2a2 −c2 =9, a2 =6,c2 =3,b2 =3， x2 y2 所以椭圆C的方程为： + =1 ······························································· 4分 6 3 （2）设A(x ,y ),P(x,y ),Q(x ,y ) ，直线l的方程为x=y+t， 0 0 1 1 2 2 {#{QQABCQqQogAgABIAAQhCQQVCCkCQkBEACAoGAFAAIAABwQFABAA=}#}x2 y2   6 + 3 =1  ( 2 +2 ) y2 +2ty+t2 −6=0，  x=y+t 2t t2 −6 y + y =− ,y y = ,x =y +t,x =y +t， 1 2 2 +2 1 2 2 +2 1 1 2 2 4t 2t2 −62 x +x = ,x x = ································································ 7分 1 2 2 +2 1 2 2 +2 y −y y −y (y −y )(x −x )+(y −y )(x −x ) 设 0 1 + 0 2 = 0 1 0 2 0 2 0 1 x −x x −x (x −x )(x −x ) 0 1 0 2 0 1 0 2 2x y −y (x +x )+2y y +(t−x )(y + y ) = 0 0 0 1 2 1 2 0 1 2 x2 −(x +x )x +x x 0 1 2 0 1 2 2x y2 +(2tx −12)+4y (x −t) = 0 0 0 0 0 = p ( x2 −6 ) 2 +2(x −t)2 0 0 若p为常数，则2tx −12=0 ····································································· 10分 0 2x y 4y (x −t) 2y 即6=tx 0 ，而此时 ( x2 0 −6 0 ) = 2( 0 x − 0 t)2 = x − 0 t ， 0 0 0 6 又− 6  x  6,− 6   6，即t  6或 0 t 第5页 共6页 t  − 6 ， 综上所述， t  6 或 t  − 6 6 18 ，存在点A , 3− ，使得直线AP的斜率与直线AQ  t t2    2y 的斜率之和为定值 0 ············································································ 12分 x −t 0 22．（12分） lnx (1−lnx) 1−lnx+x2 （1）g(x)= +x,g(x)= +1= ······································ 1分 x x2 x2 1 2 令h(x)=1−lnx+x2,h(x)=− +2x0，即x ， x 2  2   2  所以函数h(x) 在区间 ,+单调递增，在区间0, 单调递减 ················· 3分     2 2     {#{QQABCQqQogAgABIAAQhCQQVCCkCQkBEACAoGAFAAIAABwQFABAA=}#} 2  又h (x)=h 0,h(x)0,g(x)0， min  2    所以函数g(x) 在 (0,+) 上单调递增 ····························································· 5分 lnx （2）不等式eax −e −ea0等价于 x 第6页 共6页 x e a x − 1 − l n x − a x  0 1 令g(x)= xeax−1−lnx−ax0，g(x)= (1+ax)( xeax−1−1 ) ···························· 7分 x 设h(x)=xeax−1−1,h(x)=(ax+1)eax−1， 1 当0 x− ,h(x)0， a 所以函数 h ( x )  1 在 0,− 上单调递增，在  a  − 1 a , +   上单调递减， h (x)=h   − 1  =− 1 ( e−2 +a ) ， max  a a 1 a−e−2,h =− ( e−2 +a ) 0， max a 所以函数 g ( x )  1  在 − ,+ 单调递增，在  a   0 , − 1 a  单调递减 ··························· 10分  1 1 −1 g (x)= g  −  =− e−2 −ln −1， min  a a e2a −1 1 令 =t，则g (t)=t−lnt−1=m(t)( t(0,1)) ,m(t)=1− ， e2a min t m(t) 在 (0,1) 单调递减，在 (1,+) 单调递增， m (x)=m(1)=0,m(t)0， min g (x)0,g(x)0 ········································································ 12分 min 即a−e−2时，不等式 f (x)0恒成立． {#{QQABCQqQogAgABIAAQhCQQVCCkCQkBEACAoGAFAAIAABwQFABAA=}#}