文档内容
2024年高考押题预测卷
数学·全解全析
一、单选题
1.已知集合 , ,则 ( )
A. B. C. D.
【答案】C
【解析】由题意,得 , ,
所以 ,所以 .故选:C.
2.已知复数 满足 ,则复数 的共轭复数的模 ( )
A. B. C. D.
【答案】A
【解析】 ,
所以 ,所以 .故选:A.
3.设 是两个平面, 是三条直线,则下列命题为真命题的是( )
A.若 , , ,则
B.若 , ,则
C.若 , , ,则
D.若 , , ,则
【答案】D
1
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司【解析】对于A,若 , , ,则 相交或平行,故A错误;
对于B,若 , ,则 或 ,故B错误.
对于C,若 , , ,
当 两两相交时, 两两相交,故C错误;
对于D,若 , , ,由线面平行的性质可得 ,故D正确故选:D.
4.将8个数学竞赛名额全部分给4个不同的班,其中甲、乙两班至少各有1个名额,则不同的分配方案种
数为( )
A.56 B.84 C.126 D.210
【答案】B
【解析】将8个数学竞赛名额全部分给4个不同的班,其中甲、乙两班至少各有1个名额的分法,
等价于将 10个数学竞赛名额全部分给4个不同的班,每个班至少有1个名额的分法.
用3个隔板插入10个小球中间的空隙中,将球分成4堆,
由于 10个小球中间共有 9个空隙,因此共有 种不同的分法.故选:B.
5.记 为等比数列 的前 项和,若 ,则 ( )
A. B. C. D.
【答案】C
【解析】根据题意,设等比数列 的公比为 ,
若 ,即 ,故 .故选:C.
6. 的内角 的对边分别为 .已知 , , ,则 的外接圆半径为
( )
A. B. C. D.
2
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司【答案】A
【解析】因为 , , ,所以由余弦定理可得 ,
所以 ,设 的外接圆半径为 ,
由正弦定理可得 ,即 .
则 的外接圆半径为 .故选:A
7.己知 , ,则 ( )
A. B. C. D.
【答案】B
【解析】因为 ,
所以 ,所以 ,
所以 ,所以 ,
因为 ,所以 ,
所以 ,所以 ,所以 .故选:B.
8.双曲线 的左、右顶点分别为 , ,左、右焦点分别为 , ,过 作直线与双曲线
的左、右两支分别交于 , 两点.若 ,且 ,则直线 与 的斜率之积
为( )
3
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司A. B. C. D.
【答案】D
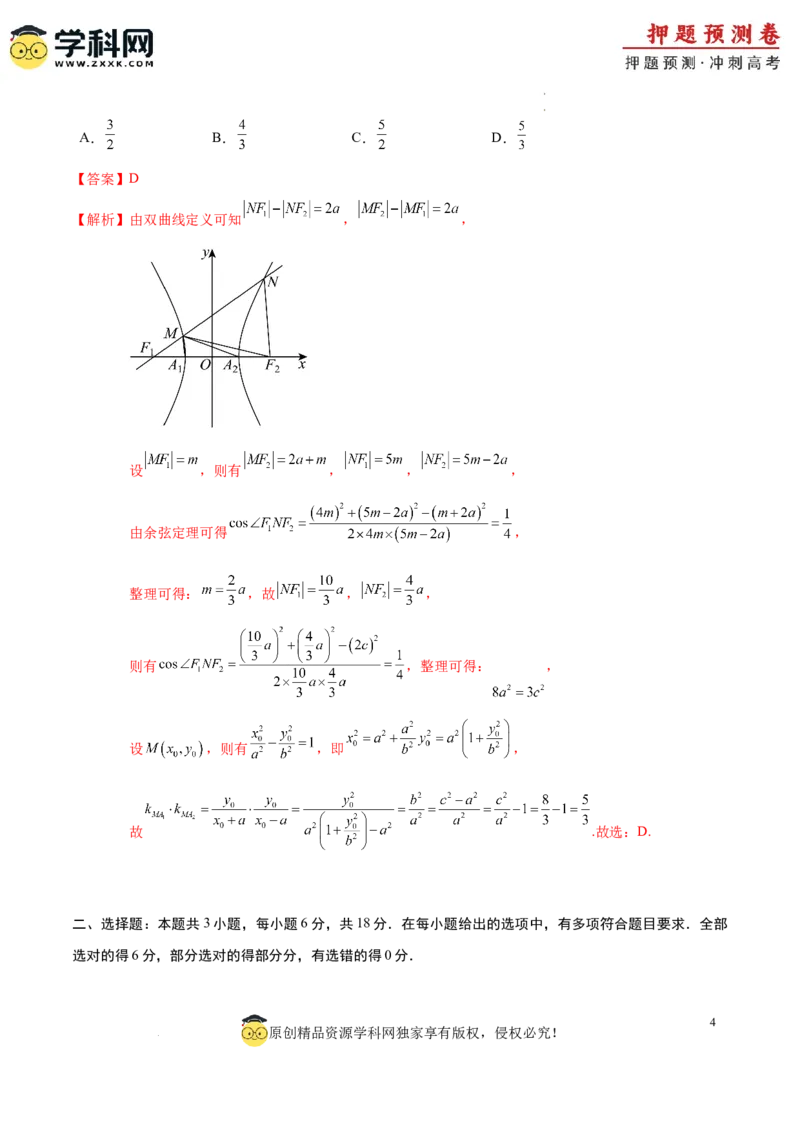
【解析】由双曲线定义可知 , ,
设 ,则有 , , ,
由余弦定理可得 ,
整理可得: ,故 , ,
则有 ,整理可得: ,
设 ,则有 ,即 ,
故 .故选:D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
4
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司9.若 是样本数据 的平均数,则( )
A. 的极差等于 的极差
B. 的平均数等于 的平均数
C. 的中位数等于 的中位数
D. 的标准差大于 的标准差
【答案】AB
【解析】对于A,样本数据 的平均数为 ,则 ,
故 的极差等于 的极差,故A正确;
对于B,数据 的平均数 ,故B正确;
对于C,如果 是按从小到大排列,
则 的中位数为 ,不一定等于 的中位数,故C错误;
对于D, 的方差 ,
而 的方差 ,
但当 时两组数据的方差相等,其标准差也相等,故D错误.故选:AB.
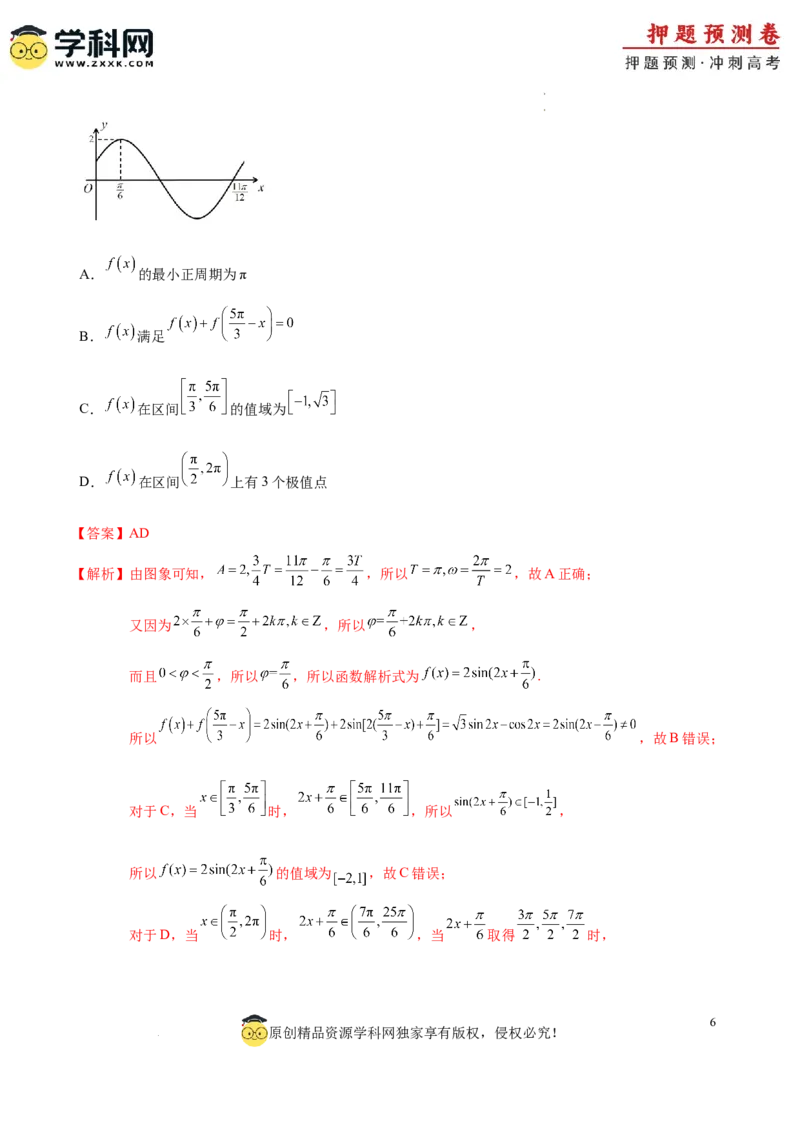
10.已知 的部分图象如图所示,则( )
5
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司A. 的最小正周期为π
B. 满足
C. 在区间 的值域为
D. 在区间 上有3个极值点
【答案】AD
【解析】由图象可知, ,所以 ,故A正确;
又因为 ,所以 ,
而且 ,所以 ,所以函数解析式为 .
所以 ,故B错误;
对于C,当 时, ,所以 ,
所以 的值域为 ,故C错误;
对于D,当 时, ,当 取得 时,
6
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司取得极值,所以 在 上有3个极值点,故D正确.故选:AD.
11.已知函数 的定义域为 ,其导函数为 ,若函数 的图象关于点 对称,
,且 ,则( )
A. 的图像关于点 对称 B.
C. D.
【答案】ACD
【解析】对于A中,设函数 的图象关于 对称,
则 关于 对称,可得 关于 对称,
因为函数 的图像关于点 对称,可得 ,解得 ,
所以函数 的图象关于 对称,所以A正确;
对于B中,由函数 的图象关于 对称,可得 ,
因为 ,可得 ,
则 ,
两式相减得 ,即 ,所以B不正确;
对于C中,令 ,可得 ,
因为 ,所以 ,所以函数 是以4为周期的周期函数,
由 ,可得 ,所以 ,
7
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司因为函数 是以4为周期的周期函数,则 是以4为周期的周期函数,
所以 ,
由 ,可得 ,
即 ,令 ,可得 ,所以 ,
所以 ,所以 ,所以C正确;
对于D中,因为 ,且函数 关于 对称,可得 ,
又因为 ,令 ,可得 ,所以 ,
再令 ,可得 ,所以 ,
由 ,可得 ,
可得
又由函数 是以4为周期的周期函数,且 ,
所以
,所以D正确.故选:ACD.
第二部分(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分。
12. 的展开式中常数项为 .
【答案】16
8
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司【解析】依题意, 展开式的常数项为 ,
含 的项为 ,
所以 的展开式中常数项为 .
13.若抛物线 的焦点到直线 的距离为1,则实数 的值为 .
【答案】
【解析】由抛物线 可化为 ,可得其焦点为 ,
因为抛物线 的焦点到直线 的距离为 ,
可得 ,解得 或 (舍去),故实数 的值为 .
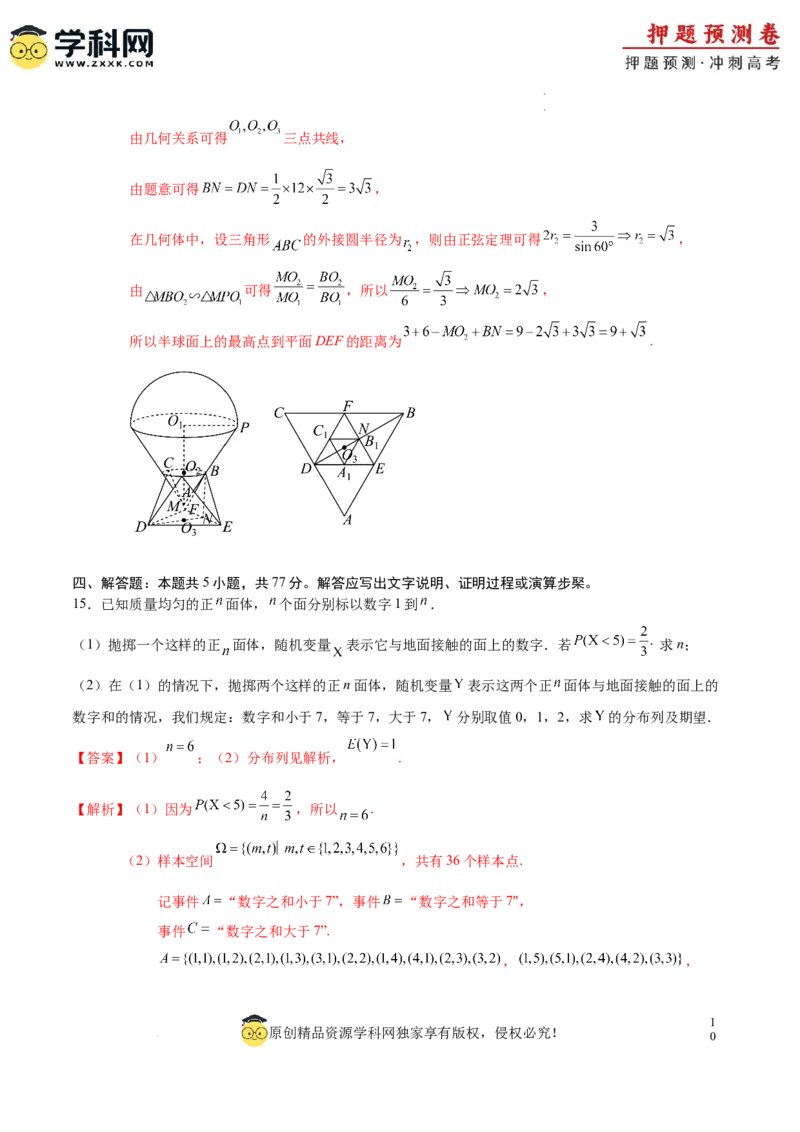
14.某冰淇淋门面店将上半部是半球(半球的半径为3),下半部是倒立的圆锥(圆锥的高为6)的冰淇淋
模型放到椐窗内展览,托盘是边长为12的等边三角形ABC金属片沿三边中点D,E,F的连线向上折叠成
直二面角而成,则半球面上的最高点到平面DEF的距离为 .
【答案】
【解析】设上面球心为 , 的圆心为 , 三点在底面投影的正三角形 的中心为 ,
圆锥的顶点为 , 边中点为 ,
连接 ,由题意可知 , ,
9
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司由几何关系可得 三点共线,
由题意可得 ,
在几何体中,设三角形 的外接圆半径为 ,则由正弦定理可得 ,
由 可得 ,所以 ,
所以半球面上的最高点到平面DEF的距离为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.已知质量均匀的正 面体, 个面分别标以数字1到 .
(1)抛掷一个这样的正 面体,随机变量 表示它与地面接触的面上的数字.若 求n;
(2)在(1)的情况下,抛掷两个这样的正n面体,随机变量 表示这两个正 面体与地面接触的面上的
数字和的情况,我们规定:数字和小于7,等于7,大于7, 分别取值0,1,2,求 的分布列及期望.
【答案】(1) ;(2)分布列见解析, .
【解析】(1)因为 ,所以 .
(2)样本空间 ,共有36个样本点.
记事件 “数字之和小于7”,事件 “数字之和等于7",
事件 “数字之和大于7”.
, ,
1
原创精品资源学科网独家享有版权,侵权必究!
0
学学科科网网((北北京京))股股份份有有限限公公司司共15种,故
,共6种,
故 ;
,
,共15种,故 ;
从而 的分布列为:
0 1 2
故
16.已知函数 .
(1)若 的图象在点 处的切线与直线 垂直,求 的值;
(2)讨论 的单调性与极值.
【答案】(1) ;(2)答案见解析.
【解析】(1)由题得, 的定义域为 .
.
的图象在点 处的切线与直线l:2x 垂直,
,解得 .
(2)由(1)知 .
1
原创精品资源学科网独家享有版权,侵权必究!
1
学学科科网网((北北京京))股股份份有有限限公公司司①当 时, 恒成立, 在 上为减函数,此时 无极值;
②当 时,由 ,得 ,由 ,得 ,
在 上单调递减,在 上单调递增,
故 的极小值为 .
综上可得,当 时, 在 上为减函数, 无极值;
当 时, 在 上单调递减,在 上单调递增.
的极小值为 ,无极大值.
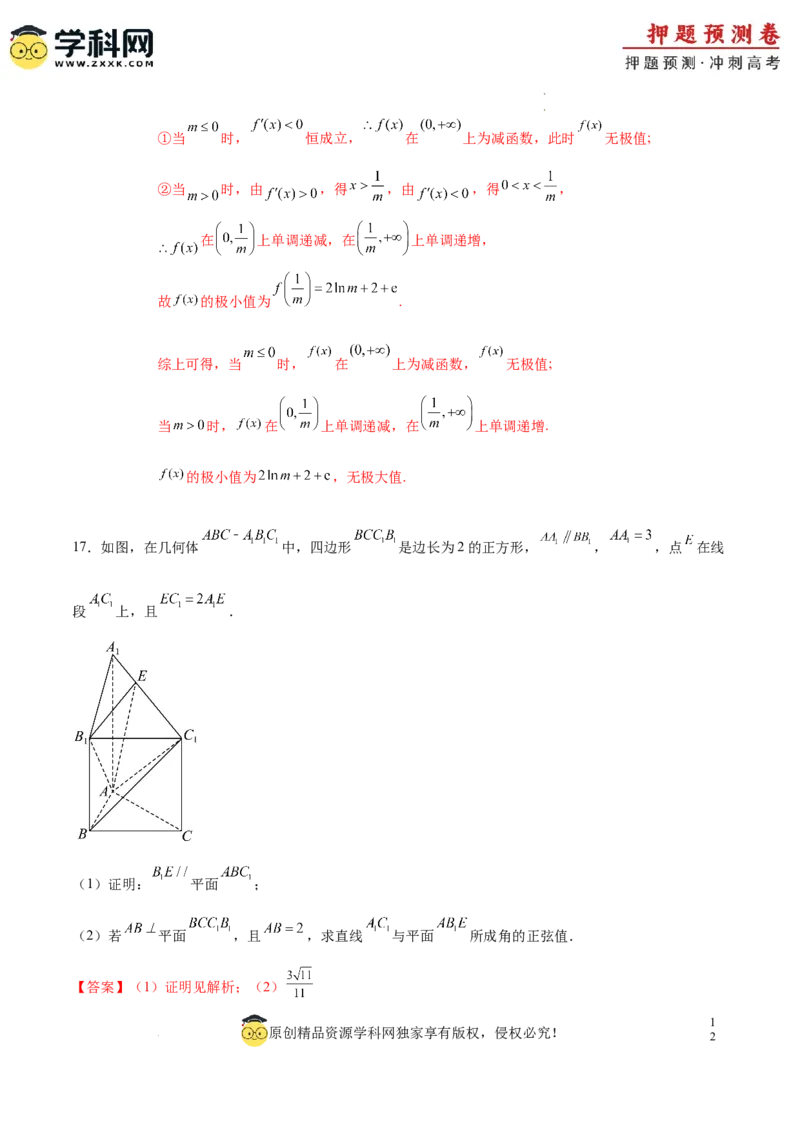
17.如图,在几何体 中,四边形 是边长为2的正方形, , ,点 在线
段 上,且 .
(1)证明: 平面 ;
(2)若 平面 ,且 ,求直线 与平面 所成角的正弦值.
【答案】(1)证明见解析;(2)
1
原创精品资源学科网独家享有版权,侵权必究!
2
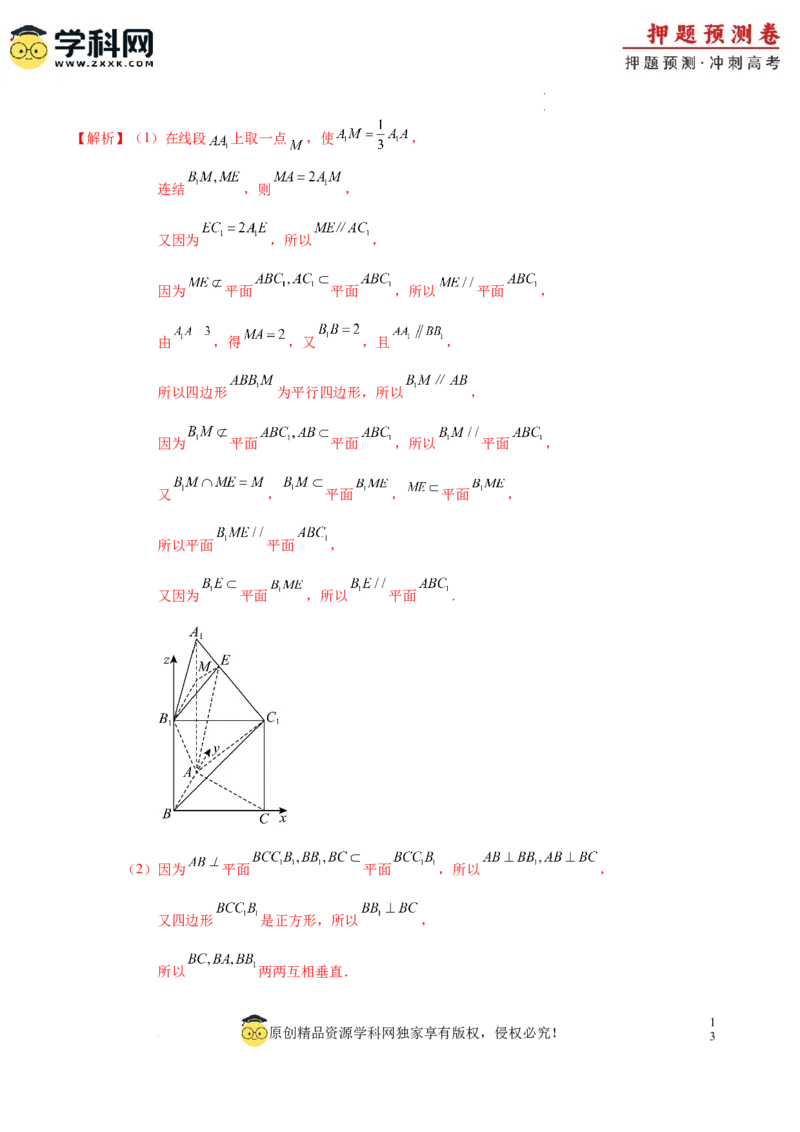
学学科科网网((北北京京))股股份份有有限限公公司司【解析】(1)在线段 上取一点 ,使 ,
连结 ,则 ,
又因为 ,所以 ,
因为 平面 平面 ,所以 平面 ,
由 ,得 ,又 ,且 ,
所以四边形 为平行四边形,所以 ,
因为 平面 平面 ,所以 平面 ,
又 , 平面 , 平面 ,
所以平面 平面 ,
又因为 平面 ,所以 平面 .
(2)因为 平面 平面 ,所以 ,
又四边形 是正方形,所以 ,
所以 两两互相垂直.
1
原创精品资源学科网独家享有版权,侵权必究!
3
学学科科网网((北北京京))股股份份有有限限公公司司所以以 为原点,以 所在直线分别为 轴, 轴, 轴,
建立如图所示的空间直角坐标系,
由 ,得 ,
于是 , ,
设平面 的法向量为 ,则 ,
得 ,即 ,
令 ,得 ,所以平面 的一个法向量 ,
设直线 与平面 所成的角为 ,
则 ,
所以直线 与平面 所成角的正弦值为 .
18.已知O为坐标原点,椭圆C: 的上、下顶点为A、B,椭圆上的点P位于第二象限,
直线PA、PB、PO的斜率分别为 ,且 .
(1)求椭圆C的标准方程;
(2)过原点O分别作直线PA、PB的平行线与椭圆相交,得到四个交点,将这四个交点依次连接构成一个
四边形,则此四边形的面积是否为定值?若为定值,请求出该定值;否则,请求出其取值范围.
【答案】(1) ;(2)是定值,
1
原创精品资源学科网独家享有版权,侵权必究!
4
学学科科网网((北北京京))股股份份有有限限公公司司【解析】(1)由题意可得 ,
设 ,则 ,
∵ ,∴ ,化简得: ①,
又 在椭圆上, ②,
由①②得 ,
又 ,∴ ,故椭圆C的标准方程 ;
(2)设直线 的平行线与椭圆相交于点 、 ( 在上方),
直线 的平行线与椭圆相交于点 、 ( 在上方),
∴直线 的方程为 ,直线 的方程为 ,
又 ,∴ ,
联立 ,解得 ,∴ ,
联立 ,解得 ,∴ ,
设直线EF的倾斜角为 ,直线GH的倾斜角为 , ,
∴ ,
则 ,
1
原创精品资源学科网独家享有版权,侵权必究!
5
学学科科网网((北北京京))股股份份有有限限公公司司,
∴四边形面积为:
,
故该四边形的面积为定值 .
19.已知 ,集合 其中 .
(1)求 中最小的元素;
(2)设 , ,且 ,求 的值;
(3)记 , ,若集合 中的元素个数为 ,求 .
【答案】(1)7;(2) 或10;(3)
【解析】(1) 中的最小元素为 .
(2)由题得 ,设 , .
①当 时, 或 或
或 或 或 .
1
原创精品资源学科网独家享有版权,侵权必究!
6
学学科科网网((北北京京))股股份份有有限限公公司司经检验,当 时, ,符合题意,所以 .
②当 时, 或 或 或 .
经检验,当 时, ,符合题意,所以 .
③当 时,不符合题意.因此, 或10.
(3)设 ,则 ,其中 ,
,所以 ,
设 ,则 .
因为 ,
所以
.
因为 ,
所以 ,所以 ,
又因为 ,所以 .
1
原创精品资源学科网独家享有版权,侵权必究!
7
学学科科网网((北北京京))股股份份有有限限公公司司