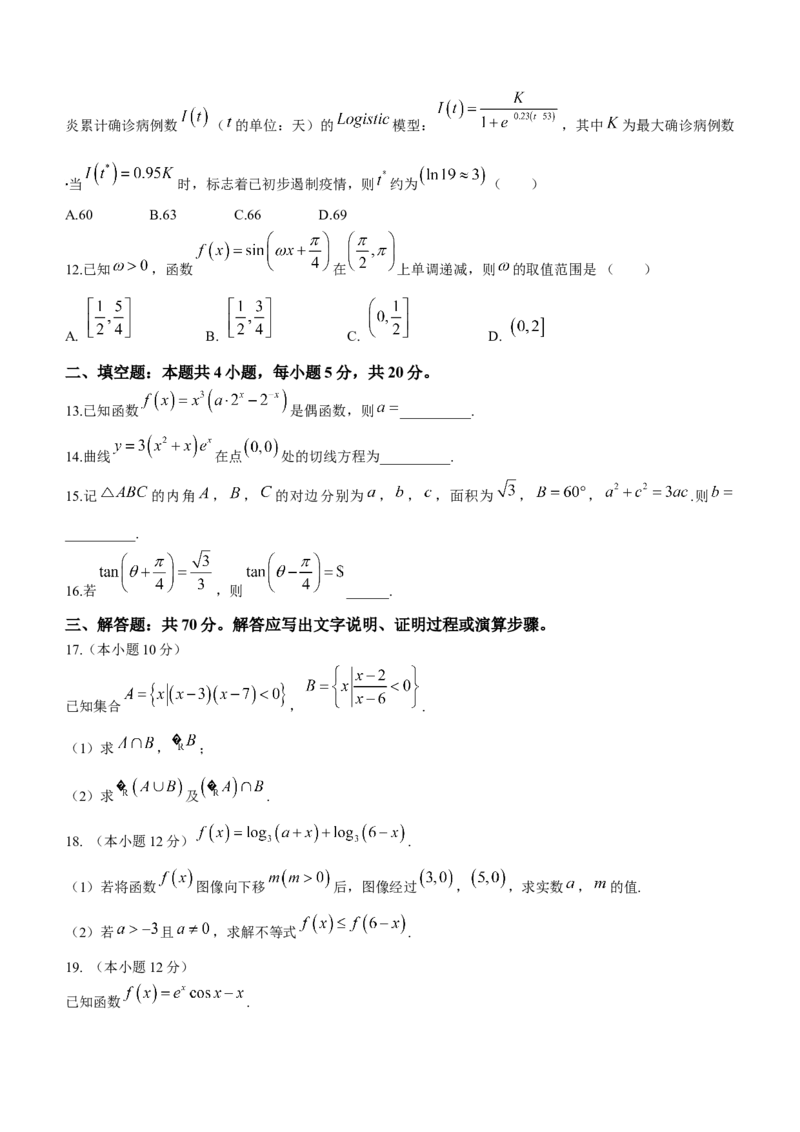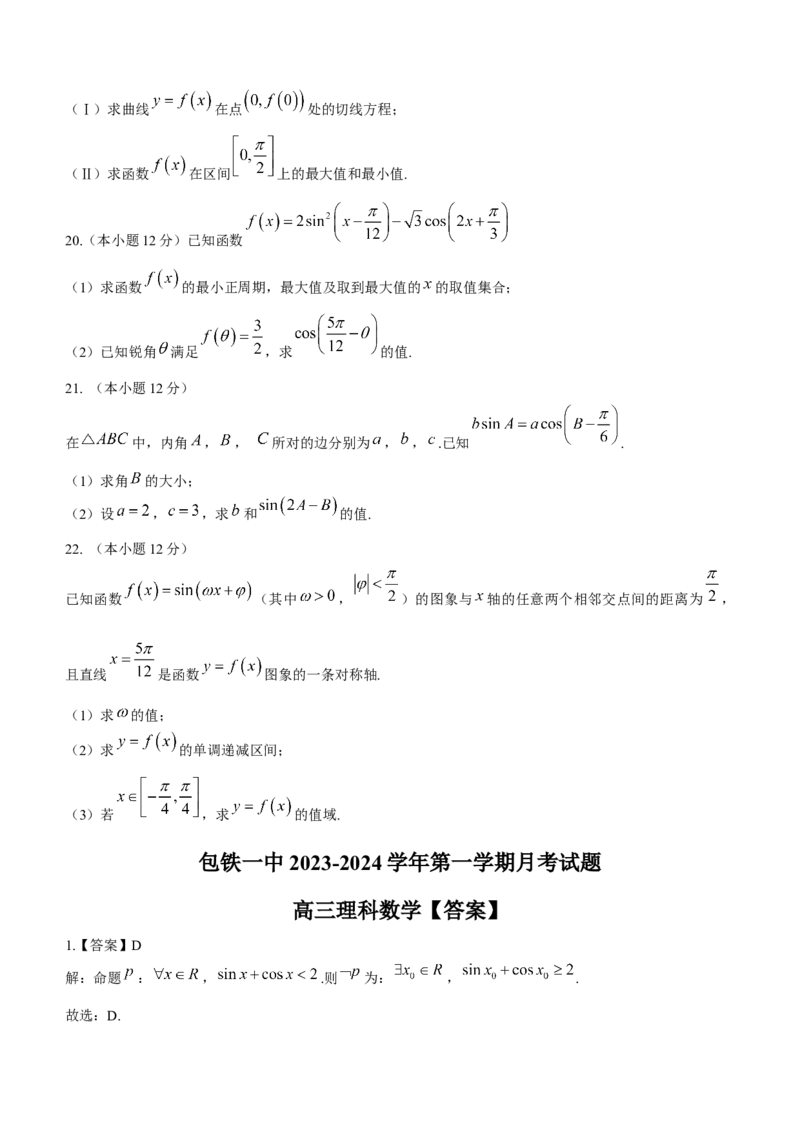文档内容
包铁一中 2023-2024 学年第一学期月考试题
高三理科数学
本试卷共22题,共150分,共4页(不含答题卡)。考试时间120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填涂在答题卡上。
2.作答时,务必将答案写在答题卡上各题目的规定区域内,写在本试卷及草稿纸上无效。
3.考试结束后,答题卡交回,试卷自行留存。
4.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.已知集合 , ,则 ( )
A. B. C. D.
2.下列函数中,在区间 上单调递增的是( )
A. B. C. D.
3.已知命题 : , ;命题 : , ,则下列命题中为真命题的是( )
A. B. C. D.
4. ( )
A. B. C. D.
5.已知函数 ,在下列区间中,包含 零点的区间是( )
A. B. C. D.
6. 的内角 , , 的对边分别为 , , .若 的面积为 ,则 ( )
A. B. C. D.
学科网(北京)股份有限公司7.设 , , ,则三者大小关系为( )
A. B. C. D.
8.函数 的图象可能是( )
A. B.
C. D.
9.下列函数中,其图象与函数 的图象关于直线 对称的是( )
A. B.
C. D.
10.函数 的部分图象如图所示,则 的单调递减区间为( )
A. , B. ,
C. , D. ,
11. 模型是常用数学模型之一,可应用于流行病学领域,有学者根据公布数据建立了某地区新冠肺
学科网(北京)股份有限公司炎累计确诊病例数 ( 的单位:天)的 模型: ,其中 为最大确诊病例数
当 时,标志着已初步遏制疫情,则 约为 ( )
A.60 B.63 C.66 D.69
12.已知 ,函数 在 上单调递减,则 的取值范围是( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分。
13.已知函数 是偶函数,则 __________.
14.曲线 在点 处的切线方程为__________.
15.记 的内角 , , 的对边分别为 , , ,面积为 , , .则
__________.
16.若 ,则 ______.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题10分)
已知集合 , .
(1)求 , ;
(2)求 及 .
18. (本小题12分) .
(1)若将函数 图像向下移 后,图像经过 , ,求实数 , 的值.
(2)若 且 ,求解不等式 .
19. (本小题12分)
已知函数 .
学科网(北京)股份有限公司(Ⅰ)求曲线 在点 处的切线方程;
(Ⅱ)求函数 在区间 上的最大值和最小值.
20.(本小题12分)已知函数
(1)求函数 的最小正周期,最大值及取到最大值的 的取值集合;
(2)已知锐角 满足 ,求 的值.
21. (本小题12分)
在 中,内角 , , 所对的边分别为 , , .已知 .
(1)求角 的大小;
(2)设 , ,求 和 的值.
22. (本小题12分)
已知函数 (其中 , )的图象与 轴的任意两个相邻交点间的距离为 ,
且直线 是函数 图象的一条对称轴.
(1)求 的值;
(2)求 的单调递减区间;
(3)若 ,求 的值域.
包铁一中 2023-2024 学年第一学期月考试题
高三理科数学【答案】
1.【答案】D
解:命题 : , .则 为: , .
故选:D.
学科网(北京)股份有限公司2.【答案】A
解:方程 表示圆,所以 即 ,∴ ,解得 的取值范围是
.
故选:A.
3.【答案】D
解:互为逆否命题的两个命题是等价命题,“若 ,则 ”的逆否命题是“若 ,则
”.
故选D.
4.【答案】B
解:圆 ,即 的圆心为 ,半径为 ,
,∴圆C的半径为5-3=2,
∴圆C的标准方程为: ,即 .
故选B.
5.【答案】B
解: ,运用集合的知识易知,
A中 是p的充要条件;B中 是p的必要条件;
C中 是p的充分条件;D中 是p的既不充分也不必要条件.
应选B项.
6.【答案】B
解:根据题意,圆的圆心到直线的距离,就是半径,
则 .∴圆的方程为: .
故选:B.
7.【答案】B
解:圆 的圆心坐标为(0,0),半径为2,
∵圆心到直线 的距离为 ,∴弦 的长等于 .
故答案为 .
学科网(北京)股份有限公司故选:B.
8.【答案】A
解:依题意, 是正三角形,
因为在 中, , , ,
所以 ,即椭圆的离心率 ,
故选A.
9.【答案】C
解:椭圆 化为标准方程为: ,
∴离心率的平方 ,
∵椭圆 离心率的平方 ,
∴椭圆 和 具有相同的离心率.
故选 .
10.【答案】D
解:设圆的一般式方程为: ,
因为圆经过三点 , , 的坐标,
所以 ,
解得: , , ,
故圆的方程为: ,
学科网(北京)股份有限公司整理得: ,
所以 .
故选:D.
11.【答案】B
解:两圆方程作差得 ,
当 时,由 得 ,即 ,
即两圆的交点坐标为 , ,
则 ,
故选:B.
12.【答案】A
解:椭圆的焦点坐标为 ,
不妨设 ,可得 ,
解得 ,
椭圆的离心率为 .
故选A.
13.【答案】
解:圆的标准型为 ,
所以半径为,
故答案为:
换成标准型,求出半径.
本题考查圆的方程和性质,为基础题.
14.【答案】①④
解:因为 : , : ,
所以 假 真,
故①④正确.
学科网(北京)股份有限公司15.【答案】
解:方程 表示焦点在 轴上的椭圆,
则 ,解得 .
故答案为 .
16.【答案】
解:∵ ,∴焦点在 轴上
所以 , ,所以 2.
因为 ,所以 ,
所以 ,所以 .
故答案为 .
17.【答案】解: : , : .
因为 是 的必要不充分条件,所以 是 的充分不必要条件,
即 ,故有 或 ,
解得 .又 ,
所以实数m的取值范围为 .
18.【答案】解:将 化为标准方程为 ,
学科网(北京)股份有限公司即 ,所以 , , ,
因此顶点为 , ,
焦点为 , ,
实轴长 ,虚轴长 ,
离心率 ,
渐近线方程为 .
19.【答案】解:(1)由题意知 , , ,
焦点所在坐标轴可为x轴,也可为y轴,
故椭圆的标准方程为 或 .
(2)由 ,
设 , , ,则 .
又经过的点(2,0)为其顶点,
故若点(2,0)为长轴顶点,则 , ,
椭圆的标准方程为 ;
若点(2,0)为短轴顶点,
则 , ,椭圆的标准方程为 .
20.【答案】解:(1)由题意,圆心C为 的中点 ,
圆的直径为 ,
学科网(北京)股份有限公司∴圆的半径 ,
∴所求圆的方程为: ;
(或者写为一般方程: ).
(2)方法1.∵
∴令 ,则 ,化简得: .
∴ 或 ,
∴ 或 ,∴交点P的坐标为(1,0),(2,0).
方法2.∵ ,
令 ,则 ,
∴ 或 ,∴交点 的坐标为(1,0),(2,0).
21.【答案】解:(1)设圆 的圆心坐标为 ,半径为 ,
设圆 的方程为 ,且圆心 在直线 : 上,
由题意可得 ,
解得 ,
所以圆 方程为 ;
(2)因为直线 经过点 ,且被圆 截得的线段长为 ,
学科网(北京)股份有限公司∴圆心 到直线的距离为 ,
当直线 的斜率不存在时,此时圆心到直线的距离为3,不符合条件,
当直线 的斜率存在时,设直线 的方程为 ,
即 ,
则圆心 到直线 的距离为 ,
即 解得 或 ,
此时直线 的方程为 或 ,
综上所述直线 的方程为 或 .
22.【答案】解:(1)将 代入 ,
消去 ,整理得 .①
因为直线 与椭圆 相交于A,B两个不同的点,
所以 ,
解得 .
所以b的取值范围为 .
(2)设 , ,当 时,方程①为 .
解得 , .
相应地 , .
学科网(北京)股份有限公司所以 .
学科网(北京)股份有限公司