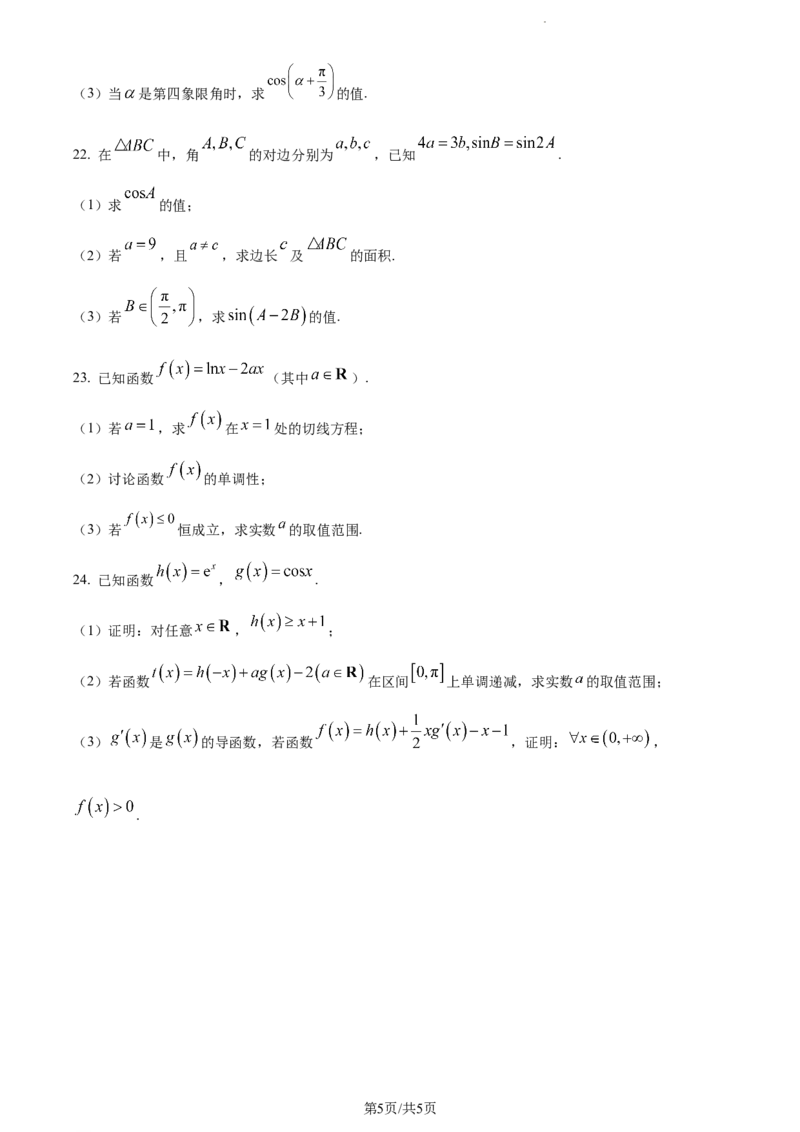文档内容
大港一中 2024 届高三年级第一次形成性检测
数学试卷
一、选择题:本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是
符合题目要求的,请将所选答案填入答题纸中的答题栏内.
1. 已知全集 ,集合 ,则集合 ( )
A. B. C. D.
2. 有一组样本数据如下:56,62,63,63,65,66,68,70,71,74,则其75%分位数为( )
A. 68 B. 69 C. 70 D. 71
3. 是函数 在 单调递减的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要
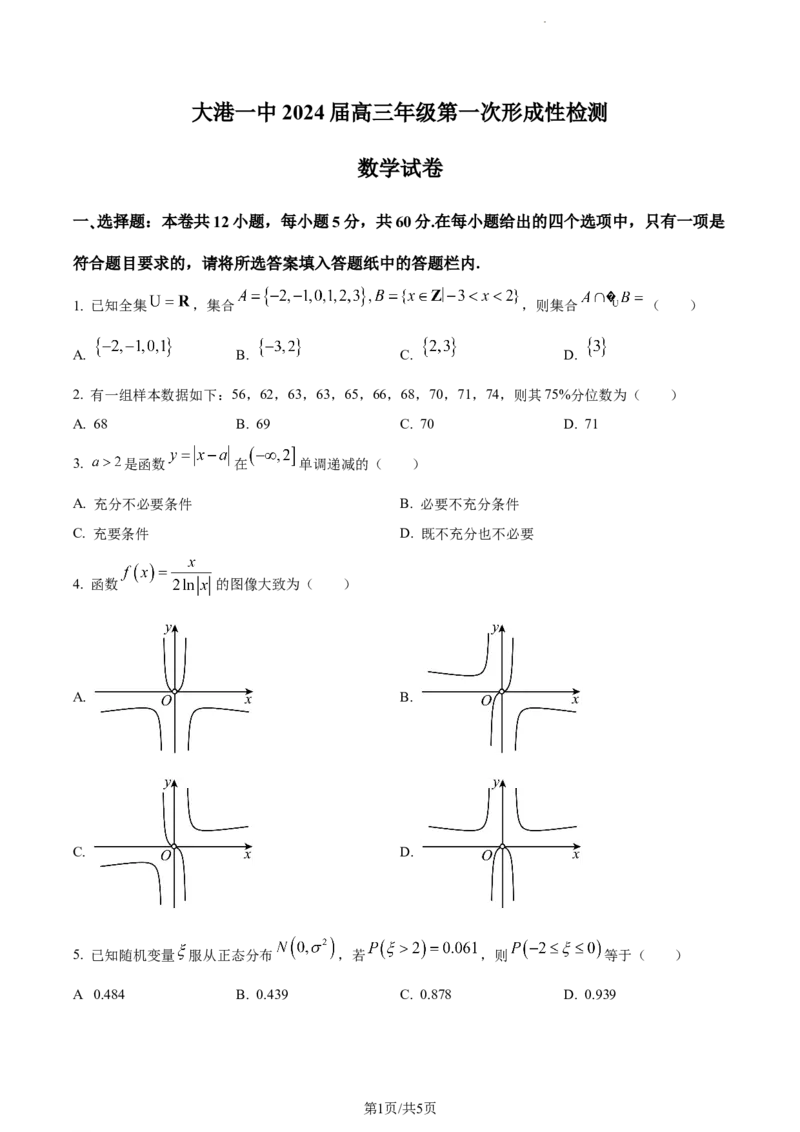
4. 函数 的图像大致为( )
A. B.
C. D.
5. 已知随机变量 服从正态分布 ,若 ,则 等于( )
.
A 0.484 B. 0.439 C. 0.878 D. 0.939
第1页/共5页
学科网(北京)股份有限公司6. 已知 ,则 的大小关系为( )
A. B.
C. D.
7. 为研究高中生爱好某项运动是否与性别有关,某校研究性学习小组采取简单随机抽样的方法调查了200
名高中生,依据独立性检验,经计算得到 ,参照下表,得到的正确结论是( )
P( ≥ ) 0.1 0.05 0.01 0.005 0.001
.
2.706 3.841 6635 7.879 10.828
A. 有99%的高中生爱好该项运动
B. 有99%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别无关”
8. 在 三个地区暴发了流感,这三个地区分别有 的人患了流感.假设这三个地区的人
口数的比为 ,现从这三个地区中任意选取一人,则这个人患流感的概率为( )
A. B. C. D.
9. 设函数 ,其中向量 , , ,则下列选项错误
的是( )
A. 直线 是函数 的一条对称轴
B. 点 是函数 的一个对称中心
C. 在区间 上单调递增
D. 图象上所有点的横坐标向左平移 个单位长度得到的函数是偶函数
第2页/共5页
学科网(北京)股份有限公司10. 设实数 满足 ,则 的最小值为( )
A. B. C. D.
11. 已知函数 有最大值,则实数 取值范围为( )
的
A. B. C. D.
12. 已知函数 (其中a∈R),若 的四个零点从小到大依次为
,则 的值是( )
A. 16 B. 13 C. 12 D. 10
二、填空题:本大题共8小题,每小题5分,共40分.
13. 是虚数单位,计算 __________.
14. 的展开式中, 的系数为__________.
.
15 __________.
16. 小明上学途中共有4个红绿灯,且小明遇到每个红灯的概率均为 ,记某次小明上学途中遇到红灯的
次数为 ,则小明上学途中恰好遇到两个红灯的概率为__________, __________.
17. 新冠肺炎疫情发生以来,中医药全面参与疫情防控救治,做出了重要贡献.某中医药企业根据市场调研
与模拟,得到研发投入 (亿元)与产品收益 (亿元)的数据统计如下表:
研发投入 (亿元) 1 2 3 4 5
产品收益 (亿 3 7 9 10 11
第3页/共5页
学科网(北京)股份有限公司元)
用最小二乘法求得 关于 的经验回归直线方程是 ,当研发投入 亿元时,相应的产品收益
估计值为__________.
18. 某校高三1班第一小组有男生4人,女生2人,为提高中学生对劳动教育重要性的认识,现需从中抽
取2人参加学校开展的劳动技能学习,恰有一名女生参加劳动学习的概率则为__________;在至少有一名
女生参加劳动学习的条件下,都是女生参加劳动学习的概率______________.
19. 设函数 (A, , 是常数, , ).若 在区间 上具
有单调性,且 ,则 ______.
20. 如 图 , 在 平 行 四 边 形 中 , , 点 分 别 在 边
上,且 ,若 点为 的中点,且满足 ,则
________;当 点在线段 上运动时, 的取值范围为________.
三、解答题:本大题共4小题,共50分.解答应写出文字说明,证明过程或演算步骤.
21. 已知 .
(1)求 的值;
(2)求 的值;
第4页/共5页
学科网(北京)股份有限公司(3)当 是第四象限角时,求 的值.
22. 在 中,角 的对边分别为 ,已知 .
(1)求 的值;
(2)若 ,且 ,求边长 及 的面积.
(3)若 ,求 的值.
23. 已知函数 (其中 ).
(1)若 ,求 在 处的切线方程;
(2)讨论函数 的单调性;
(3)若 恒成立,求实数 的取值范围.
24. 已知函数 , .
(1)证明:对任意 , ;
(2)若函数 在区间 上单调递减,求实数 的取值范围;
(3) 是 的导函数,若函数 ,证明: ,
.
第5页/共5页
学科网(北京)股份有限公司