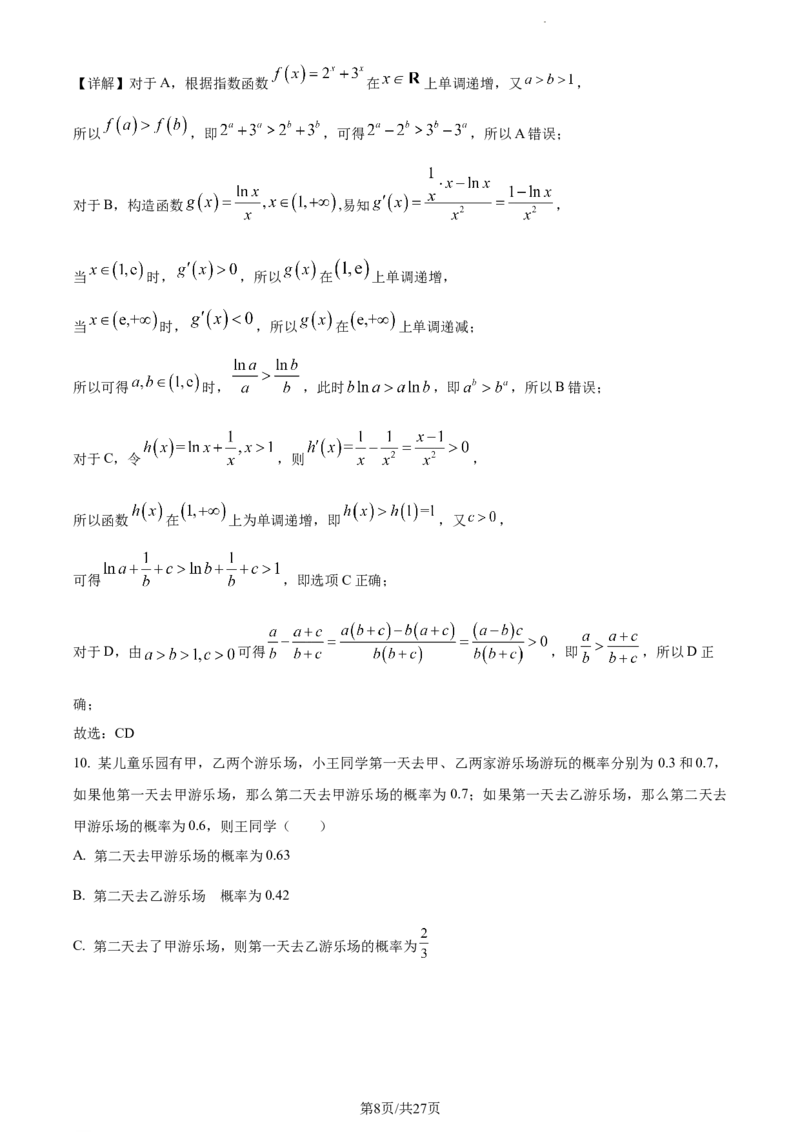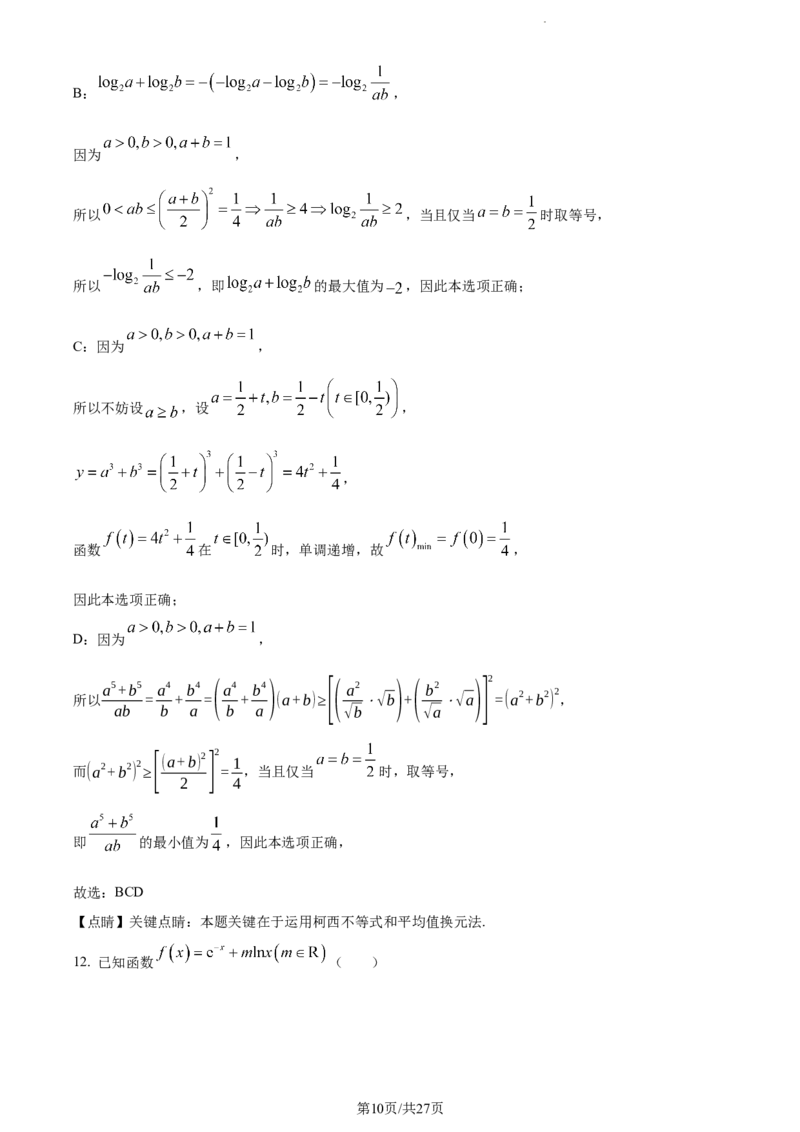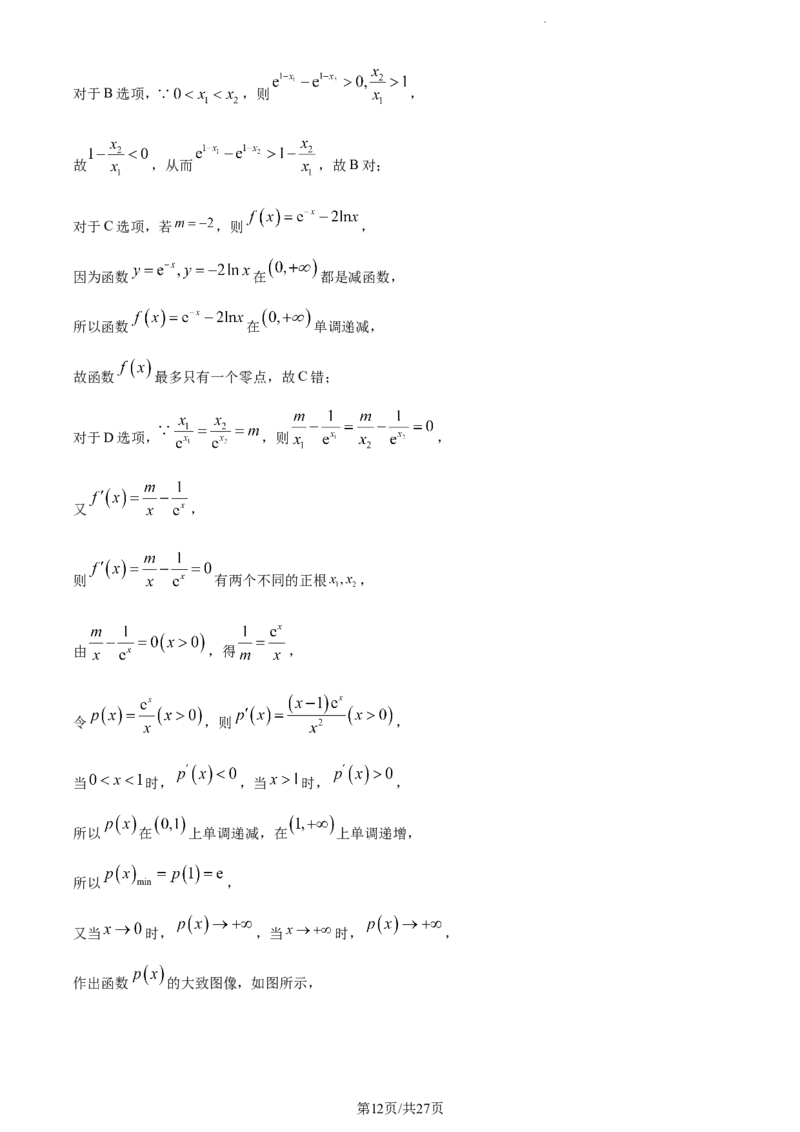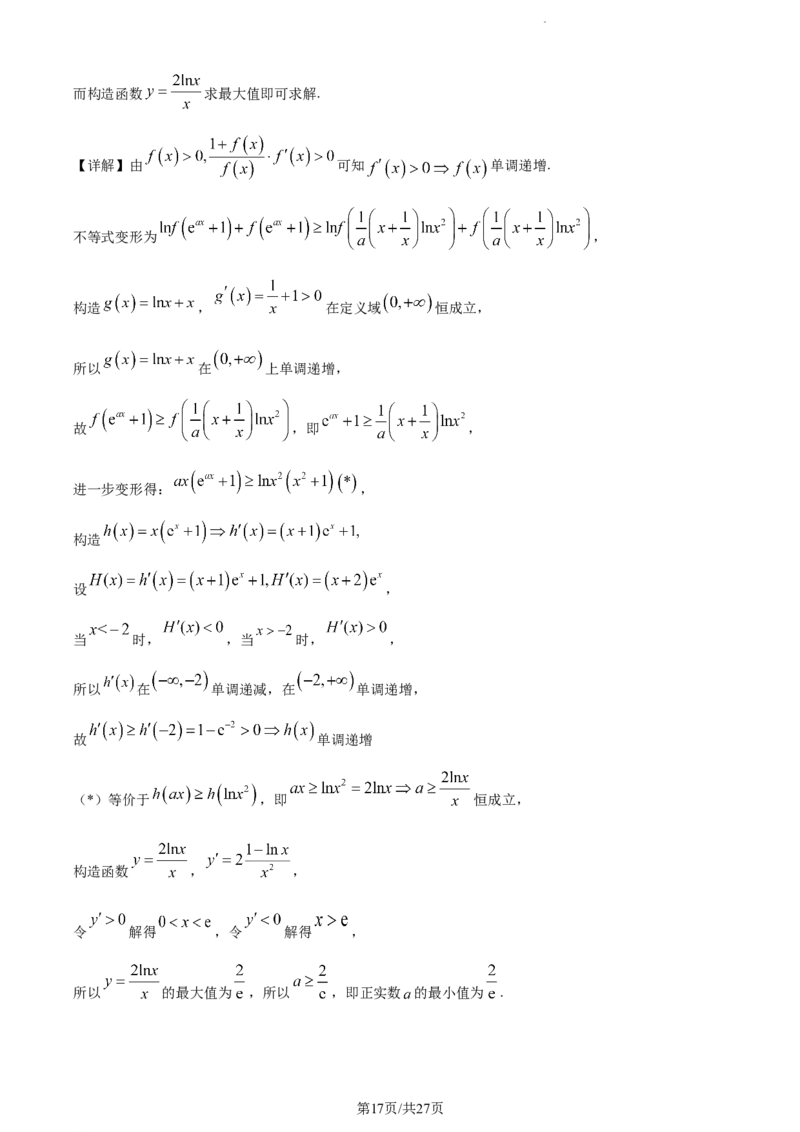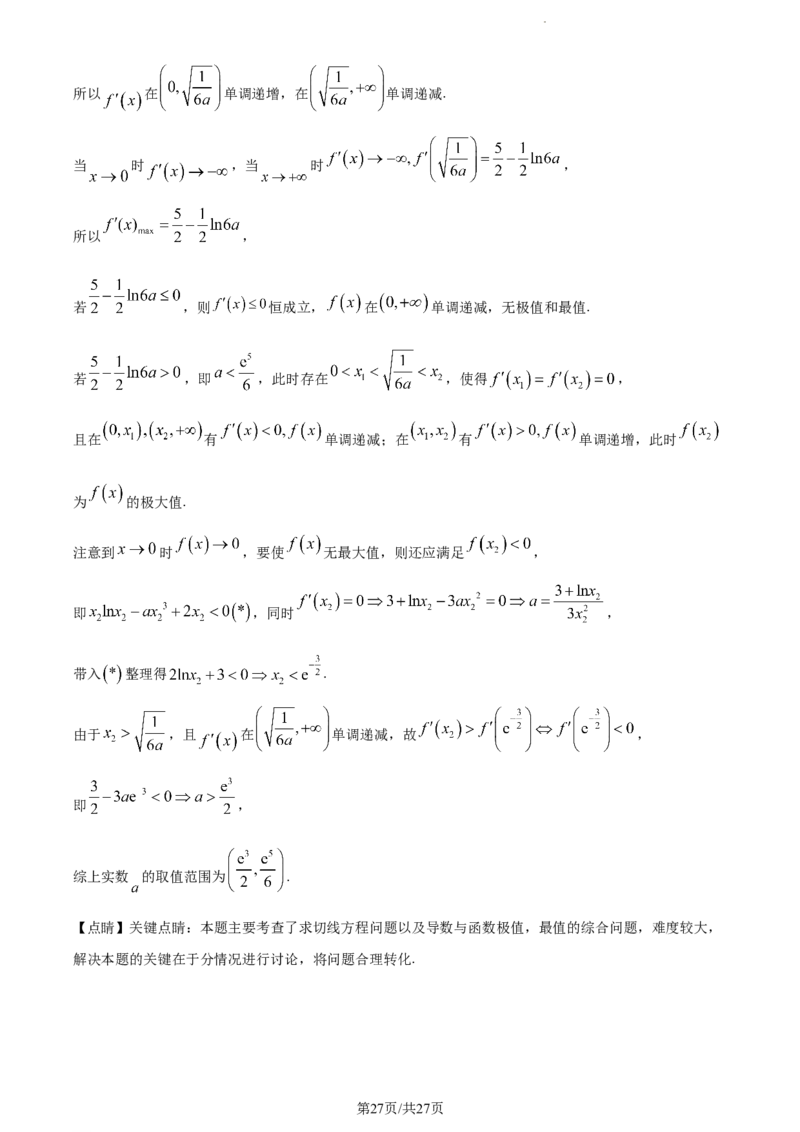文档内容
2023 年重庆一中高 2024 届高三上期开学考试
数学测试试题卷
注意事项:
1.答题前,考生务必用黑色碳索笔将自己的姓名、准考证号、考场号、座位号在答题卡上填
写清楚.
2.作答时,务必将答案写在答题卡上,写在本卷或者草稿纸上无效.
3.考试结束后,请将本试卷和答题卡一并交回.满分150分,考试用时120分钟.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 集合 的真子集个数为( )
A. 7 B. 8 C. 15 D. 16
【答案】A
【解析】
【分析】由对数函数定义域可求得 ,根据元素个数即可求出真子集个数.
【详解】根据题意可知 ,解得 ;
即 ,可知集合 中含有3个元素,
所以其真子集个数为 个.
故选:A
2. 已知符号函数 则“ ”是“ ”的( )
A. 充要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】根据充要条件的定义判断可得答案.
【详解】若 ,则 异号,所以 ,
第1页/共27页
学科网(北京)股份有限公司故“ ”是“ ”的充要条件.
故选:A.
3. 已知函数 ,则 ( )
A. B. 0 C. 4 D. 6
【答案】A
【解析】
【分析】根据分段函数的解析式,可得答案.
【详解】由题意可知:
,
, .
故选:A.
4. 一组数据按从小到大的顺序排列如下: ,经计算,该组数据中位数是16,若
分位数是20,则 ( )
A. 33 B. 34 C. 35 D. 36
【答案】D
【解析】
【分析】利用中位数和百分位数的定义得到 , ,求出答案.
【详解】一共有9个数,故从小到大的第5个数为中位数,即 ,
,故选取第7个数为 分位数,故 ,
所以 .
故选:D
第2页/共27页
学科网(北京)股份有限公司5. 已知 是定义在 上的奇函数. ,且当 时, ,
则 ( )
A. 0 B. C. 1 D. 2
【答案】C
【解析】
【分析】根据对称性与奇偶性得到 的周期为 ,再求出 及 ,最后根据周期性计算
可得.
【详解】由 满足 ,可得 的对称中心为 ,则 ,
又函数 为奇函数,所以 ,
所以 ,即 ,所以函数 的周期为 ,
又 ,令 ,则 ,
是定义在 上的奇函数,则 ,
又当 时, ,
则 ,
,
所以 .
故选:C.
6. 已知 为 中不同数字的种类,如
,记“ ”为事件 ,则事件 发生的概率 (
)
A. B. C. D.
第3页/共27页
学科网(北京)股份有限公司【答案】B
【解析】
【分析】由题意给的定义求出 的排列有256种,当 时,即排列中有2个不同
的数字,结合排列组合的应用计算即可求解.
【详解】由题意知, 的排列共有 种.
当 时,即排列中有2个不同的数字:
若有3个数字相同,有 种情况;
若有2个数字相同,有 种情况,
此时共有 种情况,所以事件A的概率为:
.
故选:B.
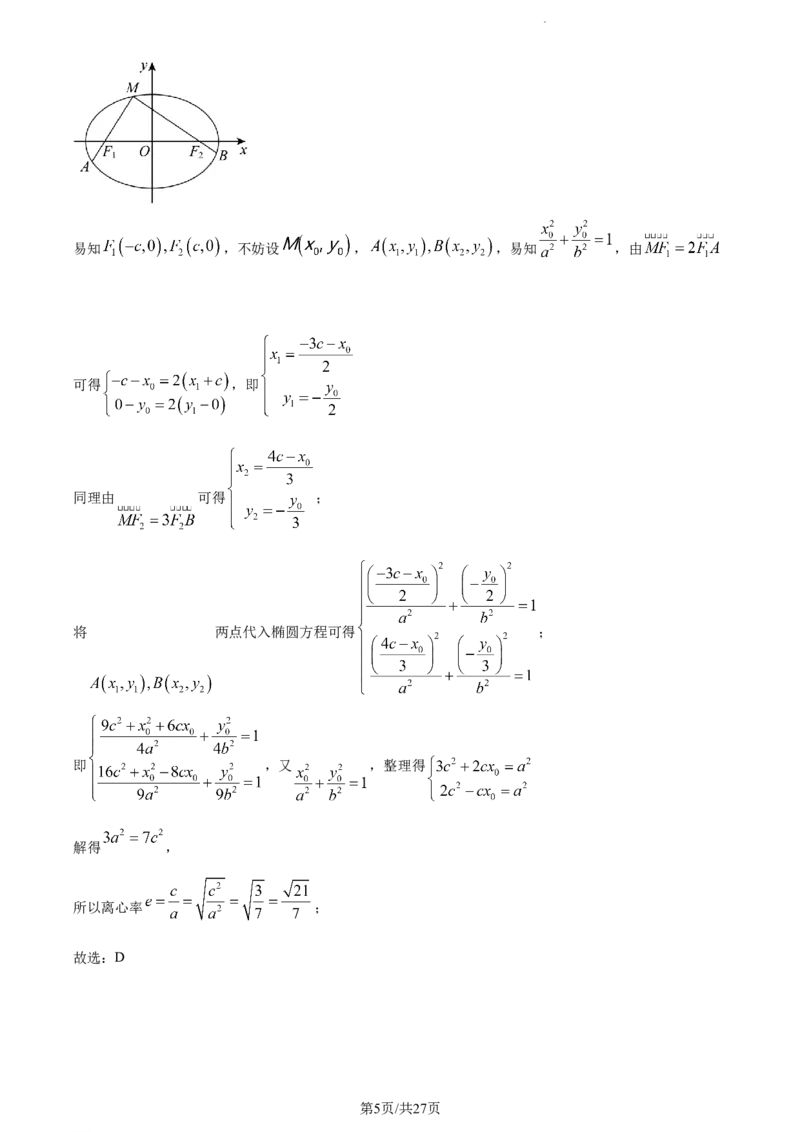
7. 设 分别为椭圆 的左右焦点,M为椭圆上一点,直线 分别交椭圆
于点A,B,若 ,则椭圆离心率为( )
A. B. C. D.
【答案】D
【解析】
【分析】设出 ,根据向量的定比分点,将 两点的坐标表示成含 的式子,再代入椭圆
方程联立即可解得 ,即可求得离心率.
【详解】如下图所示:
第4页/共27页
学科网(北京)股份有限公司易知 ,不妨设 , ,易知 ,由
可得 ,即
同理由 可得 ;
将 两点代入椭圆方程可得 ;
即 ,又 ,整理得
解得 ,
所以离心率 ;
故选:D
第5页/共27页
学科网(北京)股份有限公司8. 已知实数 满足: ,则( )
A. B. C. D.
【答案】A
【解析】
【分析】构造 , ,求导,得到函数单调性,得到 ,从而
;构造 , ,求导后得到函数单调性,得到
, 设 , 则 , 从 而 得 到 , 取 得 到
,从而求出答案.
【详解】令 , ,
故 在 上恒成立,
故 在 上单调递增,
故 ,即 , ,
所以 , ,
令 , ,
第6页/共27页
学科网(北京)股份有限公司则 在 上恒成立,
故 ,所以 ,
设 ,则 ,
故 ,所以 ,
即 ,由于 , ,
故 ,取 得: .
所以 .
故选:A
二、选择题:本题共4题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知实数 满足 ,则( )
A. B.
C. D.
【答案】CD
【解析】
【分析】根据指数函数单调性可得 ,可判断A错误;构造函数
可知,当 时 ,即B错误;利用函数 在 上为单调递增可知C正确;
利用作差法可判断D正确.
第7页/共27页
学科网(北京)股份有限公司【详解】对于A,根据指数函数 在 上单调递增,又 ,
所以 ,即 ,可得 ,所以A错误;
对于B,构造函数 ,易知 ,
当 时, ,所以 在 上单调递增,
当 时, ,所以 在 上单调递减;
所以可得 时, ,此时 ,即 ,所以B错误;
对于C,令 ,则 ,
所以函数 在 上为单调递增,即 ,又 ,
可得 ,即选项C正确;
对于D,由 可得 ,即 ,所以D正
确;
故选:CD
10. 某儿童乐园有甲,乙两个游乐场,小王同学第一天去甲、乙两家游乐场游玩的概率分别为 0.3和0.7,
如果他第一天去甲游乐场,那么第二天去甲游乐场的概率为 0.7;如果第一天去乙游乐场,那么第二天去
甲游乐场的概率为0.6,则王同学( )
A. 第二天去甲游乐场的概率为0.63
的
B. 第二天去乙游乐场 概率为0.42
C. 第二天去了甲游乐场,则第一天去乙游乐场的概率为
第8页/共27页
学科网(北京)股份有限公司D. 第二天去了乙游乐场,则第一天去甲游乐场的概率为
【答案】AC
【解析】
【分析】利用条件概率公式、全概率公式以及对立事件的概率计算公式一一代入计算即可.
【详解】设 :第一天去甲游乐场, :第二天去甲游乐场, :第一天去乙游乐场, :第二天去乙
游乐场,
依题意可得 , , , ,
对A, ,A正确;
对B, ,B错误;
对C, ,C正确;
对D, ,D错误,
故选:AC.
11. 设 ,则下列结论正确的是( )
A. 的最大值为 B. 的最大值为
C. 的最小值为 D. 的最小值为
【答案】BCD
【解析】
【分析】运用消元法、平均值换元法,结合柯西不等式、基本不等式逐一判断即可
【详解】A:因为 ,所以 ,即 ,
,显然该函数在 时,单调递增,
因此该函数此时没有最大值,因此本选项不正确;
第9页/共27页
学科网(北京)股份有限公司B: ,
因为 ,
所以 ,当且仅当 时取等号,
所以 ,即 的最大值为 ,因此本选项正确;
C:因为 ,
所以不妨设 ,设 ,
,
函数 在 时,单调递增,故 ,
因此本选项正确;
D:因为 ,
2
所以
a5+b5
=
a4
+
b4
=
(a4
+
b4
) (a+b)≥
[
(
a2
⋅√b ) + (
b2
⋅√a )
]
=(a2+b2) 2 ,
ab b a b a √b √a
而(a2+b2) 2 ≥ [(a+b) 2] 2 = 1 ,当且仅当 时,取等号,
2 4
即 的最小值为 ,因此本选项正确,
故选:BCD
【点睛】关键点睛:本题关键在于运用柯西不等式和平均值换元法.
12. 已知函数 ( )
第10页/共27页
学科网(北京)股份有限公司A. 若 ,则 是增函数
B. 若 ,则
C. 若 ,则 可能有两个零点
D. 若 ,则
【答案】ABD
【解析】
【分析】利用导数即可判断 A;根据不等式的性质及指数函数的单调性即可判断 B;易得函数
在 单调递减,即可判断C;由 ,得 ,则
有两个不同的正根 ,构造函数 ,利用导数求出 的具体关
系,再构造函数 ,利用导数判断其单调性,进而可判断D.
【详解】对于A选项,若 , ,则 ,
令 ,则 ,
当 时, ,当 时, ,
所以 在 上单调递减,在 上单调递增,
所以 ,
所以 ,故 ,所以 在 上是增函数,故A对;
第11页/共27页
学科网(北京)股份有限公司对于B选项, ,则 ,
故 ,从而 ,故B对;
对于C选项,若 ,则 ,
因为函数 在 都是减函数,
所以函数 在 单调递减,
故函数 最多只有一个零点,故C错;
对于D选项, ,则 ,
又 ,
则 有两个不同的正根 ,
由 ,得 ,
令 ,则 ,
当 时, ,当 时, ,
所以 在 上单调递减,在 上单调递增,
所以 ,
又当 时, ,当 时, ,
作出函数 的大致图像,如图所示,
第12页/共27页
学科网(北京)股份有限公司由图可得,要使 有两个不同的正根 ,则 ,
又 ,则 ,
而 ,同理 ,
构造函数 ,则 恒成立,
故 在 单调递减,
,则 ,即 ,
令 ,则 ,
当 时, ,当 时, ,
所以函数 在 上单调递减,在 上单调递增,
所以 ,即 ,当且仅当 时取等号,
又 ,则 ,
第13页/共27页
学科网(北京)股份有限公司故 ,
故 ,故D对.
【点睛】方法点睛:利用导数证明不等式问题,方法如下:
(1)直接构造函数法:证明不等式 (或 )转化为证明 (或
),进而构造辅助函数 ;
(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用常见放缩结论;
(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.
三、填空题:本题共4小题,每小题5分,共20分.
13. 若随机变量 ,且 ,则 ________.
【答案】0.2##
【解析】
【分析】利用正态分布的对称性即可求出结果.
【详解】由随机变量 , ,
利用正态分布的对称性计算可知 ,
故答案为:0.2
14. 二项式 展开式的常数项是__________.
【答案】
【解析】
【分析】先求出通项公式,再令 的幂指数等于 ,求得 的值,即可求得展开式中的常数项的值.
【详解】由于 的展开式的通项公式为:
第14页/共27页
学科网(北京)股份有限公司,
令 ,解得 ,
则其展开式的常数项为 .
故答案为:
15. 已知函数 满足 ,若 在其定义域内单调递减,则正实数m
的取值范围为_________.
【答案】
【解析】
【分析】先求得 的解析式,然后根据 的单调性,由 分离参数 ,结合基本不等式求
得 的取值范围.
【详解】依题意, ,
令 ,则 ,
所以 ,
所以 .
所以 , 的定义域是 ,
依题意 在 上单调递减,
若 ,则 在 上单调递增,不符合题意.
当 时,由于 和 在 上单调递增,
第15页/共27页
学科网(北京)股份有限公司所以 在 上单调递增,不符合题意.
当 时, ,在 上恒成立,
即 在 上恒成立,
即 在 上恒成立,
由于 ,当且仅当 时等号成立,
所以 ,所以 .
故答案为:
16. 已知函数 定义域为 , ,且满足 ,其中 为 的导函数,若
不等式 恒成立,则正实数 的最小值
为_________.
【答案】
【解析】
【分析】构造函数 ,讨论单调性可得 ,进而可得
,再构造函数 讨论单调性可得 ,从
第16页/共27页
学科网(北京)股份有限公司而构造函数 求最大值即可求解.
【详解】由 可知 单调递增.
不等式变形为 ,
构造 , 在定义域 恒成立,
所以 在 上单调递增,
故 ,即 ,
进一步变形得: ,
构造
设 ,
当 时, ,当 时, ,
所以 在 单调递减,在 单调递增,
.
故 单调递增
(*)等价于 ,即 恒成立,
构造函数 , ,
令 解得 ,令 解得 ,
所以 的最大值为 ,所以 ,即正实数 的最小值为 .
第17页/共27页
学科网(北京)股份有限公司故答案为: .
【点睛】关键点点睛:本题解题关键是构造两个函数 , ,以及二次求导
研究函数的单调性及最值,是一道有难度的题.
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
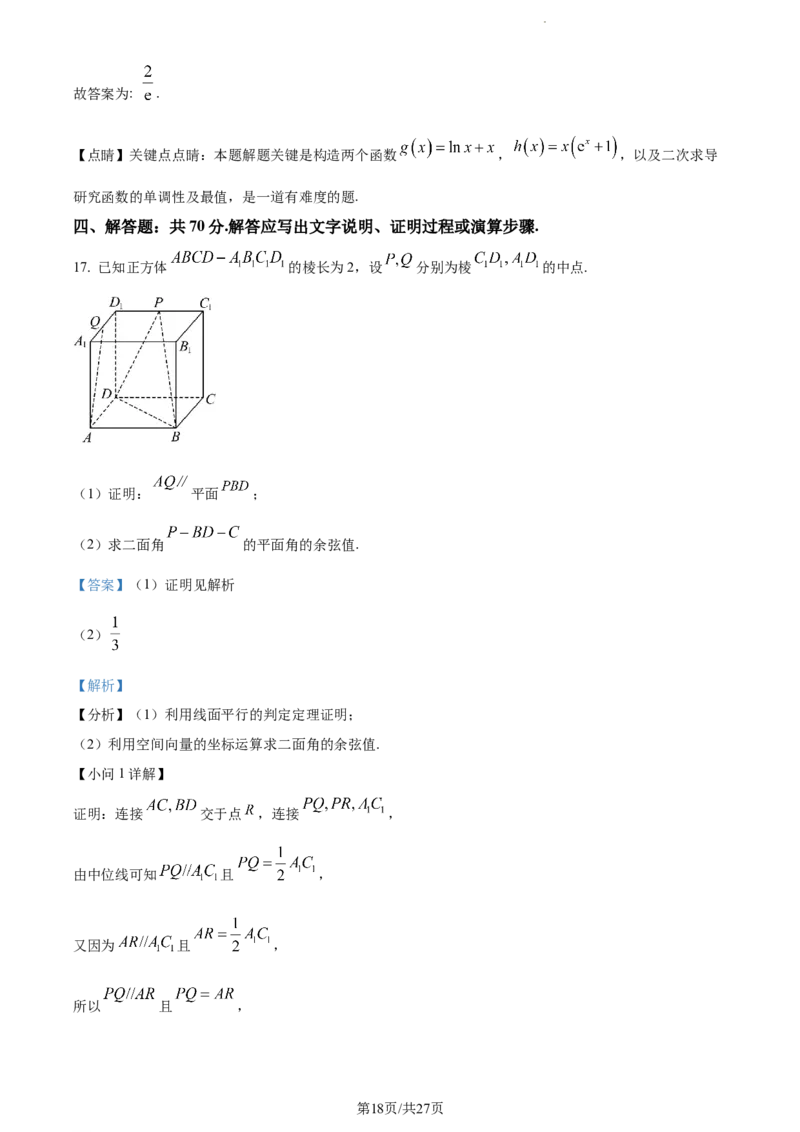
17. 已知正方体 的棱长为2,设 分别为棱 的中点.
(1)证明: 平面 ;
(2)求二面角 的平面角的余弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)利用线面平行的判定定理证明;
(2)利用空间向量的坐标运算求二面角的余弦值.
【小问1详解】
证明:连接 交于点 ,连接 ,
由中位线可知 且 ,
又因为 且 ,
所以 且 ,
第18页/共27页
学科网(北京)股份有限公司为
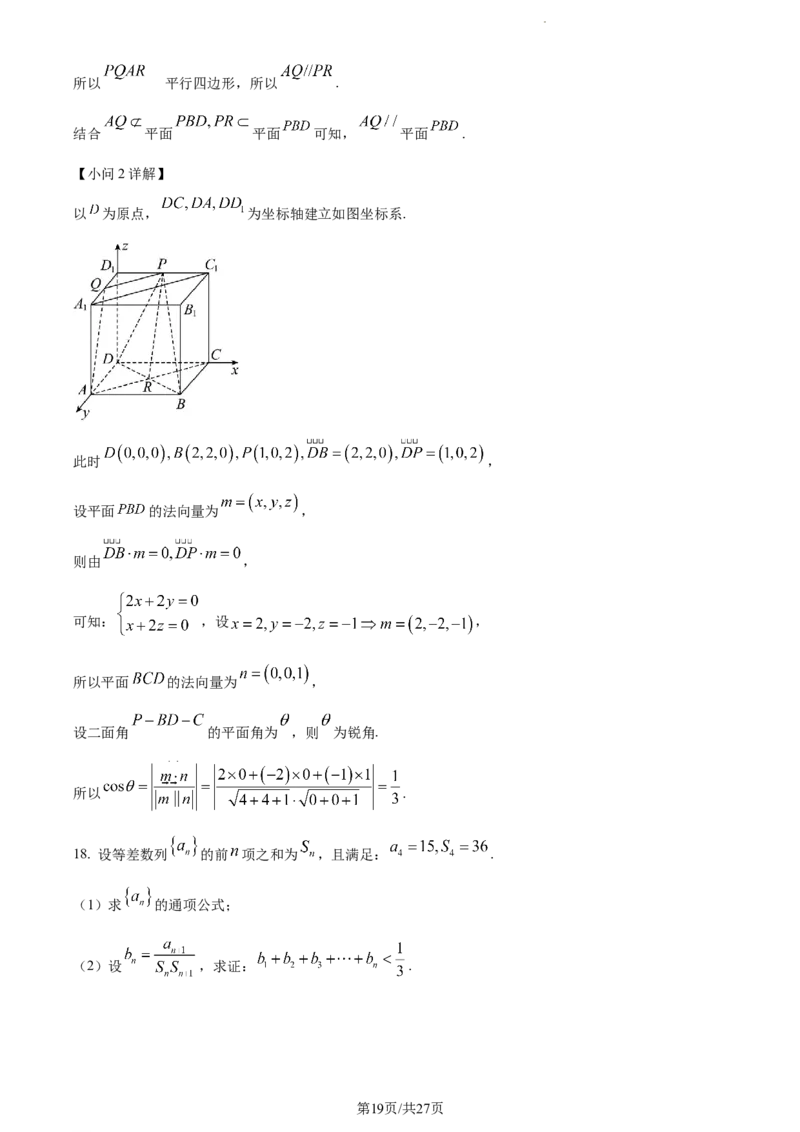
所以 平行四边形,所以 .
结合 平面 平面 可知, 平面 .
【小问2详解】
以 为原点, 为坐标轴建立如图坐标系.
此时 ,
设平面 的法向量为 ,
则由 ,
可知: ,设 ,
所以平面 的法向量为 ,
设二面角 的平面角为 ,则 为锐角.
所以 .
18. 设等差数列 的前 项之和为 ,且满足: .
(1)求 的通项公式;
(2)设 ,求证: .
第19页/共27页
学科网(北京)股份有限公司【答案】(1)
(2)证明见解析
【解析】
【分析】(1)根据等差数列的的基本量计算求解;
(2)利用裂项相消法求和.
【小问1详解】
设 的公差为 ,则由已知 ,
解得 ,所以 .
【小问2详解】
由于 ,
所以 .
19. 已知 、 分别为定义域为 的偶函数和奇函数,且 .
(1)求 的单调区间;
(2)对任意实数 均有 成立,求实数 的取值范围.
【答案】(1) 的增区间为 ,减区间为
(2)
【解析】
【分析】(1)对于 将 换成 结合奇偶性求出 、 的解析式,在利用导数
求出函数的单调区间;
(2)设 ,则问题转化为 在 时恒成立,参变分离可得 ,再
第20页/共27页
学科网(北京)股份有限公司利用基本不等式求出 的最小值,即可求出 的取值范围.
【小问1详解】
因为 ①, 、 分别为定义域为 的偶函数和奇函数,
所以 , ,
所以 ,即 ②,
①②解得 , ,
所以 , ,
所以 ( )在定义域 上单调递增,又 ,
所以当 时 ,即 的单调递增区间为 ,
当 时 ,即 的单调递减区间为 .
【小问2详解】
设 ,因为 ,当且仅当 时取等号,所以 ,
不等式 恒成立,转化为 在 时恒成立,
分离参数得 在 时恒成立,由均值不等式 ,当且仅当 时取等
号,
故 的最小值为 ,所以 ,
故实数 的取值范围为 .
20. 甲、乙两人轮流投篮,约定甲先投,先投中者获胜,直到有人获胜或每人都已投球 次时投篮结束,
第21页/共27页
学科网(北京)股份有限公司其中 为给定正整数.设甲每次投中的概率为 ,乙每次投中的概率为 ,且各次投篮互不影响.
(1)当 时,求甲获胜的概率;
(2)设投篮结束时甲恰好投篮 次,求 的数学期望 .(答案用含 的最简式子表示).
【答案】(1)
(2)
【解析】
【分析】(1)分甲投球1次获胜、甲投球2次获胜和甲投球3次获胜三种情况,计算相应的概率相加即可;
(2)根据投篮次数的取值,计算相应的概率,由公式求数学期望,借助数列求和的错位相减法化简.
【小问1详解】
甲投球1次获胜的概率 ,甲投球2次获胜的概率 ,
甲投球3次获胜的概率 ,
所以甲获胜的概率 .
【小问2详解】
记“甲第 次投中”为事件 ,“乙第 次投中”为事件 ,其中 ,
当 时,投篮结束时甲恰好投篮 次的概率为: ,
投篮结束时甲恰好投篮 次的概率为:
,
第22页/共27页
学科网(北京)股份有限公司所以 ,
设 ,则 ,
则 ,错位相减得:
,
所以 .
21. 已知椭圆 的左顶点为 ,上顶点为 ,右焦点为 ,设 为坐标原点,
线段 的中点为 ,且满足 .
(1)求椭圆 的标准方程;
(2)设点 ,圆 过 且交直线 于 两点,直线 分别交 于另一点
(异于点 ).证明:直线 过定点,并求出该定点的坐标.
【答案】(1)
(2)证明见解析,
【解析】
【分析】(1)根据题意求出 即可得解;
(2)设 ,先求出圆 的方程,令 ,利用韦达定理求出
,设直线 的方程为 ,联立方程,利用韦达定理求出 ,再根据 三点
第23页/共27页
学科网(北京)股份有限公司共线得 ,求出 ,同理求出 ,整理可得出答案.
【小问1详解】
由题意 ,
由 可知: ,
整理得 ,所以 ,
所以椭圆 的方程为 ;
【小问2详解】
设 ,
依题意,圆 的方程为 ,
令 ,则 , ,
由韦达定理可得 ,
由已知直线 不与 轴垂直,设直线 的方程为 ,
与椭圆联立得: ,
由韦达定理可得 ,
由 三点共线得 ,
所以 ,
同理 ,
第24页/共27页
学科网(北京)股份有限公司所以 ,
去分母整理得: ,
将韦达定理带入得: ,
整理得 或 ,
当 时,直线 过点 ,不合题意,所以 ,
所以直线 的方程为 ,恒过定点 .
【点睛】方法点睛:求解直线过定点问题常用方法如下:
(1)“特殊探路,一般证明”:即先通过特殊情况确定定点,再转化为有方向、有目的的一般性证明;
(2)“一般推理,特殊求解”:即设出定点坐标,根据题设条件选择参数,建立一个直线系或曲线的方
程,再根据参数的任意性得到一个关于定点坐标的方程组,以这个方程组的解为坐标的点即为所求点;
(3)求证直线过定点 ,常利用直线的点斜式方程 或截距式 来证明.
22. 已知函数 .
(1)设 ,经过点 作函数 图像的切线,求切线的方程;
(2)若函数 有极大值,无最大值,求实数 的取值范围.
第25页/共27页
学科网(北京)股份有限公司【答案】(1)
(2)
【解析】
【分析】(1)根据题意,求导得 ,再由导数的几何意义,即可得到结果;
(2)根据题意,求导得 ,令 ,然后分 与 两种情况,分别讨论,即可得到
结果.
【小问1详解】
时 ,
设切点为 ,则切线斜率为 ,
切线方程: ,
将点 带入得: ,
此时斜率 ,所以切线方程为 .
【小问2详解】
函数 的定义域为 ,令 ,则
(1)当 时 在 单调递增,
注意到 时, ,注意到 时, ,
故存在 ,使得 ,在 时 单调递减,在 时,
单调递增,函数 有极小值,无极大值,不符合题意.
(2)当 时,令 ,令 ,
第26页/共27页
学科网(北京)股份有限公司所以 在 单调递增,在 单调递减.
当 时 ,当 时 ,
所以 ,
若 ,则 恒成立, 在 单调递减,无极值和最值.
若 ,即 ,此时存在 ,使得 ,
且在 有 单调递减;在 有 单调递增,此时
为 的极大值.
注意到 时 ,要使 无最大值,则还应满足 ,
即 ,同时 ,
带入 整理得 .
由于 ,且 在 单调递减,故 ,
即 ,
综上实数 的取值范围为 .
【点睛】关键点睛:本题主要考查了求切线方程问题以及导数与函数极值,最值的综合问题,难度较大,
解决本题的关键在于分情况进行讨论,将问题合理转化.
第27页/共27页
学科网(北京)股份有限公司