文档内容
2022-2023学年小学六年级思维拓展举一反三精编讲义
专题02 简便运算
知识精讲
根据算式的结构和数的特征,灵活运用运算法则、定律、性质和某些公式,
可以把一些较复杂的四则混合运算化繁为简,化难为易。
在进行分数运算时,除了牢记运算定律、性质外,还要仔细审题,仔细观察
运算符号和数字特点,合理地把参加运算的数拆开或者合并进行重新组合,
使其变成符合运算定律的模式,以便于口算,从而简化运算。
典例分析
【典例分析01】计算:2×23.4+11.1×57.6+6.54×28
原式=2.8×23.4+2.8×65.4+11.1×8×7.2
=2.8×(23.4+65.4)+88.8× 7.2
=2.8×88.8+88.8×7.2
=88.8×(2.8+7.2)
=88.8×10
=888
【典例分析02】计算333387×79+790×66661
原式=333387.5×79+790×66661.25
=(33338.75+66661.25)×790
=100000×790
=79000000
【典例分析03】计算:36×1.09+1.2×67.3
原式=1.2×30×1.09+1.2×67.3
=1.2×(32.7+67.3)
=1.2×100=120
【典例分析01】计算:3×25+37.9×6
原式=3×25+(25.4+12.5)×6.4
=3×25+25.4×6.4+12.5×6.4
=(3.6+6.4)×25.4+12.5×8×0.8
=254+80
=334
【典例分析01】计算81.5×15.8+81.5×51.8+67.6×18.5
原式=81.5×(15.8+51.8)+67.6×18.5
=81.5×67.6+67.6×18.5
=(81.5+18.5)×67.6
=100×67.6
=6760
真题演练
一.选择题(共5小题,满分10分,每小题2分)
1.(2分)(2021秋•邢台期末)如果甲×0.25=乙÷0.25(甲、乙都不为0),那么甲
( )乙。
A.> B.= C.< D.无法确定
【思路点拨】假设甲×0.25=乙÷0.25=1(甲数、乙数都不为0),则甲数=4、乙数
=0.25,由此即可得出甲数、乙数的大小。
【规范解答】解:假设甲×0.25=乙÷0.25=1(甲数、乙数都不为0)
则甲数=4、乙数=0.25
因为4>0.25
则甲数>乙数
故选:A。
【考点评析】本题运用假设法,分别求出甲数、乙数的值,再比较大小,做出选择。
2.(2分)(2022秋•诸城市期末) ÷ =( )A.25 B.125 C.1250 D.250
【思路点拨】小数除法计算方法:先移动除数的小数点,使它变成整数;除数的小数点
向右移动几位,被除数的小数点也向右移动几位,位数不够时,在被除数的末尾用0补
足;最后按照除数是整数的除法进行计算。
【规范解答】解:除数小数部分有11位,则将被除数和除数的小数点向右移动11位,
转化成6250÷25=250
故选:D。
【考点评析】本题主要考查了学生对小数除法的计算方法的掌握。
3.(2分)(2022秋•济南期末)与1+3+5+7+9+5+3+1表示结果相同的算式是( )
A.(5+3)2 B.42 C.52 D.52+32
【思路点拨】运用加法交换律a+b+c=a+c+b和结合律(a+b)+c=(a+c)+b计算出结
果,然后与三个选项进行比较。
【规范解答】解:1+3+5+7+9+5+3+1
=(1+9)+(3+7)+(5+5)+3+1
=10+10+10+4
=34
52+32
=25+9
=34
根据计算过程可知,D选项正确。
故选:D。
【考点评析】本题主要考查了加法的巧算,也可总结算式的规律,从1开始,连续奇数
的和等于奇数个数的平方来求解。
4.(2分)(2022秋•峰峰矿区期末) + + + + =( )
A.1 B. C. D.2
【思路点拨】根据分数的拆项公式 = ,即可求出。
【规范解答】解:
=1=1
=
故选:B。
【考点评析】考查分数的拆项公式 = ,要根据实际灵活运用。
5.(2分)(2022秋•唐河县期末) + + + + +……+ =( )
A. B.1 C. D.无法计算
【思路点拨】 =1﹣ , = ﹣ , = ﹣ ……,从第二个加数开始,后一个加
数可以变成前一个加数减本身的形式。
【规范解答】解: + + + + +……+
=1﹣ + ﹣ + ﹣ + ﹣ + ﹣ +……﹣
=1﹣
=
故选:C。
【考点评析】仔细观察,合理变形是解决本题的关键。
二.填空题(共8小题,满分16分,每小题2分)
6.(2分)(2021秋•长垣市期末)已知A= .B= ,则A÷B=
3 2 。
【思路点拨】根据商不变的性质进行解答即可。
【规范解答】解:A÷B
= ÷
=96÷3
=32
故答案为:32。【考点评析】解答本题的关键是分析两个小数都是几位小数,再根据小数的除法计算方
法,移动除数和被除数的小数点的位置即可解答。
7.(2分)(2021秋•殷都区期末)9.87×5.6的积是 三 位小数。【思路点拨】根据小数乘法的计算方法知:积的小数位数等于因数中小数位数的和,据
此解答。
【规范解答】解:9.87×5.6中的因数中一共有三位小数,所以积中也是三位小数。
故答案为:三。
【考点评析】考查了小数乘法中因数与积的小数位数之间的关系。
8.(2分)(2021秋•殷都区期末)根据5.6×2.8=15.68,直接写出下面算式的得数。
0.56×0.28= 0.156 8 560×0.28= 156. 8
【思路点拨】根据积的变化规律,5.6缩小到原数的 ,2.8缩小到原数的 ,那么
积就缩小到原数的 ,即0.56×0.28=0.1568;5.6扩大100倍,2.8缩小到原数的
,那么积就扩大10倍,即560×0.28=156.8。
【规范解答】解:根据5.6×2.8=15.68,直接写出下面算式的得数。
0.56×0.28=0.1568 560×0.28=156.8
故答案为:0.1568;156.8。
【考点评析】此题主要考查了积的变化规律的灵活应用。
9.(2 分)(2022 秋•稷山县期末)1+3+5+7+9+11+13+15+17+19+21= 121 ,
1+3+5+7+9+7+5+3+1= 4 1 。
【思路点拨】观察算式,每相邻两个加数都相差2,发现:
2个加数的和:1+3=4=22;
3个加数的和:1+3+5=9=32;
4个加数的和:1+3+5+7=16=42
……
规律:n个加数的和=n2;
据此规律解答。
观察算式可得,算式为连续的奇数相加求和,对于像 1,3,5这样的连续奇数求和,首
尾两数之和等于中间的数的2倍,以此类推。由此解答即可。
【规范解答】解:1+3+5+7+9+11+13+15+17+19+21
=112
=1211+3+5+7+9+7+5+3+1
=(1+9)+(3+7)+5+(5+3)+(7+1)
=(2×5+2×5+1×5)+(2×4+2×4)
=5×5+4×4
=52+42
=25+16
=41
故答案为:121;41。
【考点评析】本题是找规律的题型,从已知的数据中找到规律,并按规律解题。
10.(2分)(2021秋•威信县期末)1﹣( +……)= 0
【思路点拨】根据分数拆项方法,把 + + + + + +.....,转化为:(1
)+( )+( )+( )+( )+( )+......,然后去掉
括号,加减抵消进行简算。
【规范解答】解: + + + + + +......
=(1 )+( )+( )+( )+( )+( )+......
= ﹣ +......
=1﹣ +.....
=1
所以1﹣( +……)=0
故答案为:0。
【考点评析】此题考查的目的是理解掌握分数的拆项方法及应用,以及数与形结合的应
用。
11.(2 分)(2022•重庆)0. 2 +0. 3 +0. 4 +0. 5 +0. 6 +0. 7 =
。
【思路点拨】题中的循环小数都是纯循环小数,把纯循环小数化成分数后计算,将纯循环小数改写为分数,分子是一个循环节的数字组成的数,分母各位数字都是 9,9的个
数与循环节中的数字的个数相同,最后能约分的再约分。【规范解答】解:0. 2 +0. 3 +0. 4 +0. 5 +0. 6 +0. 7
= + + + + +
=
=2
=
故答案为: 。
【考点评析】此题考查了小数的巧算,以及纯循环小数化分数的方法。
12 . ( 2 分 ) ( 2021 秋 • 安 顺 期 末 ) 计 算 : 1000﹣
= 55 0 。
【思路点拨】根据减法性质及加法结合律求解即可。
【规范解答】解:1000﹣( + + + + + + + + + + + + +
+ + + + )
=1000﹣[( + )+( + )+( + )+( + )+( + )+( +
)+( + )+( + )+( + )]
=1000﹣[50+50+50+50+50+50+50+50+50]
=1000﹣450
=550
故答案为:550。
【考点评析】本题主要考查了分数的巧算,解题的关键是灵活运用减法的性质及加法结
合律计算。
13.(2分)(2022•双牌县) + + +……+ = 。【思路点拨】观察发现没每个分数都能拆成两个分数的差,但变为原来的3倍,如
= ×( ﹣ ),据此解答即可。【规范解答】解: + + +……+
= ×( ﹣ + ﹣ + ﹣ +……+ ﹣ )
= ×( ﹣ )
= ×
=
故答案为: 。
【考点评析】本题主要考查分数的巧算,发现分数的特点是解本题的关键。
三.判断题(共5小题,满分10分,每小题2分)
14.(2分)(2020•铜官区) 。 √ (判断对错)
【思路点拨】从第三项开始,把每个分数拆成两个分数相减的形式,通过加减相互抵消,
求得结果。
【规范解答】解:1﹣ ﹣ ﹣ ﹣ ﹣
=1﹣( )
=1﹣( + )
=1﹣(1﹣ )
=
故答案为:√。
【考点评析】完成此题,注意分数的拆分,通过加减相互抵消,解决问题。
15.(2 分)(2021 秋•竹溪县期末) 。 √
(判断对错)
【思路点拨】对 进行分析推理猜想, ,, ……,对比观察,每加一个加数,分子与分母越来越大,在这
个过程中,该分数越来越接近1,所以可得这样延续下去最后就等于1。
【规范解答】解:由分析可得 的结果为1,所以可得得
到的结果为0。
故答案为:√。
【考点评析】通过列举例子,进行合理的推理猜想,找到其中的规律即可得到答案。
16.(2分)(2021秋•恩平市期末)在1+3+5+7+9+…中,从数“1”到数“15”的和是
64。………………… √ (判断对错)
【思路点拨】1+3+5+7+9+…是等差数列的求和,共有8个数,运用高斯求和定理即可求
得。
【规范解答】解:1+3+5+7+9+…+15
=(1+15)×8÷2
=16×8÷2
=64
故答案为:√。
【考点评析】仔细观察,找到数字的特点运用合适的定律或定理来解答。
17.(2分)(2012•华坪县模拟) 约分后等于 . √ .(判断对
错)
【思路点拨】根据乘法的分配律把分数的分子和分母变形,然后约分化成最简分数,看
得数是否等于 即可判断.
【规范解答】解:
=
=
=
所以,所以原题说法正确.
故答案为:√.
【考点评析】本题关键是根据乘法的分配律把分数的分子和分母变形.
18.(2分)(2021秋•易县期末) +…=1。 × (判断对错)【思路点拨】设 + + + + +…+ =a,得出2×( + + + + +…+)=2a,两等式相减,得出a=1﹣ ,当n无限大时, 就会无限小,所以a无限接
近1,但不等于1,据此判断即可。
【规范解答】解:设 + + + + +…+ =a,则2×( + + + + +…+
)=2a,
2×( + + + + +…+ )﹣( + + + + +…+ )=2a﹣a
1+ + + + + +…+ ﹣( + + + + +…+ )=a
1+( + + + + +…+ )﹣( + + + + +…+ + )=a
1﹣ =a
当n无限大时, 就会无限小,所以a无限接近1,但不等于1,故原题 + + + +
+…=1错误。
故答案为:×。
【考点评析】本题主要考查了分数的巧算,解题的关键是观察式子找出规律。
四.计算题(共2小题,满分21分)
19.(12分)(2021秋•抚远市期末)能简算的要简算。
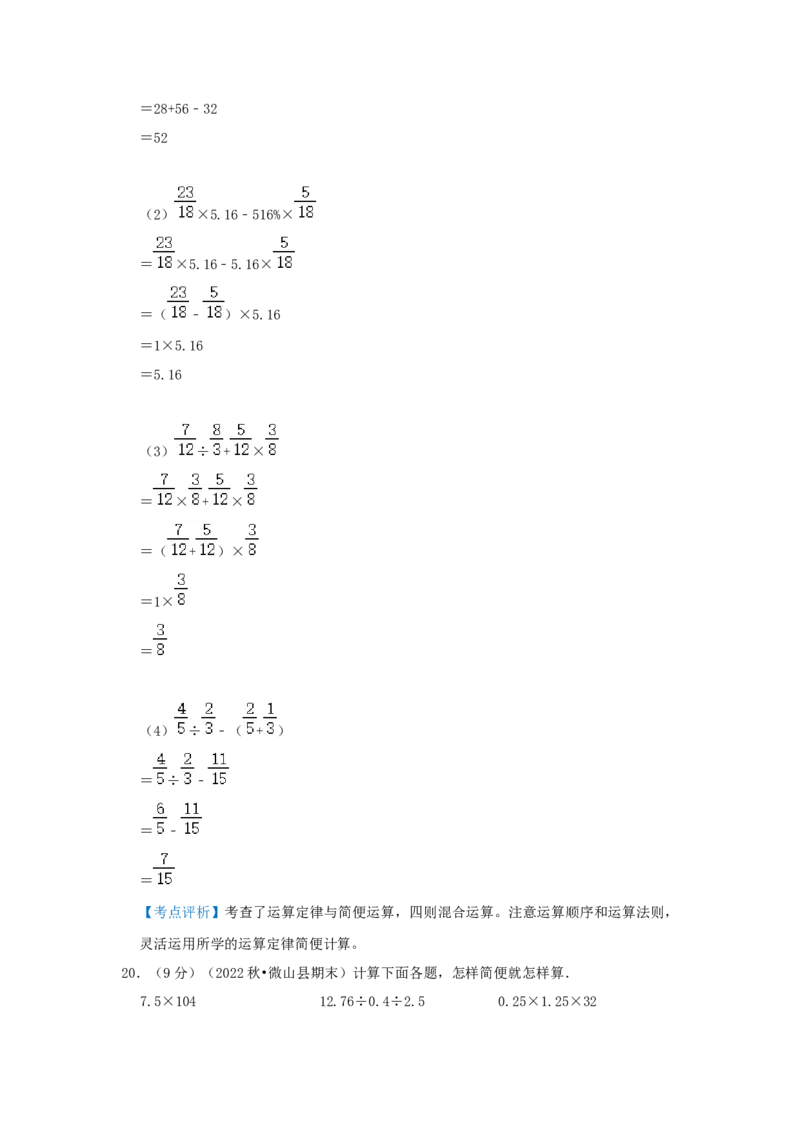
( + ﹣ ) ×5.16﹣ 516%× ÷ + × ÷ ﹣( + )
×96
【思路点拨】(1)、(2)、(3)根据乘法分配律进行简算;
(4)先算小括号里面的加法,再算括号外面的除法,最后算括号外面的减法。
【规范解答】解:(1)( + ﹣ )×96= ×96+ ×96﹣ ×96=28+56﹣32
=52
(2) ×5.16﹣516%×
= ×5.16﹣5.16×
=( ﹣ )×5.16
=1×5.16
=5.16
(3) ÷ + ×
= × + ×
=( + )×
=1×
=
(4) ÷ ﹣( + )
= ÷ ﹣
= ﹣
=
【考点评析】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,
灵活运用所学的运算定律简便计算。
20.(9分)(2022秋•微山县期末)计算下面各题,怎样简便就怎样算.
7.5×104 12.76÷0.4÷2.5 0.25×1.25×32【思路点拨】(1)根据乘法分配律简便计算;
(2)根据连除的性质即可求解;(3)变形为(0.25×4)×(1.25×8)简便计算.
【规范解答】解:(1)7.5×104
=7.5×(100+4)
=7.5×100+7.5×4
=750+30
=780
(2)12.76÷0.4÷2.5
=12.76÷(0.4×2.5)
=12.76÷1
=12.76
(3)0.25×1.25×32
=(0.25×4)×(1.25×8)
=1×10
=10
【考点评析】关于巧算的题目,数字都有一定的特点,所以要注意审题,从数字特点出
发,巧妙灵活地应用运算性质、定律得以简算.
五.解答题(共7小题,满分43分)
21.(4分)(2020秋•冷水滩区期末) + + + + =
。
【思路点拨】根据 , ……,把原式变形,然后再
进一步解答即可。
【规范解答】解: + + + +
=
=
=故答案为: 。
【考点评析】解答本题要找出规律,然后把原式根据规律化简,最后进行解答。
22.(9分)(2022•平凉模拟)简便计算
4.75﹣9.63+8.25﹣1.37
81.5×15.8+81.5×51.8+67.6×18.5
99999×26+33333×22.
【思路点拨】①可以先加8.25,然后再减去9.63,进而根据减法的性质进行简算即可;
②首先前面的两个乘法算式根据乘法分配律,提取81.5,和是67.6,然后和后面的乘
法算式根据乘法分配律,计算即可;
③把99999分解为33333×3,然后运用乘法结合律,可得:33333×3×26+33333×22,
然后运用乘法分配律进行简算即可.
【规范解答】解:①4.75﹣9.63+8.25﹣1.37
=4.75+8.25﹣9.63﹣1.37
=(4.75+8.25)﹣(9.63+1.37)
=13﹣11
=2
②81.5×15.8+81.5×51.8+67.6×18.5
=81.5×(15.8+51.8)+67.6×18.5
=81.5×67.6+67.6×18.5
=67.6×(81.5+18.5)
=67.6×100
=6760
③99999×26+33333×22
=33333×3×26+33333×22
=33333×78+33333×22
=33333×(78+22)
=3333300
【考点评析】考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,
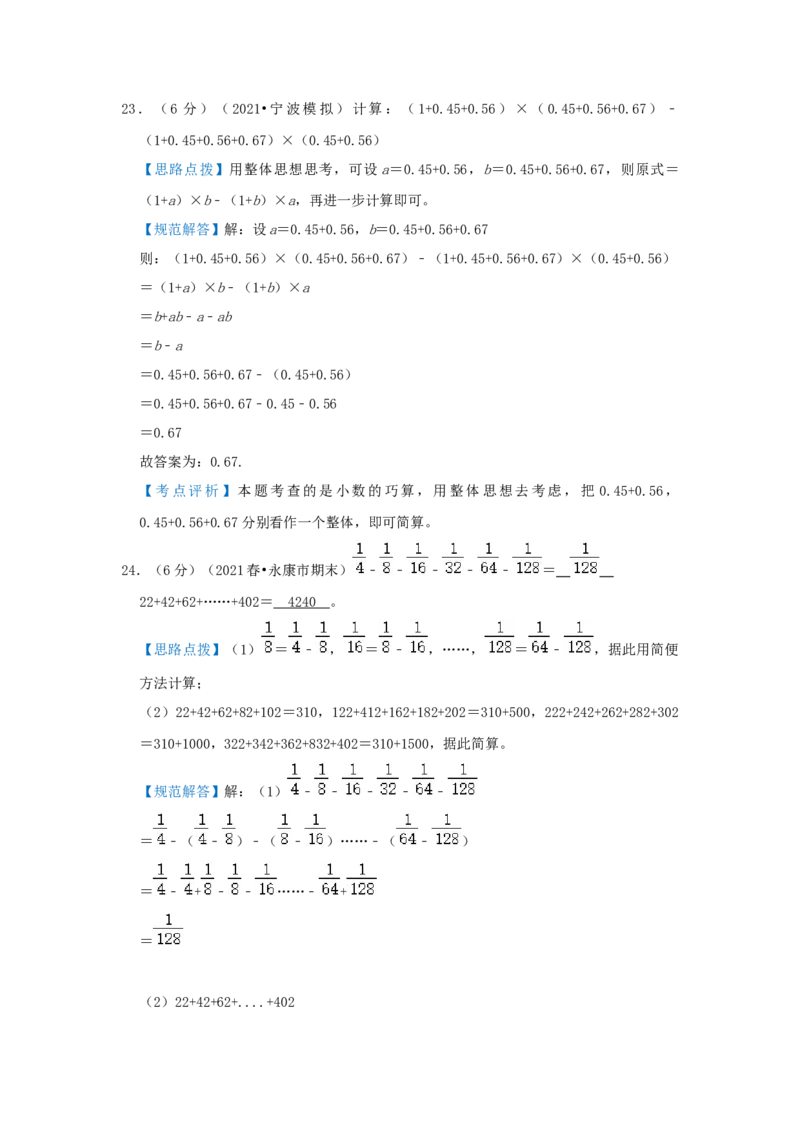
灵活运用所学的运算定律简便计算.23.(6 分)(2021•宁波模拟)计算:(1+0.45+0.56)×(0.45+0.56+0.67)﹣
(1+0.45+0.56+0.67)×(0.45+0.56)
【思路点拨】用整体思想思考,可设a=0.45+0.56,b=0.45+0.56+0.67,则原式=
(1+a)×b﹣(1+b)×a,再进一步计算即可。
【规范解答】解:设a=0.45+0.56,b=0.45+0.56+0.67
则:(1+0.45+0.56)×(0.45+0.56+0.67)﹣(1+0.45+0.56+0.67)×(0.45+0.56)
=(1+a)×b﹣(1+b)×a
=b+ab﹣a﹣ab
=b﹣a
=0.45+0.56+0.67﹣(0.45+0.56)
=0.45+0.56+0.67﹣0.45﹣0.56
=0.67
故答案为:0.67.
【考点评析】本题考查的是小数的巧算,用整体思想去考虑,把 0.45+0.56,
0.45+0.56+0.67分别看作一个整体,即可简算。
24.(6分)(2021春•永康市期末) ﹣ ﹣ ﹣ ﹣ ﹣ =
22+42+62+……+402= 424 0 。
【思路点拨】(1) = ﹣ , = ﹣ ,……, = ﹣ ,据此用简便
方法计算;
(2)22+42+62+82+102=310,122+412+162+182+202=310+500,222+242+262+282+302
=310+1000,322+342+362+832+402=310+1500,据此简算。
【规范解答】解:(1) ﹣ ﹣ ﹣ ﹣ ﹣
= ﹣( ﹣ )﹣( ﹣ )……﹣( ﹣ )
= ﹣ + ﹣ ﹣ ……﹣ +
=
(2)22+42+62+....+402= ( 22+42+62+82+102 ) +[ ( 22+42+62+82+102 ) +500]+
[(22+42+62+82+102)+500×2]+[(22+42+62+82+102)+500×3]
=310×4+500×6
=4240
故答案为: ;4240。
【考点评析】解答此类问题需灵活找规律简算。
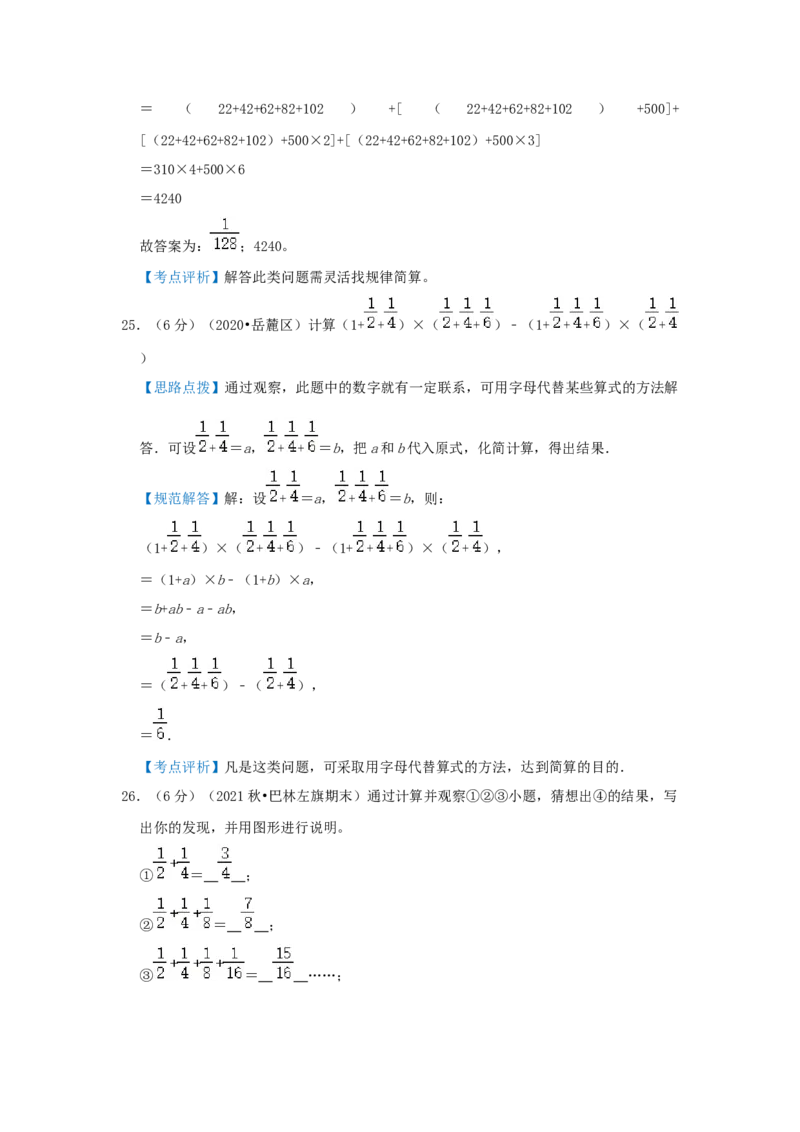
25.(6分)(2020•岳麓区)计算(1+ + )×( + + )﹣(1+ + + )×( +
)
【思路点拨】通过观察,此题中的数字就有一定联系,可用字母代替某些算式的方法解
答.可设 + =a, + + =b,把a和b代入原式,化简计算,得出结果.
【规范解答】解:设 + =a, + + =b,则:
(1+ + )×( + + )﹣(1+ + + )×( + ),
=(1+a)×b﹣(1+b)×a,
=b+ab﹣a﹣ab,
=b﹣a,
=( + + )﹣( + ),
= .
【考点评析】凡是这类问题,可采取用字母代替算式的方法,达到简算的目的.
26.(6分)(2021秋•巴林左旗期末)通过计算并观察①②③小题,猜想出④的结果,写
出你的发现,并用图形进行说明。
① = ;
② = ;
③ = ……;则:④ +……= 。
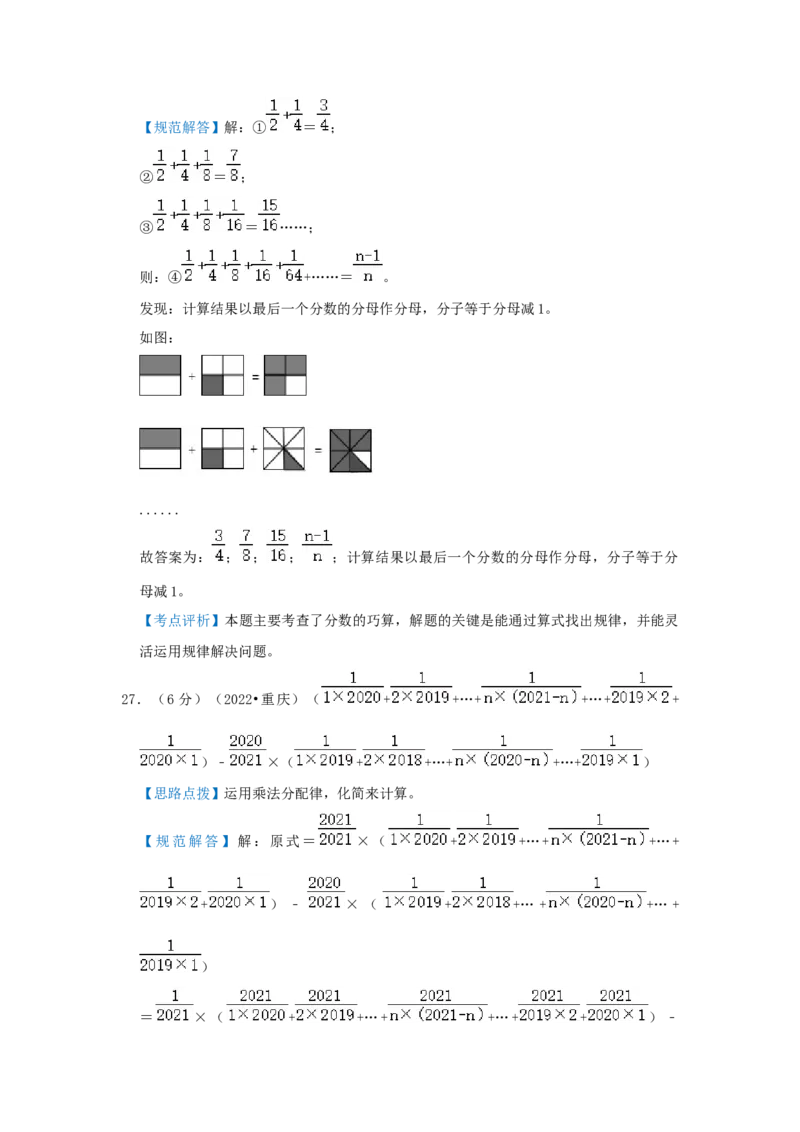
发现: 计算结果以最后一个分数的分母作分母,分子等于分母减 1 。
说明:
【思路点拨】先计算,再观察结果,得出结果的分母与分子关系;根据算式及结果画出
图形即可说明。【规范解答】解:① = ;
② = ;
③ = ……;
则:④ +……= 。
发现:计算结果以最后一个分数的分母作分母,分子等于分母减1。
如图:
......
故答案为: ; ; ; ;计算结果以最后一个分数的分母作分母,分子等于分
母减1。
【考点评析】本题主要考查了分数的巧算,解题的关键是能通过算式找出规律,并能灵
活运用规律解决问题。
27.(6分)(2022•重庆)( + +…+ +…+ +
)﹣ ×( + +…+ +…+ )
【思路点拨】运用乘法分配律,化简来计算。
【规范解答】解:原式= ×( + +…+ +…+
+ ) ﹣ × ( + +… + +… +
)
= ×( + +…+ +…+ + )﹣×( + +…+ +…+ )
= ×(1+ + + +…+ + +…+ + +1+ )﹣ ×
(1+ + + +…+ + +…+1+ )= ×( ×2﹣ ×2)
= ×( ﹣ )
【考点评析】仔细观察,运用相应的运算定律是解决本题的关键