文档内容
高三年级摸底考试试卷
数学 全解全析
【命题双向细目表】
试题难度 预期
题型 题号 分值 考查的主要知识点 试题来源
易 中 难 得分率
选择题 集合交集 原创 .
1 5 √ 085
选择题 复数的运算和概念 原创 .
2 5 √ 085
选择题 导数的几何意义 原创 .
3 5 √ 08
选择题 统计 原创 .
4 5 √ 08
选择题 平面向量的数量积 原创 .
5 5 √ 08
选择题 充分条件与必要条件 原创 .
6 5 √ 075
选择题 古代文化 三角形面积 原创 .
7 5 √ 、 07
选择题 古典概型的概率 原创 .
8 5 √ 055
选择题 函数图象和性质 原创 .
9 5 √ 08
选择题 双曲线性质 定义 原创 .
10 5 √ 、 08
选择题 等差数列的通项公式 性质 原创 .
11 5 √ , 07
选择题 正方体线面 面面位置关系的证明与判定 原创 .
12 5 √ 、 055
填空题 抛物线和圆的方程 原创 .
13 5 √ 08
填空题 二项式定理 原创 .
14 5 √ 07
填空题 四棱台体积的求解 原创 .
15 5 √ 07
填空题 三角恒等变换及函数极值点 原创 .
16 5 √ 05
解答题 正 余弦定理及三角形面积公式 原创 .
17 10 √ 、 08
解答题 等比数列性质及错位相减法求和 原创 .
18 12 √ 075
独立性检验 二项分布的概率计算及其随机
解答题 、 原创 .
19 12 √ 变量的分布列和数学期望 07
解答题 棱锥中的线面位置关系 二面角 原创 .
20 12 √ 、 07
椭圆方程的求法 直线与椭圆位置关系 根与系
解答题 , , 原创 .
21 12 √ 数的关系的应用以及直线与圆恒有交点问题 065
解答题 利用导数求函数单调性 零点 原创 .
22 12 √ 、 055
1.【命题说明】本题依托集合的概念和不等式的基本性质 考查图示法表示集合的关系 交集的定义 解不
, 、 、
等式 考查运算能力和数形结合思想.
,
1
- -【学科素养】本题重在运算与推理 重点考查数学运算和直观想象的核心素养.
,
C 由题可得A x x B xx 由题图可得阴影部分为A B x x .
={|0< <2},={| ≥1}, ∩ ={|1≤ <2}
2.【命题说明】本题依托复数的概念 考查复数的运算和共轭复数的概念 考查运算能力.
, ,
【学科素养】本题重在运算 重点考查数学运算的核心素养.
,
D 因为z i 1 1
= = + i,
1+i 2 2
æ ö
所以z 1 1 z在复平面内对应的点ç1 1÷位于第四象限.
= - i, è ,- ø
2 2 2 2
3.【命题说明】本题依托导数的概念 考查求导法则和导数的几何意义 考查运算能力和数形结合思想.
, ,
【学科素养】本题重点考查数学运算和直观想象的核心素养.
D 函数fx的图象在点P f 处的切线的斜率就是在该点处的导数 即f' 就是切线y x
() (3,(3)) , (3) =-2
的斜率 所以f' 又f 所以f f' .
+7 , (3)=-2, (3)=-2×3+7=1, (3)- (3)=1-(-2)=3
4.【命题说明】本题依托扇形统计图数据 考查了对扇形统计图的理解与应用 考查灵活应用所学知识解答
, ,
实际问题的能力 考查运算能力和数形结合思想.
,
【学科素养】本题重点考查数据分析的核心素养.
C 不妨设 年的高考人数为 则 年的高考人数为 . 年本科达线人数为 年
2021 100, 2022 1502021 50,2022
本科达线人数为 得 年与 年的本科达线人数比为 本科达线人数增加了 故选项
90, 2022 2021 9∶5, 80%,
不正确 选项 正确 年专科达线人数为 年专科达线人数为 所以 年与 年
A , C ;2021 35,2022 45, 2022 2021
的专科达线人数比为 选项 错误 年不上线人数为 年不上线人数也是 不上线的
9∶7, B ;2021 15,2022 15,
人数无变化 选项 错误.
, D
5.【命题说明】本题依托平面向量的概念 考查平面向量数量积的理解与应用 考查运算能力.
, ,
【学科素养】本题重点考查数学运算的核心素养.
A 由已知a 2 2 b m2 a b m
||= (-4)+(-3)=5,||= +1,· =-4 -3,
a b m
所以 ab · -4 -3 3 解得m 或 24 舍去 .
cos<,>=
|
a
||
b
|
=
5×
m2
+1
=-
5
<0, =0 -
7
( )
m
【名师点拨】求得 -4 -3 3之后 不用解方程 可用试值法 将m 24代入 易得m
5×
m2
+1
=-
5
, , , =0,-1,-
7
, =0
符合题意.
6.【命题说明】本题依托不等式 考查充分条件和必要条件的判断 考查灵活应用充分条件和必要条件的定
, ,
义解答问题的能力 考查运算能力.
,
【学科素养】本题重点考查数学运算和逻辑推理的核心素养.
A 因为x 1 x 1
x2
x 且x 充分性成立 所以 x 是 x
+x >1⇒ -1+x >0⇒x >0⇒ >-1 ≠0, , “0< <1” “
+1 +1 +1
1 的充分不必要条件.
+x >1”
+1
7.【命题说明】本题依托古代三角形问题 考查正弦定理在解三角形中的应用 考查二次函数求最值问题
, , ,
考查转化思想.
【学科素养】本题重点考查数学运算和逻辑推理的核心素养.
a a b c c
C 由正弦定理得 + + 得c a 因为b ABC的面积S
A= A B C= A, =2 , = 2,△ =
sin sin +sin +sin 2sin
1
[
a2b2
-
æ
è
ç
a2
+
b2
-
c2ö
ø
÷
2]
=
1
-9
a4
+20
a2
-4,
所以当a2
=
10
,
即a
=
10时
,△
ABC的面积S有最大值为2.
4 2 4 9 3 3
8.【命题说明】本题依托正方体的点 线 面位置关系 考查古典概型的概率求解 考查运算能力和空间想象能力.
、 、 , ,
【学科素养】本题重点考查数学运算和直观想象的核心素养.
D 从正方体的 个顶点和中心中任取 个 有n 4 个结果 个点恰好构成三棱锥分两种情况
8 4 , =C9=126 ,4 :
2
- -从正方体的 个顶点中取 个点 共有 4 个结果 在同一个平面的有m 个 构成三棱
① 8 4 , C8=70 , =6+6=12 ,
锥有 个 从正方体的 个顶点中取 个与中心构成三棱锥有 3 个 故从正方体的 个
70-12=58 ;② 8 3 6C4+8=32 , 8
顶点和中心中任选 个 则这 个点恰好构成三棱锥的个数为 故所求概率P 90 5.
4 , 4 58+32=90, = =
126 7
9.【命题说明】本题依托函数图象 考查函数性质 函数单调性 奇偶性 极值等问题 考查数形结合思想.
, , 、 、 ,
【学科素养】本题重点考查逻辑推理和数学抽象的核心素养.
AC 对于 f x 4 x2 4x2 fx为偶函数 图象为开口向上的抛物线 f 4 与题
A,(- )= (- )= = () , ,(1)= <1,
5 5 5
干图象相符 对于 fx x4 为偶函数 但f 与题干图象不相符 对于 f x x x
; B,()= , (1)=1, ; C,(- )=(- )sin(- )
x x fx为偶函数 由f'x x x x当 x π时f'x fx单调递增 且f
= sin = () , ()=sin + cos , 0< < , ()>0,() , (1)=
2
x
与题干图象相符 对于 f x - fx为奇函数 与题干图象不相符.
sin1<1, ; D,(- )= x2 =- () ,
(- )+1
10.【命题说明】本题依托双曲线方程 考查双曲线性质 定义 考查数形结合思想.
, 、 ,
【学科素养】本题重点考查数学运算和逻辑推理的核心素养.
ABD 由双曲线方程知 离心率为e
c a2
+3 解得a 故Cx2
y2
实半轴长为 实轴
: =a= a =2, =1, : - =1, 1,
3
长为 a 正确 因为可求得双曲线渐近线方程为y x故一条渐近线方程为y x 正确
2 =2,A ; =± 3 , = 3 ,B ;
由于P可能在C的不同分支上 则有 PF PF 错误 焦距为 c a2 b2 正确.
, || 1|-| 2||=2,C ; 2=2 + =4,D
11.【命题说明】本题依托等差数列概念 考查等差数列的通项公式 前n项和的性质 考查基本不等式综合
, 、 ,
应用 考查转化思想.
,
【学科素养】本题重点考查数学运算和数学抽象的核心素养.
ACD 设等差数列的公差为d因为a a 所以a a d所以d 则a a a 故 正确
, 1= 5, 1= 1+4 , =0, 1= 2=…= n, A ;
因为a a 所以a d a d所以d a 为递增数列 但S S S 不一定成立 如a
5> 3, 1+4 > 1+2 , >0,{n} , 1< 2<…< n , 1
=-2,
a
2=-1,
a
3=0,
S
1=-2,
S
2=-3,
S
3=-3,
故
B
不正确
;
因为a2
1+
a2
5≥2
æ
è
ç a 1+ a 5 ö
ø
÷ 2
=2
a2
3=8,
当
2
{a a d {d
且仅当a a 时取等号 故 正确 因为 4= 1+3 =8,解得 =-1,则a a d
1= 5=2 , C ; a a d a 12= 4+8 =8-8=0,
8= 1+7 =4, 1=11,
a a
得S 1+ 12 故 正确.
12= ×12=66, D
2
【知识总结】结论 等差 等比数列的性质 若m n p q tmnpqt N*
:(1) 、 : + = + =2( ,,,,∈ ),
若a 为等差数列 则有a a a a a
① {n} , m+ n= p+ q=2t;
②
若
{
a
n}
为等比数列
,
则有a
m·
a
n=
a
p·
a
q=
a
t
2.
设等差数列a 的公差为d当d 时 为常数列 当d 时 递增 当d 时 递减.
(2) {n} , =0 , ; >0 , ; <0 ,
12.【命题说明】本题依托正方体 考查线面 面面位置关系的证明与判定 异面直线所成角的定义等问题
, 、 , ,
考查数形结合与转化思想.
【学科素养】本题重点考查数学运算 直观想象和逻辑推理的核心素养.
、
BC 因为AC AC 所以直线AC 与BC所成的角为 故 错误
∥ 1 1, 1 1 45°, A ;
因为BD 平面ACCA 故BD 平面ACE 故 正确
⊥ 1 1, ⊥ , B ;
当点E在A 处时 平面ABE 平面CCDD
1 , ∥ 1 1 ,
所以存在点E 使得平面ABE 平面CCDD 故 正确.
, ∥ 1 1 , C
如图 过点E作MN AB 则MN为平面ABE与平面CDE的交线
, ∥ 1 1, ,
在正方体中 AB 平面BCCB 所以MN 平面BCCB 所以BN MN
,1 1⊥ 1 1, ⊥ 1 1, ⊥ ,
CN MN 所以 BNC即为平面ABE与平面CDE所成的夹角
⊥ , ∠ ,
3
- -因为点N一定在以BC为直径的圆外
,
所以 BNC 所以不存在点E 使得平面ABE 平面CDE 故 错误.设正方体的棱长为 BN
∠ <90°, , ⊥ , D ( 1,1
x则 BBN x CCN x
= , tan∠ 1 = ,tan∠ 1 =1- ,
x x
所以 BNC BBN CCN +(1- ) 1 1
tan∠ =tan(∠ 1 +∠ 1 )= 1- x (1- x ) =x2 - x +1 =æ çx 1 ö ÷ 2 3 ,
è - ø +
2 4
当x 1时 BNC取得最大值 为4 此时 BNC为锐角 故 错误.
= ,tan∠ , , ∠ , D )
2 3
13.【命题说明】本题依托抛物线和圆的方程 突出考查了抛物线性质和圆的切线 试题设计灵活 强调综合
, , ,
运用所学知识来解决问题的能力.
【学科素养】本题重在运算 重点考查数学运算和直观想象的核心素养.
,
【解析】抛物线y2 x的准线为x 圆C x a2 y2 的圆心为a 半径r 与准线x
=4 =-1, :(- )+ =1 (,0), =1, =
相切 得a 或 .
-1 , =-2 0
答案: 或
-2 0
14.【命题说明】本题依托二项式定理 突出考查利用二项式展开式的通项求系数 考查学生对这些知识的
, ,
理解掌握水平 试题设计灵活 强调综合运用所学知识来解决问题的能力.
, ,
【学科素养】本题重在运算 重点考查数学运算的核心素养.
,
【解析】令x =0⇒ a 0=-1, 由题得 ( x -1) 5 的展开式的通项为T r +1=C r 5 x5- r (-1) r ,
令 r 得r 令 r 得r
5- =2, =3, 5- =3, =2,
所以a 3 3 2 2
3=C5(-1)+C5(-1)=0,
所以a a .
0+ 3=-1
答案:
-1
15.【命题说明】本题依托四棱台和四棱锥 突出考查四棱台体积的求解 考查学生对四棱台知识的理解掌
, ,
握水平 试题设计灵活 强调综合运用所学知识来解决问题的能力.
, ,
【学科素养】本题重在运算 重点考查数学运算和直观想象的核心素养.
,
【解析】方法一 由题意 设点E到平面ABCD的距离为h 由四边形ABCD面积为S
2
得
: , , =(4 3)=48,
四棱锥E-ABCD的体积为 1hS 1 h得h .
48= = ×48 , =3
3 3
所以棱台体积为V
=
1h
(
S上
+
S上S下
+
S下)= 1
×3×(48+ 48×243+243)=399
.
3 3
方法二 由题意 设点E到平面ABCD的距离为h 由四边形ABCD面积为S
2
得四棱锥
: , , =(4 3)=48,
E-ABCD的体积为 1hS 1 h 得h .由棱台定义知 延长EAFBGCHD交于一点 图
48= = ×48 , =3 , , , , (
3 3
略 设为P 设棱锥P-ABCD的高为x
), , ,
x AB
则棱锥P-EFGH的高为x 由三角形相似可得 4 得x 12 于是棱台体积V 1 x
+3, x =EF= , = , = (+
+3 9 5 3
3)
S下
-
1xS上
=
1
×
27
×243-
1
×
12
×48=399
.
3 3 5 3 5
答案:
399
16.【命题说明】本题依托三角函数解析式 突出考查利用正弦型函数在区间上的极值点个数判断正弦型函
,
数的基本性质 考查三角变换公式 强调综合运用所学知识来解决问题的能力.
, ,
【学科素养】本题重在运算 重点考查了数学抽象和逻辑推理的核心素养.
,
æ ö ( ) æ ö
【解析】fx ωx çωx π÷ 3 ωx 3 ωx 3 ωx 1 ωx çωx π÷
()=sin +sinè + ø= sin + cos =3 sin + cos =3sinè + ø,
3 2 2 2 2 6
[ ]
当x 时ωx π πω π
∈[0,π] , + ∈ ,π+ ,
6 6 6
4
- -[ ]
令t ωx π 则t πω π
= + , ∈ ,π+ ,
6 6 6
æ ö
作出函数y tçπ t ω πω ÷的图象如图所示
= 3sin è ≤ ≤ π+ ,>0ø :
6 6
由于函数fx在 上有且仅有 个极值点
() [0,π] 3 ,
则5 ω π 7 解得7 ω 10.
π≤ π+ < π, ≤ <
2 6 2 3 3
[ ö
答案:7 10÷
, ø
3 3
[ ]
【名师指点】解本题的关键在于换元t ωx π 将问题转化为函数y t在区间 πω π 上的
= + , = 3sin ,π+
6 6 6
极值点个数问题 数形结合来求解.
,
17.【命题说明】本题考查利用正 余弦定理解三角形的方法 考查三角变换公式及对三角形面积公式的理
、 ,
解与应用能力 强调综合运用所学知识来解决问题的能力.
,
【学科素养】本题重在运算 重点考查数学运算和逻辑推理的核心素养.
,
【分析】 选择 利用正弦定理边角互化 结合余弦定理可求得 A的值 结合角A的取值范围可求
(1) ①: , tan ,
得角A的值
;
选择 由正弦定理 余弦定理可求得 A的值 结合角A的取值范围可求得角A的值
②: 、 cos , ;
利用余弦定理可求得bc的值 结合三角形面积公式可得出 ABC的面积.
(2) , △
【解析】 选择 因为b2 c2 a2 ac B
(1) ①: + - =2 3 sin ,
由余弦定理可得 bc A ac B
2 cos =2 3 sin ,
所以结合正弦定理可得 B A A B. ………………………………………………… 分
sin cos = 3sin sin 3
因为B 则 B
∈(0,π), sin >0,
所以 A A 即 A 3
cos = 3sin , tan = ,
3
因为A 所以A π …………………………………………………………………………… 分
∈(0,π), = ; 5
6
选择 因为 2B 2C 2A B C
②: sin +sin -sin = 3sin sin ,
由正弦定理得b2 c2 a2 bc ……………………………………………………………………… 分
+ - = 3 , 3
由余弦定理得 A
b2
+
c2
-
a2
3.
cos = bc =
2 2
因为A 所以A π …………………………………………………………………………… 分
∈(0,π), = ; 5
6
由 知A π 又已知a b c
(2) (1) = , =8,+ =10,
6
由余弦定理得a2 b2 c2 bc A b c2 bc ……………………………………… 分
, = + -2 cos =(+ )-(2+ 3) , 7
即 bc所以bc 36
64=100-(2+ 3) , = ,
2+ 3
所以 ABC的面积为1bc A 1bc π . ………………………………………… 分
△ sin = sin =9(2- 3) 10
2 2 6
5
- -18.【命题说明】本题依托等比数列概念 突出考查数列的求和方法 考查学生对错位相减法的理解与应用
, ,
能力 强调综合运用所学知识来解决问题的能力.
,
【学科素养】本题重在运算 重点考查数学运算和逻辑推理的核心素养.
,
【分析】 根据S S 得到aq的值 得到a 的通项公式.
(1) 3=14,6=126, 1, , {n}
首先根据 得到b n a 再利用错位相减法求T 即可.
(2) (1) n=(-1)n, n
【解析】 设等比数列a 的公比为q显然q 由S S
(1) {n} , ≠1, 3=14,6=126,
得S
a
1(1-
q3
) S
a
1(1-
q6
) ………………………………………………………… 分
3= q =14,6= q =126, 3
1- 1-
相除得 q3 得q 所以a
1+ =9, =2, 1=2,
所以数列a 是以 为首项 以 为公比的等比数列 即a n …………………………………… 分
{n} 2 , 2 , n=2; 6
由 可得b n a n n
(2) (1) n=(-1)n=(-1)2,
所以T n=1×2 2 +2×2 3 +…+( n -2)×2 n -1 +( n -1)×2 n ……①,
1T n=1×2+2×2 2 +…+( n -2)×2 n -2 +( n -1)×2 n -1 ……②, …………………………………… 9 分
2
②-①, 得 - 1T n=2+2 2 +…+2 n -2 +2 n -1 -( n -1)×2 n ,
2
n
得
-
1T
n=
2(1-2 -1 )
-(
n
-1)×2
n
,
2 1-2
所以T
n=4+(
n
-2)×2
n +1.……………………………………………………………………………
12
分
【方法指导】本题主要考查数列的求和 常见的数列求和方法如下
, :
.公式法 直接利用等差 等比数列的求和公式计算即可
1 : 、 ;
.分组求和法 把需要求和的数列分成熟悉的数列 再求和即可
2 : , ;
.裂项相消法 通过把数列的通项公式拆成两项之差 再求和即可
3 : , ;
.错位相减法 当数列的通项公式由一个等差数列和一个等比数列的乘积构成时 可使用此方法求和.
4 : ,
19.【命题说明】本题依托数据统计 频率分布 突出考查列联表的填写
χ2
的计算 二项分布的概率计算公
、 , 、 、
式及其随机变量的分布列和数学期望 强调综合运用所学知识来解决问题的能力.
,
【学科素养】本题重在运算 重点考查数学运算 数据分析的核心素养.
, 、
【解析】
(1)
项目 晨读不合格 晨读合格 合计
高二
25 75 100
高三
15 85 100
合计
40 160 200
…………………………………………………………………………………………………………… 分
2
2
χ2 = 200×(25×85-15×75) =3 . 125<3 . 841= x 0 . 05,
100×100×40×160
所以依据α . 的独立性检验 不能认为 晨读合格 与年级有关联. …………………………… 分
=005 , “ ” 5
题表中学生晨读合格的概率为160 4
(2) = ,
200 5
æ ö
所以 ξ ~ B è ç 2, 4 ø ÷ , ……………………………………………………………………………………… 7 分
5
所以P ( ξ =0)=C 0 2· æ è ç4 ö ø ÷ 0 · æ è ç1 ö ø ÷ 2 = 1 ,
5 5 25
æ ö1 æ ö1
P ( ξ =1)=C 1 2·è ç4 ø ÷ ·è ç1 ø ÷ = 8 ,
5 5 25
6
- -P ( ξ =2)=C 2 2· æ è ç4 ö ø ÷ 2 · æ è ç1 ö ø ÷ 0 = 16 , ………………………………………………………………… 10 分
5 5 25
的分布列为
ξ
ξ
0 1 2
P 1 8 16
25 25 25
…………………………………………………………………………………………………………… 分
11
所以Eξ 4 8 ………………………………………………………………………………… 分
()=2× = 12
5 5
或Eξ 1 8 16 8.……………………………………………………………… 分
()=0× +1× +2× = 12
25 25 25 5
20.【命题说明】本题依托四棱锥 考查棱锥中的线面位置关系及求二面角 强调综合运用所学知识来解决
, ,
问题的能力.
【学科素养】本题重在运算 联想与推理 重点考查数学运算 直观想象和逻辑推理的核心素养.
、 , 、
【分析】 设AB AD DC 可得AC BC 利用平面PCB 平面ABCD 可得AC 平面PCB
(1) =2 =2 =2, ⊥ , ⊥ , ⊥ ,
则AC PB
⊥ ;
取BC的中点O为坐标原点 以OP的方向为z轴正方向 过点O分别作AB和AD的平行线 分别
(2) , , ,
为x轴和y轴 建立空间直角坐标系O-xyz 分别求得平面ABP的法向量和平面ACP的法向量 进而
, , ,
利用数量积求解即可.也可以直接寻找两平面所成角的平面角 在三角形中运用余弦定理求解.
,
【解析】 由题意 设AB AD DC 又AB DCAB AD 得AC BC 又AB
(1) , =2 =2 =2, ∥ , ⊥ , = = 2, =2,
所以AC BC …………………………………………………………………………………………… 分
⊥ , 2
又平面PCB 平面ABCD CB且平面PCB 平面ABCDAC 平面ABCD
∩ = , ⊥ , ⊂ ,
所以AC 平面PCB 故AC PB. …………………………………………………………………… 分
⊥ , ⊥ 3
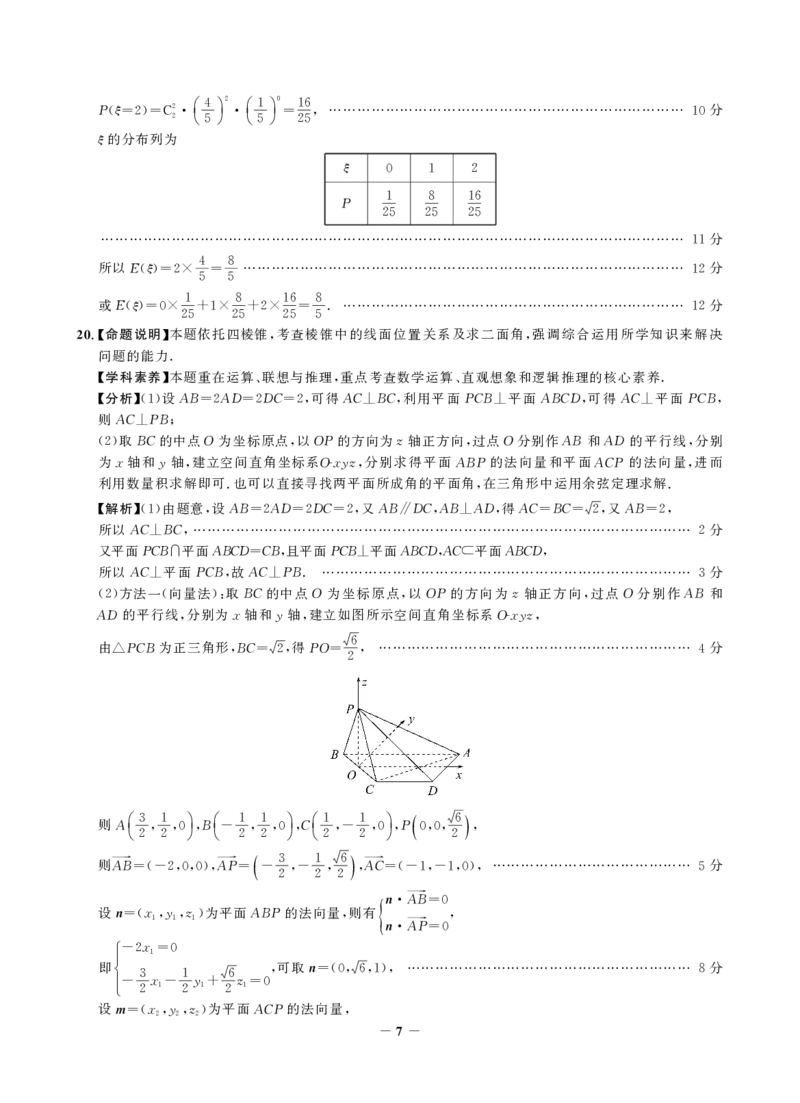
方法一 向量法 取BC的中点O为坐标原点 以OP的方向为z轴正方向 过点O分别作AB和
(2) ( ): , ,
AD的平行线 分别为x轴和y轴 建立如图所示空间直角坐标系O-xyz
, , ,
由 PCB为正三角形 BC 得PO 6 ………………………………………………………… 分
△ , = 2, = , 4
2
æ ö æ ö æ ö ( )
则Aç3 1 ÷ Bç 1 1 ÷ Cç1 1 ÷ P 6
è , ,0ø, è- , ,0ø, è ,- ,0ø, 0,0, ,
2 2 2 2 2 2 2
( )
则AB→ AP→ 3 1 6 AC→ …………………………………… 分
=(-2,0,0), = - ,- , , =(-1,-1,0), 5
2 2 2
{n AB→
设n x y z 为平面ABP的法向量 则有 · =0
=(1,1,1) , n AP→ ,
· =0
ì ïï-2 x
1=0
即í 可取n …………………………………………………… 分
ïï 3x 1y 6z , =(0,6,1), 8
î- 1- 1+ 1=0
2 2 2
设m x y z 为平面ACP的法向量
=(2,2,2) ,
7
- -{m AC→
则有 · =0
m AP→ ,
· =0
ì ïï- x
2-
y
2=0 ( )
即í 可取m 6 ……………………………………………… 分
î ïï - 3x 2- 1y 2+ 6z 2=0 , = 1,-1, 3 , 10
2 2 2
6
n m - 6+
所以 nm · 3 7
cos<,>=n m = =- ,
||| | 8 7
7×
3
设二面角B-PA-C的平面角为α
,
( )
则 α nm 2 7 2 42
sin = 1-(cos<,>)= 1- - = ,
7 7
故二面角B-PA-C的正弦值为 42.………………………………………………………………… 分
12
7
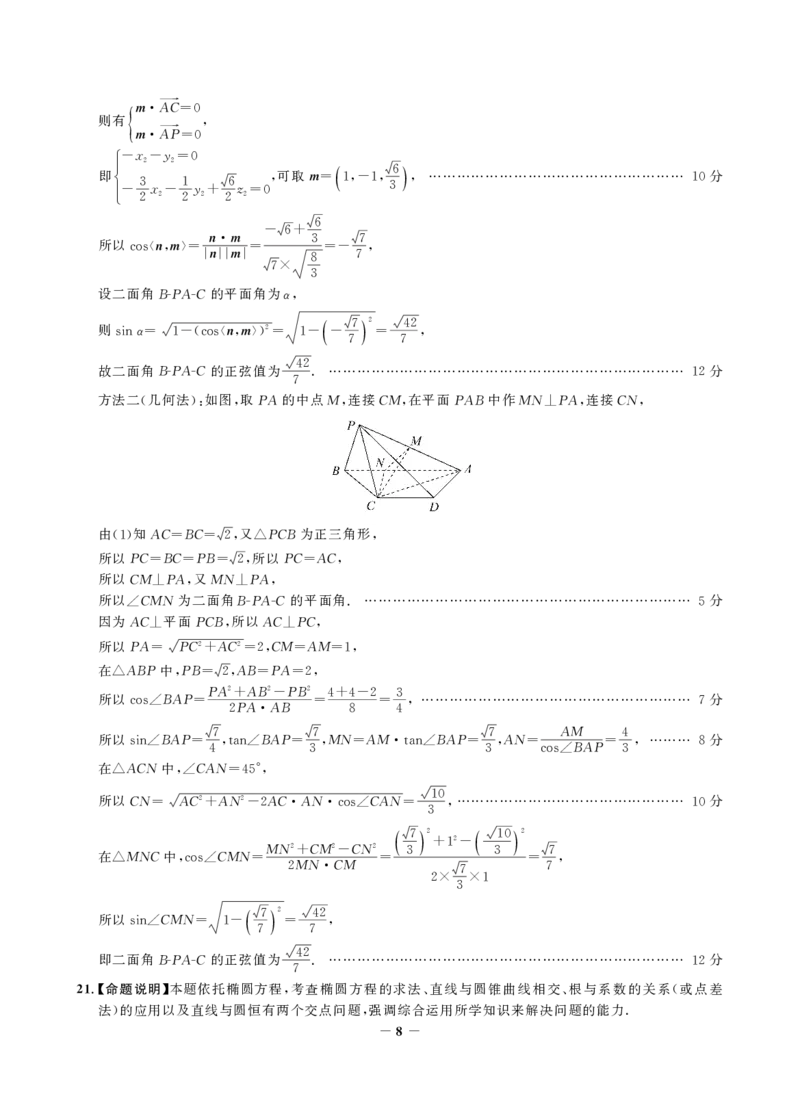
方法二 几何法 如图 取PA的中点M 连接CM 在平面PAB中作MN PA 连接CN
( ): , , , ⊥ , ,
由 知AC BC 又 PCB为正三角形
(1) = = 2, △ ,
所以PC BC PB 所以PC AC
= = = 2, = ,
所以CM PA 又MN PA
⊥ , ⊥ ,
所以 CMN为二面角B-PA-C的平面角.…………………………………………………………… 分
∠ 5
因为AC 平面PCB 所以AC PC
⊥ , ⊥ ,
所以PA PC2 AC2 CM AM
= + =2, = =1,
在 ABP中 PB AB PA
△ , = 2, = =2,
所以 BAP
PA2
+
AB2
-
PB2
4+4-2 3 ………………………………………………… 分
cos∠ = PA AB = = , 7
2 · 8 4
AM
所以 BAP 7 BAP 7MN AM BAP 7AN 4 ……… 分
sin∠ = ,tan∠ = , = ·tan∠ = , = BAP= , 8
4 3 3 cos∠ 3
在 ACN中 CAN
△ ,∠ =45°,
所以CN AC2 AN2 AC AN CAN 10 ………………………………………… 分
= + -2 · ·cos∠ = , 10
3
( ) ( )
2 2
7 2 10
在 MNC中 CMN
MN2
+
CM2
-
CN2
3
+1-
3 7
△ ,cos∠ = MN CM = = ,
2 · 7 7
2× ×1
3
( )
所以 CMN 7 2 42
sin∠ = 1- = ,
7 7
即二面角B-PA-C的正弦值为 42.………………………………………………………………… 分
12
7
21.【命题说明】本题依托椭圆方程 考查椭圆方程的求法 直线与圆锥曲线相交 根与系数的关系 或点差
, 、 、 (
法 的应用以及直线与圆恒有两个交点问题 强调综合运用所学知识来解决问题的能力.
) ,
8
- -【学科素养】本题重在运算 联想与推理 重点考查数学运算 直观想象和逻辑推理的核心素养.
、 , 、
【分析】 根据题意 NFF 的面积为 结合四边形MFNF 的四条边的平方和为 即 b2 c2
(1) △ 1 2 3, 2 1 16, 4( + )
求出ab即可得结果
=16, , ;
联立直线与椭圆的方程 结合根与系数的关系 或点差法 根据中点坐标公式化简 列出线段AB的
(2) , ( ), ,
垂直平分线方程 判断定点在圆内即可得结果.
,
【解析】 由 NFF 的面积为 得1 c b ……………………………………………… 分
(1) △ 1 2 3, ×2× = 3, 2
2
又四边形MFNF 的四条边的平方和为
2 1 16,
所以a2 b2 c2 或a2 b2 c2
=4, =3, =1 =4, =1, =3,
即椭圆C的方程为
x2 y2
或
x2
y2 . ………………………………………………………… 分
+ =1 + =1 4
4 3 4
方法一 设Ax y Bx y 由于a b 得椭圆C的方程为
x2 y2
……………… 分
(2) : (1,1),(2,2), > >1, + =1, 5
4 3
设直线l的方程为y kx m 结合图形 图略 知 当斜率k 时 线段AB的中点H在y轴上 不在直
= + , ( ) , =0 , ,
线x 1上 故k
= , ≠0,
2
{x2 y2
由 + =1
4 3 ,
y kx m
= +
得 k2x2 kmx m2 ………………………………………………………………… 分
(3+4 ) +8 +4 -12=0, 7
由Δ k2m2 k2 m2 m2 k2 得m2 k2.
=64 -4(3+4 )(4 -12)=-48( -4 -3)>0, <3+4
km
由x x 8 …………………………………………………………………………………… 分
1+ 2=- k2, 9
3+4
km
设线段AB的中点H为x y 得x 4 1
(0,0), 0=- k2= ,
3+4 2
即 k2 km
3+4 =-8 ,
所以y kx m 3.……………………………………………………………………………… 分
0= 0+ =-k 10
8
æ ö
所以线段AB的垂直平分线的方程为y 3 1çx 1÷.
+k=-kè - ø
8 2
æ ö
即y 1çx 1÷
=-kè - ø,
8
æ ö
故线段AB的垂直平分线恒过点ç1 ÷.…………………………………………………………… 分
è ,0ø 11
8
因为 æ è ç1 ö ø ÷ 2 +0 2 = 1 < 1 ,
8 64 4
æ ö
故点
è
ç1
,0ø
÷在圆x2
+
y2
=
1内
,
8 4
所以线段AB的垂直平分线与圆x2 y2 1恒有两个交点.……………………………………… 分
+ = 12
4
方法二 由于a b 得椭圆C的方程为
x2 y2
……………………………………………… 分
: > >1, + =1, 5
4 3
设直线l的方程为y kx m 结合图形 图略 知 当斜率k 时 线段AB的中点H在y轴上 不在直
= + , ( ) , =0 , ,
线x 1上 故k
= , ≠0,
2
æ ö
ì
ï ï
x2
1 +
y2
1 =1,①
设Ax y Bx y Hç1y÷ AB点代入椭圆方程得í4 3 ……………………… 分
(1,1),(2,2), è
2
,0ø, ,
î
ï ïx2
2
y2
2
7
+ =1,②
4 3
9
- -得 1 x x x x 1y y y y ………………………………………… 分
①-② , (1+ 2)(1- 2)+ (1+ 2)(1- 2)=0, 8
4 3
y y
将x x y y y 1- 2 k代入上式化简 得y 3 ……………………………… 分
1+ 2=1,1+ 2=20,x x= , , 0=-k, 10
1- 2 8
æ ö
所以线段AB的垂直平分线的方程为y 3 1çx 1÷.
+k=-kè - ø
8 2
æ ö
即y 1çx 1÷
=-kè - ø,
8
æ ö
故线段AB的垂直平分线恒过点ç1 ÷.…………………………………………………………… 分
è ,0ø 11
8
因为 æ è ç1 ö ø ÷ 2 +0 2 = 1 < 1 , 故点 æ è ç1 ,0 ö ø ÷在圆x2 + y2 = 1内 ,
8 64 4 8 4
所以线段AB的垂直平分线与圆x2 y2 1恒有两个交点.……………………………………… 分
+ = 12
4
22.【命题说明】本题依托指数函数和对数函数 考查利用导数求函数单调区间 考查利用导数研究函数的
, ,
零点存在性问题 强调综合运用所学知识来解决问题的能力.
,
【学科素养】本题重在运算与推理 重点考查数学运算和逻辑推理的核心素养.
,
a x a
【解析】 由题意可得函数fx的定义域为 f'x - …………………… 分
(1) () (0,+∞), ()=1-x= x , 2
当a 时 令f'x 得x a
>0 , ()>0, > ,
所以fx在a 上单调递增 令f'x 得 x a
() (,+∞) ; ()<0, 0< < ,
所以fx在 a上单调递减 ………………………………………………………………………… 分
() (0,) ; 4
当a 时 因为f'x 恒成立
<0 , ()>0 ,
所以fx在 上单调递增 …………………………………………………………………… 分
() (0,+∞) ; 5
gx xx a x x xx a xx x ………………………………………………… 分
(2)()= e- (ln + )= e-ln(e)(>0), 6
令t xx 则t' x x 在x 时恒成立
= e, =(+1)e>0 >0 ,
所以t xx在x 时单调递增 且t
= e >0 , ∈(0,+∞),
所以gx xx a xx 有两个零点等价于ft t a t有两个零点.………………………… 分
()= e-ln(e) ()= -ln 7
因为a 由 知ft在a 上单调递增 在 a上单调递减
>e, (1) ,() (,+∞) , (0,) ,
所以ft fa a a a a a
()min= ()= -ln = (1-ln ),
因为a 所以fa .……………………………………………………………………………… 分
>e, ()<0 9
下面证明当a 时f a a a2
>e ,(e)=e- >0,
设hx x x2 则h'x x x
()=e- , ()=e-2 ,
令mx x x又m'x x
()=e-2 , ()=e-2,
当x 时 m'x x 恒成立 所以mx单调递增
>e , ()=e-2>0 , () ,
得h'x x x e
()=e-2 >e-2e>0,
故hx x x2 在 上单调递增
()=e- (e,+∞) ,
得 x x2 e 2 即f a a a2
e- >e-e>0, (e)=e- >0,
又因为f …………………………………………………………………………………… 分
(1)=1>0, 11
所以ft在 a a a 上各存在一个零点
() (1,),(,e) ,
所以a 时 函数ft有且仅有两个零点
>e , () ,
即当a 时 函数gx有且仅有两个零点.………………………………………………………… 分
>e , () 12
10
- -