文档内容
五年(2019-2023)年高考真题分项汇编
专题 05 立体几何(选填题)
立体几何在文科数高考中属于重点知识点,难度中等。包含题型主要是
1 空间几何体基本性质及表面积体积
2 空间几何题三视图
4 空间几何体内切球外接球的应用
5 空间几何体性质综合应用
考点 01 空间几何体基本性质及表面积体积
1.(2023·年全国甲卷)在三棱锥 中, 是边长为2的等边三角形, ,
则该棱锥的体积为( )
A.1 B. C.2 D.3
1.A【分析】证明 平面 ,分割三棱锥为共底面两个小三棱锥,其高之和为AB得解.
【详解】取 中点 ,连接 ,如图,
是边长为2的等边三角形, ,
,又 平面 , ,
平面 ,
又 , ,
故 ,即 ,
所以 ,
1故选:A
2.(2023·北京·统考高考真题)坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以
勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两
个面是全等的等腰三角形.若 ,且等腰梯形所在的平面、等腰三角形所在的平面
与平面 的夹角的正切值均为 ,则该五面体的所有棱长之和为( )
A. B.
C. D.
2.C
【分析】先根据线面角的定义求得 ,从而依次求 , , , ,再把所
有棱长相加即可得解.
【详解】如图,过 做 平面 ,垂足为 ,过 分别做 , ,垂足分别为 ,
,连接 ,
由题意得等腰梯形所在的面、等腰三角形所在的面与底面夹角分别为 和 ,
所以 .
因为 平面 , 平面 ,所以 ,
因为 , 平面 , ,
所以 平面 ,因为 平面 ,所以 ,.
同理: ,又 ,故四边形 是矩形,
所以由 得 ,所以 ,所以 ,
所以在直角三角形 中,
在直角三角形 中, , ,
2又因为 ,
所有棱长之和为 .
故选:C
3.(2022·全国乙卷)在正方体 中,E,F分别为 的中点,则( )
A.平面 平面 B.平面 平面
C.平面 平面 D.平面 平面
3.A
【分析】证明 平面 ,即可判断A;如图,以点 为原点,建立空间直角坐标系,设 ,分
别求出平面 , , 的法向量,根据法向量的位置关系,即可判断BCD.
【详解】解:在正方体 中,
且 平面 ,
又 平面 ,所以 ,
因为 分别为 的中点,
所以 ,所以 ,
又 ,
所以 平面 ,
又 平面 ,
所以平面 平面 ,故A正确;
选项BCD解法一:
如图,以点 为原点,建立空间直角坐标系,设 ,
则 ,
,
则 , ,
设平面 的法向量为 ,
则有 ,可取 ,
同理可得平面 的法向量为 ,
平面 的法向量为 ,
3平面 的法向量为 ,
则 ,
所以平面 与平面 不垂直,故B错误;
因为 与 不平行,
所以平面 与平面 不平行,故C错误;
因为 与 不平行,
所以平面 与平面 不平行,故D错误,
故选:A.
选项BCD解法二:
解:对于选项B,如图所示,设 , ,则 为平面 与平面 的交线,
在 内,作 于点 ,在 内,作 ,交 于点 ,连结 ,
则 或其补角为平面 与平面 所成二面角的平面角,
由勾股定理可知: , ,
底面正方形 中, 为中点,则 ,
由勾股定理可得 ,
从而有: ,
4据此可得 ,即 ,
据此可得平面 平面 不成立,选项B错误;
对于选项C,取 的中点 ,则 ,
由于 与平面 相交,故平面 平面 不成立,选项C错误;
对于选项D,取 的中点 ,很明显四边形 为平行四边形,则 ,
由于 与平面 相交,故平面 平面 不成立,选项D错误;
故选:A.
4.(2022·全国甲卷)在长方体 中,已知 与平面 和平面 所成的角均为
,则( )
A. B.AB与平面 所成的角为
C. D. 与平面 所成的角为
4.D
【分析】根据线面角的定义以及长方体的结构特征即可求出.
【详解】如图所示:
5不妨设 ,依题以及长方体的结构特征可知, 与平面 所成角为 ,
与平面 所成角为 ,所以 ,即 , ,解得
.
对于A, , , ,A错误;
对于B,过 作 于 ,易知 平面 ,所以 与平面 所成角为 ,因为
,所以 ,B错误;
对于C, , , ,C错误;
对于D, 与平面 所成角为 , ,而 ,所以
.D正确.
故选:D.
5.(2021·全国乙卷)在正方体 中,P为 的中点,则直线 与 所成的角为( )
A. B. C. D.
5.D
【分析】平移直线 至 ,将直线 与 所成的角转化为 与 所成的角,解三角形即可.
【详解】
6如图,连接 ,因为 ∥ ,
所以 或其补角为直线 与 所成的角,
因为 平面 ,所以 ,又 , ,
所以 平面 ,所以 ,
设正方体棱长为2,则 ,
,所以 .
故选:D
6.(2021·年全国新高考Ⅰ卷)已知圆锥的底面半径为 ,其侧面展开图为一个半圆,则该圆锥的母线长
为( )
A. B. C. D.
6.B
【分析】设圆锥的母线长为 ,根据圆锥底面圆的周长等于扇形的弧长可求得 的值,即为所求.
【详解】设圆锥的母线长为 ,由于圆锥底面圆的周长等于扇形的弧长,则 ,解得 .
故选:B.
7.(2021年全国高考Ⅱ卷)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A. B. C. D.
7.D
【分析】由四棱台的几何特征算出该几何体的高及上下底面面积,再由棱台的体积公式即可得解.
【详解】作出图形,连接该正四棱台上下底面的中心,如图,
7因为该四棱台上下底面边长分别为2,4,侧棱长为2,
所以该棱台的高 ,
下底面面积 ,上底面面积 ,
所以该棱台的体积 .
故选:D.
8.(2021·年全国高考Ⅰ卷)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,
以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与
底面正方形的边长的比值为( )
A. B. C. D.
8.C
【分析】设 ,利用 得到关于 的方程,解方程即可得到答案.
【详解】如图,设 ,则 ,
由题意 ,即 ,化简得 ,
解得 (负值舍去).
故选:C.
8【点晴】本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题.
9.(2019·年全国高考Ⅰ卷)设 , 为两个平面,则 的充要条件是
A. 内有无数条直线与 平行
B. 内有两条相交直线与 平行
C. , 平行于同一条直线
D. , 垂直于同一平面
9.B
【分析】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平
行的判定定理与性质定理即可作出判断.
【详解】由面面平行的判定定理知: 内两条相交直线都与 平行是 的充分条件,由面面平行性质
定理知,若 ,则 内任意一条直线都与 平行,所以 内两条相交直线都与 平行是 的必要
条件,故选B.
【点睛】面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:
“若 ,则 ”此类的错误.
10.(2019·全国高考Ⅲ卷)如图,点 为正方形 的中心, 为正三角形,平面 平面
是线段 的中点,则
A. ,且直线 是相交直线
B. ,且直线 是相交直线
C. ,且直线 是异面直线
D. ,且直线 是异面直线
910.B
【解析】利用垂直关系,再结合勾股定理进而解决问题.
【详解】如图所示, 作 于 ,连接 ,过 作 于 .
连 , 平面 平面 .
平面 , 平面 , 平面 ,
与 均为直角三角形.设正方形边长为2,易知 ,
. ,故选B.
【点睛】本题考查空间想象能力和计算能力, 解答本题的关键是构造直角三角形.
三、填空题
11.(2023全国高考Ⅰ卷)在正四棱台 中, ,则该棱台的体积
为 .
11. /
【分析】结合图像,依次求得 ,从而利用棱台的体积公式即可得解.
【详解】如图,过 作 ,垂足为 ,易知 为四棱台 的高,
因为 ,
10则 ,
故 ,则 ,
所以所求体积为 .
故答案为: .
12.(2023年全国高考Ⅱ卷)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为
2,高为3的正四棱锥,所得棱台的体积为 .
12.
【分析】方法一:割补法,根据正四棱锥的几何性质以及棱锥体积公式求得正确答案;方法二:根据台体
的体积公式直接运算求解.
【详解】方法一:由于 ,而截去的正四棱锥的高为 ,所以原正四棱锥的高为 ,
所以正四棱锥的体积为 ,
截去的正四棱锥的体积为 ,
所以棱台的体积为 .
方法二:棱台的体积为 .
故答案为: .
13.(2020·海南·高考真题)已知正方体ABCD-A B C D 的棱长为2,M、N分别为BB 、AB的中点,则三棱
1 1 1 1 1
锥A-NMD 的体积为
1
13.
【分析】利用 计算即可.
11【详解】
因为正方体ABCD-A B C D 的棱长为2,M、N分别为BB 、AB的中点
1 1 1 1 1
所以
故答案为:
考点 02 空间几何体三视图
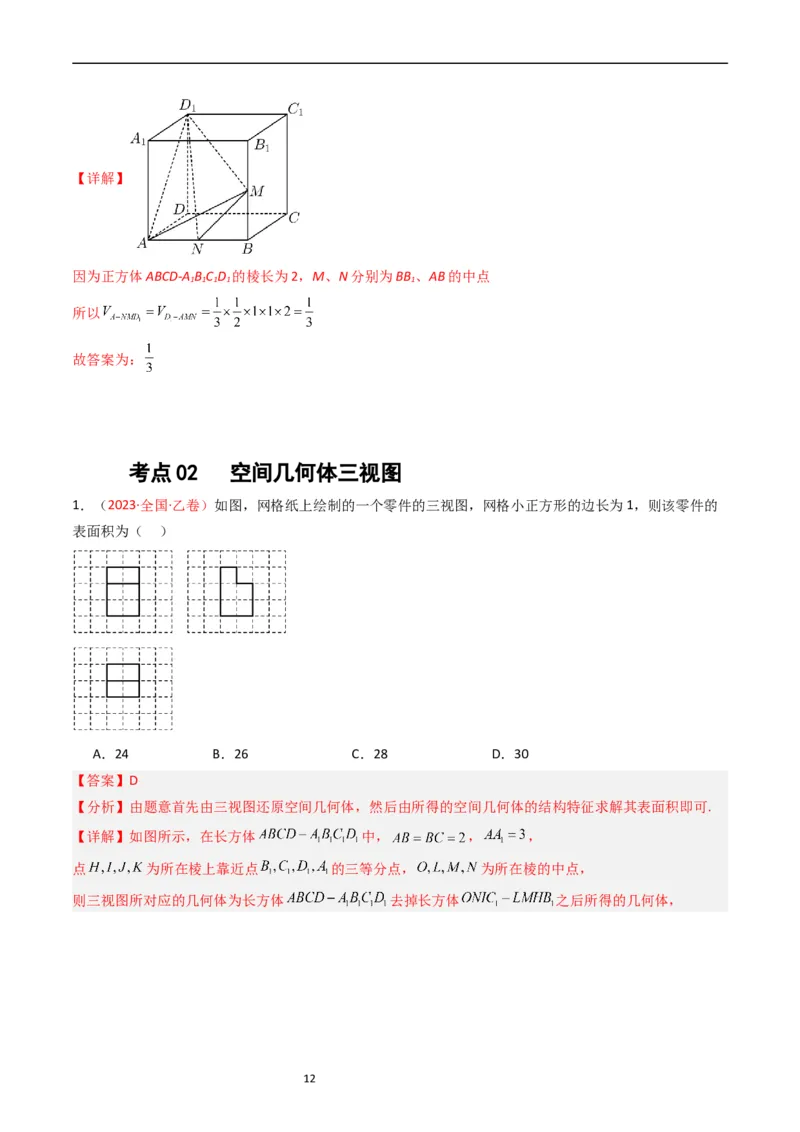
1.(2023·全国·乙卷)如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的
表面积为( )
A.24 B.26 C.28 D.30
【答案】D
【分析】由题意首先由三视图还原空间几何体,然后由所得的空间几何体的结构特征求解其表面积即可.
【详解】如图所示,在长方体 中, , ,
点 为所在棱上靠近点 的三等分点, 为所在棱的中点,
则三视图所对应的几何体为长方体 去掉长方体 之后所得的几何体,
12该几何体的表面积和原来的长方体的表面积相比少2个边长为1的正方形,
其表面积为: .
故选:D.
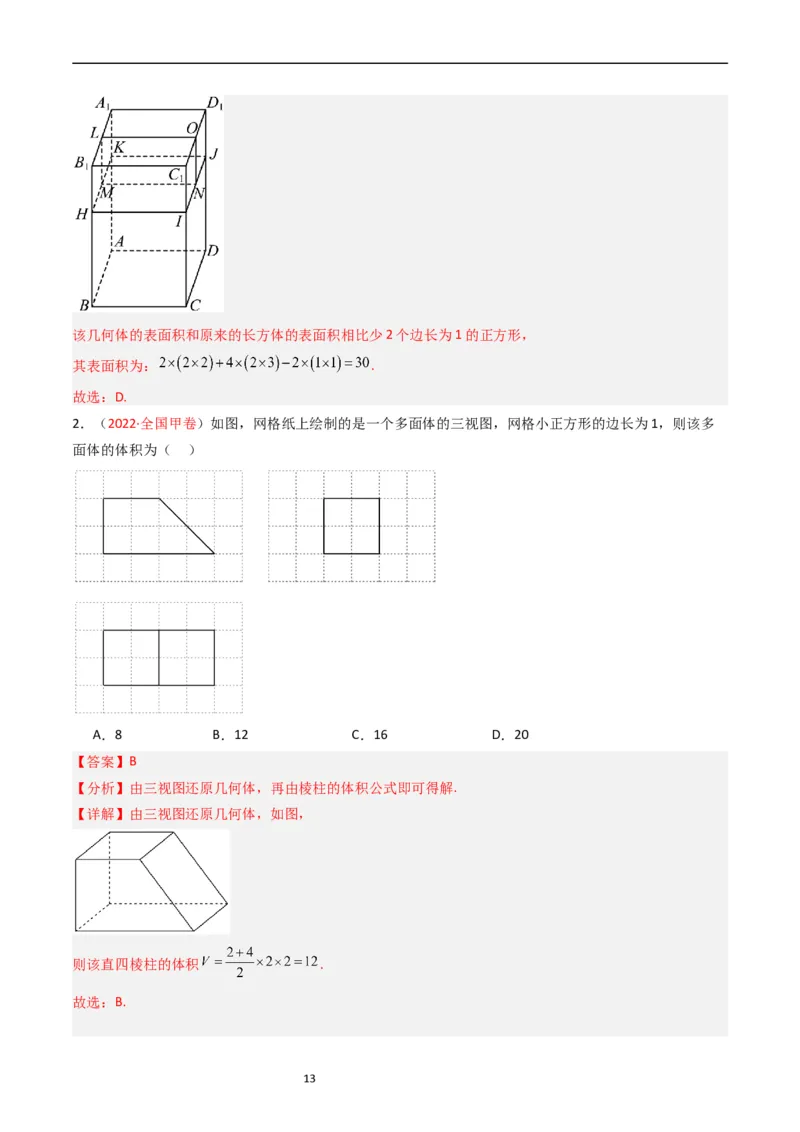
2.(2022·全国甲卷)如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多
面体的体积为( )
A.8 B.12 C.16 D.20
【答案】B
【分析】由三视图还原几何体,再由棱柱的体积公式即可得解.
【详解】由三视图还原几何体,如图,
则该直四棱柱的体积 .
故选:B.
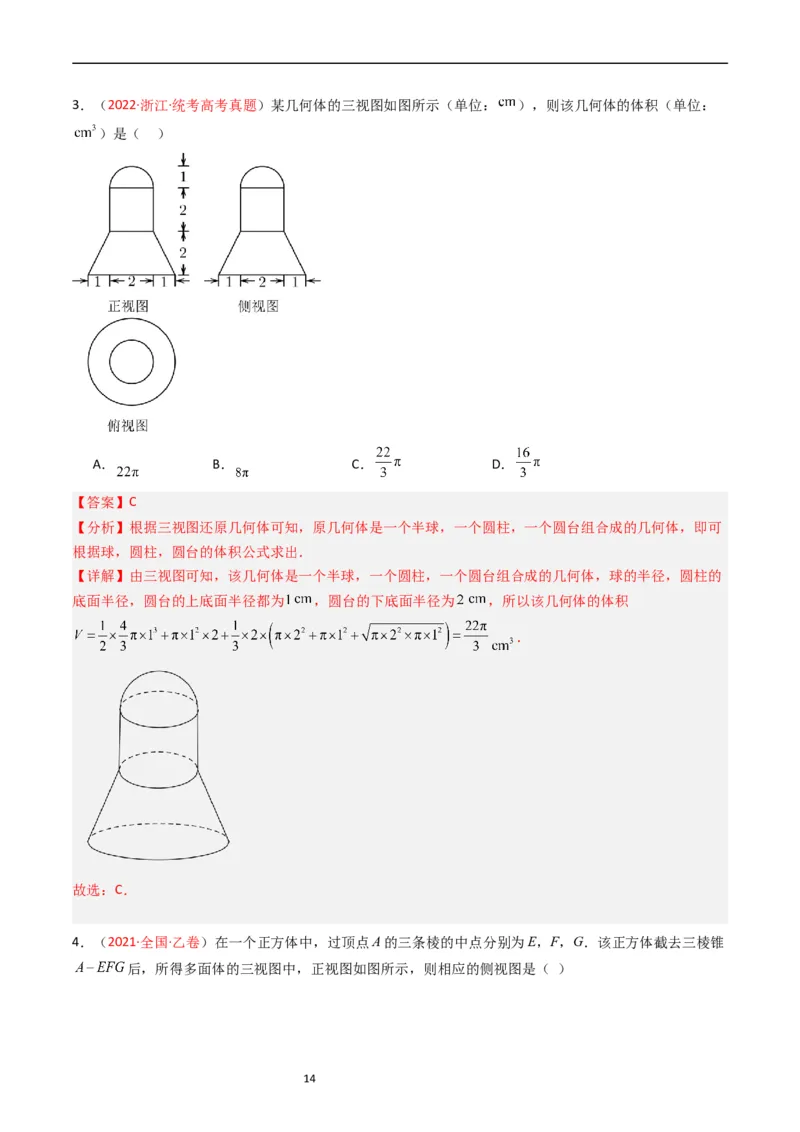
133.(2022·浙江·统考高考真题)某几何体的三视图如图所示(单位: ),则该几何体的体积(单位:
)是( )
A. B. C. D.
【答案】C
【分析】根据三视图还原几何体可知,原几何体是一个半球,一个圆柱,一个圆台组合成的几何体,即可
根据球,圆柱,圆台的体积公式求出.
【详解】由三视图可知,该几何体是一个半球,一个圆柱,一个圆台组合成的几何体,球的半径,圆柱的
底面半径,圆台的上底面半径都为 ,圆台的下底面半径为 ,所以该几何体的体积
.
故选:C.
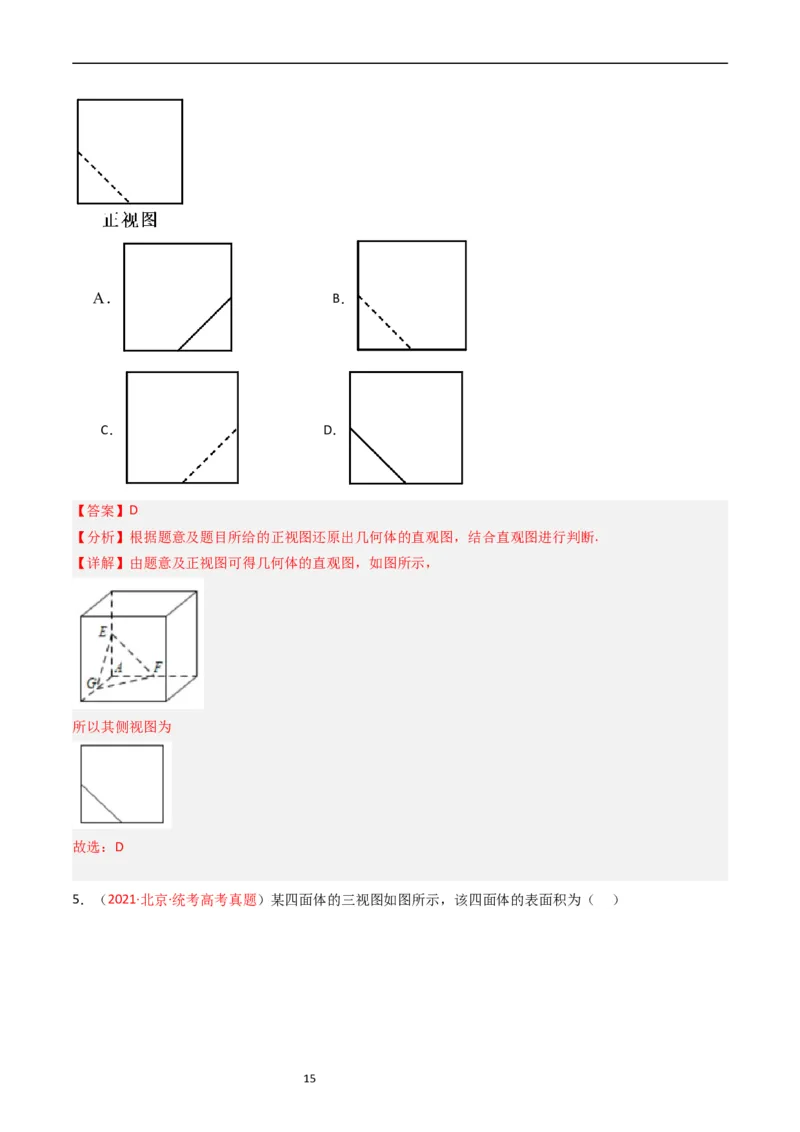
4.(2021·全国·乙卷)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥
后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )
14A. B.
C. D.
【答案】D
【分析】根据题意及题目所给的正视图还原出几何体的直观图,结合直观图进行判断.
【详解】由题意及正视图可得几何体的直观图,如图所示,
所以其侧视图为
故选:D
5.(2021·北京·统考高考真题)某四面体的三视图如图所示,该四面体的表面积为( )
15A. B. C. D.
【答案】A
【分析】根据三视图可得如图所示的几何体(三棱锥),根据三视图中的数据可计算该几何体的表面积.
【详解】根据三视图可得如图所示的几何体-正三棱锥 ,
其侧面为等腰直角三角形,底面等边三角形,
由三视图可得该正三棱锥的侧棱长为1,
故其表面积为 ,
故选:A.
6.(2021·浙江·统考高考真题)某几何体的三视图如图所示,则该几何体的体积是( )
16A. B.3 C. D.
【答案】A
【分析】根据三视图可得如图所示的几何体,根据棱柱的体积公式可求其体积.
【详解】几何体为如图所示的四棱柱 ,其高为1,底面为等腰梯形 ,
该等腰梯形的上底为 ,下底为 ,腰长为1,故梯形的高为 ,
故 ,
故选:A.
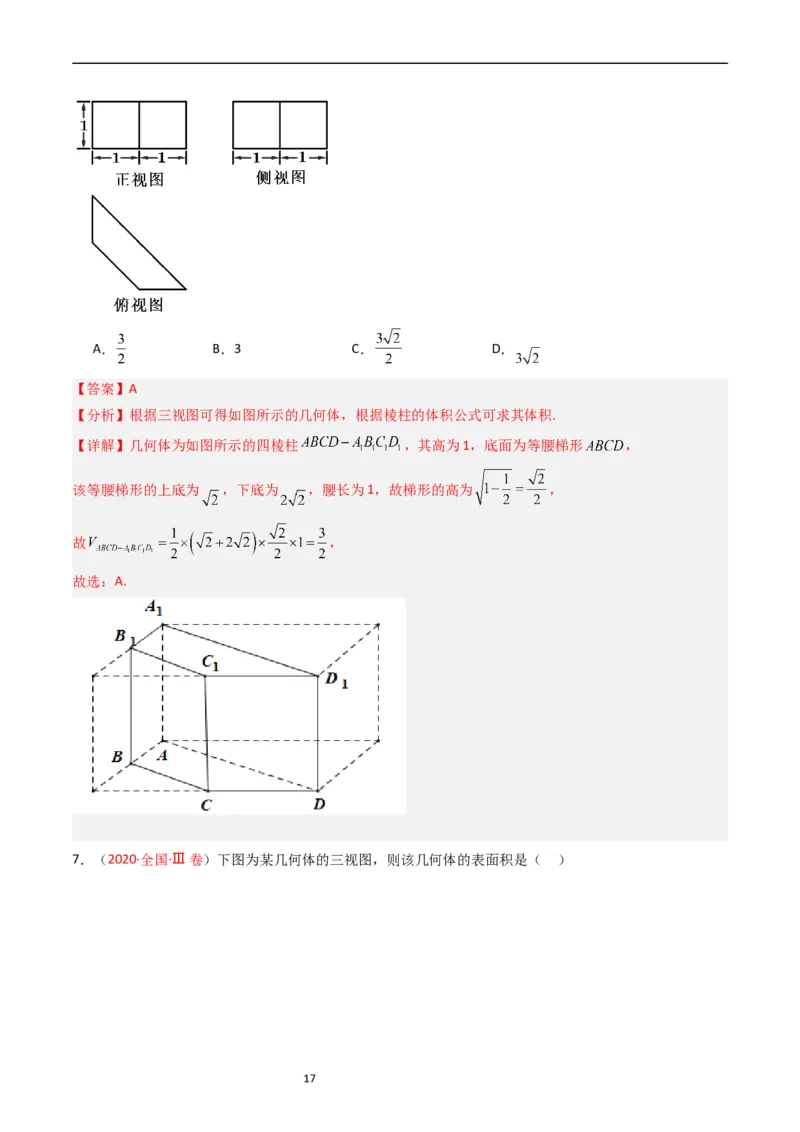
7.(2020·全国·Ⅲ卷)下图为某几何体的三视图,则该几何体的表面积是( )
17A.6+4 B.4+4 C.6+2 D.4+2
【答案】C
【分析】根据三视图特征,在正方体中截取出符合题意的立体图形,求出每个面的面积,即可求得其表面
积.
【详解】根据三视图特征,在正方体中截取出符合题意的立体图形
根据立体图形可得:
根据勾股定理可得:
是边长为 的等边三角形
根据三角形面积公式可得:
该几何体的表面积是: .
故选:C.
【点睛】本题主要考查了根据三视图求立体图形的表面积问题,解题关键是掌握根据三视图画出立体图形,
考查了分析能力和空间想象能力,属于基础题.
8.(2020·北京·统考高考真题)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为(
).
18A. B. C. D.
【答案】D
【分析】首先确定几何体的结构特征,然后求解其表面积即可.
【详解】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,
则其表面积为: .
故选:D.
【点睛】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图
中发现几何体中各元素间的位置关系及数量关系.
(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.
(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积
与底面圆的面积之和.
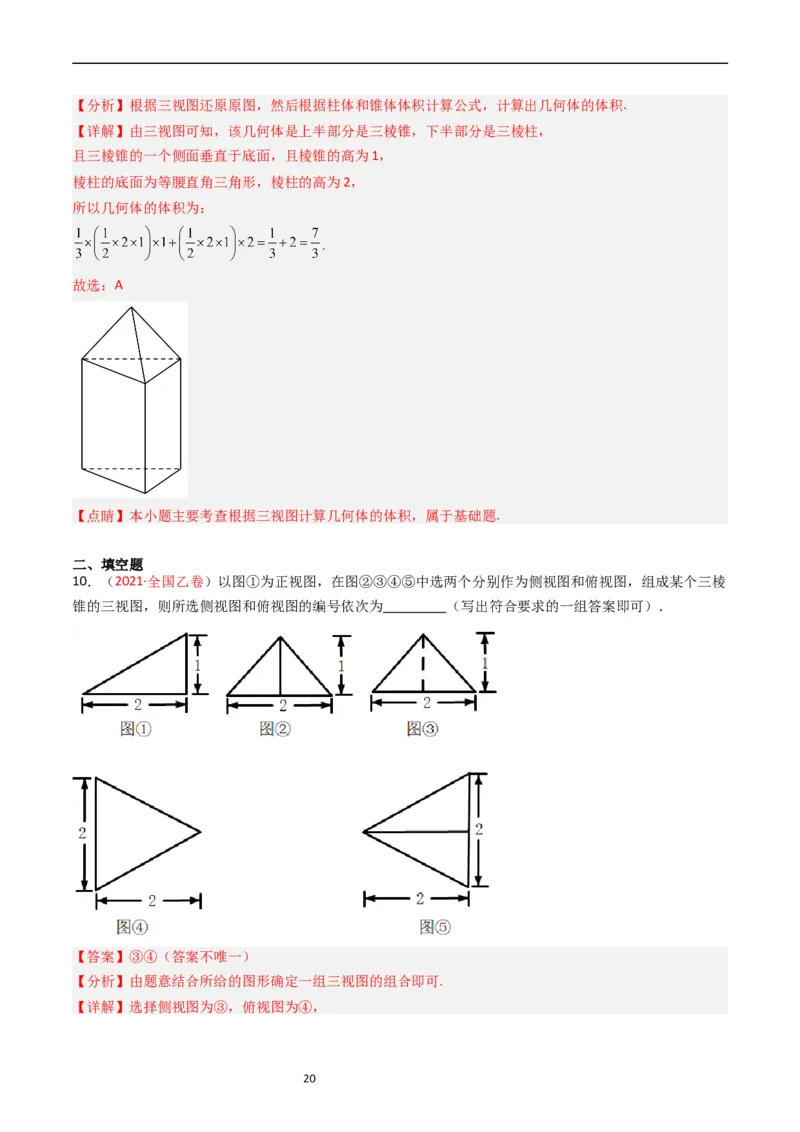
9.(2020·浙江·统考高考真题)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:
cm3)是( )
A. B. C.3 D.6
【答案】A
19【分析】根据三视图还原原图,然后根据柱体和锥体体积计算公式,计算出几何体的体积.
【详解】由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,
且三棱锥的一个侧面垂直于底面,且棱锥的高为1,
棱柱的底面为等腰直角三角形,棱柱的高为2,
所以几何体的体积为:
.
故选:A
【点睛】本小题主要考查根据三视图计算几何体的体积,属于基础题.
二、填空题
10.(2021·全国乙卷)以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱
锥的三视图,则所选侧视图和俯视图的编号依次为 (写出符合要求的一组答案即可).
【答案】③④(答案不唯一)
【分析】由题意结合所给的图形确定一组三视图的组合即可.
【详解】选择侧视图为③,俯视图为④,
20如图所示,长方体 中, ,
分别为棱 的中点,
则正视图①,侧视图③,俯视图④对应的几何体为三棱锥 .
故答案为:③④.
【点睛】三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关
系.
11.(2019·北京·高考真题)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网
格纸上小正方形的边长为1,那么该几何体的体积为 .
【答案】40.
【分析】本题首先根据三视图,还原得到几何体,根据题目给定的数据,计算几何体的体积.属于中等题.
21【详解】如图所示,在棱长为4的正方体中,三视图对应的几何体为正方体去掉棱柱 之后余
下的几何体,
几何体的体积 .
【点睛】(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直
观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得
出,则常用等积法、分割法、补形法等方法进行求解
属于中等题.
【详解】如图所示,在棱长为4的正方体中,三视图对应的几何体为正方体去掉棱柱 之后余
下的几何体,
几何体的体积 .
【点睛】(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直
观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得
出,则常用等积法、分割法、补形法等方法进行求解
22考点 03 空间几何体内接球外切球问题
1.(2022·全国·乙卷)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则
当该四棱锥的体积最大时,其高为( )
A. B. C. D.
【答案】C
【分析】方法一:先证明当四棱锥的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为
,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积
最大时其高的值.
【详解】[方法一]:【最优解】基本不等式
设该四棱锥底面为四边形ABCD,四边形ABCD所在小圆半径为r,
设四边形ABCD对角线夹角为 ,
则
(当且仅当四边形ABCD为正方形时等号成立)
即当四棱锥的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为
又设四棱锥的高为 ,则 ,
当且仅当 即 时等号成立.
故选:C
[方法二]:统一变量+基本不等式
由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为 ,底面所在圆的半径为 ,则 ,
所以该四棱锥的高 ,
(当且仅当 ,即 时,等号成立)
所以该四棱锥的体积最大时,其高 .
23故选:C.
[方法三]:利用导数求最值
由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为 ,底面所在圆的半径为 ,则 ,
所以该四棱锥的高 , ,令 , ,设 ,则
,
, ,单调递增, , ,单调递减,
所以当 时, 最大,此时 .
故选:C.
【点评】方法一:思维严谨,利用基本不等式求最值,模型熟悉,是该题的最优解;
方法二:消元,实现变量统一,再利用基本不等式求最值;
方法三:消元,实现变量统一,利用导数求最值,是最值问题的常用解法,操作简便,是通性通法.
2.(2022·全国·统考高考真题)已知正三棱台的高为1,上、下底面边长分别为 和 ,其顶点都在
同一球面上,则该球的表面积为( )
A. B. C. D.
【答案】A
【分析】根据题意可求出正三棱台上下底面所在圆面的半径 ,再根据球心距,圆面半径,以及球的半
径之间的关系,即可解出球的半径,从而得出球的表面积.
【详解】设正三棱台上下底面所在圆面的半径 ,所以 ,即 ,设球
心到上下底面的距离分别为 ,球的半径为 ,所以 , ,故 或
,即 或 ,解得 符合题意,所以球的表面积为
.
故选:A.
243.(2020·全国Ⅰ卷)已知 为球 的球面上的三个点,⊙ 为 的外接圆,若⊙ 的面积为
, ,则球 的表面积为( )
A. B. C. D.
【答案】A
【分析】由已知可得等边 的外接圆半径,进而求出其边长,得出 的值,根据球的截面性质,求
出球的半径,即可得出结论.
【详解】设圆 半径为 ,球的半径为 ,依题意,
得 , 为等边三角形,
由正弦定理可得 ,
,根据球的截面性质 平面 ,
,
球 的表面积 .
故选:A
【点睛】本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.
4.(2020·全国·Ⅱ卷)已知△ABC是面积为 的等边三角形,且其顶点都在球O的球面上.若球O的表面
积为16π,则O到平面ABC的距离为( )
25A. B. C.1 D.
【答案】C
【分析】根据球 的表面积和 的面积可求得球 的半径 和 外接圆半径 ,由球的性质可知所
求距离 .
【详解】
设球 的半径为 ,则 ,解得: .
设 外接圆半径为 ,边长为 ,
是面积为 的等边三角形,
,解得: , ,
球心 到平面 的距离 .
故选:C.
【点睛】本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明
确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.
二、填空题
5.(2023·全国乙卷)已知点 均在半径为2的球面上, 是边长为3的等边三角形, 平
面 ,则 .
【答案】2
【分析】先用正弦定理求底面外接圆半径,再结合直棱柱的外接球以及求的性质运算求解.
【详解】如图,将三棱锥 转化为直三棱柱 ,
设 的外接圆圆心为 ,半径为 ,
则 ,可得 ,
设三棱锥 的外接球球心为 ,连接 ,则 ,
因为 ,即 ,解得 .
故答案为:2.
26【点睛】方法点睛:多面体与球切、接问题的求解方法
(1)涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体的特殊点(一般为接、切点)或线作截面,
把空间问题转化为平面问题求解;
(2)若球面上四点P、A、B、C构成的三条线段PA、PB、PC两两垂直,且PA=a,PB=b,PC=c,一
般把有关元素“补形”成为一个球内接长方体,根据4R2=a2+b2+c2求解;
(3)正方体的内切球的直径为正方体的棱长;
(4)球和正方体的棱相切时,球的直径为正方体的面对角线长;
(5)利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的
位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.
6.(2019·全国Ⅱ卷)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正
方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或
两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,
它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有 个面,
其棱长为 .
【答案】 共26个面. 棱长为 .
【分析】第一问可按题目数出来,第二问需在正方体中简单还原出物体位置,利用对称性,平面几何解决.
【详解】由图可知第一层与第三层各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有
个面.
如图,设该半正多面体的棱长为 ,则 ,延长 与 交于点 ,延长 交正方体棱于 ,
由半正多面体对称性可知, 为等腰直角三角形,
27,
,即该半正多面体棱长为 .
【点睛】本题立意新颖,空间想象能力要求高,物体位置还原是关键,遇到新题别慌乱,题目其实很简单,
稳中求胜是关键.立体几何平面化,无论多难都不怕,强大空间想象能力,快速还原图形.
考点 04 空间几何题的综合应用
1.(2022·全国乙卷)已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则
当该四棱锥的体积最大时,其高为( )
A. B. C. D.
【答案】C
【分析】方法一:先证明当四棱锥的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为
,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积
最大时其高的值.
【详解】[方法一]:【最优解】基本不等式
设该四棱锥底面为四边形ABCD,四边形ABCD所在小圆半径为r,
设四边形ABCD对角线夹角为 ,
则
(当且仅当四边形ABCD为正方形时等号成立)
即当四棱锥的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为
又设四棱锥的高为 ,则 ,
28当且仅当 即 时等号成立.
故选:C
[方法二]:统一变量+基本不等式
由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为 ,底面所在圆的半径为 ,则 ,
所以该四棱锥的高 ,
(当且仅当 ,即 时,等号成立)
所以该四棱锥的体积最大时,其高 .
故选:C.
[方法三]:利用导数求最值
由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为 ,底面所在圆的半径为 ,则 ,
所以该四棱锥的高 , ,令 , ,设 ,则
,
, ,单调递增, , ,单调递减,
所以当 时, 最大,此时 .
故选:C.
【点评】方法一:思维严谨,利用基本不等式求最值,模型熟悉,是该题的最优解;
方法二:消元,实现变量统一,再利用基本不等式求最值;
方法三:消元,实现变量统一,利用导数求最值,是最值问题的常用解法,操作简便,是通性通法.
2.(2022·全国·新高考Ⅰ卷)已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为 ,
且 ,则该正四棱锥体积的取值范围是( )
29A. B. C. D.
【答案】C
【分析】设正四棱锥的高为 ,由球的截面性质列方程求出正四棱锥的底面边长与高的关系,由此确定正
四棱锥体积的取值范围.
【详解】∵球的体积为 ,所以球的半径 ,
[方法一]:导数法
设正四棱锥的底面边长为 ,高为 ,
则 , ,
所以 ,
所以正四棱锥的体积 ,
所以 ,
当 时, ,当 时, ,
所以当 时,正四棱锥的体积 取最大值,最大值为 ,
又 时, , 时, ,
所以正四棱锥的体积 的最小值为 ,
所以该正四棱锥体积的取值范围是 .
故选:C.
[方法二]:基本不等式法
由方法一故所以 当且仅当 取到 ,
30当 时,得 ,则
当 时,球心在正四棱锥高线上,此时 ,
,正四棱锥体积 ,故该正四棱锥体积的取值范围是
3.(2020·高考Ⅰ卷)已知 为球 的球面上的三个点,⊙ 为 的外接圆,若⊙ 的面积为
, ,则球 的表面积为( )
A. B. C. D.
【答案】A
【分析】由已知可得等边 的外接圆半径,进而求出其边长,得出 的值,根据球的截面性质,求
出球的半径,即可得出结论.
【详解】设圆 半径为 ,球的半径为 ,依题意,
得 , 为等边三角形,
由正弦定理可得 ,
,根据球的截面性质 平面 ,
,
球 的表面积 .
故选:A
【点睛】本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.
二、填空题
4.(2023·全国·统考高考乙卷)已知点 均在半径为2的球面上, 是边长为3的等边三角形,
平面 ,则 .
【答案】2
【分析】先用正弦定理求底面外接圆半径,再结合直棱柱的外接球以及求的性质运算求解.
31【详解】如图,将三棱锥 转化为直三棱柱 ,
设 的外接圆圆心为 ,半径为 ,
则 ,可得 ,
设三棱锥 的外接球球心为 ,连接 ,则 ,
因为 ,即 ,解得 .
故答案为:2.
【点睛】方法点睛:多面体与球切、接问题的求解方法
(1)涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体的特殊点(一般为接、切点)或线作截面,
把空间问题转化为平面问题求解;
(2)若球面上四点P、A、B、C构成的三条线段PA、PB、PC两两垂直,且PA=a,PB=b,PC=c,一
般把有关元素“补形”成为一个球内接长方体,根据4R2=a2+b2+c2求解;
(3)正方体的内切球的直径为正方体的棱长;
(4)球和正方体的棱相切时,球的直径为正方体的面对角线长;
(5)利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的
位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.
5.(2023·全国·统考高考甲卷)在正方体 中, 为 的中点,若该正方体的棱
与球 的球面有公共点,则球 的半径的取值范围是 .
【答案】
【分析】当球是正方体的外接球时半径最大,当边长为 的正方形是球的大圆的内接正方形时半径达到最
小.
【详解】设球的半径为 .
当球是正方体的外接球时,恰好经过正方体的每个顶点,所求的球的半径最大,若半径变得更大,球会包
含正方体,导致球面和棱没有交点,
32正方体的外接球直径 为体对角线长 ,即 ,故 ;
分别取侧棱 的中点 ,显然四边形 是边长为 的正方形,且 为正方形
的对角线交点,
连接 ,则 ,当球的一个大圆恰好是四边形 的外接圆,球的半径达到最小,即 的最
小值为 .
综上, .
故答案为:
6.(2020·山东·统考高考真题)已知直四棱柱ABCD–A B C D 的棱长均为2,∠BAD=60°.以 为球心,
1 1 1 1
为半径的球面与侧面BCC B 的交线长为 .
1 1
【答案】 .
【分析】根据已知条件易得 , 侧面 ,可得侧面 与球面的交线上的点到 的
距离为 ,可得侧面 与球面的交线是扇形 的弧 ,再根据弧长公式可求得结果.
【详解】如图:
取 的中点为 , 的中点为 , 的中点为 ,
因为 60°,直四棱柱 的棱长均为2,所以△ 为等边三角形,所以 ,
,
又四棱柱 为直四棱柱,所以 平面 ,所以 ,
因为 ,所以 侧面 ,
33设 为侧面 与球面的交线上的点,则 ,
因为球的半径为 , ,所以 ,
所以侧面 与球面的交线上的点到 的距离为 ,
因为 ,所以侧面 与球面的交线是扇形 的弧 ,
因为 ,所以 ,
所以根据弧长公式可得 .
故答案为: .
【点睛】本题考查了直棱柱的结构特征,考查了直线与平面垂直的判定,考查了立体几何中的轨迹问题,
考查了扇形中的弧长公式,属于中档题.
7.(2019·全国高考Ⅲ卷)学生到工厂劳动实践,利用 打印技术制作模型.如图,该模型为长方体
挖去四棱锥 后所得的几何体,其中 为长方体的中心, 分别为所在
棱的中点, , 打印所用原料密度为 ,不考虑打印损耗,制作该模型
所需原料的质量为 .
【答案】118.8
【分析】根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积,再求出模型的质
量.
【详解】由题意得, ,
四棱锥O−EFG的高3cm, ∴ .
又长方体 的体积为 ,
所以该模型体积为 ,
其质量为 .
34【点睛】本题考查几何体的体积问题,理解题中信息联系几何体的体积和质量关系,从而利用公式求解.
8.(2021 全国高考Ⅰ卷)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对
折,规格为 的长方形纸,对折1次共可以得到 , 两种规格的图形,它
们的面积之和 ,对折2次共可以得到 , , 三种规格的图形,
它们的面积之和 ,以此类推,则对折4次共可以得到不同规格图形的种数为 ;如果对折
次,那么 .
【答案】 5
【分析】(1)按对折列举即可;(2)根据规律可得 ,再根据错位相减法得结果.
【详解】(1)由对折2次共可以得到 , , 三种规格的图形,所以对着
三次的结果有: ,共4种不同规格(单位 ;
故对折4次可得到如下规格: , , , , ,共5种不同规格;
(2)由于每次对着后的图形的面积都减小为原来的一半,故各次对着后的图形,不论规格如何,其面积
成公比为 的等比数列,首项为120 ,第n次对折后的图形面积为 ,对于第n此对折后的
图形的规格形状种数,根据(1)的过程和结论,猜想为 种(证明从略),故得猜想 ,
设 ,
则 ,
两式作差得:
,
因此, .
35故答案为: ; .
【点睛】方法点睛:数列求和的常用方法:
(1)对于等差等比数列,利用公式法可直接求解;
(2)对于 结构,其中 是等差数列, 是等比数列,用错位相减法求和;
(3)对于 结构,利用分组求和法;
(4)对于 结构,其中 是等差数列,公差为 ,则 ,利用裂项相
消法求和.
36