文档内容
益阳市 2024 届高三 4 月教学质量检测
数学
(时量:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知 为虚数单位,若 ,则 ( )
A. B. C. D.
2.已知 ,则 是方程 的解的充要条件是( )
A. B.
C. D.
3.顶角为36°的等腰三角形,常称为“最美三角形”.已知 ,则“最美三角形”的底边长
与腰长的比为( )
A. B. C. D.
4.已知数列 满足 且 ,则 ( )
A.128 B.64 C.32 D.16
5.已知双曲线 与椭圆 有相同的焦点,则 的最小值为( )
A.6 B.7 C.8 D.9
6.2023年的某一天某红酒厂商为了在线出售其红酒产品,联合小Y哥直播间,邀请某“网红”来现场带货.
在带货期间,为吸引顾客光临直播间、增加客流量,发起了这样一个活动:如果在直播间进来的顾客中,出
现生日相同的顾客,则奖励生日相同的顾客红酒 1瓶.假设每个随机来访的顾客的出生日期都是相互独立的,
并且每个人都等可能地出生在一年(365天)中任何一天(2023年共365天),在 远小于365时,近似地
, ,其中 .如果要保证直播间至少两个人
学科网(北京)股份有限公司的生日在同一天的概率不小于 ,那么来到直播间的人数最少应该为( )
A.21 B.22 C.23 D.24
7.如图所示,4个球两两外切形成的几何体,称为一个“最密堆垒”.显然,即使是“最密堆垒”,4个球
之间依然存在着空隙.材料学研究发现,某种金属晶体中 4个原子的“最密堆垒”的空隙中如果再嵌入一个
另一种金属原子并和原来的4个原子均外切,则材料的性能会有显著性变化.记原金属晶体的原子半径为 ,
另一种金属晶体的原子半径为 ,则 和 的关系是( )
A. B. C. D.
8.已知 的定义域为 是 的导函数,且 , ,则
的大小关系是( )
A. B.
C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得6分,有选错的得0分,部分选对的得部分分.
9.下列命题中,正确的是( )
A.函数 与 表示同一函数
B.函数 与 是同一函数
C.函数 的图象与直线 的图象至多有一个交点
学科网(北京)股份有限公司D.函数 ,则 0
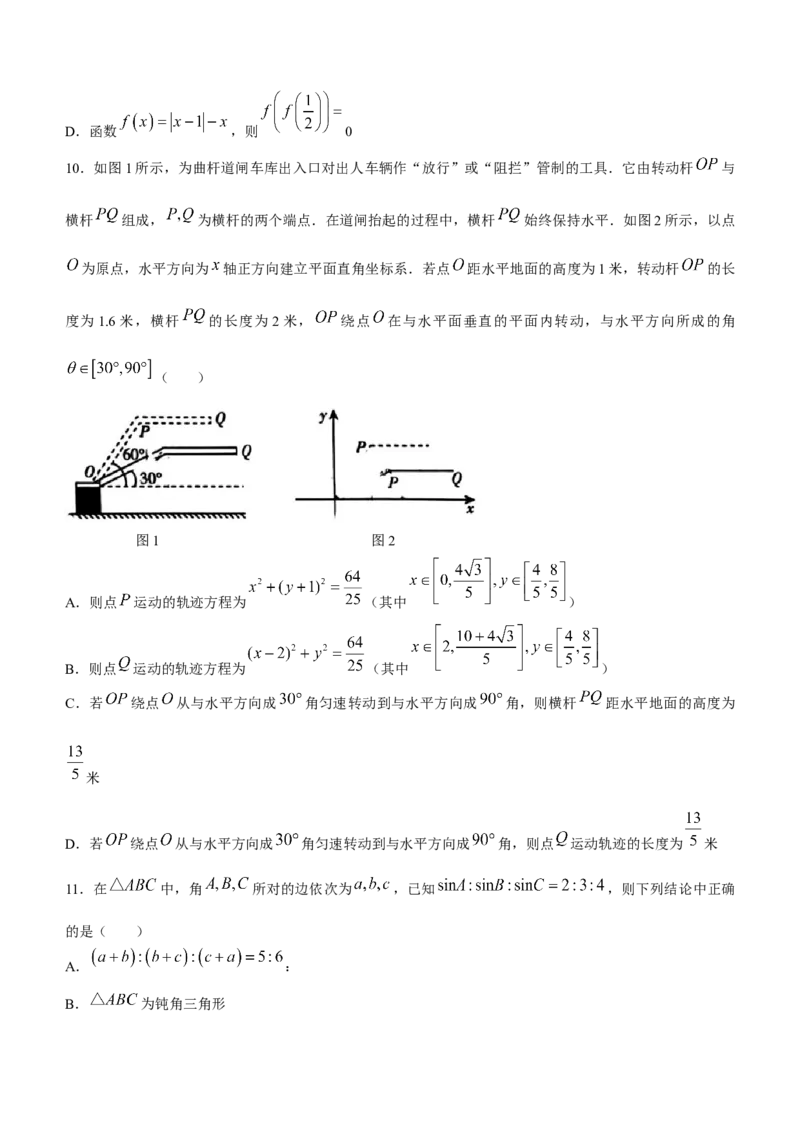
10.如图1所示,为曲杆道闸车库出入口对出人车辆作“放行”或“阻拦”管制的工具.它由转动杆 与
横杆 组成, 为横杆的两个端点.在道闸抬起的过程中,横杆 始终保持水平.如图2所示,以点
为原点,水平方向为 轴正方向建立平面直角坐标系.若点 距水平地面的高度为1米,转动杆 的长
度为1.6米,横杆 的长度为2米, 绕点 在与水平面垂直的平面内转动,与水平方向所成的角
( )
图1 图2
A.则点 运动的轨迹方程为 (其中 )
B.则点 运动的轨迹方程为 (其中 )
C.若 绕点 从与水平方向成 角匀速转动到与水平方向成 角,则横杆 距水平地面的高度为
米
D.若 绕点 从与水平方向成 角匀速转动到与水平方向成 角,则点 运动轨迹的长度为 米
11.在 中,角 所对的边依次为 ,已知 ,则下列结论中正确
的是( )
A. :
B. 为钝角三角形
学科网(北京)股份有限公司C.若 .则 的面积是
D.若 的外接圆半径是 ,内切圆半径为 ,则
三、填空题:本题共3小题,每小题5分,共15分.
12.在平面直角坐标系中,已知点 ,若 为平面上的一个动点且 ,则点
运动所形成的曲线的方程为______.
13 . 已 知 , 且 , 则 满 足
且 的 的最大值为______.
14 . 已 知 函 数 的 定 义 域 为 . 对 任 意 的 恒 有
, 且 . 则
______.
四、解答题:本题共5小题,共77分.请在答题卡指定区域内作答.解答时应写出文字说明、
证明过程或演算步骤.
15.(本小题满分13分)
已知 为正实数,构造函数 .若曲线 在点 处的切线方程为
.
(1)求 的值;
(2)求证: .
16.(本小题满分15分)
新鲜是水果品质的一个重要指标。某品牌水果销售店,为保障所销售的某种水果的新鲜度,当天所进的水果
如果当天没有销售完毕,则第二天打折销售直至售罄.水果销售店以每箱进货价50元、售价100元销售该种
水果,如果当天卖不完,则剩下的水果第二天将在原售价的基础上打五折特价销售,而且要整体支付包装更
换与特别处理等费用30元.这样才能保障第二天特价水果售罄,并且不影响正价水果销售,水果销售店经理
记录了在连续50天中该水果的日销售量x(单位:箱)和天数y(单位:天)如下表所示:
2
日销售量x(单位:箱) 22 23 24 26
5
学科网(北京)股份有限公司天数y(单位:天) 10 10 15 9 6
(1)为能减少打折销售份额,决定70%地满足顾客需求(即在100天中,大约有70天可以满足顾客需求).
请根据上面表格中的数据,确定每天此种水果的进货量t的值。(以箱为单位,结果保留一位小数)
(2)以这 50 天记录的日需求量的频率作为日需求量的概率,设( 1)中所求 的值满足
,请以期望作为决策依据,帮销售店经理判断每天购进此种水果是 箱划算还是
箱划算?
17.(本小题满分15分)
如图所示,四边形 为梯形, ,以 为一条边作矩形 ,
且 ,平面 平面 .
(1)求证: ;
(2)甲同学研究发现并证明了这样一个结论:如果两个平面所成的二面角为 ,其中一个平
面内的图形 在另一个平面上的正投影为 ,它们的面积分别记为 和 ,则 .乙同学
利用甲的这个结论,发现在线段 上存在点 ,使得 .请你对乙同学发现的结论进行证明.
18.(本小题满分17分)
已知直线 与椭圆 相交于点 ,点 在第一象限内, 分别为椭圆的左、
右焦点.
(1)设点 到直线 的距离分别为 ,求 的取值范围;
(2)已知椭圆 在点 处的切线为 .
学科网(北京)股份有限公司(1)求证:切线 的方程为 ;
(2)设射线 交 于点 ,求证: 为等腰三角形.
19.(本小题满分17分)
我们知道,二维空间(平面)向量可用二元有序数组 表示;三维空间向盘可用三元有序数组
表示.一般地, 维空间向量用 元有序数组 表示,其中 称为空
间向量的第 个分量, 为这个分量的下标.对于 维空间向量 ,定义集合
.记 的元素的个数为 (约定空集的元素个数为0).
(1)若空间向量 ,求 及 ;
(2)对于空间向量 .若 ,求证: ,若
,则 ;
(3)若空间向量 的坐标满足 ,当 时,求证:
.
学科网(北京)股份有限公司