文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷03(文科)
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.已知集合 ,则 ( )
A. B. C. D.
2.已知复数 满足 ,则 ( )
A. B. C.1 D.
3.设有n个样本 , ,…, ,其标准差是 ,另有n个样本 , ,…, ,且
,其标准差为 ,则下列关系中正确的是( )
A. B.
C. D.
4.已知 , , ,则a,b,c的大小关系是( )
A. B. C. D.
5.已知某品牌手机电池充满电量为 毫安,每经过 小时,电量消耗 ,若电池电量不超过 毫安
时充电最佳,那么该手机至少可以待机小时.(待机小时取整数,参考数据: , )
( )
A. B. C. D.
6.已知 ,则 =( )A. B. C. D.
7.( 2023·浙江宁波·统考一模)若 是夹角为 的两个单位向量, 与 垂直,则
( )
A. B. C. D.
8.求圆心在直线 上,且与直线 相切于点 的圆的方程是( )
A. B.
C. D.
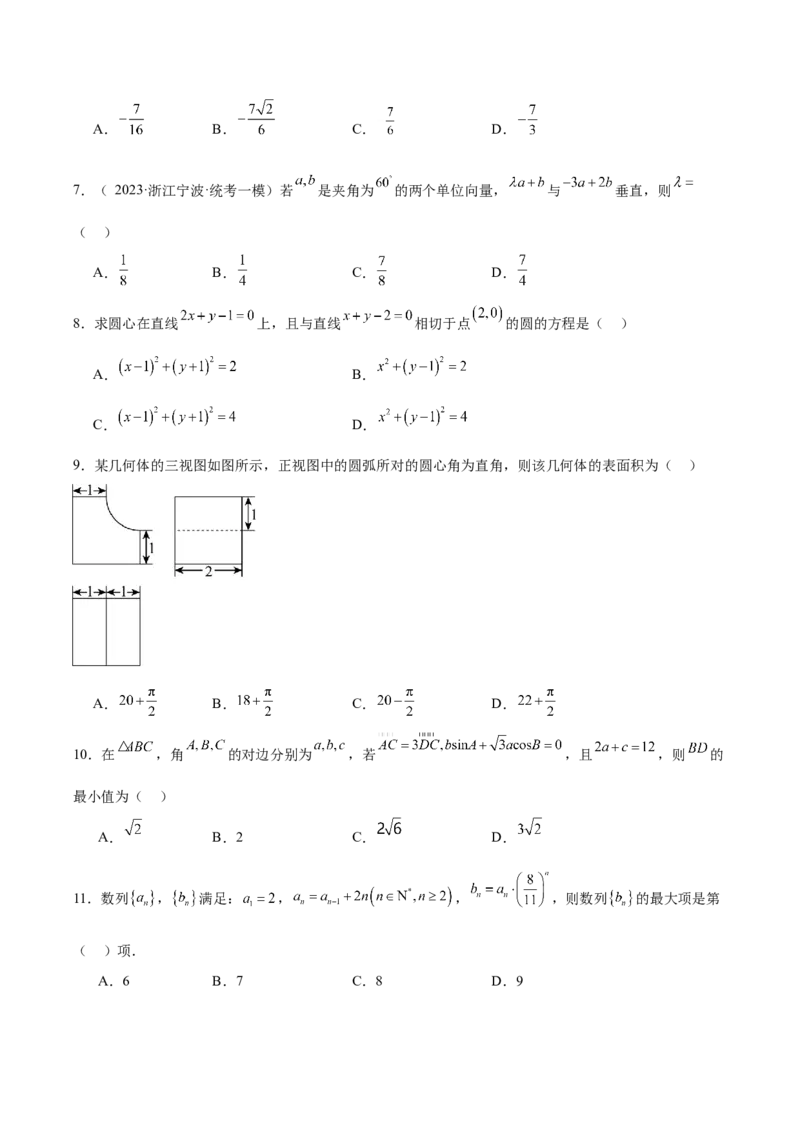
9.某几何体的三视图如图所示,正视图中的圆弧所对的圆心角为直角,则该几何体的表面积为( )
A. B. C. D.
10.在 ,角 的对边分别为 ,若 ,且 ,则 的
最小值为( )
A. B.2 C. D.
11.数列 , 满足: , , ,则数列 的最大项是第
( )项.
A.6 B.7 C.8 D.912.已知 在 上单调递减,则实数 的取值范围为( )
A. B.
C. D.
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.若实数x,y满足约束条件 ,则 的取值范围为 .
14.已知双曲线的渐近线方程为 ,且右顶点与椭圆 的右焦点重合,则这个双曲线的标准
方程是 .
15.已知函数 ,则 的最小值为 .
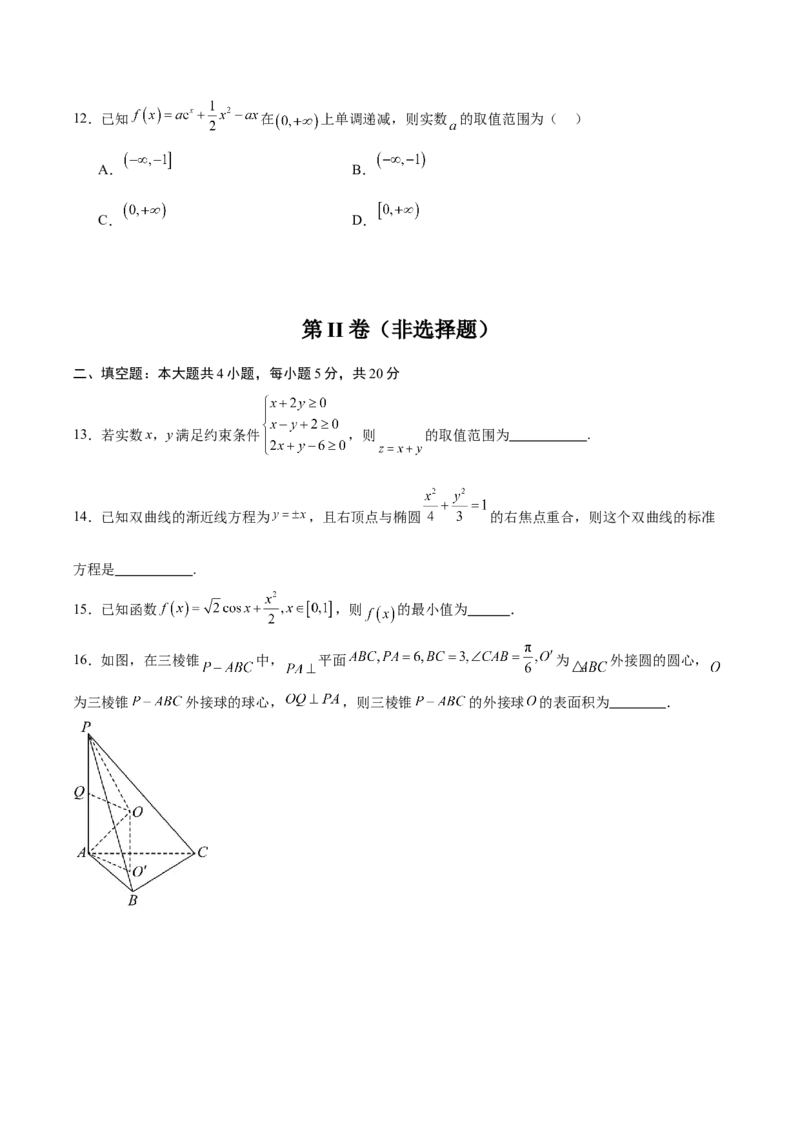
16.如图,在三棱锥 中, 平面 为 外接圆的圆心,
为三棱锥 外接球的球心, ,则三棱锥 的外接球 的表面积为 .三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)已知等比数列 的公比 ,若 ,且 分别是等差数列 的第
1,3,5项.
(1)求数列 和 的通项公式;
(2)记 ,求数列 的前 项和 .
18.(12分)2022年12月份以来,全国多个地区纷纷采取不同的形式发放多轮消费券,助力消费复苏.记
发放的消费券额度为x(百万元),带动的消费为y(百万元).某省随机抽查的一些城市的数据如下表所
示.
x 3 3 4 5 5 6 6 8
1
y 10 12 13 18 21 24 27
9
(1)根据表中的数据,请用相关系数说明y与x有很强的线性相关关系,并求出y关于x的线性回归方程.
(2)(ⅰ)若该省A城市在2023年2月份准备发放一轮额度为10百万元的消费券,利用(1)中求得的线性
回归方程,预计可以带动多少消费?
(ⅱ)当实际值与估计值的差的绝对值与估计值的比值不超过10%时,认为发放的该轮消费券助力消费复
苏是理想的.若该省A城市2月份发放额度为10百万元的消费券后,经过一个月的统计,发现实际带动的
消费为30百万元,请问发放的该轮消费券助力消费复苏是否理想?若不理想,请分析可能存在的原因.
参考公式: , , .当 时,两个变量之间具有很强的线性相关关系.
参考数据: .
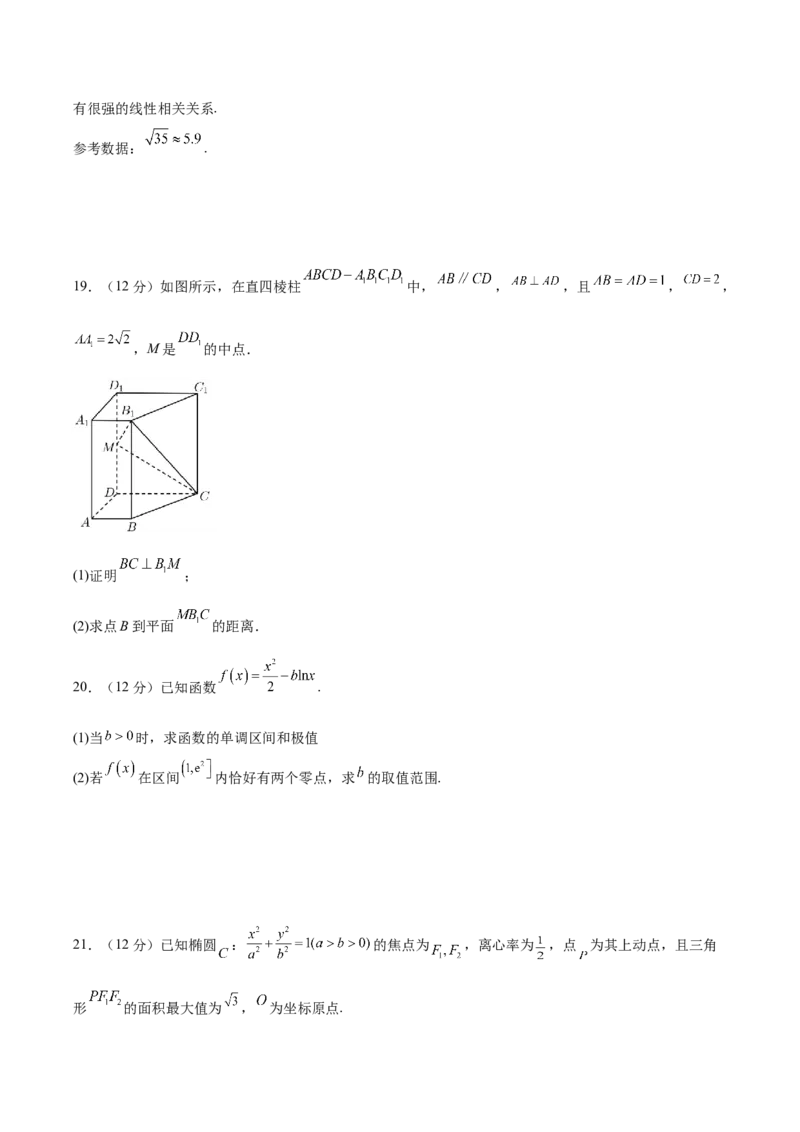
19.(12分)如图所示,在直四棱柱 中, , ,且 , ,
,M是 的中点.
(1)证明 ;
(2)求点B到平面 的距离.
20.(12分)已知函数 .
(1)当 时,求函数的单调区间和极值
(2)若 在区间 内恰好有两个零点,求 的取值范围.
21.(12分)已知椭圆 : 的焦点为 ,离心率为 ,点 为其上动点,且三角
形 的面积最大值为 , 为坐标原点.(1)求椭圆的 的方程;
(2)若点 为 上的两个动点,求常数 ,使 时,点 到直线 的距离为定值,求这
个定值.
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)已知曲线 的参数方程分别为 ( 为参数), ( 为参
数).
(1)将 的参数方程化为普通方程;
(2)以坐标原点 为极点,以 轴的非负半轴为极轴,建立极坐标系.若射线 与曲线 分别
交于 两点(异于极点),点 ,求 的面积.
选修4-5:不等式选讲
23.(10分)已知a、b均为正数,设 .
(1)当 时,求不等式 的解集;
(2)若 的最小值为6,求 的值,并求 的最小值.