2024届高中毕业班适应性练习卷数学参考答案及评分细则（定稿）_2024年3月_013月合集_2024届福建省三明市高三下学期3月质检_2024届福建3月省质检数学试题+答案

2024 届高中毕业班适应性练习卷 数学参考答案及评分细则 评分说明： 1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内 容比照评分标准制定相应的评分细则． 2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度， 可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答 有较严重的错误，就不再给分． 3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数．选择题和填空题不给中间分． 一、选择题：本大题考查基础知识和基本运算．每小题5分，满分40分． 1．B 2．D 3．A 4．C 5．A 6．C 7．B 8．B 二、选择题：本大题考查基础知识和基本运算．每小题 6 分，满分 18 分．全部选对的得 6 分，部分选对 的得部分分，有选错的得0分． 9．AD 10．ABD 11．BCD 三、填空题：本大题考查基础知识和基本运算．每小题5分，满分15分． 73 12．0.2718 13．56π；80π（仅答对一空给3分） 14． 5 四、解答题：本大题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 15.本小题主要考查正弦定理、余弦定理等基础知识，考查逻辑推理能力、运算求解能力等，考查化归与 转化思想、函数与方程思想、数形结合思想等，考查数学运算、逻辑推理等核心素养，体现基础性和 综合性．满分13分． 解法一：（1）由∠DAC+∠BAC =π，可得sin∠BAC =sin∠DAC . ··············································· 1分 AB BC 在△ABC中，由正弦定理，得 = ， ···························································· 3分 sinC sin∠BAC A BCsinC 所以AB= . sin∠BAC AD CD 在△ADC中，由正弦定理，得 = ， ··············· B ··················D·················C········· 5分 sinC sin∠DAC CDsinC 所以AD= . sin∠DAC AB BC 故 = . ············································································································· 6分 AD CD BC AB 因为D为BC的中点，所以 =2，即 =2. ································································ 7分 CD AD （2）由（1）不妨设AD=x，AB=2x，AC = y，BC =2 2y. ················································· 8分 ( 2y)2 + y2 −x2 在△ADC中，由余弦定理，得cosC = . ······················································ 9分 2× 2y×y (2 2y)2 + y2 −(2x)2 在△ABC中，由余弦定理，得cosC = . ················································ 10分 2×2 2y×y (2 2y)2 + y2 −(2x)2 ( 2y)2 + y2 −x2 所以 = . ···································································· 11分 2×2 2y×y 2× 2y×y 3 解得x2 = y2. ·········································································································· 12分 2 数学参考答案及评分细则 第1页（共 11页）3 3y2 − y2 3y2 −x2 2 3 2 故cosC = = = . ····································································· 13分 2 2y2 2 2y2 8 解法二：（1）由∠DAC+∠BAC =π，得sin∠BAC =sin∠DAC . ················································· 1分 BC S 因为D为BC的中点，所以 =2，所以 △ABC =2. ···················································· 3分 CD S △ADC 1 又因为S = AB⋅ACsin∠BAC， ········································································ 4分 △ABC 2 A 1 S = AD⋅ACsin∠DAC， ················································································· 5分 △ADC 2 1 AB⋅ACsin∠BAC B D C 2 所以 =2， ················································································ 6分 1 AD⋅ACsin∠DAC 2 AB 故 =2. ··········································································································· 7分 AD （2）由（1）不妨设AD=x，AB=2x，AC = y，BC =2 2y. ····································· 8分 x2 +( 2y)2 −(2x)2 在△ABD中，由余弦定理，得cos∠ADB= ， ···································· 9分 2×x× 2y x2 +( 2y)2 − y2 在△ACD中，由余弦定理，得cos∠ADC = ， ······································ 10分 2×x× 2y 因为∠ADB+∠ADC =π，所以cos∠ADB+cos∠ADC =0. x2 +( 2y)2 −(2x)2 x2 +( 2y)2 − y2 所以 + =0， ························································· 11分 2×x× 2y 2×x× 2y 3 解得x2 = y2. ···································································································· 12分 2 3 3y2 − y2 y2 +( 2y)2 −x2 2 3 2 故cosC = = = . ··························································· 13分 2×y× 2y 2 2y2 8 解法三：（1）设∠DAC =θ.由∠DAC+∠BAC =π，得∠BAC =π−θ，所以∠BAD=π−2θ. ··········· 1分 因为D为BC的中点，所以S =S ， ······························································· 2分 △ABD △ACD 1 1 所以 AB⋅ADsin(π−2θ)= AC⋅ADsinθ， ···················································A··········· 3分 2 2 即ABsin2θ= ACsinθ.因为sin2θ=2sinθcosθ，所以2ABcosθ= AC. ··················θ··········· 4分         因为2AD= AB+ AC，所以 4AD 2 = AB 2 + AC 2 +2AB⋅AC . ············································ 5分      B D C 即4|AD|2=|AB|2 +4|AB|2 cos2θ+4|AB|⋅(|AB|cosθ)cos(π−θ). ······································· 6分   AB 所以2|AD|=|AB|，即 =2. ················································································ 7分 AD （2）由（1）不妨设AD=x，AB=2x，AC = y，BC =2 2y.····································· 8分 y2 +x2 −( 2y)2 在△ADC中，由余弦定理，得cosθ= . ················································ 9分 2×y×x (2x)2 + y2 −(2 2y)2 在△ABC中，由余弦定理，得cos(π−θ)= . ···································· 10分 2×2x×y 数学参考答案及评分细则 第2页（共 11页）y2 +x2 −( 2y)2 (2x)2 + y2 −(2 2y)2 所以cosθ+cos(π−θ)= + =0. ································· 11分 2×y×x 2×2x×y 3 解得x2 = y2. ···································································································· 12分 2 3 3y2 − y2 y2 +( 2y)2 −x2 2 3 2 . 故cosC = = = ··························································· 13分 2×y× 2y 2 2y2 8 解法四：（1）取AB中点E，连结DE. ················································································ 1分 又D为BC中点，所以DE∥AC， ·································································A·········· 2分 所以∠BAC+∠DEA=π，∠DAC =∠EDA. ··························································G······· 4分 E 又∠DAC+∠BAC =π，所以∠DAC =∠DEA，故∠DEA=∠EDA， ································· 5分 所以AE= AD. ············································································ F ························· 6分 B D C AB 又AB=2AE，故 =2. ······················································································ 7分 AD （2）不妨设AC = y，BC =2 2y. 过A作AF ⊥DE于点F ，过D作DG⊥ AC于点G. ····················································· 8分 1 y 又DE∥AC，所以DE= AC= ，且AF ⊥ AC， ······················································· 9分 2 2 所以四边形AFDG为矩形. 1 y 因为AE= AD，所以DF = DE= . ······································································ 10分 2 4 y 3y 所以AG=DF = ，所以CG= . ········································································· 11分 4 4 1 又CD= BC= 2y， ··························································································· 12分 2 3y 所以cosC= CG = 4 = 3 2 . ················································································· 13分 CD 2y 8 16．本小题主要考查递推数列、等差数列、等比数列及数列求和等基础知识，考查运算求解能力、逻辑推 理能力等，考查化归与转化思想、分类与整合思想等，考查逻辑推理、数学运算等核心素养，体现基 础性、综合性．满分15分． 解法一：（1）因为a2 −a2 =8n，a =1，a >0， n+1 n 1 n 所以，当n=1时，a2 −a2 =8，a2 =a2 +8=9，所以a =3． ····························································· 1分 2 1 2 1 2 当n=2时，a2 −a2 =8×2，a2 =a2 +16=25，所以a =5． ··············································· 2分 3 2 3 2 3 当n2时，a2 =(a2 −a2 )+(a2 −a2 )++(a2 −a2)+a2 ·················································· 3分 n n n−1 n−1 n−2 2 1 1 =8(n−1)+8(n−2)++8×1+1 ························································································ 4分 =8[1+2++(n−1)]+1 n(n−1) =8× +1······················································································· 5分 2 =(2n−1)2， ··························································································· 6分 所以a =2n−1.·········································································································· 7分 n 当n=1时，a =1也符合上式． 1 综上，a =2n−1(n∈N*). ····························································································· 8分 n 数学参考答案及评分细则 第3页（共 11页）2n−1, n为奇数, 2n−1, n为奇数,   （2）由（1）得b n = 2n−1+1 即b n = n ··············································· 9分 2 4 ,n为偶数, 22, n为偶数. 记S =bb +bb +bb ++b b . 1 2 3 4 5 6 15 16 则S =1×21+5×22 +9×23 ++25×27 +29×28①， ·························································· 11分 2S = 1×22 +5×23 ++21×27 +25×28 +29×29②， ·············································· 12分 22×(1−27) ①−②，得−S = 1×21+4×22 +4×23 ++4×28 −29×29 =2+4× −29×29 =−12814， 1−2 ····························································································································· 14分 所以S = 12814， 故bb +bb +bb ++b b =12814. ············································································ 15分 1 2 3 4 5 6 15 16 解法二：（1）因为a2 −a2 =8n，a =1，a >0， n+1 n 1 n 所以，当n=1时，a2 −a2 =8，a2 =a2 +8=9，所以a =3． ····························································· 1分 2 1 2 1 2 当n=2时，a2 −a2 =8×2，a2 =a2 +16=25，所以a =5． ··············································· 2分 3 2 3 2 3 因为a2 −a2 =8n， n+1 n 所以a2 −a2 =(2n+1)2 −(2n−1)2，即a2 −(2n+1)2 =a2 −(2n−1)2． ···································· 5分 n+1 n n+1 n 所以a2 −(2n−1)2 =a2 −(2n−3)2 ==a2 −1=0，即a2 =(2n−1)2． ···································· 7分 n n−1 1 n 又a >0，所以a =2n−1(n∈N*). ················································································· 8分 n n 2n−1, n为奇数, 2n−1, n为奇数,   （2）由（1）得b n = 2n−1+1 即b n = n ··············································· 9分 2 4 ,n为偶数, 22, n为偶数. 记S =bb +bb +bb ++b b . 1 2 3 4 5 6 15 16 则S =1×21+5×22 +9×23 +13×24 +17×25 +21×26 +25×27 +29×28 ···································· 11分 =2+20+72+208+544+1344+3200+7424 ······························································ 14分 =12814. 故bb +bb +bb ++b b =12814. ············································································ 15分 1 2 3 4 5 6 15 16 17．本小题主要考查条件概率、全概率公式、概率的分布列及期望等基础知识，考查数学建模能力、运算 求解能力、逻辑推理能力等，考查统计与概率思想、分类与整合思想、函数与方程思想等，考查数学 抽象、数学建模和数学运算等核心素养，体现应用性和创新性．满分15分． 解法一：（1）依题意，X 的所有可能取值为0,1,2． ································································ 1分 设打成10:10后甲先发球为事件A，则乙先发球为事件 A ，且P(A)=P ( A ) = 1 ， 2 所以P(X =0)=P(A)⋅P ( X =0 A )+P ( A ) ⋅P ( X =0 A ) = 1 × 1 × 1 + 1 × 1 × 1 = 1 ， ···················· 2分 2 3 2 2 2 3 6 P(X =1)=P(A)⋅P ( X =1 A )+P ( A ) ⋅P ( X =1A ) = 1 ×   1 × 1 + 2 × 1 + 1 ×   1 × 1 + 1 × 2 = 1 ， ··· 3分 2 3 2 3 2 2 2 3 2 3 2 P(X =2)=P(A)⋅P ( X =2 A )+P ( A ) ⋅P ( X =2 A ) = 1 × 2 × 1 + 1 × 1 × 2 = 1 ． ························· 4分 2 3 2 2 2 3 3 所以X 的分布列为 X 0 1 2 1 1 1 P 6 2 3 1 1 1 7 故X 的均值为E(X)=0× +1× +2× = ． ································································· 5分 6 2 3 6 数学参考答案及评分细则 第4页（共 11页）（2）设第一局比赛甲获胜为事件B． 则P ( B X =0 )=0，P ( B X =1 )=P(B)，P ( B X= 2 )= 1． ················································· 7分 1 1 1 由（1）知，P(X =0)= ，P(X =1)= ，P(X =2)= ， 6 2 3 由全概率公式，得P(B)=P(X =0)P ( B X =0 )+P(X =1)P ( B X =1 )+P(X =2)P ( B X =2 ) 1 1 1 = ×0+ P(B)+ ， ····································································· 9分 6 2 3 2 2 解得P(B)= ，即第一局比赛甲获胜的概率 p = ． ····················································· 10分 3 0 3 2 2 （3）由（2）知 p = ，故估计甲每局获胜的概率均为 ， 0 3 3 设甲获胜时的比赛总局数为Y，因为每局的比赛结果相互独立， ········································· 12分 3 3 3 2 2 8 2 1 8 2 1 16 所以P(Y =3)=  = ，P(Y =4)=C1×  × = ，P(Y =5)=C2×  ×  = ． ·· 14分 3 27 3 3 3 27 4 3 3 81 64 故该场比赛甲获胜的概率P=P(Y =3)+P(Y =4)+P(Y =5)= ． ····································· 15分 81 解法二：（1）同解法一． ·································································································· 5分 （2）设第一局比赛甲获胜为事件B，10:10后的两球均为甲得分为事件B ，这两球甲和乙各得1分 1 为事件B ，易知B=B +BB ，事件B 与事件BB 互斥． 2 1 2 1 2 于是P(B)=P(B )+P(BB )=P(B )+P(B )P ( B B ) ． ····················································· 7分 1 2 1 2 2 当这两球甲和乙各得1分后比赛面临的形势与10:10时的形势一致，故P ( B B )=P(B)． 2 1 1 1 1 由（1）知P(B )=P(X =1)= ，P(B )=P(X =2)= ，所以P(B)= + P(B)， ················· 9分 2 2 1 3 3 2 2 2 解得P(B)= ，即第一局比赛甲获胜的概率 p = ． ······················································· 10分 3 0 3 2 2 （3）由（2）知 p = ，故估计甲每局获胜的概率均为 ，不妨设打满了5局且甲获胜局数为Y， 0 3 3  2 因为每局的比赛结果相互独立，所以Y B5, ． ························································· 12分  3 故该场比赛甲获胜的概率为P=P(Y =3)+P(Y =4)+P(Y =5) 3 2 4 5 2 1 2 1 2 =C3×  ×  +C4×  × +C5×  ·························· 14分 5 3 3 5 3 3 5 3 80 80 32 64 = + + = ． 243 243 243 81 64 所以该场比赛甲获胜的概率为 ．··············································································· 15分 81 解法三：（1）同解法一． ·································································································· 5分 1 1 （2）由（1）知P(X =1)= ，P(X =2)= ，由规则知打成10:10后必须再打2n球才能决出胜负． 2 3 设第一局比赛甲获胜为事件B，10:10后又打了2n球甲获胜为事件B ，依然平局为事件C ． 2n 2n 由于各球的比赛结果相互独立， 故P(C )=( P(X =1))n = 1 ，P(B )=P(X =2)⋅P(C )，P(B )=P(X =2)= 1 ． ·············· 8分 2n 2n 2n+2 2n 2 3 数学参考答案及评分细则 第5页（共 11页）n−1 1 1 所以P(B )= ⋅  ． ···························································································· 9分 2n 3 2 1 1  1−  n 3 2n  2 由于事件B 之间两两互斥，故P(B)= lim ∑P(B )= lim = ， 2n n→+∞ 2n n→+∞ 1 3 n=1 1− 2 2 即第一局比赛甲获胜的概率 p = ． ············································································ 10分 0 3 （3）同解法一． ······································································································· 15分 18．本小题主要考查平面与平面垂直的性质定理、直线与平面所成的角、解三角形、空间向量、椭圆的标 准方程及直线与椭圆的位置关系等基础知识，考查直观想象能力、逻辑推理能力、运算求解能力等， 考查数形结合思想、化归与转化思想、分类与整合思想等，考查直观想象、逻辑推理、数学运算等核 心素养，体现基础性、综合性与创新性．满分17分． 解法一：（1）因为平面ABC ⊥α，平面ABCα= AB，BC⊂平面ABC，BC ⊥ AB， 所以BC ⊥α． ·········································································································· 1分 所以直线CD在α内的射影为直线AB，所以直线CD与α所成角为∠CDB． ························· 2分 过D作DF ⊥ AC，垂足为F ．因为CD平分∠ACB，DB⊥BC ，所以DF =DB． 1 C 又AD=2DB，所以DF = AD，所以∠DAF =30°． ························································ 3分 2 F 又AB=6，∠ABC =90°，所以BC =2 3． 1 A D B 因为DB= AB=2，所以∠CDB=60°， E 3 α 所以直线CD与平面α所成角为60°． ············································································ 4分 （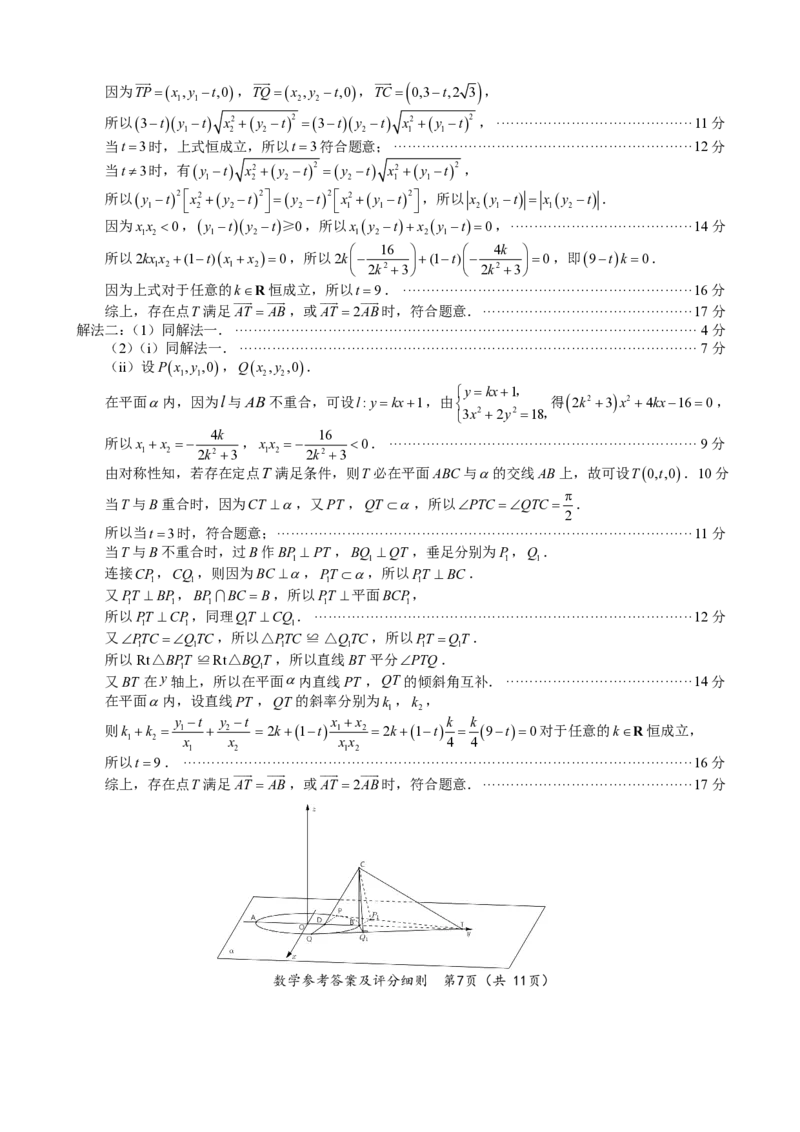2）（i）曲线Γ是椭圆． ································································· z ········· C ·················· 5分 理由如下： F 由（1）可知，DF ⊥ AC，DA=DC，所以F 是AC的中点． 设AB的中点为O，所以OF∥BC．又BC ⊥α，所以OF ⊥α． A O D B y G E 在α内过O作OG⊥ AB，所以OF ⊥OB，OF ⊥OG． α x    以O为原点，OG，OB，OF 所在的方向分别为x轴，y轴，z轴的正方向，建立空间直角坐标系 O−xyz，如图所示．因为OB=3，DB=2，所以OD=1．   设E(x,y,0)，又D(0,1,0)，C ( 0,3,2 3 ) ，则CE= ( x,y−3,−2 3 ) ，CD= ( 0,−2,−2 3 ) ．   CD⋅CE −2y+18 3 因为cos∠ECD=   ，又∠ECD=30°，所以 = ， ························ 6分 CD CE 4 x2 +(y−3)2 +12 2 x2 y2 化简得3x2 +2y2 =18，即 + =1，所以曲线Γ是椭圆． ················································ 7分 6 9 （ii）设P(x,y ,0)，Q(x ,y ,0)． 1 1 2 2 y=kx+1， 在平面α内，因为l与AB不重合，可设l:y=kx+1，由 得( 2k2 +3 ) x2 +4kx−16=0， 3x2 +2y2 =18， 4k 16 所以x +x =− ，xx =− <0． ·································································· 9分 1 2 2k2 +3 1 2 2k2 +3 由对称性知，若存在定点T 满足条件，则T必在平面ABC与α的交线AB上，故可设T(0,t,0)．10分     TP⋅TC TQ⋅TC 若∠PTC =∠QTC，则cos∠PTC =cos∠QTC，即   =   ． TP TC TQ TC 数学参考答案及评分细则 第6页（共 11页）   因为TP=(x,y −t,0)，TQ=(x ,y −t,0)，TC = ( 0,3−t,2 3 ) ， 1 1 2 2 所以(3−t)(y −t) x2 +(y −t)2 =(3−t)(y −t) x2 +(y −t)2 ， ·········································· 11分 1 2 2 2 1 1 当t =3时，上式恒成立，所以t =3符合题意； ································································ 12分 当t ≠3时，有(y −t) x2 +(y −t)2 =(y −t) x2 +(y −t)2 ， 1 2 2 2 1 1 所以(y −t)2x2 +(y −t)2=(y −t)2x2 +(y −t)2，所以 x (y −t) = x (y −t) ． 1  2 2  2  1 1  2 1 1 2 因为xx <0，(y −t)(y −t)≥0，所以x (y −t)+x (y −t)=0， ······································· 14分 1 2 1 2 1 2 2 1  16   4k  所以2kxx +(1−t)(x +x )=0，所以2k− +(1−t)− =0，即(9−t)k =0． 1 2 1 2  2k2 +3  2k2 +3 因为上式对于任意的k∈R恒成立，所以t =9． ······························································ 16分     综上，存在点T满足AT = AB，或AT =2AB时，符合题意． ············································· 17分 解法二：（1）同解法一． ··································································································· 4分 （2）（i）同解法一． ·································································································· 7分 （ii）设P(x,y ,0)，Q(x ,y ,0)． 1 1 2 2 y=kx+1， 在平面α内，因为l与AB不重合，可设l:y=kx+1，由 得( 2k2 +3 ) x2 +4kx−16=0， 3x2 +2y2 =18， 4k 16 所以x +x =− ，xx =− <0． ·································································· 9分 1 2 2k2 +3 1 2 2k2 +3 由对称性知，若存在定点T 满足条件，则T必在平面ABC与α的交线AB上，故可设T(0,t,0)．10分 π 当T与B重合时，因为CT ⊥α，又PT ，QT ⊂α，所以∠PTC =∠QTC = ． 2 所以当t =3时，符合题意； ························································································· 11分 当T与B不重合时，过B作BP ⊥PT ，BQ ⊥QT ，垂足分别为P，Q ． 1 1 1 1 连接CP，CQ ，则因为BC ⊥α，PT ⊂α，所以PT ⊥BC． 1 1 1 1 又PT ⊥BP，BP BC =B，所以PT ⊥平面BCP， 1 1 1 1 1 所以PT ⊥CP，同理QT ⊥CQ ． ················································································· 12分 1 1 1 1 又∠PTC =∠QTC，所以△PTC ≌△QTC，所以PT =QT． 1 1 1 1 1 1 所以Rt△BPT ≌Rt△BQT，所以直线BT 平分∠PTQ． 1 1 又BT 在y轴上，所以在平面α内直线PT ，QT 的倾斜角互补． ········································ 14分 在平面α内，设直线PT ，QT 的斜率分别为k ，k ， 1 2 y −t y −t x +x k k 则k +k = 1 + 2 =2k+(1−t) 1 2 =2k+(1−t) = (9−t)=0对于任意的k∈R恒成立， 1 2 x x xx 4 4 1 2 1 2 所以t =9． ············································································································· 16分     综上，存在点T满足AT = AB，或AT =2AB时，符合题意． ············································· 17分 数学参考答案及评分细则 第7页（共 11页）19．本小题主要考查集合、函数的零点、导数、数列和不等式等基础知识，考查逻辑推理能力、直观想 象能力、运算求解能力和创新能力等，考查函数与方程思想、化归与转化思想、分类与整合思想、 数形结合思想和特殊与一般思想等，考查数学抽象、逻辑推理、直观想象、数学运算等核心素养， 体现基础性、综合性与创新性．满分17分． 1 解法一：（1）当a=0时， f (x)= lnx+1，其定义域为(0,+∞)． 2 1 1 1−2x 由 f (x)=x得， lnx−x+1=0．设g(x)= lnx−x+1，则g'(x)= ． ·························· 1分 2 2 2x  1 1  当x∈0,  时，g'(x)＞0；当x∈ ,+∞ 时，g'(x)＜0；  2 2   1 1  所以g(x)在 0,  单调递增；在  ,+∞ 单调递减． ························································· 2分  2 2  1  1 注意到g(1)=0，所以g(x)在  ,+∞ 恰有一个零点x=1，且g  ＞g(1)=0， 2  2 又g ( e−2) =−e−2＜0，所以g ( e−2) g   1  ＜0，所以g(x)在  0, 1  恰有一个零点x ， 2  2 0 1   1 即 f (x)在  2 ,+∞  恰有一个不动点x=1，在   0, 2   恰有一个不动点x=x 0 ， ··························· 4分 所以A={x ,1}，所以A的元素个数为2．又因为x＜1，所以maxA=1． ······························ 5分 0 0 （2）（i）当a=0时，由（1）知，A有两个元素，不符合题意； ······································· 6分 1 1 当a＞0时，f (x)= lnx+ax2 +1−a，其定义域为(0,+∞)．由 f (x)=x得， lnx+ax2 −x+1−a=0． 2 2 1 1 4ax2 −2x+1 设h(x)= lnx+ax2 −x+1−a，则h'(x)= +2ax−1= ．·································· 7分 2 2x 2x 设F(x)=4ax2 −2x+1，则∆=4−16a． 1 ①当a≥ 时，∆≤0，F(x)≥0,h'(x)≥0，所以h(x)在(0,+∞)单调递增． 4 又h(1)=0，所以h(x)在(0,+∞)恰有一个零点x=1， 即 f (x)在(0,+∞)恰有一个不动点x=1，符合题意； ························································· 8分 1 ②当0＜a＜ ，∆＞0，故F(x)恰有两个零点x,x (x＜x )． 4 1 2 1 2 又因为F(0)=1＞0,F(1)=4a−1＜0，所以0＜x＜1＜x ． 1 2 当x∈(0,x )时，F(x)＞0,h'(x)＞0；当x∈(x,x )时，F(x)＜0,h'(x)＜0； 1 1 2 当x∈(x ,+∞)时，F(x)＞0,h'(x)＞0； 2 所以h(x)在(0,x )单调递增，在(x,x )单调递减，在(x ,+∞)单调递增； ······························ 9分 1 1 2 2 注意到h(1)=0，所以h(x)在(x,x )恰有一个零点x=1，且h(x )＞h(1)=0,h(x )＜h(1)=0， 1 2 1 2 又x→0时，h(x)→−∞，所以h(x)在(0,x )恰有一个零点x '， 1 0 从而 f (x)至少有两个不动点，不符合题意； 1  1  所以a的取值范围为  ,+∞ ，即集合B=  ,+∞ ． ························································ 10分 4  4  1  1 （ii）由（i）知，B=  ,+∞ ，所以a=minB= ， ······················································· 11分 4  4 数学参考答案及评分细则 第8页（共 11页）1 1 3 1 1 3 此时， f (x)= lnx+ x2 + ，h(x)= lnx+ x2 −x+ ，由（i）知，h(x)在(0,+∞)单调递增， 2 4 4 2 4 4 f (x) 所以，当x＞1时，h(x)＞h(1)=0，所以 f (x)＞x，即 ＞1， ········································ 12分 x 故若a >1，则a >1，因此，若存在正整数N使得a ≤1，则a ≤1，从而a ≤1， n n+1 N N−1 N−2 重复这一过程有限次后可得a≤1，与a =2矛盾，从而，∀n∈N*，a >1． ························· 13分 1 1 n 3 3 3 下面我们先证明当x＞1时，lnx＜ (x−1)．设G(x)=lnx− x+ ， 2 2 2 1 3 2−3x 则当x＞1时，G'(x)= − = <0，所以G(x)在(1,+∞)单调递减， x 2 2x 3 所以G(x)＜G(1)=0，即当x＞1时，lnx＜ (x−1)， 2 1 1 3 1 1 从而当x＞1时， lnx+ x2 + −x＜ x2 − x， 2 4 4 4 4 1 1 3 从而 2 lnx+ 4 x2 + 4 −1＜ 1 (x−1)，即 f (x) −1＜ 1 (x−1)， ················································ 15分 x 4 x 4 f (a ) 1 1 故 n −1＜ (a −1)，即a −1＜ (a −1)，由于a >1，a >1，所以a −1>0，a −1>0， a 4 n n+1 4 n n n+1 n n+1 n 1 1 1 1 1 故 a −1＜ a −1，故n≥2时， a −1＜ a −1＜ a −1＜＜ a −1 = ． ········ 16分 n+1 4 n n 4 n−1 42 n−2 4n−1 1 4n−1 1 1− 所以∀n∈N*，∑ n a −1≤∑ n 1 = 4n = 4   1− 1   ＜ 4 ，故maxC = 4 ． ··························· 17分 k 4k−1 1 3 4n  3 n 3 k=1 k=1 1− 4 解法二：（1）同解法一． ··································································································· 5分 1 （2）（i）当x=1时， lnx+ax2 +1−a=1=x，故x=1是 f (x)的一个不动点； ····················· 6分 2 1 lnx−x+1 当x≠1时，由 1 lnx+ax2 +1−a=x，得a= 2 （*）， 2 1−x2 1 要使得A恰有一个元素，即方程 lnx+ax2 +1−a=x有唯一解，因此方程（*）无实数解， 2 1 lnx−x+1 即直线y=a与曲线y= 2 无公共点． ································································ 7分 1−x2 1  1 1 3 lnx−x+1 x−x+lnx+ − +  令m(x)= 2 ，则m'(x)=  2x2 x 2 ．令n(x)=−x+lnx+ 1 − 1 + 3 (x＞0)， 1−x2 ( 1−x2)2 2x2 x 2 1 1 1 −x3 +x2 +x−1 −(x−1)2(x+1) 则n′(x)=−1+ − + = = ≤0， x x3 x2 x3 x3 所以n(x)在(0,+∞)单调递减，又因为n(1)=0，所以当x∈(0,1)时，n(x)>0，当x∈(1,+∞)时，n(x)<0， 所以当x∈(0,1)时，m′(x)>0，当x∈(1,+∞)时，m′(x)<0， 所以m(x)在(0,1)单调递增，在(1,+∞)单调递减， ····························································· 8分 数学参考答案及评分细则 第9页（共 11页）1 1 1 3 x−1− lnx lnx− + 令m (x)= 2 ，则m (1)=0，m '(x)= 2 2x 2 ， 1 x+1 1 1 (x+1)2 1 x−1− lnx 1 2 lnx−x+1 则limm(x)=lim 2 =lim x+1 =lim m 1 (x)−m 1 (1) =m ′ (1)= 1 ． x→1 x→1 1−x2 x→1 x−1 x→1 x−1 1 4 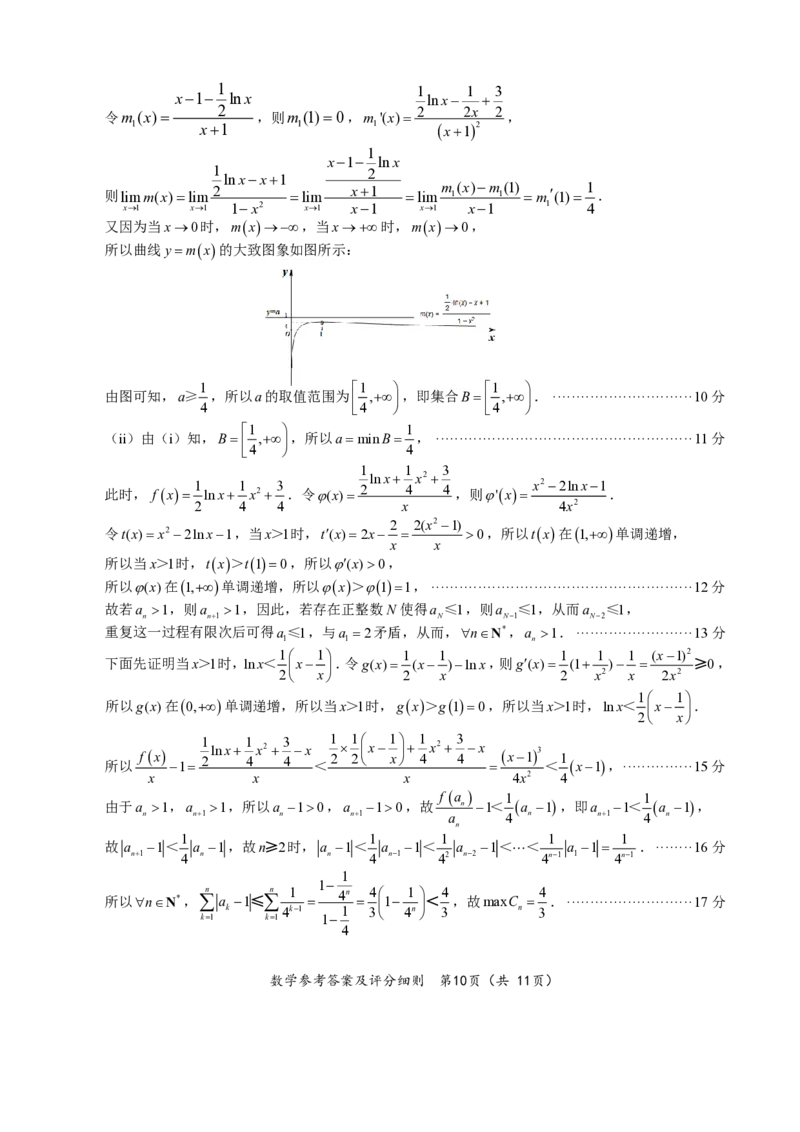又因为当x→0时，m(x)→−∞，当x→+∞时，m(x)→0， 所以曲线y=m(x)的大致图象如图所示： 1 1  1  由图可知，a≥ ，所以a的取值范围为  ,+∞ ，即集合B=  ,+∞ ． ······························ 10分 4 4  4  1  1 （ii）由（i）知，B=  ,+∞ ，所以a=minB= ， ······················································· 11分 4  4 1 1 3 lnx+ x2 + 此时， f (x)= 1 lnx+ 1 x2 + 3 ．令ϕ(x)= 2 4 4 ，则ϕ'(x)= x2 −2lnx−1 ． 2 4 4 x 4x2 2 2(x2 −1) 令t(x)=x2 −2lnx−1，当x＞1时，t′(x)=2x− = >0，所以t(x)在(1,+∞)单调递增， x x 所以当x＞1时，t(x)＞t(1)=0，所以ϕ′(x)>0， 所以ϕ(x)在(1,+∞)单调递增，所以ϕ(x)＞ϕ(1)=1， ························································ 12分 故若a >1，则a >1，因此，若存在正整数N使得a ≤1，则a ≤1，从而a ≤1， n n+1 N N−1 N−2 重复这一过程有限次后可得a≤1，与a =2矛盾，从而，∀n∈N*，a >1． ························· 13分 1 1 n 1 1 1 1 1 1 1 (x−1)2 下面先证明当x＞1时，lnx＜ x−  ．令g(x)= (x− )−lnx，则g′(x)= (1+ )− = ≥0， 2 x 2 x 2 x2 x 2x2 1 1 所以g(x)在(0,+∞)单调递增，所以当x＞1时，g(x)＞g(1)=0，所以当x＞1时，lnx＜ x−  ． 2 x 1 1 3 1 1 1 1 3 所以 f (x) −1= 2 lnx+ 4 x2 + 4 −x ＜ 2 × 2   x− x   + 4 x2 + 4 −x = (x−1)3 ＜ 1 (x−1)， ··············· 15分 x x x 4x2 4 f (a ) 1 1 由于a >1，a >1，所以a −1>0，a −1>0，故 n −1＜ (a −1)，即a −1＜ (a −1)， n n+1 n n+1 a 4 n n+1 4 n n 1 1 1 1 1 故 a −1＜ a −1，故n≥2时， a −1＜ a −1＜ a −1＜＜ a −1 = ． ········ 16分 n+1 4 n n 4 n−1 42 n−2 4n−1 1 4n−1 1 1− 所以∀n∈N*，∑ n a −1≤∑ n 1 = 4n = 4 1− 1   ＜ 4 ，故maxC = 4 ． ··························· 17分 k 4k−1 1 3 4n  3 n 3 k=1 k=1 1− 4 数学参考答案及评分细则 第10页（共 11页）解法三：（1）同解法一． ·································································································· 5分 （2）（i）同解法一． ································································································· 10分 （ii）同解法一得，∀n∈N*，a >1． ··········································································· 13分 n 1 1−x 下面我们先证明当x＞1时，lnx＜x−1．设G(x)=lnx−x+1，则当x＞1时，G'(x)= −1= <0， x x 所以G(x)在(1,+∞)单调递减，所以G(x)＜G(1)=0，即lnx＜x−1， 1 1 3 1 1 3 1 1 从而当x＞1时， lnx＜ (x−1)＜ (x−1)，于是 lnx+ x2 + −x＜ x2 − x， 2 2 4 2 4 4 4 4 1 1 3 从而 2 lnx+ 4 x2 + 4 −1＜ 1 (x−1)，即 f (x) −1＜ 1 (x−1)， ················································ 15分 x 4 x 4 f (a ) 1 1 故 n −1＜ (a −1)，即a −1＜ (a −1)，由于a >1，a >1，所以a −1>0，a −1>0， a 4 n n+1 4 n n n+1 n n+1 n 1 1 1 1 1 故 a −1＜ a −1，故n≥2时， a −1＜ a −1＜ a −1＜＜ a −1 = ． ········ 16分 n+1 4 n n 4 n−1 42 n−2 4n−1 1 4n−1 1 1− 所以∀n∈N*，∑ n a −1≤∑ n 1 = 4n = 4 1− 1   ＜ 4 ，故maxC = 4 ． ··························· 17分 k 4k−1 1 3 4n  3 n 3 k=1 k=1 1− 4 数学参考答案及评分细则 第11页（共 11页）