文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷03(文科)
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.已知集合 ,则 ( )
A. B. C. D.
【答案】C
【分析】化简集合A,B,根据集合的交集运算求解即可.
【详解】因为 ,
所以 ,
故选:C
2.已知复数 满足 ,则 ( )
A. B. C.1 D.
【答案】C
【分析】先求出 ,然后再求 .
【详解】由 ,得: ,
所以: ,即: ,故C项正确.
故选:C.
3.设有n个样本 , ,…, ,其标准差是 ,另有n个样本 , ,…, ,且
,其标准差为 ,则下列关系中正确的是( )
A. B.C. D.
【答案】B
【分析】根据标准差的计算公式分别表示 ,由此判断两者关系.
【详解】设样本 , ,…, 的平均数为 ,样本 , ,…, 的平均数为 ,则
,
,
,
,
所以 ,故 ,
故选:B.
4.已知 , , ,则a,b,c的大小关系是( )
A. B. C. D.
【答案】B
【分析】计算 , , ,得到大小关系.
【详解】 , , ,故 .
故选:B.
5.已知某品牌手机电池充满电量为 毫安,每经过 小时,电量消耗 ,若电池电量不超过 毫安
时充电最佳,那么该手机至少可以待机小时.(待机小时取整数,参考数据: , )
( )
A. B. C. D.
【答案】A
【分析】分析可知 小时后,该手机剩余的电量为 毫安,解不等式 可
得结论.【详解】由题意可知, 小时后,该手机剩余的电量为 毫安,
小时后,该手机剩余的电量为 毫安, ,
以此类推可知, 小时后,该手机剩余的电量为 毫安,
由 ,即 ,
所以, ,
因此,该手机至少可以待机 小时.
故选:A.
6.已知 ,则 =( )
A. B. C. D.
【答案】D
【分析】由倍角公式和差角公式、平方关系求解即可.
【详解】 .
故选:D
7.( 2023·浙江宁波·统考一模)若 是夹角为 的两个单位向量, 与 垂直,则
( )
A. B. C. D.
【答案】B【分析】由题意先分别算出 的值,然后将“ 与 垂直”等价转换为
,从而即可求解.
【详解】由题意有 ,
又因为 与 垂直,
所以 ,
整理得 ,解得 .
故选:B.
8.求圆心在直线 上,且与直线 相切于点 的圆的方程是( )
A. B.
C. D.
【答案】A
【分析】设出圆心坐标,根据圆心到直线 的距离等于圆心到 的距离求解出圆心坐标,从
而半径可求,则圆的方程可知.
【详解】因为圆心在直线 上,所以设圆心 ,
因为圆与直线 相切于点 ,
所以 ,解得 ,
所以圆心为 ,半径为 ,
所以圆的方程为 ,
故选:A.
9.某几何体的三视图如图所示,正视图中的圆弧所对的圆心角为直角,则该几何体的表面积为( )A. B. C. D.
【答案】A
【分析】根据三视图可还原几何体的直观图,从而可通过运算得出结论.
【详解】根据题意可知,
该几何体为一个正方体截掉四分之一圆柱(圆柱的上、下底面圆心的连线为正方体的一条棱,圆柱底面圆
的半径为正方体棱长的一半)所剩几何体,
所以该几何体的表面积为 ,
故选:A.
10.在 ,角 的对边分别为 ,若 ,且 ,则 的
最小值为( )
A. B.2 C. D.
【答案】B
【分析】已知 ,由正弦定理边化角,化简可得 ,设 ,在
和 中,由余弦定理可得 ,可求 的最小值.
【详解】由 及正弦定理可得 ,由 , 可得 ,故 .
通解 设 ,由 可得 ,
由余弦定理可得 ,又 ,
所以 ,得 .
在 和 中,由余弦定理得 , ,
由 可得 ,
故 ,
当 时, 取得最小值12,即 ,得 ,故 的最小值为2.
优解 由题意知 ,
两边同时平方得 ,
又 ,所以当且仅当 ,即 时取等号,
则 ,故 的最小值为2.
故选:B
11.数列 , 满足: , , ,则数列 的最大项是第
( )项.
A.6 B.7 C.8 D.9
【答案】A
【分析】根据累加法求出 , .设数列 的最大项是第 项,由得出不等式组,求解即可得出答案.
【详解】由已知可得,
,
,
,
,
两边分别相加可得,
,
所以有 .
因为 ,
所以, .
设数列 的最大项是第 项,
则有 ,即 ,
整理可得, ,解得 .
又 ,所以 .
故选:A.12.已知 在 上单调递减,则实数 的取值范围为( )
A. B.
C. D.
【答案】A
【分析】确定 在 上恒成立,根据 得到 ,再证明充分性,
,设 ,求导得到单调区间,计算最值得到证明.
【详解】 , 在 上恒成立,
设 , , ,
①必要性:
, 恒成立,故 ,
故 ,
若 ,则存在 ,使 时, , 单调递增,
,不满足条件;
②充分性:
, ,
设 , 在 恒成立,故 单调递减, ,故 恒成
立,
综上所述: .
故选:A.
【点睛】关键点睛:本题考查了利用导数解决函数单调性问题,意在考查学生的计算能力,转化能力和综
合应用能力,其中利用必要性探路得到 ,再证明充分性可以避免繁琐的讨论,简化运算,是解题的
关键.第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.若实数x,y满足约束条件 ,则 的取值范围为 .
【答案】
【分析】先作出平面区域,可知 表示斜率为 ,纵截距为 的直线 ,数形结合处理问题.
【详解】如图,作出约束条件的平面区域,
联立方程 ,解得 ,即点 ,
因为 ,即 ,表示斜率为 ,纵截距为 的直线 ,
可知:当直线 过点 时,目标函数 取到最小值 ,
所以 的取值范围为 .
故答案为: .
14.已知双曲线的渐近线方程为 ,且右顶点与椭圆 的右焦点重合,则这个双曲线的标准
方程是 .
【答案】【分析】根据渐近线可得 ,然后根据椭圆的焦点即可求出双曲线的顶点,即可求出结果.
【详解】设双曲线的方程是 ,
双曲线的渐近线方程是 , ①.
由椭圆 的方程知右焦点 ,则双曲线的右顶点坐标为
双曲线方程中的 ②.
解①②得: , , 所求双曲线的标准方程为 .
故答案为: .
15.已知函数 ,则 的最小值为 .
【答案】
【分析】根据题意,求得 ,设 ,求得 ,得到函数
的单调性,进而求得 在 上单调递减,进而求得 的最小值,得到答案.
【详解】因为 ,可得 ,
设 ,则 ,
令 ,可得 ,令 ,得 ,
所以函数 ,即函数 在 上单调递减,在 上单调递增,
又因为 , ,
所以 ,所以 在 上单调递减,则 .
故答案为: .16.如图,在三棱锥 中, 平面 为 外接圆的圆心,
为三棱锥 外接球的球心, ,则三棱锥 的外接球 的表面积为 .
【答案】
【分析】依题意由正弦定理可求得 外接圆的半径为 ,再利用线面垂直关系确定球心位置在
的正上方,由勾股定理可求出外接球的半径为 ,即可得出求的表面积.
【详解】根据题意可知,设 外接圆的半径为 ,
在 中由正弦定理可知 ,解得 ,即 ;
易知三棱锥 外接球的球心在 的正上方,且 平面 ;
又 平面 ,所以 ;
因为 平面 ,可得 ,又 ,
所以可得四边形 是矩形,即 ;
设 ,三棱锥 外接球的半径为 ,
由勾股定理可得 ,解得 ;
所以可得三棱锥 的外接球 的表面积为 .
故答案为:
【点睛】关键点点睛:本题突破口在于利用正弦定理将 外接圆的半径为 求出,并根据线面垂直关
系再确定其位置,由勾股定理求出外接球半径大小即可得球的表面积.
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.
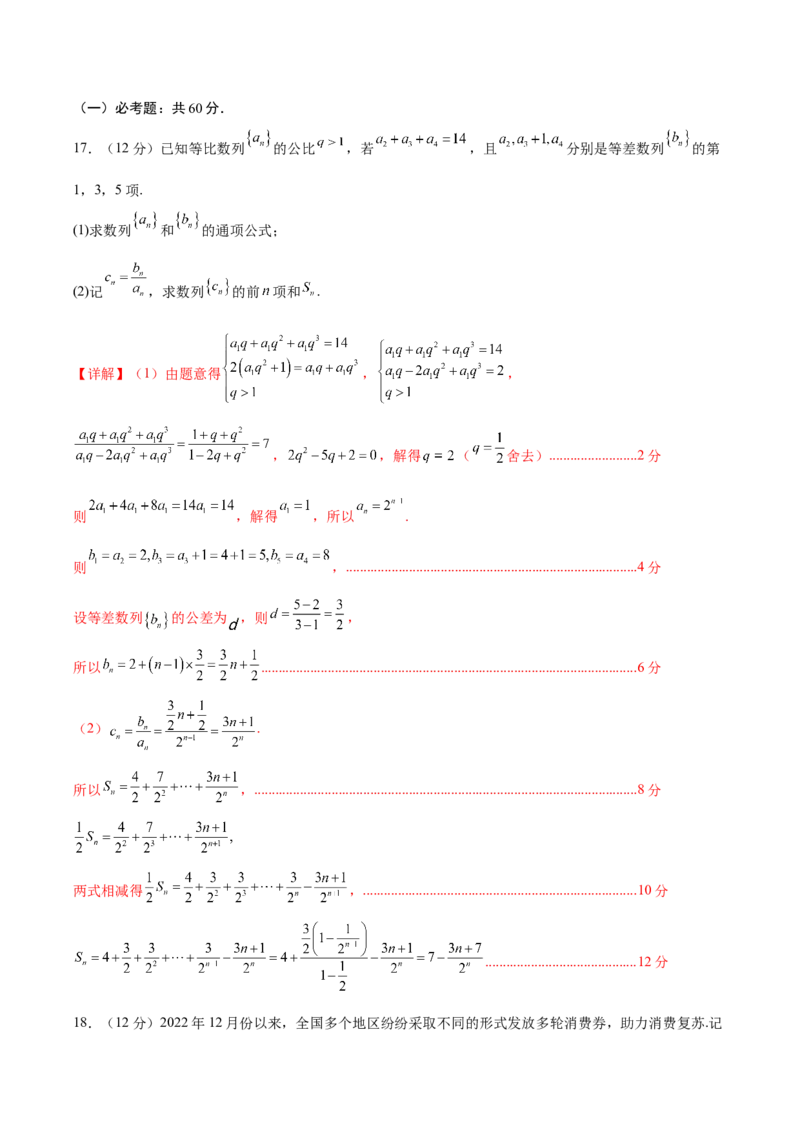
17.(12分)已知等比数列 的公比 ,若 ,且 分别是等差数列 的第
1,3,5项.
(1)求数列 和 的通项公式;
(2)记 ,求数列 的前 项和 .
【详解】(1)由题意得 , ,
, ,解得 ( 舍去).........................2分
则 ,解得 ,所以 .
则 ,...................................................................................4分
设等差数列 的公差为 ,则 ,
所以 ...........................................................................................................6分
(2) .
所以 ,.............................................................................................................8分
两式相减得 ,..............................................................................10分
...........................................12分
18.(12分)2022年12月份以来,全国多个地区纷纷采取不同的形式发放多轮消费券,助力消费复苏.记发放的消费券额度为x(百万元),带动的消费为y(百万元).某省随机抽查的一些城市的数据如下表所
示.
x 3 3 4 5 5 6 6 8
1
y 10 12 13 18 21 24 27
9
(1)根据表中的数据,请用相关系数说明y与x有很强的线性相关关系,并求出y关于x的线性回归方程.
(2)(ⅰ)若该省A城市在2023年2月份准备发放一轮额度为10百万元的消费券,利用(1)中求得的线性
回归方程,预计可以带动多少消费?
(ⅱ)当实际值与估计值的差的绝对值与估计值的比值不超过10%时,认为发放的该轮消费券助力消费复
苏是理想的.若该省A城市2月份发放额度为10百万元的消费券后,经过一个月的统计,发现实际带动的
消费为30百万元,请问发放的该轮消费券助力消费复苏是否理想?若不理想,请分析可能存在的原因.
参考公式: , , .当 时,两个变量之间具
有很强的线性相关关系.
参考数据: .
【详解】(1) ,
......................................................................................1分
,
,
,.....................................................................3分代入公式可得相关系数 ...................4分
由于 且r非常接近1,所以y与x具有很强的线性相关关系.
经计算可得 ,
..........................................................................................................6分
所以所求线性回归方程为 ......................................................................................7分
(2)(ⅰ)当 时, ,所以预计能带动的消费达35.25百万元. 9分
(ⅱ)因为 %,所以发放的该轮消费券助力消费复苏不是理想的................11分
发放消费券只是影响消费的其中一个因素,还有其他重要因素,
比如:A城市经济发展水平不高,居民的收入水平直接影响了居民的消费水平;
A城市人口数量有限、商品价格水平、消费者偏好、消费者年龄构成等因素一定程度上影响了消费总量.
(只要写出一个原因即可)............................................................................................................12分
19.(12分)如图所示,在直四棱柱 中, , ,且 , ,
,M是 的中点.
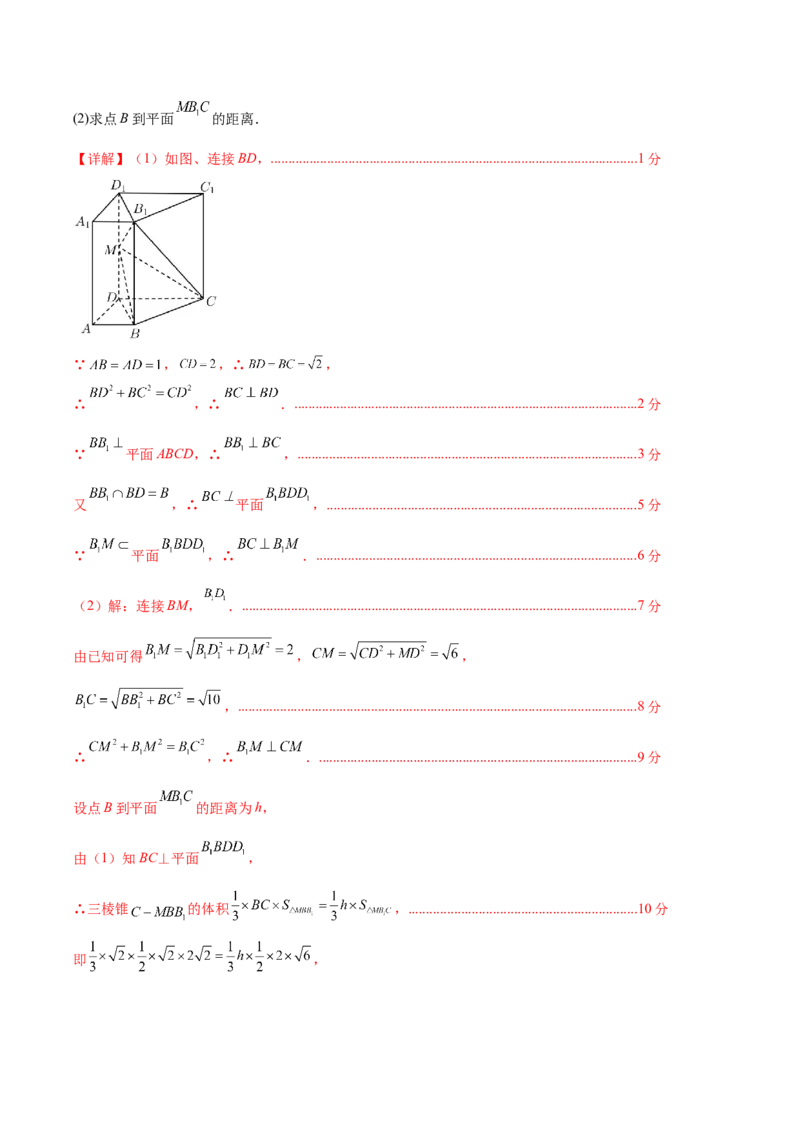
(1)证明 ;(2)求点B到平面 的距离.
【详解】(1)如图、连接BD,........................................................................................................1分
∵ , ,∴ ,
∴ ,∴ ...................................................................................................2分
∵ 平面ABCD,∴ ,.................................................................................................3分
又 ,∴ 平面 ,........................................................................................5分
∵ 平面 ,∴ ............................................................................................6分
(2)解:连接BM, ..................................................................................................................7分
由已知可得 , ,
,..................................................................................................................8分
∴ ,∴ ............................................................................................9分
设点B到平面 的距离为h,
由(1)知BC⊥平面 ,
∴三棱锥 的体积 ,.................................................................10分
即 ,解得 ,即点B到平面 的距离为 .......................................................................12分
20.(12分)已知函数 .
(1)当 时,求函数的单调区间和极值
(2)若 在区间 内恰好有两个零点,求 的取值范围.
【详解】(1)由 得 ,且定义域为 .......................1分
∵ ,令 ,即 ,解得 ,
令 ,解得 ,..........................................................................................................3分
则 的单调递增区间为 ,单调递减区间为 ;..................................................4分
在 处的极小值为 ,无极大值.........................................................6分
(2)当 , 恒成立, 在 上单调递增,.................................................7分
故 在区间 内至多只有一个零点;.....................................................................................8分
当 时,由(1)得 在 上最小值为 ,......................................10分
若 在区间 内恰有两个零点,则需满足 ,整理得 ......................12分
21.(12分)已知椭圆 : 的焦点为 ,离心率为 ,点 为其上动点,且三角
形 的面积最大值为 , 为坐标原点.
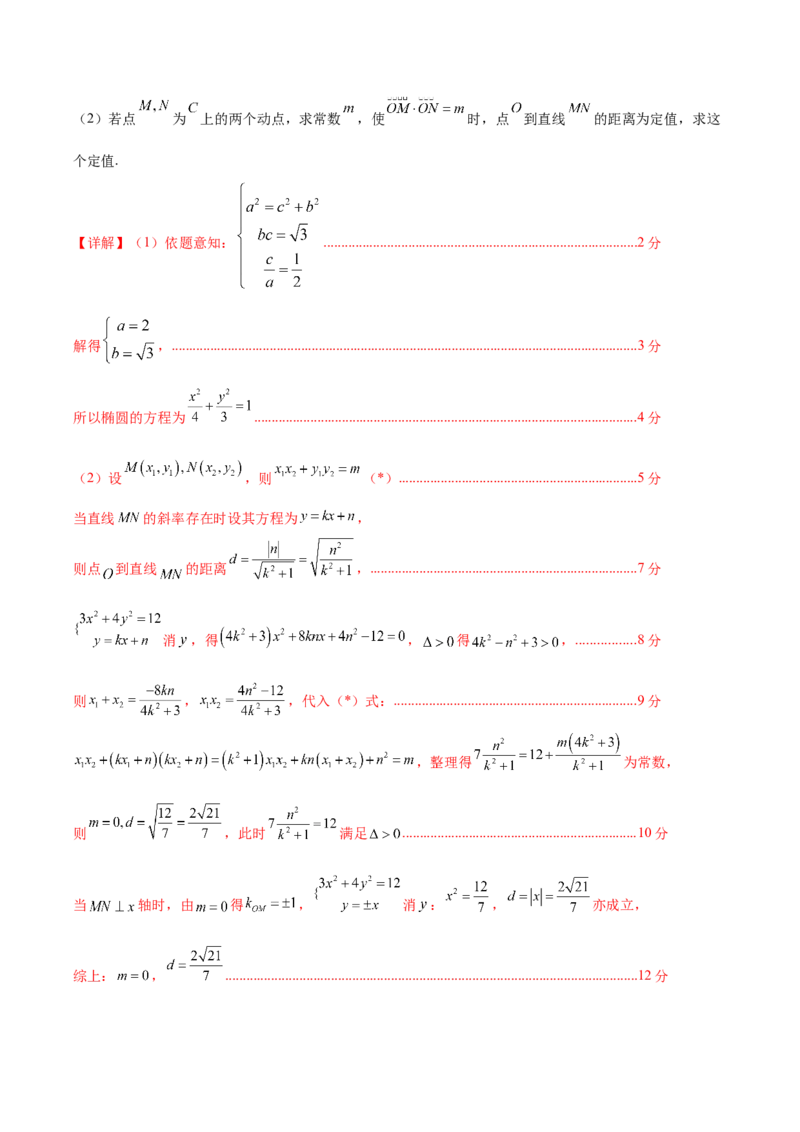
(1)求椭圆的 的方程;(2)若点 为 上的两个动点,求常数 ,使 时,点 到直线 的距离为定值,求这
个定值.
【详解】(1)依题意知: .........................................................................................2分
解得 ,.....................................................................................................................................3分
所以椭圆的方程为 .............................................................................................................4分
(2)设 ,则 (*)....................................................................5分
当直线 的斜率存在时设其方程为 ,
则点 到直线 的距离 ,............................................................................7分
消 ,得 , 得 ,.................8分
则 , ,代入(*)式:.....................................................................9分
,整理得 为常数,
则 ,此时 满足 ...................................................................10分
当 轴时,由 得 , 消 : , 亦成立,
综上: , .....................................................................................................................12分(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)已知曲线 的参数方程分别为 ( 为参数), ( 为参
数).
(1)将 的参数方程化为普通方程;
(2)以坐标原点 为极点,以 轴的非负半轴为极轴,建立极坐标系.若射线 与曲线 分别
交于 两点(异于极点),点 ,求 的面积.
【详解】(1)因为曲线 的参数方程为 (t为参数),
则 , ,.....................................................................................................2分
两式相减,得 的普通方程为: ;
曲线 的参数方程为 ( 为参数),
所以 的普通方程为: ............................................................................................4分
(2)因为 ,
所以曲线 的极坐标方程为 ,即 ,.................5分
联立 ,得 ,
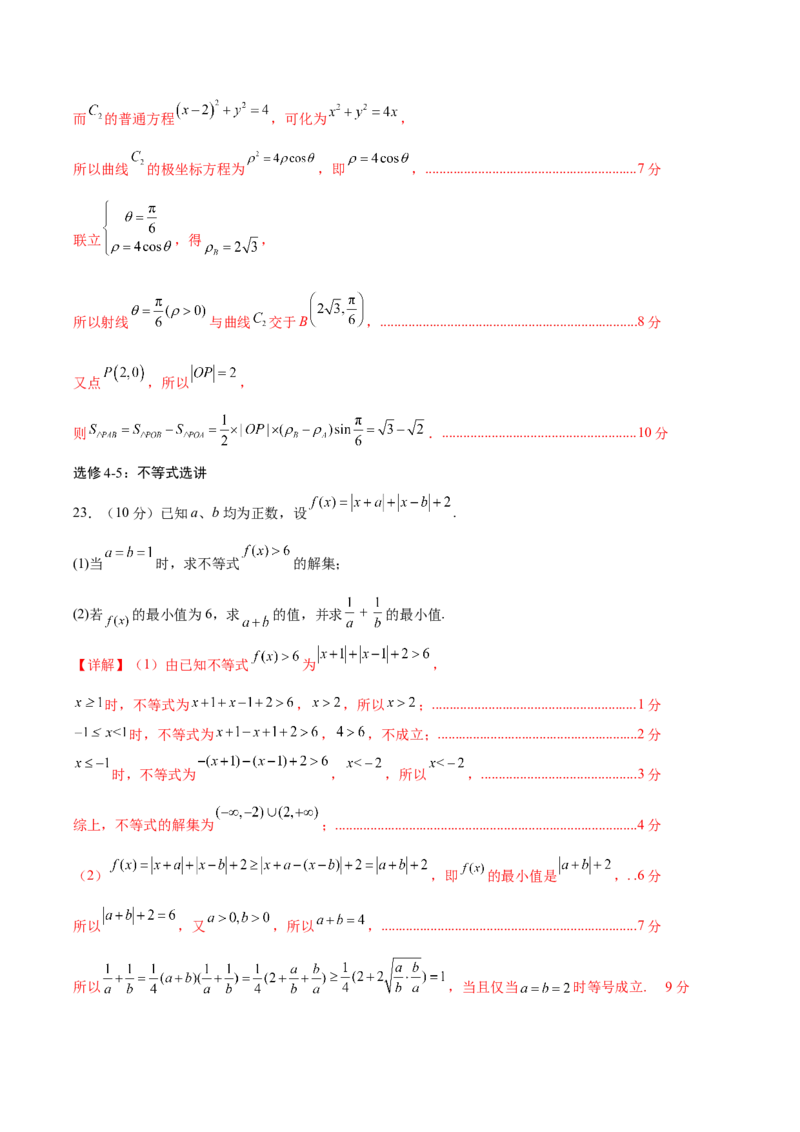
所以射线 与曲线 交于A ,.........................................................................6分而 的普通方程 ,可化为 ,
所以曲线 的极坐标方程为 ,即 ,............................................................7分
联立 ,得 ,
所以射线 与曲线 交于B ,.........................................................................8分
又点 ,所以 ,
则 ........................................................10分
选修4-5:不等式选讲
23.(10分)已知a、b均为正数,设 .
(1)当 时,求不等式 的解集;
(2)若 的最小值为6,求 的值,并求 的最小值.
【详解】(1)由已知不等式 为 ,
时,不等式为 , ,所以 ;..........................................................1分
时,不等式为 , ,不成立;.........................................................2分
时,不等式为 , ,所以 ,............................................3分
综上,不等式的解集为 ;......................................................................................4分
(2) ,即 的最小值是 ,..6分
所以 ,又 ,所以 ,.........................................................................7分
所以 ,当且仅当 时等号成立. 9分所以所求最小值为1..............................................................................................................................10分