2024届福建省三明市普通高中高三毕业班5月质量检测数学参考答案_2024年5月_01按日期_8号_2024届福建省三明市高三下学期三模_福建省三明市普通高中2024届高三毕业班5月质量检测数学试题

三明市 2024 年普通高中高三毕业班质量检测 数学参考答案及评分细则 评分说明： 1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内 容比照评分标准制定相应的评分细则． 2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度， 可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答 有较严重的错误，就不再给分． 3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数．选择题和填空题不给中间分． 一、选择题：本大题考查基础知识和基本运算．每小题5分，满分40分． 1．C 2．C 3．D 4．A 5．A 6．B 7．B 8．C 二、选择题：本大题考查基础知识和基本运算．每小题6分，满分18分．全部选对的得6分， 部分选对的得部分分，有选错的得0分． 9．BC 10．ACD 11．BCD 三、填空题：本大题考查基础知识和基本运算．每小题5分，满分15分． 1  12． 6 13．  ,3  14．  6,7,8,9  , 21 （第一空2分，第二空3分） e  四、解答题：本大题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 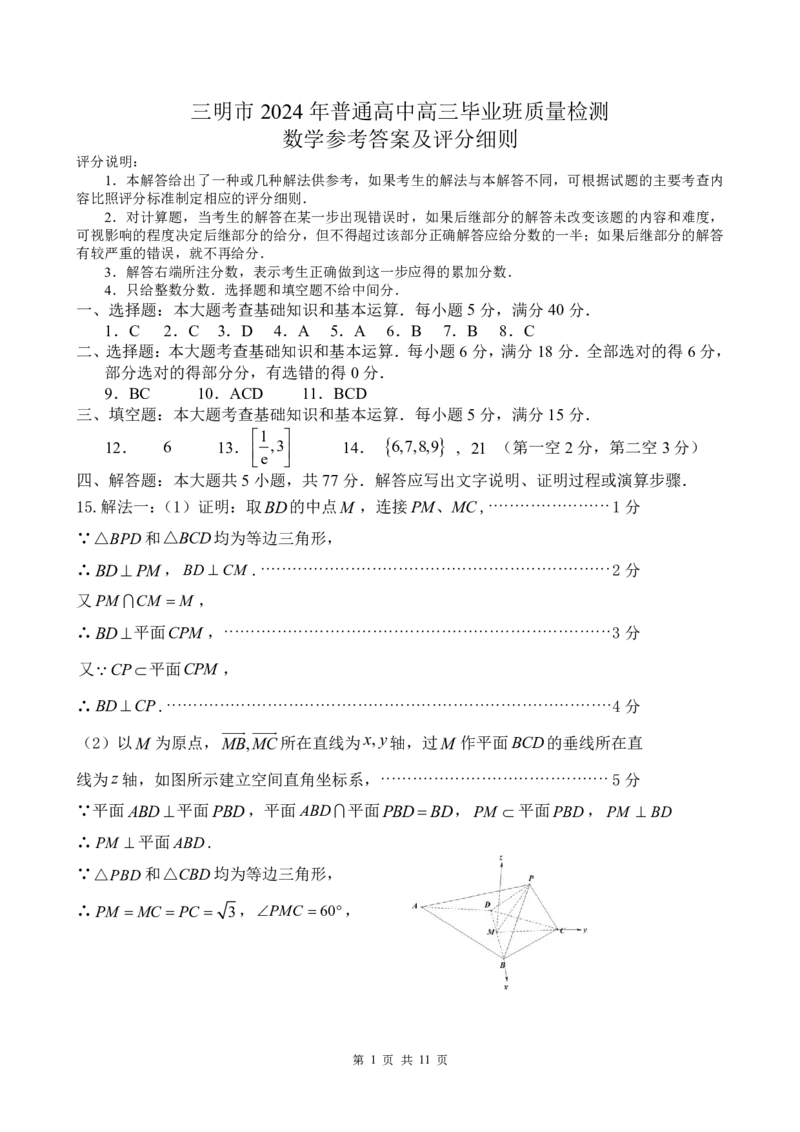15.解法一：（1）证明：取BD的中点M ，连接PM、MC,·······················1分 ∵△BPD和△BCD均为等边三角形， ∴BDPM，BD CM .··································································2分 又PM CM M ， ∴BD平面CPM ，·········································································3分 又CP平面CPM ， ∴BDCP.····················································································4分   （2）以M 为原点，MB,MC所在直线为x,y轴，过M 作平面BCD的垂线所在直 线为z轴，如图所示建立空间直角坐标系，···········································5分 ∵平面ABD平面PBD，平面ABD平面PBDBD，PM 平面PBD，PM  BD ∴PM 平面ABD. ∵△PBD和△CBD均为等边三角形， ∴PM MC  PC  3，PMC 60， 第 1 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#}∴P  0, 3 , 3 ，C  0, 3,0  ，B  1,0,0 ，··············································6分    2 2   3 3      3 3 ∴BP 1, , ，BC  1, 3,0 .MP 0, ,       2 2  2 2 设平面PBC 的法向量为m (x,y,z)   3 3  mBP 0, x y z 0, ∴  即 2 2 mBC 0  x 3y 0   取z 1,则m  3, 3,1 ，···································································8分   3 3 平面ABD的法向量MP 0, , ，·················································10分    2 2 设平面ABD与平面PBC 的夹角为，   MPn 3 39 ∴cos cos MP,n     ··································12分 MP n 3 13 13 39 ∴平面ABD与平面PBC 夹角的余弦值为 .····································13分 13 解法二：（1）同解法一······································································4分 （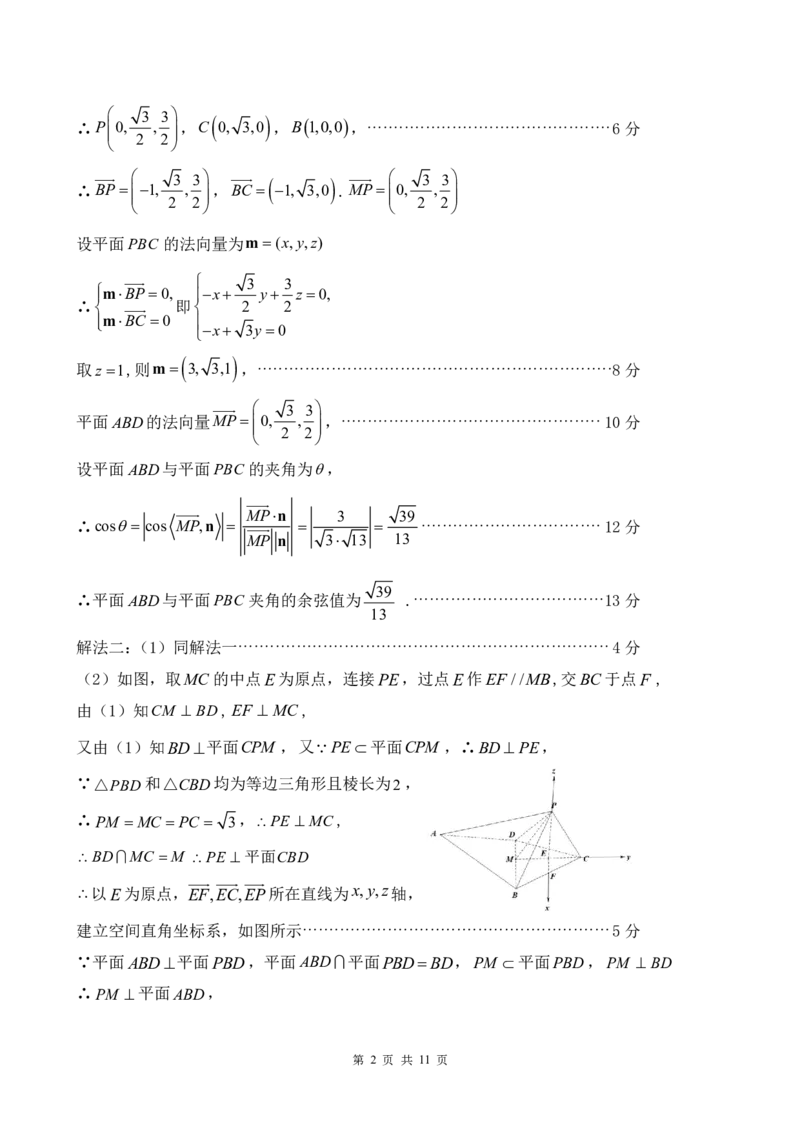2）如图，取MC 的中点E为原点，连接PE，过点E作EF //MB,交BC于点F , 由（1）知CM  BD,EF  MC, 又由（1）知BD平面CPM ，又PE平面CPM ，∴BDPE， ∵△PBD和△CBD均为等边三角形且棱长为2， ∴PM MC  PC  3，PE  MC, BDMC  M PE 平面CBD    以E为原点，EF,EC,EP所在直线为x,y,z轴， 建立空间直角坐标系，如图所示··························································5分 ∵平面ABD平面PBD，平面ABD平面PBDBD，PM 平面PBD，PM  BD ∴PM 平面ABD， 第 2 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#}  3 3 平面ABD的法向量MP 0, , ···················································7分    2 2  3  3   3  ∴P0,0, ，C  0, ,0  ，B  1, ,0  ·············································8分  2  2   2       3 3 ∴CB  1, 3,0 ，CP 0, , ，    2 2 设平面PBC 的法向量为m  x,y,z ，   x 3y 0  mCP 0    ∴  ,即 3 3 ，取z 1,则m  3, 3,1 ，················· 10分 mCB 0  y z 0  2 2 设平面ABD与平面PBC 的夹角为，   MPm 3 39 ∴cos cos MP,m     ，······························12分 MP m 3 13 13 39 ∴平面ABD与平面PBC 夹角的余弦值为 .····································13分 13 16.解法一：  1 3  （1）由题意 f(x)sinxcos(x ) sinx cosxsin(x ) 6 2 2 3 ·····································································································2分 π 因为 f  x 图象的两条相邻对称轴间的距离为 ， 2 所以周期T  2π 2 π ，故2，所以 f  x sin  2x π ，·····················4分  2  3 π π π 当x 0,m 时，2x   ,2m ，·················································5分 3 3 3 π π 3π 因为 f  x 在区间 0,m 上有最大值无最小值，所以 2m  ，·········6分 2 3 2 π 7π  π 7π 解得 m ，所以m的取值范围为 , .···································7分 12 12 12 12 第 3 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#} （2）将函数 f  x 图象向右平移 个单位长度， 6    得到 y sin  2(x )  sin2x的图象，············································8分  6 3 再将图象上所有点的横坐标变为原来的2倍（纵坐标不变）， 得到g(x)sinx的图象，···································································9分 1 1 所以函数h(x) xsinx，所以h(x) cosx，································10分 2 2 1 令h(x)0得cosx ， 2 因为x(2,)， 4 所以当x(2, )时，h(x)0，h(x)单调递增，····························11分 3 4 2 当x( , )时，h(x)0，h(x)单调递减，································ 12分 3 3 2 2 当x( , )时，h(x)0，h(x)单调递增，·································· 13分 3 3 2 当x( ,)时，h(x)0，h(x)单调递减.·········································14分 3 4 2 所以函数h(x)的极大值点为 和 .··············································15分 3 3 解法二：（1）同解法一.····································································· 7分  （2）将函数 f  x 图象向右平移 个单位长度， 6    得到 y sin  2(x )  sin2x的图象，············································8分  6 3 再将图象上所有点的横坐标变为原来的2倍（纵坐标不变）， 得到g(x)sinx的图象，···································································9分 第 4 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#}1 1 所以函数h(x) xsinx，所以h(x) cosx，································10分 2 2 1 令h(x)0得cosx ， 2 2 2 当 2k x 2k时，h(x)0，h(x)单调递增， 3 3 因为x(2,) 4 所以k 1时，2 x ，h(x)单调递增，··································11分 3 2 2 k 1时，  x h(x)单调递增·················································12分 3 3 2 4 当 2k x 2k时，h(x)0，h(x)单调递减， 3 3 因为x(2,) 2 k 0时，  x，h(x)单调递减，·············································· 13分 3 4 2 k 1时，  x ，h(x)单调递减，······································ 14分 3 3 4 2 所以函数h(x)的极大值点为 和 .··············································15分 3 3 解法三：（1）同解法一.····································································· 7分  （2）将函数 f  x 图象向右平移 个单位长度， 6    得到 y sin  2(x )  sin2x的图象，············································8分  6 3 再将图象上所有点的横坐标变为原来的2倍（纵坐标不变）， 得到g(x)sinx的图象，···································································9分 1 1 所以函数h(x) xsinx，所以h(x) cosx，································10分 2 2 第 5 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#}1 令h(x)0得cosx 2 因为x(2,)，所以x,h(x),h(x)的变化情况如下： 4 4 4 2 2 2 2 2 2 x (2, )  ( , )  ( , ) ( ,) 3 3 3 3 3 3 3 3 3 h(x)  0  0  0  极大 极小 极大 h(x) 单调递增 单调递减 单调递增 单调递减 值 值 值 ···································································································14分 4 2 所以函数h(x)的极大值点为 和 .··············································15分 3 3 17.解: (1)记随机任选1题为家政、 园艺、 民族工艺试题分别为事件A(i 1,2,3)， i 记随机任选1题，甲答对为事件B，··············································1分 3 则P(B)P(A)P(B| A)P(A)P(B| A)P(A )P(B| A )P(A )P(B| A ) i i 1 1 2 2 3 3 i1 ······························································································ 2分 1 2 1 2 1 4 3        ,·······························································4分 4 5 4 5 2 5 5 3 所以随机任选1题，甲答对的概率为 ；···········································5分 5 (2) 乙答对记为事件C,则 1 1 1 1 1 1 1 P(C) P(A)P(C| A)P(A )P(C| A )P(A )P(C| A )       1 1 2 2 3 3 4 2 4 2 2 2 2 ·····································································································7分 设每一轮比赛中甲得分为X , 3  1 3 则P(X 1) P(BC) P(B)P(C)  1   ，································· 8分 5  2 10 3 1  3  1 1 P(X 0) P(BCBC) P(BC)P(BC)   1   1   ，········9分 5 2  5  2 2 第 6 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#} 3 1 1 P(X 1) P(BC) 1    .····················································10分  5 2 5 三轮比赛后，设甲总得分为Y , 3  3  27 则P(Y 3)    ，······························································11分 10 1000 2  3  1 27 P(Y 2)C2     ，··························································12分 3 10 2 200 2 2 3 1  3  1 279 P(Y 1)C1    C2     ，··································· 13分 3 10 2 3 10 5 1000 所以甲最终获得奖品的概率为 27 27 279 441 P  P(Y 3)P(Y 2)P(Y 1)    .····················15分 1000 200 1000 1000 18.（1）因为a a a a ( 2)n2n① 1 2 n1 n 所以当n2,a a a a ( 2)(n1)2n1②，·············································1分 1 2 n n1 ② 由 得a 2n··················································································2分 ① n 因为n1时a 2也符合上式，···························································· 3分 1 所以数列a 是以2为首项，2为公比的等比数列， n 所以a 2n,nN*.············································································· 4分 n 2  12n （2）由（1）知， S   2n12 ，···············································5分 n 12 因为不等式(1)ntS 14S 2对任意的 nN恒成立，又S 0且S 单调递增， n n n n ·····································································································6分 14 所以(1)ntS n  S 对任意的 nN恒成立，··········································· 7分 n 因为S =2，S 6，S =14，S =30，·························································· 8分 1 2 3 4 14  14 所以当n为偶数时，原式化简为tS n  S 对任意的 nN恒成立，即t  S n  S   n n min 25 因为S 6 14，所以当n2时，t ，············································10分 2 3 第 7 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#}14  14 当n为奇数时，原式化简为tS n  S 对任意的 nN恒成立，即t  S n  S   n n min 因为S 2 14S 14，所以当n1时，t9，所以t9，··················12分 1 3 25 综上可知，9t .······································································ 13分 3 1 1 （3）因为b   ，······························································14分 n log a 2 2n 2 n 所以b 是单调递减数列， n 所以 b  b ···············································································15分 n1 n b b 2(b b ) 2(b b ) 所以 n n1  n n1  n n1 2( b  b ) b 2 b b  b n n1 n n n n1 b b b b b b 1 2  2 3 + n n1 2( b  b  b  b  b  b ) 1 2 2 3 n n1 b b b 1 2 n 1 2  2 2 原不等式得证.················································································17分  1 1 y  19.解法一：（1）由题意可知双曲线y 的实轴为y  x，联立 x ， x  y  x x1 x 1 1 解得 或 ，即双曲线y 的两顶点为(1,1),(1,1)， y 1 y 1 x 故实轴长2a   11 2  11 2 2 2，即 a 2····································2分 1  函数y 的图象绕原点O顺时针旋转 后渐近线为y x，····················3分 x 4 1 所以 ab 2 ，c2， 所以，双曲线y 的离心率 e 2.·················· 4分 x 1  （2）由（1）知函数y 的图象绕原点O顺时针旋转 得到双曲线x2  y2  2的图象， x 4  1 所以，双曲线x2  y2  2的图象绕原点O逆时针旋转 得到函数y 的图象， 4 x ·····································································································5分 第 8 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#}1 其渐近线分别为x轴和 y轴，此时设P(x , )， 0 x 0 1 因为y ，················································································6分 x2 1 1 1 所以P处切线斜率k  ，P处切线方程为y  (xx ) ，·········7分 x2 x x2 0 0 0 0 2 过P作切线分别交两条渐近线于A(0, ),B(2x ,0)·································· 8分 x 0 0 1 1 2 所以S  OAOB   2x 2， AOB 2 2 x 0 0 所以AOB的面积为定值2，即AOB的面积为定值2.·····························9分 3 3 3 （3）依题意知，函数 y  x 的两条渐近线分别为y  x和y轴， 3 2x 3 则实轴为 y  3x  3 3  x  3 y  x  2 由 3 2x ,联立解得 ，所以双曲线实半轴长a  3，   3  y  3x y   2 3 3  x2 将函数 y  x 的图象绕原点O顺时针旋转 得到曲线的方程为  y2 1， 3 2x 3 3 ···································································································10分  将F(1, 3),直线l:x 3y30绕原点O顺时针旋转 得到 3 3 F(2,0)，直线l:x  ·····································································11分 2 则过F(2,0)直线交曲线右支于M,N两点， 3 3 设M(x ,y )，N(x ,y )，则C( ,y )，D( ,y ) 1 1 2 2 2 1 2 2 因为直线MN斜率不为0，所以设直线MN方程为x my2， x my2,  由x2 得(m2 3)y2 4my10，   y2 1  3 第 9 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#} 4m y  y  , m2 30,   1 2 m2 3  且 ··························································12分   0  1 y y   1 2 m2 3 因为 y y 0，所以m2 3，·····························································13分 1 2 y  y y y 3 k  2 1 y y  2 1 (x ) 因为 NC 3 ，所以NC方程为 1 3 2 ， x  x  2 2 2 2 3 1 y (x  ) my y  y 令 y 0得 1 2 2 3 1 2 2 1 3 x     y  y 2 y  y 2 2 1 2 1 y  y 由韦达定理可得my y  1 2 ， 1 2 4 y  y 1 1 2  y 所以 4 2 1 3 1 3 7 x      y  y 2 4 2 4 2 1 7 7 所以直线NC过定点( ,0)，由图象的对称性可知，MD过定点( ,0)， 4 4 7 即直线NC与直线MD交点H( ,0)，··············································15分 4 1 1 1 3 m2 1 那么S  HF y  y    (y  y )2 4y y   MNH 2 1 2 2 4 1 2 1 2 4 (m2 3)2 ···································································································16分 令t m2 1，则1t 4， m2 1 t 1   则 (m2 3)2 (t4)2 16 t 8 t 16 因为函数 y t 8在 1,4 上单调递减 t 3 1 3 所以当t 1，即m2 0时，MNH面积取最小值，最小值为   ， 4 9 12 3 1 3 即MNH面积最小值为   .················································ 17分 4 9 12 解法二： 第 10 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#}（1）同解法一.················································································4分 （2）当曲线E在点P处切线斜率不存在时，切线方程为 x  2,此时AOB面积为2， ·····································································································5分 当曲线E在点P处切线斜率存在时，设在点P处切线方程为 y kxm， y kxm, 联立 得(1k2)x2 2kmxm2 20， x2  y2 2 1k2 0, 则 ,化简得m2 2k2 2,k2 1···················· 6分  4k2m2 4(1k2)(m2 2)0 y kxm, m m 由 得A( , )，  y  x 1k 1k y kxm, m m 由 得B( , ).····························································7分  y x 1k 1k m m m m 4m2(1k2) 4 1k2 则 AB  (  )2 (  )2   ， 1k 1k 1k 1k 1k2 m m 因为原点O到直线y kxm的距离d  ，···································8分 1k2 1 1 4 1k2 m 所以S  AB d  2， AOB 2 2 m 1k2 所以AOB面积为定值2.····································································9分 （3）同解法一.·············································································· 17分 第 11 页 共 11 页 {#{QQABDYaEoggoAJJAABhCQQUgCkAQkAEAAKoGwAAIMAAAiBFABCA=}#}