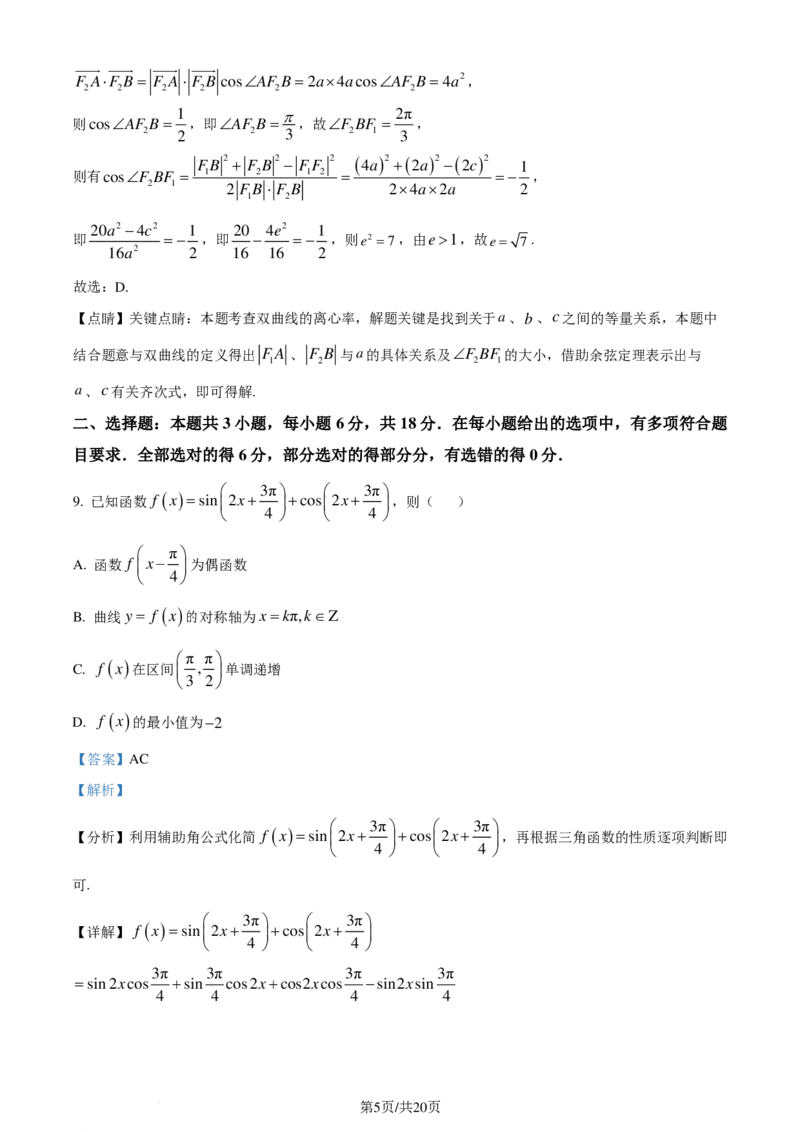2024年1月普通高等学校招生全国统一考试适应性测试（九省联考）数学试题（解析版）(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套

2024 年 1 月普通高等学校招生全国统一考试适应性测试（九省联考） 数学试题 注意事项： ]．答卷前，考生务必将自己的考生号、姓名、考点学校、考场号及座位号填写在答题卡上． 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需要 改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写在 本试卷上无效． 3．考试结束后，将本试卷和答题卡一并交回． 一、选择题：本题共 8小题，每小题 5分，共 40分．在每小题给出的四个选项中，只有一项 是符合题目要求的． 1. 样本数据16，24，14，10，20，30，12，14，40的中位数为（ ） A. 14 B. 16 C. 18 D. 20 【答案】B 【解析】 【分析】由中位数定义即可得. 【详解】将这些数据从小到大排列可得：10，12，14，14，16，20，24，30，40， 则其中位数为16. 故选：B. 2. 椭圆 x2 + y2 =1(a >1)的离心率为 1 ，则a =（ ） a2 2 2 3 A. B. 2 C. 3 D. 2 3 【答案】A 【解析】 【分析】由椭圆的离心率公式即可求解. a2 −1 1 2 3 【详解】由题意得e= = ，解得a= ， a 2 3 故选：A. 3. 记等差数列 { a } 的前n项和为S ,a +a =6,a =17，则S =（ ） n n 3 7 12 16 A. 120 B. 140 C. 160 D. 180 第1页/共20页 学科网（北京）股份有限公司【答案】C 【解析】 【分析】利用下标和性质先求出a +a 的值，然后根据前n项和公式结合下标和性质求解出S 的值. 5 12 16 【详解】因为a +a =2a =6，所以a =3，所以a +a =3+17=20， 3 7 5 5 5 12 ( a +a )×16 所以S = 1 16 =8 ( a +a )=160， 16 2 5 12 故选：C. 4. 设α,β是两个平面，m,l 是两条直线，则下列命题为真命题的是（ ） A. 若α⊥β,m∥α,l∥β，则m⊥l B. 若m⊂α,l ⊂β,m∥l，则α∥β C. 若αβ=m,l∥α,l∥β，则m∥l D. 若m ⊥α,l ⊥β,m∥l，则α⊥β 【答案】C 【解析】 【分析】由线面平行性质判断真命题，举反例判定假命题即可. 【详解】对于A，m,l 可能平行，相交或异面，故A错误，对于B，α,β可能相交或平行，故B错误， 对于D，α,β可能相交或平行，故D错误，由线面平行性质得C正确， 故选：C 5. 甲、乙、丙等5人站成一排，且甲不在两端，乙和丙之间恰有2人，则不同排法共有（ ） A. 20种 B. 16种 C. 12种 D. 8种 【答案】B 【解析】 【分析】分类讨论：乙丙及中间2人占据首四位、乙丙及中间2人占据尾四位，然后根据分类加法计数原理 求得结果. 【详解】因为乙和丙之间恰有2人，所以乙丙及中间2人占据首四位或尾四位， ①当乙丙及中间2人占据首四位，此时还剩末位，故甲在乙丙中间， 排乙丙有A2种方法，排甲有A1种方法，剩余两个位置两人全排列有A2种排法， 2 2 2 所以有A2×A1 ×A2 =8种方法； 2 2 2 ②当乙丙及中间2人占据尾四位，此时还剩首位，故甲在乙丙中间， 第2页/共20页 学科网（北京）股份有限公司排乙丙有A2种方法，排甲有A1种方法，剩余两个位置两人全排列有A2种排法， 2 2 2 所以有A2×A1 ×A2 =8种方法； 2 2 2 由分类加法计数原理可知，一共有8816种排法， 故选：B.  6. 已知Q为直线l:x+2y+1=0上的动点，点P满足QP =( 1,−3 )，记P的轨迹为E，则（ ） A. E是一个半径为 5的圆 B. E是一条与l相交的直线 C. E上的点到l的距离均为 5 D. E是两条平行直线 【答案】C 【解析】  【分析】设P ( x,y ) ，由QP =( 1,−3 )可得Q点坐标，由Q在直线上，故可将点代入坐标，即可得P轨迹E， 结合选项即可得出正确答案.  【详解】设P ( x,y ) ，由QP =( 1,−3 )，则Q ( x−1,y+3 ) ， 由Q在直线l:x+2y+1=0上，故x−1+2 ( y+3 )+1=0， 化简得x+2y+6=0，即P的轨迹为E为直线且与直线l平行， 6−1 E上的点到l的距离d = = 5，故A、B、D错误，C正确. 12 +22 故选：C. 3π   π 1+sin2θ 7. 已知θ∈  ,π,tan2θ=−4tan θ+ ，则 =（ ）  4   4 2cos2θ+sin2θ 1 3 3 A. B. C. 1 D. 4 4 2 【答案】A 【解析】 1+sin2θ 【分析】根据正弦、余弦、正切二倍角公式，将 齐次化即可得出答案. 2cos2θ+sin2θ 3π   π 【详解】由题θ∈  ,π,tan2θ=−4tan θ+ ，  4   4 第3页/共20页 学科网（北京）股份有限公司2tanθ −4 ( tanθ+1 ) 得 = ⇒−4 ( tanθ+1 )2 =2tanθ， 1−tan2θ 1−tanθ 1 则 ( 2tanθ+1 )( tanθ+2 )=0⇒tanθ=−2或tanθ=− ， 2 3π  1 因为θ∈  ,π,tanθ∈(−1,0 ) ，所以tanθ=− ，  4  2 1+sin2θ sin2θ+cos2θ+2sinθcosθ tan2θ+1+2tanθ = = 2cos2θ+sin2θ 2cos2θ+2sinθcosθ 2+2tanθ 1 +1−1 1 4 . = = 2+(−1 ) 4 故选：A x2 y2 8. 设双曲线C: − =1(a>0,b>0)的左、右焦点分别为F,F ，过坐标原点的直线与C交于A,B两点， a2 b2 1 2   FB =2 FA,F A⋅F B =4a2，则C的离心率为（ ） 1 1 2 2 A. 2 B. 2 C. 5 D. 7 【答案】D 【解析】 【分析】由双曲线的对称性可得 FA = F B 、FB = F A 且四边形AFBF 为平行四边形，由题意可得出 1 2 1 2 1 2 ∠F BF ，结合余弦定理表示出与a、c有关齐次式即可得离心率. 2 1 【详解】 由双曲线的对称性可知 FA = F B ， FB = F A ，有四边形AFBF 为平行四边形， 1 2 1 2 1 2 令 FA = F B =m，则 FB = F A =2m， 1 2 1 2 由双曲线定义可知 F A − FA =2a，故有2m−m=2a，即m=2a， 2 1 即 FA = F B =m=2a， FB = F A =4a， 1 2 1 2 第4页/共20页 学科网（北京）股份有限公司    F A⋅F B= F A ⋅ F B cos∠AF B=2a×4acos∠AF B=4a2， 2 2 2 2 2 2 1 π 2π 则cos∠AF B= ，即∠AF B= ，故∠F BF = ， 2 2 2 3 2 1 3 FB 2 + F B 2 − FF 2 ( 4a )2 +( 2a )2 −( 2c )2 1 则有cos∠F BF = 1 2 1 2 = =− ， 2 1 2 FB ⋅ F B 2×4a×2a 2 1 2 20a2 −4c2 1 20 4e2 1 即 =− ，即 − =− ，则e2 =7，由e>1，故e= 7. 16a2 2 16 16 2 故选：D. 【点睛】关键点睛：本题考查双曲线的离心率，解题关键是找到关于a、b、c之间的等量关系，本题中 结合题意与双曲线的定义得出 FA 、 F B 与a的具体关系及∠F BF 的大小，借助余弦定理表示出与 1 2 2 1 a、c有关齐次式，即可得解. 二、选择题：本题共 3小题，每小题 6分，共 18分．在每小题给出的选项中，有多项符合题 目要求．全部选对的得 6分，部分选对的得部分分，有选错的得 0分．  3π  3π 9. 已知函数 f ( x )=sin2x+  +cos2x+ ，则（ ）  4   4   π A. 函数 f x− 为偶函数  4 B. 曲线y = f ( x ) 的对称轴为x=kπ,k∈Z π π ( ) C. f x 在区间 , 单调递增 3 2 ( ) D. f x 的最小值为−2 【答案】AC 【解析】  3π  3π 【分析】利用辅助角公式化简 f ( x )=sin2x+  +cos2x+ ，再根据三角函数的性质逐项判断即  4   4  可.  3π  3π 【详解】 f ( x )=sin2x+  +cos2x+   4   4  3π 3π 3π 3π =sin2xcos +sin cos2x+cos2xcos −sin2xsin 4 4 4 4 第5页/共20页 学科网（北京）股份有限公司2 2 2 2 =− sin2x+ cos2x− cos2x− sin2x=− 2sin2x， 2 2 2 2 即 f ( x )=− 2sin2x，  π  π 对于A， f x−  =− 2sin2x−  = 2cos2x，易知为偶函数，所以A正确；  4  2 π π kπ 对于B， f ( x )=− 2sin2x对称轴为2x= +kπ,k∈Z⇒ x= + ,k∈Z，故B错误； 2 4 2 π π 2π  对于C，x∈ , ,2x∈ ,π，y =sin2x单调递减，则 3 2  3  f ( x )=− 2sin2x单调递增，故C正确； 对于D， f ( x )=− 2sin2x，则sin2x∈[−1,1 ] ，所以 f ( x )∈− 2, 2，故D错误；   故选：AC 10. 已知复数z,w均不为0，则（ ） z z2 A. z2 =| z|2 B. = z |z|2 z z = C. z−w= z−w D. w w 【答案】BCD 【解析】 【分析】设出z =a+bi、w=c+di，结合复数的运算、共轭复数定义及复数的模的性质逐个计算即可得. 【详解】设z =a+bi ( a,b∈R ) 、w=c+di ( c,d∈R ) ； 对A：设z =a+bi ( a,b∈R ) ，则z2 =( a+bi )2 =a2 +2abi−b2 =a2 −b2 +2abi， ( )2 |z|2= a2 +b2 =a2 +b2，故A错误； z z2 z z2 对B： = ，又z⋅z = z 2，即有 = ，故B正确； z z⋅z z |z|2 对C：z−w=a+bi−c−di=a−c+( b−d ) i，则z−w=a−c−( b−d ) i， z =a−bi，w=c−di，则z−w=a−bi−c+di=a−c−( b−d ) i， 即有z−w= z−w，故C正确； 第6页/共20页 学科网（北京）股份有限公司z a+bi ( a+bi )( c−di ) ac+bd −( ad −bc ) i 对D： = = = w c+di ( c+di )( c−di ) c2 +d2 ac+bd  2 ad −bc 2 a2c2 +2abcd +b2d2 +a2d2 −2abcd +b2c2 = + =      c2 +d2   c2 +d2  ( c2 +d2 )2 a2c2 +b2d2 +a2d2 +b2c2 a2c2 +b2d2 +a2d2 +b2c2 = = ， ( c2 +d2 )2 c2 +d2 ( )( ) z a2 +b2 a2 +b2 × c2 +d2 a2 +b2 c2 +d2 = = = w c2 +d2 c2 +d2 c2 +d2 a2c2 +b2c2 +a2d2 +b2d2 = ， c2 +d2 z z 故 = ，故D正确. w w 故选：BCD. 1 11. 已知函数 f ( x ) 的定义域为R，且 f   ≠0，若 f ( x+ y )+ f ( x ) f ( y )=4xy，则（ ） 2  1 1 A. f  −  =0 B. f   =−2  2 2  1  1 C. 函数 f x− 是偶函数 D. 函数 f x+ 是减函数  2  2 【答案】ABD 【解析】 1 1 【分析】对抽象函数采用赋值法，令x= 、y=0，结合题意可得 f ( 0 )=−1，对 A：令x= 、y=0， 2 2 1  1  1  1 代入计算即可得；对B、C、D：令y =− ，可得 f x−  =−2x，即可得函数 f x− 及函数 f x+  2  2  2  2 1 函数的性质，代入x=1，即可得 f  . 2 1 1 1 1 【详解】令x= 、y=0，则有 f   + f   × f ( 0 )= f     1+ f ( 0 )  =0， 2 2 2 2 1 又 f   ≠0，故1+ f ( 0 )=0，即 f ( 0 )=−1， 2 第7页/共20页 学科网（北京）股份有限公司1 1 1 1 1  1 1  1 令x= 、y =− ，则有 f  −  + f   f  −  =4× ×  − ， 2 2 2 2 2  2 2  2 1  1 1  1 即 f ( 0 )+ f   f  −  =−1，由 f ( 0 )=−1，可得 f   f  −  =0， 2  2 2  2 1  1 又 f   ≠0，故 f  −  =0，故A正确； 2  2 1  1  1  1 令y =− ，则有 f x−  + f ( x ) f  −  =4x×  − ， 2  2  2  2  1  1 即 f x−  =−2x，故函数 f x− 是奇函数，  2  2  1  1 有 f x+1−  =−2 ( x+1 )=−2x−2，即 f x+  =−2x−2，  2  2  1 即函数 f x+ 是减函数，  2 1 令x=1，有 f   =−2×1=−2， 2 故B正确、C错误、D正确. 故选：ABD. 【点睛】关键点睛：本题关键在于利用赋值法解决抽象函数问题，借助赋值法，得到 f ( 0 )=−1，再重新  1  1 赋值，得到 f  −  =0，再得到 f x−  =−2x.  2  2 三、填空题：本题共 3小题，每小题 5分，共 15分． 12. 已知集合A={−2,0,2,4 } ,B= { x x−3 ≤m } ，若AB = A，则m的最小值为__________． 【答案】5 【解析】 【分析】由AB = A可得A⊆B，解出集合B后结合集合的关系计算即可得. 【详解】由AB = A，故A⊆B， 由 x−3 ≤m，得−m+3≤ x≤m+3， 4≤m+3 m≥1 故有 ，即 ，即m≥5， −2≥−m+3 m≥5 第8页/共20页 学科网（北京）股份有限公司即m的最小值为5. 故答案为：5. 13. 已知轴截面为正三角形的圆锥MM′的高与球O的直径相等，则圆锥MM′的体积与球O的体积的比值 是__________，圆锥MM′的表面积与球O的表面积的比值是__________． 2 【答案】 ①. ②. 1 3 【解析】 【分析】设圆锥的底面圆半径r以及球的半径R，用r表示出圆锥的高h和母线l以及球的半径R，然后根 据体积公式求出体积比，根据表面积公式求得表面积之比. 【详解】设圆锥的底面半径为r，球的半径为R， 因为圆锥的轴截面为正三角形，所以圆锥的高h = 3r，母线l =2r， 3 由题可知：h=2R，所以球的半径R= r 2 所以圆锥的体积为V = 1 × ( π×r2 ) × 3r = 3 πr3， 1 3 3 3 4 4  3  3 球的体积V = πR3 = π× r = πr3， 2 3 3   2   2 3 πr3 V 3 2 所以 1 = = ； V 3 3 2 πr3 2 圆锥的表面积S =πrl+πr2 =3πr2， 1 2  3  球的表面积S =4πR2 =4π× r =3πr2， 2   2   S 3πr2 所以 1 = =1， S 3πr2 2 2 故答案为： ；1. 3 14. 以 maxM 表 示 数 集 M 中 最 大 的 数 ． 设 00， b=1−n− p 所以 ， a =1−m−n− p 若b≥2a，则b=1−n− p≥2 ( 1−m−n− p ) ，故2m+n+ p≥1， 令M=max { b−a,c−b,1−c }=max { m,n,p } ， 2M ≥2m  1 因此M ≥n ,故4M ≥2m+n+ p≥1,则M ≥ ，  4 M ≥ p 若a+b≤1，则1−n− p+1−m−n− p≤1，即m+2n+2p≥1， M=max { b−a,c−b,1−c }=max { m,n,p } ， M ≥m  1 则2M ≥2n ,故5M ≥m+2n+2p≥1,则M ≥ ，  5 2M ≥2p 当m=2n=2p时，等号成立， 1 综上可知max { b−a,c−b,1−c } 的最小值为 ， 5 1 故答案为： 5 【点睛】关键点睛：本题的关键是利用换元法，在b≥2a和a+b≤1前提下进行合理分类讨论，根据题意 得到相对应的不等式组，注意题目的条件关键词是“或”. 四、解答题：本题共 5小题，共 77分．解答应写出文字说明、证明过程或演算步骤． 15. 已知函数 f ( x )=lnx+ x2 +ax+2在点 ( 2,f ( 2 )) 处的切线与直线2x+3y =0垂直． （1）求a； （2）求 f ( x )的单调区间和极值． 【答案】（1）a=−3 （2）单调递增区间为  0, 1 、 ( 1,+∞) ，单调递减区间为   1 ,1  ，极大值 3 −ln2，极小值0  2 2  4 第10页/共20页 学科网（北京）股份有限公司【解析】 【分析】（1）结合导数的几何意义及直线垂直的性质计算即可得； （2）借助导数可讨论单调性，即可得极值. 【小问1详解】 1 1 9 f′( x )= +2x+a，则 f′( 2 )= +2×2+a = +a， x 2 2 9   2 由题意可得 +a ×  −  =−1，解得a=−3； 2   3 【小问2详解】 由a=−3，故 f ( x )=lnx+x2 −3x+2， 1 2x2 −3x+1 ( 2x−1 )( x−1 ) 则 f′( x )= +2x−3= = ，x>0， x x x 1 1 故当01时， fx0， 2 2 故 f ( x ) 的单调递增区间为  0, 1 、 ( 1,+∞) ， f ( x ) 的单调递减区间为   1 ,1  ，  2 2  2 ( ) 1 1 1 1 3 故 f x 有极大值 f   =ln +   −3× +2= −ln2， 2 2 2 2 4 有极小值 f ( 1 )=ln1+12 −3×1+2=0. 16. 盒中有标记数字1，2，3，4的小球各2个，随机一次取出3个小球． （1）求取出的3个小球上的数字两两不同的概率； ( ) （2）记取出的3个小球上的最小数字为X ，求X 的分布列及数学期望E X ． 4 【答案】（1） 7 10 （2）分布列见解析，E ( X )= 7 【解析】 【分析】（1）先确定3个不同数字的小球，然后再从确定的每种小球中取1个，通过计算可求符合要求的取 法数，再除以总的取法数可得结果； （2）先确定X 的可取值为1,2,3，然后计算出不同取值的概率，注意X 的每种取值对应两种情况，由此可 ( ) 求分布列和期望E X . 第11页/共20页 学科网（北京）股份有限公司【小问1详解】 记“取出的3个小球上的数字两两不同”为事件M ， 先确定3个不同数字的小球，有C3种方法， 4 然后每种小球各取1个，有C1 ×C1 ×C1种取法， 2 2 2 C3×C1 ×C1 ×C1 4 所以P ( M )= 4 2 2 2 = . C3 7 8 【小问2详解】 由题意可知，X 的可取值为1,2,3， 当X =1时，分为两种情况：只有一个数字为1的小球、有两个数字为1的小球， C1C2 +C2C1 9 所以P ( X =1 )= 2 6 2 6 = ； C3 14 8 当X =2时，分为两种情况：只有一个数字为2的小球、有两个数字为2的小球， C1C2 +C2C1 2 所以P ( X =2 )= 2 4 2 4 = ； C3 7 8 当X =3时，分为两种情况：只有一个数字为3的小球、有两个数字为3的小球， C1C2 +C2C1 1 所以P ( X =3 )= 2 2 2 2 = ， C3 14 8 所以X 的分布列为： X 1 2 3 9 2 1 P 14 7 14 9 2 1 10 所以E ( X )=1× +2× +3× = . 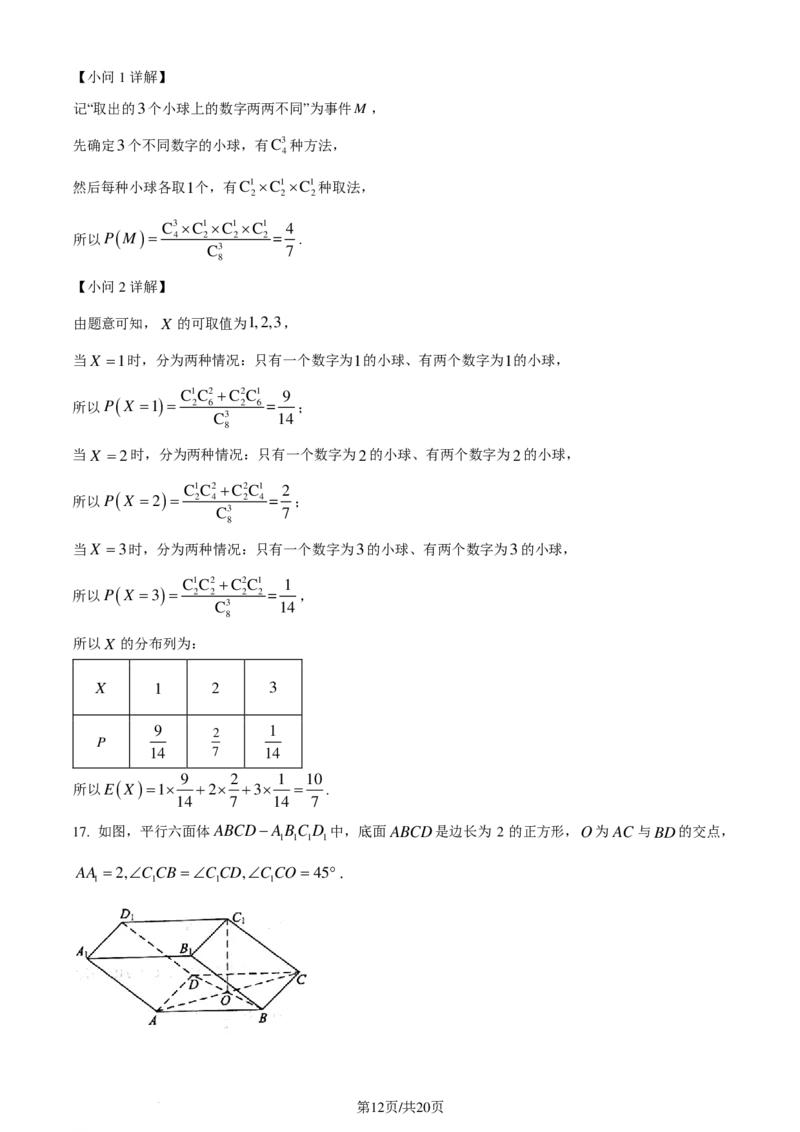14 7 14 7 17. 如图，平行六面体ABCD−ABC D 中，底面ABCD是边长为 2 的正方形，O为AC与BD的交点， 1 1 1 1 AA =2,∠CCB =∠CCD,∠CCO =45°． 1 1 1 1 第12页/共20页 学科网（北京）股份有限公司（1）证明：CO⊥平面ABCD； 1 （2）求二面角B−AA −D的正弦值． 1 【答案】（1）证明见解析； 2 2 （2） 3 【解析】 【分析】（1）根据题意，利用线面垂直的判定定理证明即可. （2）建立空间直角坐标系，利用向量法求二面角的正弦值. 【小问1详解】 连接BC ,DC ， 1 1 因为底面ABCD是边长为2的正方形，所以BC = DC， 又因为 ∠CCB=∠CCD，CC =CC ， 1 1 1 1 所以CCB≅CCD，所以BC = DC ， 1 1 1 1 点O为线段BD中点，所以CO⊥ BD， 1 1 在△CCO中，CC =2,CO= AC = 2 ，∠CCO=45°， 1 1 2 1 2 CC2 +OC2 −CO2 所以cos∠CCO= = 1 1 ⇒CO= 2 ， 1 2 2×CC×OC 1 1 则CC2 =OC2 +CO2 ⇒CO⊥OC， 1 1 1 又OCBD=O，OC ⊂平面ABCD，BD⊂平面ABCD， 所以CO⊥平面ABCD. 1 【小问2详解】 第13页/共20页 学科网（北京）股份有限公司由题知正方形ABCD中AC⊥BD，CO⊥平面ABCD，所以建系如图所示， 1 ( ) ( ) ( ) ( ) ( ) 则B 0, 2,0 ,D 0,− 2,0 ,A 2,0,0 ,C − 2,0,0 ,C 0,0, 2 ， 1   ( ) 则AA =CC = 2,0, 2 ， 1 1   ( ) ( ) AB= − 2, 2,0 ,AD= − 2,− 2,0 ，   设面BAA 的法向量为m=( x ,y ,z )，面DAA 的法向量为n=( x ,y ,z )， 1 1 1 1 1 2 2 2    AA ⋅m=0   2x + 2z =0  则1  ⇒ 1 1 ⇒m=( 1,1,−1 ) ， AB⋅m=0  − 2x + 2y =0 1 1    AA ⋅n =0   2x + 2z =0  1  ⇒ 2 2 ⇒n =( 1,−1,−1 ) ， AD⋅m=0  − 2x − 2y =0 2 2 设二面角B−AA −D大小为θ， 1   m⋅n 1 1 2 2 则cosθ=   = = ⇒sinθ= 1−cos2θ= ， m ⋅ n 3× 3 3 3 2 2 所以二面角B−AA −D的正弦值为 . 1 3 18. 已知抛物线C: y2 =4x的焦点为F ，过F 的直线l交C于A,B两点，过F 与l垂直的直线交C于D,E 两点，其中B,D在x轴上方，M,N 分别为AB,DE的中点． （1）证明：直线MN 过定点； （2）设G为直线AE与直线BD的交点，求GMN 面积的最小值． 【答案】（1）证明见解析 （2）8 第14页/共20页 学科网（北京）股份有限公司【解析】 【分析】（1）设出直线AB与直线CD的方程，联立曲线后得到与纵坐标有关韦达定理，结合题意，表示出 直线MN 后即可得定点坐标； （2）设出直线AE与直线BD的方程，联立两直线后结合第一问中韦达定理得出点G的横坐标恒为−1，再 结合面积公式及基本不等式即可得. 【小问1详解】 由C: y2 =4x，故F ( 1,0 ) ，由直线AB与直线CD垂直， 故两只直线斜率都存在且不为0， 设直线AB、CD分别为x =m y+1、x=m y+1，有mm =−1， 1 2 1 2 A ( x ,y ) 、B ( x ,y ) 、E ( x ,y ) 、D ( x ,y ) ， 1 1 2 2 3 3 4 4 y2 =4x 联立C: y2 =4x与直线AB，即有 ， x=m y+1 1 消去x可得y2 −4m y−4=0，∆=16m2 +16>0， 1 1 故y + y =4m 、y y =−4， 1 2 1 1 2 则x +x =m y +1+m y +1=m ( y + y )+2=4m2 +2， 1 2 1 1 1 2 1 1 2 1 x +x y + y 故 1 2 =2m2 +1， 1 2 =2m ， 2 1 2 1 ( ) ( ) 即M 2m2 +1,2m ，同理可得N 2m2 +1,2m ， 1 1 2 2 当2m2 +1≠2m2 +1时， 1 2 2m −2m ( ) l : y = 2 1 x−2m2 −1 +2m 则 MN 2m2 +1− ( 2m2 +1 ) 1 1 ， 2 1 即y = m 2 −m 1 ( x−2m2 −1 ) +2m = x − 2m 1 2 +1 + 2m 1 ( m 2 +m 1 ) m2 −m2 1 1 m +m m +m m +m 2 1 2 1 2 1 2 1 x 2m2 +1−2mm −2m2 x 1−2mm = − 1 1 2 1 = − 1 2 ， m +m m +m m +m m +m 2 1 2 1 2 1 2 1 x 1+2 1 由mm =−1，即y = − = ( x−3 ) ， 1 2 m +m m +m m +m 2 1 2 1 2 1 1 故x=3时，有y = ( 3−3 )=0， m +m 2 1 第15页/共20页 学科网（北京）股份有限公司( ) 此时MN 过定点，且该定点为 3,0 ， 当2m2 +1=2m2 +1时，即m2 =m2时，由mm =−1，即m =±1时， 1 2 1 2 1 2 1 有l :x=2+1=3，亦过定点 ( 3,0 ) ， MN ( ) 故直线MN 过定点，且该定点为 3,0 ； 【小问2详解】 由A ( x ,y ) 、B ( x ,y ) 、E ( x ,y ) 、D ( x ,y ) ， 1 1 2 2 3 3 4 4 y − y 则l : y = 3 1( x−x )+ y ，由y2 =4x 、y2 =4x ， AE x −x 1 1 1 1 2 2 3 1 y − y  y2  4x y2 y2 + y y 4x y y y = 3 1 x− 1 + y = − 1 + 1 1 3 = + 1 3 故 y2 y2  4  1 y + y y + y y + y y + y y + y ， 3 − 1 3 1 3 1 3 1 3 1 3 1 4 4  4x y y y = + 1 3  4x y y  y + y y + y 同理可得l : y = + 2 4 ，联立两直线，即 3 1 3 1 ， BD y + y y + y 4x y y 4 2 4 2  y = + 2 4   y + y y + y 4 2 4 2 4x y y 4x y y 有 + 1 3 = + 2 4 ， y + y y + y y + y y + y 3 1 3 1 4 2 4 2 即4x ( y + y )+ y y ( y + y )=4x ( y + y )+ y y ( y + y ) ， 4 2 1 3 4 2 3 1 2 4 3 1 y y ( y + y )− y y ( y + y ) 有x= 2 4 3 1 1 3 4 2 ，由y y =−4，同理y y =−4， 4 ( y + y − y − y ) 1 2 3 4 4 2 3 1 第16页/共20页 学科网（北京）股份有限公司y y ( y + y )− y y ( y + y ) y y y + y y y − y y y − y y y 故x= 2 4 3 1 1 3 4 2 = 2 3 4 1 2 4 1 3 4 1 2 3 4 ( y + y − y − y ) 4 ( y + y − y − y ) 4 2 3 1 4 2 3 1 −4 ( y + y − y − y ) = 2 4 1 3 =−1， 4 ( y + y − y − y ) 4 2 3 1 故x =−1， G 1 过点G作GQ//x轴，交直线MN 于点Q，则S = y − y × x −x ， GMN 2 M N Q G ( ) ( ) 由M 2m2 +1,2m 、N 2m2 +1,2m ， 1 1 2 2 2 2 故 y − y =2m −2m =2m + ≥2 2m × =4， M N 1 2 1 m 1 m 1 1 当且仅当m =±1时，等号成立， 1 下证 x −x ≥4： Q G 由抛物线的对称性，不妨设m >0，则m <0， 1 2 1 当m >1时，有m =− ∈(−1,0 ) ，则点G在x轴上方，点Q亦在x轴上方， 1 2 m 1 1 1 = >0 有m +m 1 ，由直线MN 过定点 ( 3,0 ) ， 2 1 m − 1 m 2 此时 x −x >3−(−1 )=4， Q G 同理，当m <1时，有点G在x轴下方，点Q亦在x轴下方， 1 1 有 <0，故此时 x −x >4， m +m Q G 2 1 当且仅当m =1时，x =3， 1 Q 故 x −x ≥4恒成立，且m =±1时，等号成立， Q G 1 1 1 故S = y − y × x −x ≥ ×4×4=8， GMN 2 M N Q G 2 第17页/共20页 学科网（北京）股份有限公司【点睛】关键点睛：第二问关键在于借助直线联立及第一问中韦达定理得出点G的横坐标恒为−1，此时可 根据三角形的面积公式及基本不等式求取最值. 19. 离散对数在密码学中有重要的应用．设 p是素数，集合X ={ 1,2,,p−1 } ，若u,v∈X,m∈N，记u⊗v 为 uv 除以 p 的余数， um,⊗ 为 um 除以 p 的余数；设 a∈X ，1,a,a2,⊗,,ap−2,⊗ 两两不同，若 an,⊗ =b ( n∈{ 0,1,,p−2 }) ，则称n是以a为底b的离散对数，记为n =log(p) b． a （1）若 p =11,a =2，求ap−1,⊗； （2）对m ,m ∈{ 0,1,,p−2 } ，记m ⊕m 为m +m 除以 p−1的余数（当m +m 能被 p−1整除时， 1 2 1 2 1 2 1 2 m ⊕m =0）．证明：log(p) ( b⊗c )=log(p) b⊕log(p) c，其中b,c∈X ； 1 2 a a a （3）已知n =log(p) b．对x∈X,k∈{ 1,2,,p−2 } ，令y =ak,⊗,y = x⊗bk,⊗．证明： a 1 2 x = y ⊗ yn(p−2),⊗． 2 1 【答案】（1）1 （2）证明见解析 （3）证明见解析 【解析】 【分析】（1）第一问直接根据新定义来即可. （2）第二问结合新定义、带余除法以及费马小定理即可得证. （3）根据新定义进行转换即可得证. 【小问1详解】 若 p =11,a =2，又注意到210 =1024=93×11+1， 第18页/共20页 学科网（北京）股份有限公司所以ap−1,⊗ =210,⊗ =1. 【小问2详解】 当 p=2时，此时X ={1}，此时b=c=1，b⊗c=1， 故log(p) ( b⊗c )=0,log(p) b=0,log(p) c=0， a a a 此时log(p) ( b⊗c )=log(p) b⊕log(p) c. a a a 当 p>2时，因1,a,a2,⊗,,ap−2,⊗相异，故a≥2， 而a∈X ，故a,p互质. 设n=log(p) ( b⊗c ) ,n =log(p) b,n =log(p) c a 1 a 2 a 记n=log(p) ( b⊗c ) ,n =log(p) b,n =log(p) c， a 1 a 2 a 则∃m ,m ∈N，使得an 1 = pm +b,an 2 = pm +c， 1 2 1 2 故an 1 +n 2 =( pm +b )( pm +c ) ，故an 1 +n 2 ≡bc(mod p)， 1 2 设n +n =t ( p−1 )+s,0≤s≤ p−2，则n ⊕n =s， 1 2 1 2 因为1,2,3,..p−1除以 p的余数两两相异， 且a,2a,3a,.. ( p−1 ) a除以 p的余数两两相异， 故 ( p−1 ) !≡  a×2a×3a,..×( p−1 ) a  (mod p)，故ap−1 ≡1mod p， 故as ≡bc(mod p)，而an ≡b⊗c(mod p)=bc(mod p),其中0≤n≤ p−2， 故s =n即log(p) ( b⊗c )=log(p) b⊕log(p) c. a a a 【小问3详解】 当b≥2时，由（2）可得bp−1 ≡1mod p，若b=1，则bp−1 ≡1mod p也成立. 因为n =log(p) b，所以an ≡b ( mod p ) . a 另一方面，y ⊗yn(p−2),⊗ ≡ y yn(p−2),⊗ ≡ ( x⊗bk,⊗)( ak,⊗)n(p−2) 2 1 2 1 ≡ ( xbk ) akn(p−2) ≡ ( xbk ) bk(p−2) ≡ x ( bp−1 )k−1 ≡ x ( 1 )k−1( mod p )≡ x ( mod p ) . 由于x∈X ，所以x= y ⊗yn(p−2),⊗ . 2 1 【点睛】关键点睛：本题的关键是充分理解新定义，然后结合带余除法以及费马小定理等初等数论知识即 第19页/共20页 学科网（北京）股份有限公司可顺利得解. 第20页/共20页 学科网（北京）股份有限公司