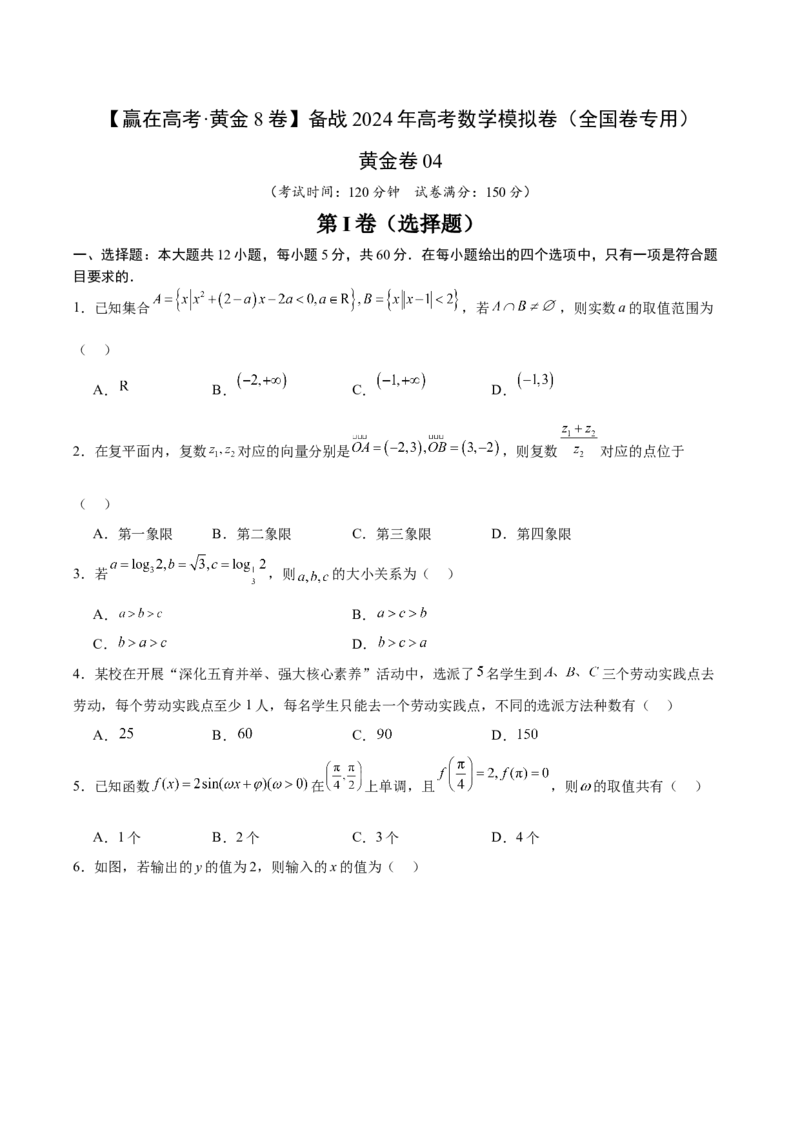文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷04
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.已知集合 ,若 ,则实数a的取值范围为
( )
A. B. C. D.
2.在复平面内,复数 对应的向量分别是 ,则复数 对应的点位于
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若 ,则 的大小关系为( )
A. B.
C. D.
4.某校在开展“深化五育并举、强大核心素养”活动中,选派了 名学生到 三个劳动实践点去
劳动,每个劳动实践点至少1人,每名学生只能去一个劳动实践点,不同的选派方法种数有( )
A. B. C. D.
5.已知函数 在 上单调,且 ,则 的取值共有( )
A.1个 B.2个 C.3个 D.4个
6.如图,若输出的y的值为2,则输入的x的值为( )A. 或4 B.2或6 C. 或6 D.6或4
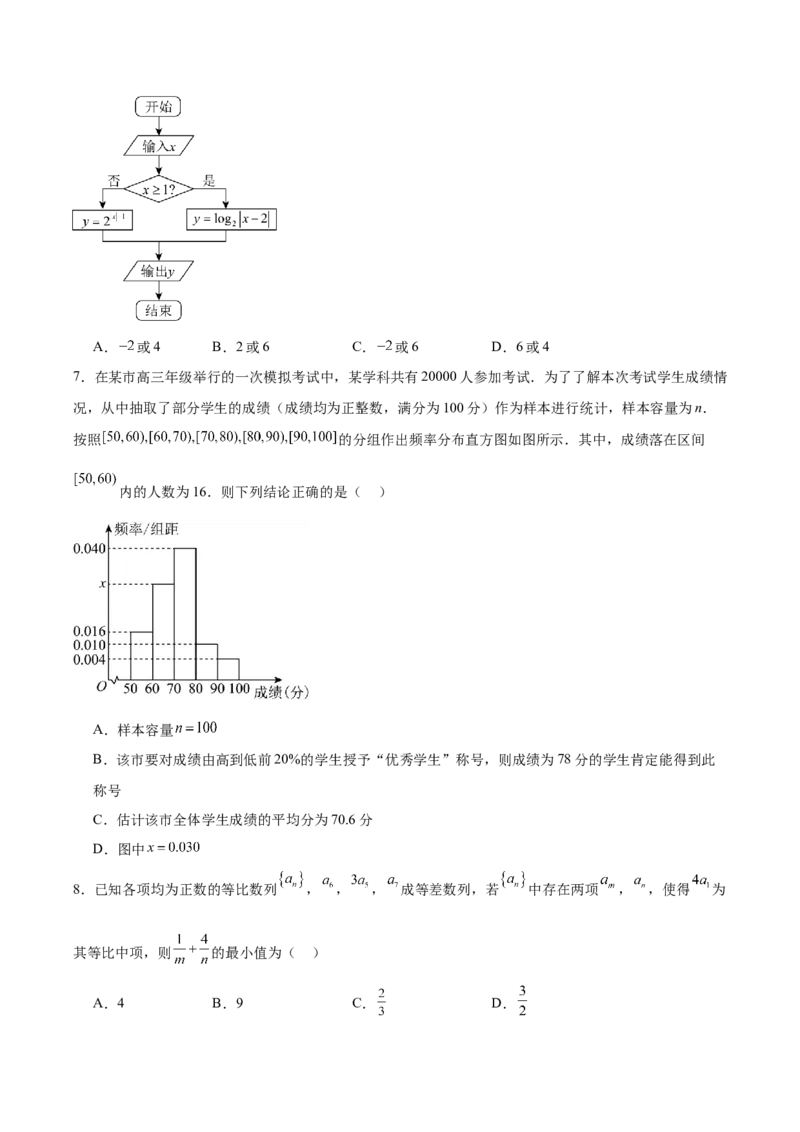
7.在某市高三年级举行的一次模拟考试中,某学科共有20000人参加考试.为了了解本次考试学生成绩情
况,从中抽取了部分学生的成绩(成绩均为正整数,满分为100分)作为样本进行统计,样本容量为n.
按照 的分组作出频率分布直方图如图所示.其中,成绩落在区间
内的人数为16.则下列结论正确的是( )
A.样本容量
B.该市要对成绩由高到低前20%的学生授予“优秀学生”称号,则成绩为78分的学生肯定能得到此
称号
C.估计该市全体学生成绩的平均分为70.6分
D.图中
8.已知各项均为正数的等比数列 , , , 成等差数列,若 中存在两项 , ,使得 为
其等比中项,则 的最小值为( )
A.4 B.9 C. D.9.已知三棱锥 的四个顶点在球O的球面上, , ,E,
F分别是 , 的中点, ,则球O的体积为( )
A.8 B. C. D.
10.“圆幂定理”是平面几何中关于圆的一个重要定理,它包含三个结论,其中一个是相交弦定理:圆内
的两条相交弦,被交点分成的两条线段长的积相等,如图,已知圆 的半径2,点 是圆 内的定点,且
,弦 均过点 ,则下列说法错误的是( )
A. 为定值
B.当 时, 为定值
C. 的取值范围是
D. 的最大值为12
11.已知 分别为双曲线 的左、右焦点,过 与双曲线的一条渐近线平行的直线
交双曲线于点 ,若 ,则双曲线的离心率为( )
A.3 B. C. D.2
12.已知函数 ,(其中 是自然对数的底数),若 在 上恒成立,
则实数m的取值范围为( )
A. B. C. D.
第 II 卷(非选择题)二、填空题:本大题共4小题,每小题5分,共20分
13.已知函数 在 处的切线方程为 ,则 .
14.抛物线 上的动点M到两定点 的距离之和的最小值为 .
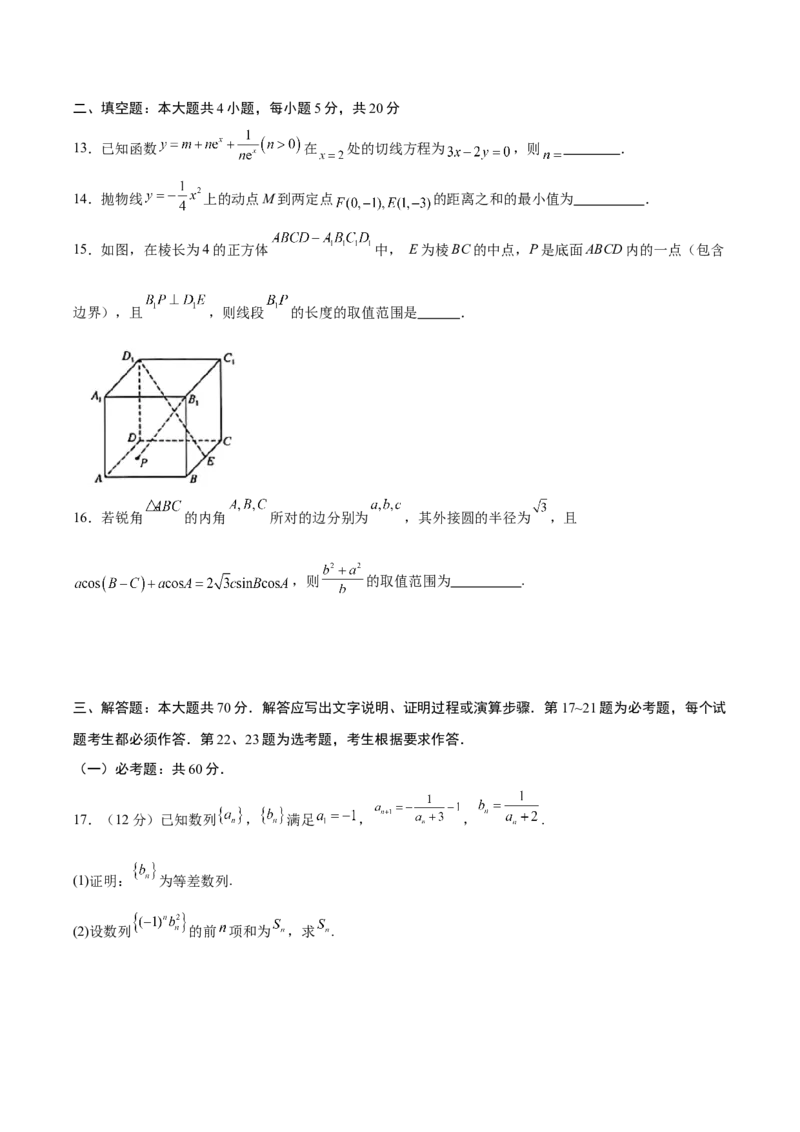
15.如图,在棱长为4的正方体 中, E为棱BC的中点,P是底面ABCD内的一点(包含
边界),且 ,则线段 的长度的取值范围是 .
16.若锐角 的内角 所对的边分别为 ,其外接圆的半径为 ,且
,则 的取值范围为 .
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)已知数列 , 满足 , , .
(1)证明: 为等差数列.
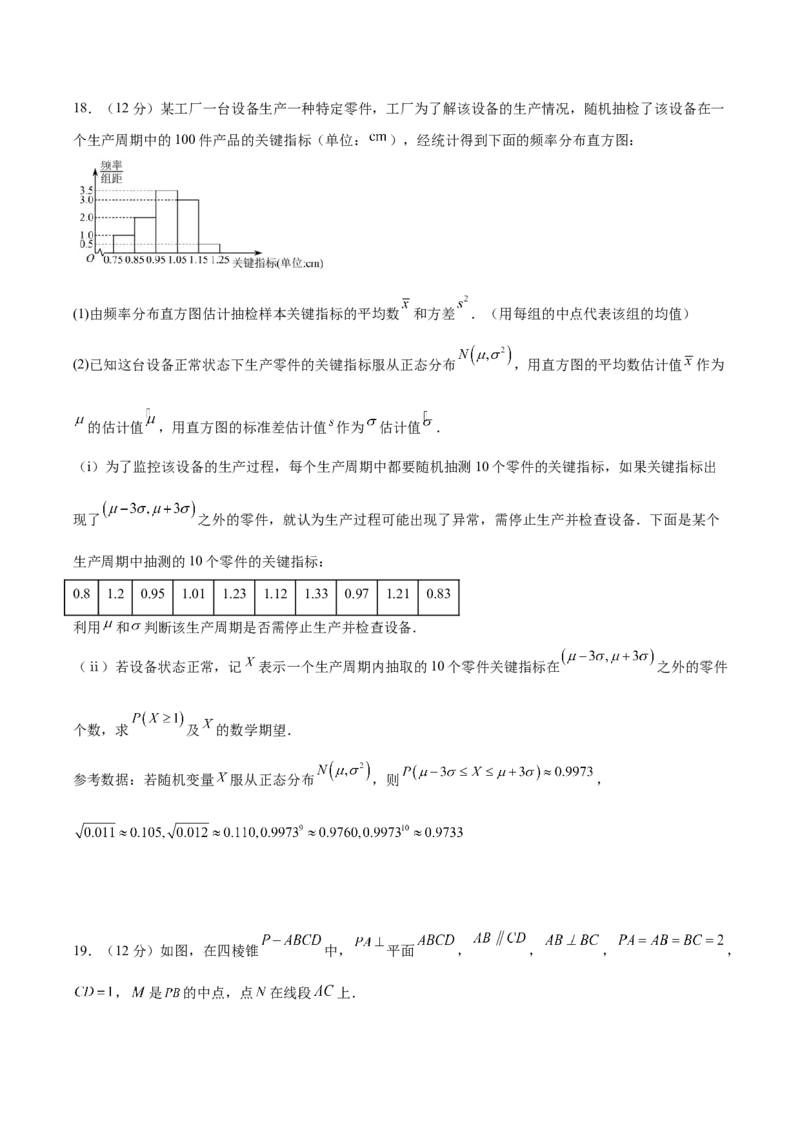
(2)设数列 的前 项和为 ,求 .18.(12分)某工厂一台设备生产一种特定零件,工厂为了解该设备的生产情况,随机抽检了该设备在一
个生产周期中的100件产品的关键指标(单位: ),经统计得到下面的频率分布直方图:
(1)由频率分布直方图估计抽检样本关键指标的平均数 和方差 .(用每组的中点代表该组的均值)
(2)已知这台设备正常状态下生产零件的关键指标服从正态分布 ,用直方图的平均数估计值 作为
的估计值 ,用直方图的标准差估计值 作为 估计值 .
(i)为了监控该设备的生产过程,每个生产周期中都要随机抽测10个零件的关键指标,如果关键指标出
现了 之外的零件,就认为生产过程可能出现了异常,需停止生产并检查设备.下面是某个
生产周期中抽测的10个零件的关键指标:
0.8 1.2 0.95 1.01 1.23 1.12 1.33 0.97 1.21 0.83
利用 和 判断该生产周期是否需停止生产并检查设备.
(ⅱ)若设备状态正常,记 表示一个生产周期内抽取的10个零件关键指标在 之外的零件
个数,求 及 的数学期望.
参考数据:若随机变量 服从正态分布 ,则 ,
19.(12分)如图,在四棱锥 中, 平面 , , , ,
, 是 的中点,点 在线段 上.(1)当 是 中点时,求点 到平面 的距离;
(2)当二面角 的正弦值为 时,求 的值.
20.(12分)已知椭圆 的左、右顶点分别为 ,右焦点为 ,过点 且斜率为 的
直线 交椭圆 于点 .
(1)若 ,求 的值;
(2)若圆 是以 为圆心,1为半径的圆,连接 ,线段 交圆 于点 ,射线 上存在一点 ,使得
为定值,证明:点 在定直线上.
21.(12分)已知函数 ,其中 .
(1)讨论函数 的单调性;
(2)当 时,证明: .(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)( 2023·四川宜宾·统考一模)在平面直角坐标系 中,射线l的方程为 ,曲线
C的方程为 .以坐标原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求射线l和曲线C的极坐标方程;
(2)若射线l与曲线C交于点P,将射线 绕极点按逆时针方向旋转 交C于点Q,求 的面积.
选修4-5:不等式选讲
23.(10分)已知函数 .
(1)当 时,求不等式 的解集;
(2)若 恒成立,求实数m的取值范围.