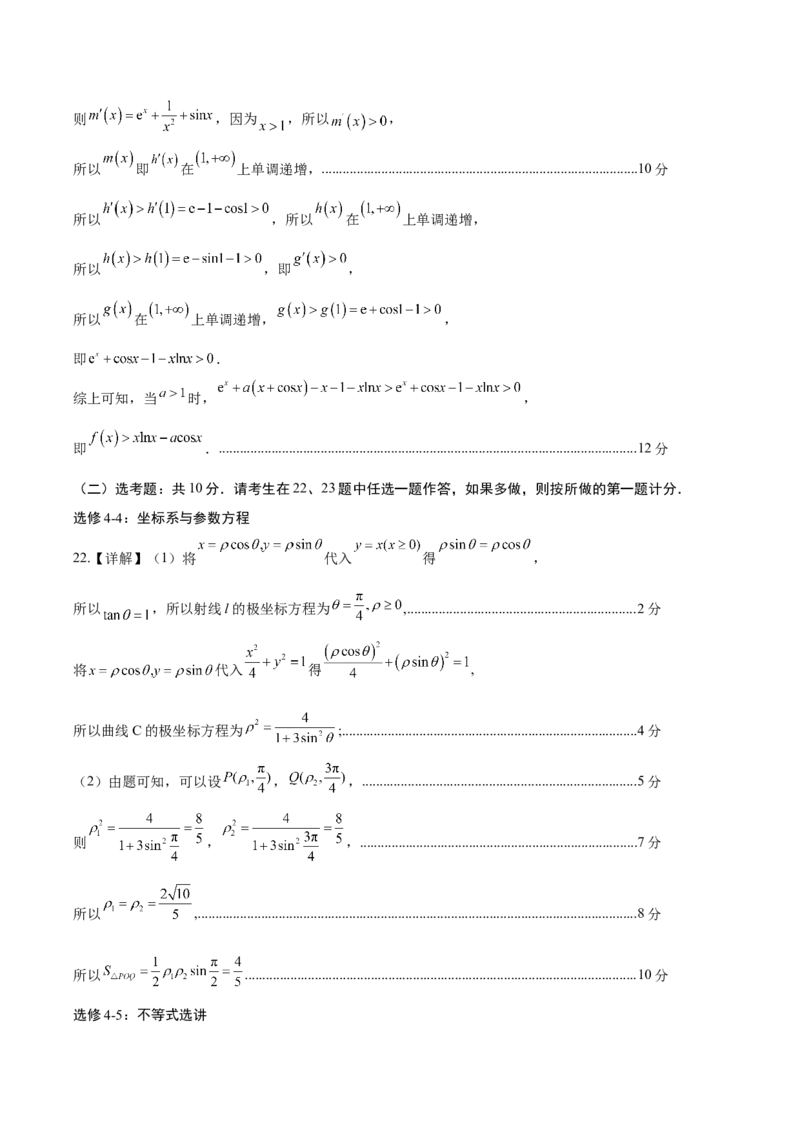文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷04
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1 2 3 4 5 6 7 8 9 10 11 12
C A C D C C B D D D C D
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13. 14.4 15. 16.
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.【详解】(1)由题意得 , ,......................................1分
则 ,........................................3分
所以 是首项 ,公差为1的等差数列. ...................................................................5分
(2)由(1)得 ,则 ,.......................................................7分
当 为偶数时,
..............................................................................9分当 为奇数时, 为偶数,
则 .......................................................................11分
综上, .....................................................................................................................12分
18.【详解】(1)由频率分布直方图,得 . 2分
.........4分
(2)(i)由(1)可知 , ,.....................................................................5分
所以 , ,...........................................................6分
显然抽查中的零件指标 ,故需停止生产并检查设备.................................................7分
(ii)抽测一个零件关键指标在 之内的概率为 ,
所以抽测一个零件关键指标在 之外的概率为 ,
故 ,.........................................................................................................................9分
所以 ,..................................................11分
X的数学期望 ........................................................................................12分
19.【详解】(1)因为 平面 , 平面 ,所以 , .
在平面 内作 ,又 ,所以 两两垂直,......................................1分
以B为坐标原点建立如图所示的空间直角坐标系.............................................................................................................2分
因为 , , ,N是 中点,
则 , , , , , ,
, , .
设平面 的法向量 ,
则 即 取 .................................................................4分
所以点N到平面 的距离 ....................................................................5分
(2)因为M是 的中点,所以 ,设 ,
则 , , ........................................................6分
设平面 的法向量 ,
则 即 取 ............................................7分
设平面 的法向量 ,
则 即 取 ...............................9分设二面角 的大小为 ,则 .
设 ,因为二面角 的正弦值为 ,
所以 ,解得 ,此时 ,..........................................................................11分
所以 ........................................................................................................................................12分
20.【详解】(1)依题意可得 ,可设 , ,
由 ,消去 整理得 ,............................................2分
, ,
, ,
,.......................................................................................................................4分
所以 ,解得 或 (舍去),
所以 ...............................................................................................................................................4分
(2)由(1)知 , ,
若直线 斜率存在,则 , 直线 ,由 得 ,又点 在线段 上,.......................................................5分
所以 ,即 ,又 ,
,...............................................................................................................7分
设 ,则 ,
;
当 时, 为定值,此时 ,则 ,此时 在定直线 上;
当 时, 不为定值,不合题意;.............................................................................9分
若直线 斜率不存在,由椭圆和圆的对称性,不妨设 ,从而有 , ,
此时 ,则直线 ,
设 ,则 , , ,
则 时, ,满足题意;..............................................................................................11分
综上所述:当 为定值,点 在定直线 上................................................................12分21.【详解】(1)因为 ,所以 ,......................................1分
当 时, ,函数 在 上单调递增;...................................................2分
当 时,由 ,得 ,
函数 在区间 上单调递增,
由 ,得 ,函数 在区间 上单调递减........4分
(2)要证 ,即证 ,
即证 ,...........................................................................5分
设 ,
故 在 上单调递增,又 ,所以 ,
又因为 ,所以 ,
所以 ,...................................................................7分
①当 时,因为 ,所以 ;............................8分
②当 时,令 ,则 ,
设 ,则 ,设 ,则 ,因为 ,所以 ,
所以 即 在 上单调递增,..........................................................................................10分
所以 ,所以 在 上单调递增,
所以 ,即 ,
所以 在 上单调递增, ,
即 .
综上可知,当 时, ,
即 ........................................................................................................................12分
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.【详解】(1)将 代入 得 ,
所以 ,所以射线l的极坐标方程为 ,.................................................................2分
将 代入 得 ,
所以曲线C的极坐标方程为 ;....................................................................................4分
(2)由题可知,可以设 , ,..............................................................................5分
则 , ,...............................................................................7分
所以 ,.............................................................................................................................8分
所以 ................................................................................................................10分
选修4-5:不等式选讲23.【详解】(1)由题知,当 时,原不等式即 ,
当 时,不等式为 ,解得 ;.............................................................1分
当 时,不等式为 ,恒成立;...................................................................2分
当 时,不等式为 ,解得 ,........................................................................3分
综上,不等式 的解集为 ;..................................................................................5分
(2)因为 ,...........................................................................7分
当且仅当 时不等式取等号,即 ,
所以 ,解得 ,..........................................................................................9分
所以 的取值范围是 .........................................................................................10分