文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考Ⅰ卷专用)
黄金卷05
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.设集合 ,则 ( )
A. B. C. D.
【答案】C
【分析】解分式不等式、指数函数值域求集合,再由集合的交运算求结果.
【详解】由题设 , ,
所以 .
故选:C
2.设复数 对应的点在第四象限,则复数 对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【分析】由 的周期性化简 ,计算后判断所求复数对应点的象限.
【详解】由复数 对应的点在第四象限,
则设 ,
由
得 ,
由 ,得复数 对应的点在第二象限.
故选:B.
3.在平行四边形 中, 是 的中点, 是 的中点, 与 相交于点 ,则 ( )
A. B. C. D.
【答案】A
【分析】根据题意可知: 为 的重心,结合向量的线性运算结合重心的性质分析求解.
【详解】设 ,
由题意可知: 为 的重心,且 为 的中点,
可知 四点共线,且 ,
所以 .
故选:A.
4.某地投资 亿元进行基础建设, 年后产生的社会经济效益为 亿元,若该地投资基础建设4
年后产生的社会经济效益是投资额的2倍,且再过 年,该项投资产生的社会经济效益是投资额的16倍,
则 ( )
A.4 B.8 C.12 D.16
【答案】C
【分析】由 求出 的值,再令 求出 ,从而求出 .
【详解】依题意 ,显然 ,即 ,所以 ,则 ,所以 ,令 ,即 ,所以 ,
即 ,所以 ,所以该地投资基础建设 年后产生的社会经济效益是投资额的 倍,
所以 .
故选:C
5.某大学强基测试有近千人参加,每人做题最终是否正确相互独立,其中一道选择题有5个选项,假设若
会做此题则必能答对.参加考试的同学中有一部分同学会做此题;有一半的同学完全不会,需要在5个选项
中随机蒙一个选项;剩余同学可以排除一个选项,在其余四个选项中随机蒙一个选项,最终统计该题的正
答率为30%,则真会做此题的学生比例最可能为( )
A.5% B.10% C.15% D.20%
【答案】B
【分析】设测试总人数为 ,真会做此题的学生人数为 ,再由已知列式计算得解.
【详解】设测试总人数为 ,真会做此题的学生人数为 ,
依题意, ,解得 .
故选:B
6.设函数 ,且 在 上单调,则下列
结论不正确的是( )
A. 是 的一个对称中心
B.函数 的图象关于直线 对称
C.函数 在区间 上的值域为
D.先将 的图象的横坐标缩短为原来的 ,然后向左平移 个单位得到 的图象
【答案】C
【分析】先求得 ,然后根据三角函数的对称性、值域、三角函数图象变换等知识求得正确答案.【详解】依题意, , , ,
,
并化简得 , , 是偶数,
由③得 ,所以 ,
代入①得 ,
而 ,所以 ,所以 .
A选项, ,所以 是 的一个对称中心,A选项正确.
B选项, ,所以函数 的图象关于直线 对称,B选项正确.
C选项, ,
所以 ,所以C选项错误.
D选项,先将 的图象的横坐标缩短为原来的 ,得到 ,
然后向左平移 个单位得到 ,
所以D选项正确.
故选:C7.已知 , , ,则( )
A. B.
C. D.
【答案】C
【分析】对 平方可得 ,再构造 ,对 求导,得出 的单调性可
知 ,所以 时, ,即可得比较 的大小,即可得出答案.
【详解】 ,
,∴ .
在B,C中选,比较a,b大小,
令 ,
,
令 , 在 上恒成立,
所以 在 上单调递减,所以 ,所以 ,
所以 在 上单调递减,所以 ,
所以 时, ,则 ,即 ,故 .
故选:C.
8.油纸伞是中国传统工艺品,至今已有1000多年的历史,为宣传和推广这一传统工艺,北京市文化宫开
展油纸伞文化艺术节活动中,某油纸伞撑开后摆放在户外展览场地上,如图所示,该伞伞沿是一个半径为2的圆,圆心到伞柄底端距离为2,当阳光与地面夹角为 时,在地面形成了一个椭圆形影子,且伞柄底
端正好位于该椭圆的长轴上,若该椭圆的离心率为e,则 ( )
A. B. C. D.
【答案】D
【分析】根据题意先求得短半轴长 ,再根据正弦定理求得 ,进而根据离心率的公式求解
即可
【详解】因伞柄底端正好位于该椭圆的长轴上,
由图可知,椭圆的短半轴长 ,
在 中, ,
由正弦定理得:
,
所以 ,故选:D.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.在棱长为2的正方体 中, 分别是棱 的中点,则( )
A. 与 是异面直线
B.存在点 ,使得 ,且 平面
C. 与平面 所成角的余弦值为
D.点 到平面 的距离为
【答案】BC
【分析】A选项,建立空间直角坐标系,根据 得到 与 平行;B选项,先求出 ,
得到平面 的法向量 ,根据数量积为0得到 ,得到 平面 ;C选项,先求
出 与平面 所成角的正弦值,进而求出余弦值;D选项,求出平面 的法向量,根据点到平面
距离公式求出答案.
【详解】A选项,以 作坐标原点, 所在直线分别为 轴,建立空间直角坐标系,
,
则 ,由于 ,故 与 平行,A错误;B选项,设 ,因为 ,所以 ,
即 ,解得 ,故 ,
设平面 的法向量为 ,
则 ,
令 ,则 ,则 ,
因为 ,故 , 平面 ,
故存在点 ,使得 ,且 平面 ,B正确;
C选项,平面 的法向量为 ,
故 与平面 所成角的正弦值为 ,
则 与平面 所成角的余弦值为 ,C正确;
D选项,设平面 的法向量为 ,
则 ,
令 ,则 ,故 ,
则点 到平面 的距离为 ,D错误.故选:BC
10.已知函数 ,则( )
A. B. 恰有5个零点
C. 必有极值点 D. 在 上单调递减
【答案】BCD
【分析】代入求值判断A,根据零点定义结合余弦函数方程根判断B,利用导数研究函数的极值点、单调
性判断CD.
【详解】对于A, ,错误;
对于B, ,
令 得 ,所以 或 ,又 ,
所以 或 或 或 或 ,
解得 或 或 或 或 ,即 恰有5个零点,正确;
对于C,因为 ,所以 ,因为 , ,
由零点存在性定理知 在 上存在异号零点,
则 在 必有极值点,正确;
对于D,当 时, , ,
所以 ,
当 时, , ,
所以 , ,所以 ,
所以 时,所以 ,所以 在 上单调递减,正确.
故选:BCD
11.已知 为坐标原点, 为抛物线 的焦点,过点 的直线交 于 、 两点,直线 、
分别交 于 、 ,则( )
A. 的准线方程为 B.
C. 的最小值为 D. 的最小值为
【答案】ABD
【分析】利用抛物线的方程求出准线方程,可判断A选项;设出直线 的方程,将该直线的方程与抛物
线的方程联立,结合韦达定理结合平面向量数量积的坐标运算可判断B选项;利用抛物线的焦半径以及基
本不等式可判断C选项;利用韦达定理结合基本不等式可判断D选项.
【详解】对于A选项,对于抛物线 , ,可得 ,
所以,抛物线 的准线方程为 ,A对;对于B选项,若直线 与 轴重合,此时,直线 与抛物线 只有一个公共点,不合乎题意,
设直线 的方程为 ,设点 、 ,
联立 ,可得 , ,
所以, , ,
则 ,则 ,B对;
对于C选项, ,
当且仅当 时,即当 时,等号成立,故 的最小值为 ,C错;
对于D选项,设点 、 ,
设直线 的方程为 ,联立 可得 ,
判别式为 ,由韦达定理可得 , ,同理可得 ,,同理可得, ,
所以,
,
当且仅当 时,即当 时,等号成立,
所以, 的最小值为 ,D对.
故选:ABD.
12.在平面直角坐标系xOy中,将函数 的图象绕坐标原点逆时针旋转 后,所得曲
线仍然是某个函数的图象,则称 为“ 旋转函数”,则( )
A.存在“90°旋转函数”
B.“70°旋转函数”一定是“80°旋转函数”
C.若 为“45°旋转函数”,则
D.若 为“45°旋转函数”,则
【答案】ACD
【分析】对A,举例说明即可;对B,举反例判断即可;根据函数的性质,结合“ 旋转函数”的定义逐
个判断即可;对CD,将 旋转函数转化为函数与任意斜率为1的函数最多一个交点,再联立函数与直线
的方程,分析零点个数判断即可.
【详解】对于A,如 ,旋转90°后为 满足条件,故A正确;
对于B,如倾斜角为 的直线是 旋转函数,不是 旋转函数,故B错误;
对与C,若 为 旋转函数,
则根据函数的性质可得, 逆时针旋转 后,不存在与 轴垂直的直线,使得直线与函数有1个以上的交点.
故不存在倾斜角为 的直线与 的函数图象有两个交点.
即 与 至多1个交点.
联立 ,可得 .
当 时, 最多1个解,满足题意;
当 时, 的判别式 ,
对任意的 ,都存在 使得判别式大于0,不满足题意,故 .故C正确;
对与D,同C, 与 的交点个数小于等于1,
即对任意的 , 至多1个解,故 为单调函数,
由 ,故 恒成立,即 恒成立.
即 图象在 上方,故 ,即 .
当 与 相切时,可设切点 ,
对 求导有 ,故 ,解得 ,此时 ,故 .故D正确.
故选:ACD.
【点睛】数学中的新定义题目解题策略:①仔细阅读,理解新定义的内涵;②根据新定义,对对应知识进
行再迁移.第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.已知 ,且 ,若 的展开式中存在常数项,则展开式中 的系数为 .
【答案】6
【分析】根据展开式通项公式及存在常数项确定 ,再求出展开式中含 的项即可得解.
【详解】 展开式的通项公式为 ,
因为存在常数项,所以 ,故只有当 时满足题意,
即求 展开式中含 的项的系数,
令 ,即 ,
所以展开式中含 的项为 ,
所以展开式中 的系数为6.
故答案为:6
14.已知圆 和两点 , .若圆 上存在点 ,使得
,则 的最大值为 .
【答案】11
【分析】首先判断点 在以 为直径的圆上(不能是 两点),将问题化为两圆有交点求参数范围,
即可得最大值.
【详解】由题意得:圆 的圆心 ,半径 ,
∵ ,则点 在以 为直径的圆上(不能是 两点),
以 为直径的圆的圆心为 ,半径 ,
注意到圆心 到y轴的距离为 ,即y轴与圆 相离,由题意得:圆 与圆 有公共点(由于y轴与圆 相离,公共点不可能为 ),且 ,
则 ,即 ,解得 ,故 的最大值为11.
故答案为:11
15.已知 是定义域为 的奇函数.若以点 为圆心,半径为2的圆在x轴上方的部分恰好是
图像的一部分,则 的解析式为 .
【答案】
【分析】求出给定圆的方程,再根据给定条件结合奇函数的定义求出 的解析式.
【详解】以点 为圆心,半径为2的圆的方程为 ,
则该圆在x轴上方的部分的方程为 ,
由 是奇函数,得 ,当 时, ,
,
所以 的解析式为 .故答案为:
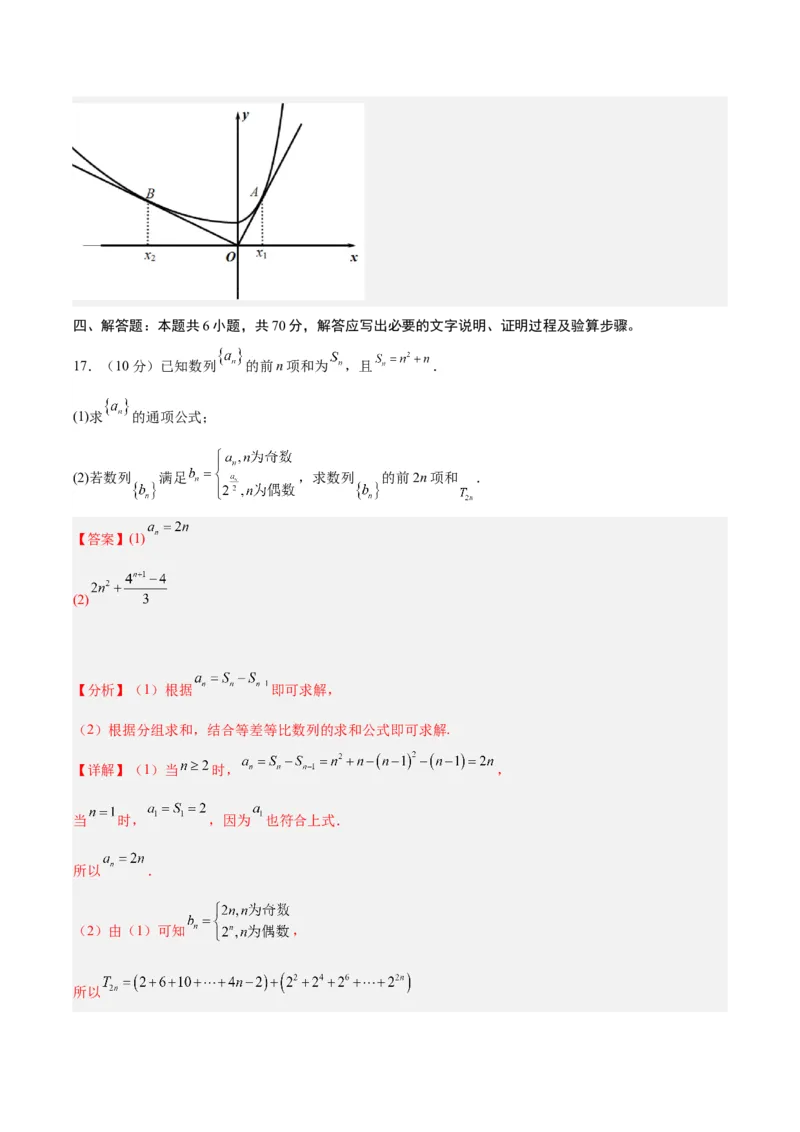
16.如图,对于曲线G所在平面内的点O,若存在以O为顶点的角 ,使得对于曲线G上的任意两个不同
的点 恒有 成立,则称角 为曲线G的相对于点O的“界角”,并称其中最小的“界角”为
曲线G的相对于点O的“确界角”.已知曲线C: (其中e是自然对数的底数),点O
为坐标原点,曲线C的相对于点O的“确界角”为 ,则 .
【答案】1
【分析】求过原点曲线的两条切线,求解两切线的夹角即可.
【详解】函数 ,
因为 ,
所以该函数在 单调递减,在 单调递增.
过原点作 的切线,设切点 ,
由 ,则切线 的斜率为 ,
直线 过 ,∴ ,∴ ,
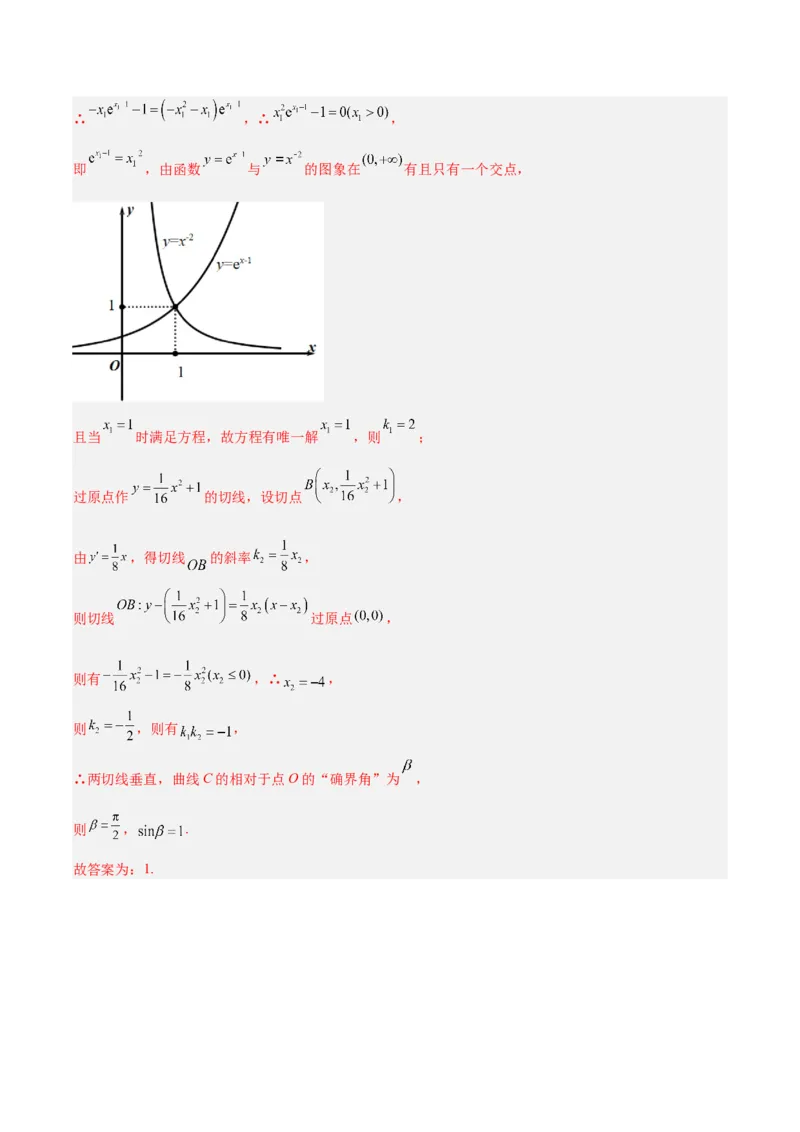
即 ,由函数 与 的图象在 有且只有一个交点,
且当 时满足方程,故方程有唯一解 ,则 ;
过原点作 的切线,设切点 ,
由 ,得切线 的斜率 ,
则切线 过原点 ,
则有 ,∴ ,
则 ,则有 ,
∴两切线垂直,曲线C的相对于点O的“确界角”为 ,
则 , .
故答案为:1.四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(10分)已知数列 的前n项和为 ,且 .
(1)求 的通项公式;
(2)若数列 满足 ,求数列 的前2n项和 .
【答案】(1)
(2)
【分析】(1)根据 即可求解,
(2)根据分组求和,结合等差等比数列的求和公式即可求解.
【详解】(1)当 时, ,
当 时, ,因为 也符合上式.
所以 .
(2)由(1)可知 ,
所以.
18.(12分)在 中,内角A,B,C的对边分别为a,b,c,且向量 ,
, .
(1)求角A的大小;
(2)若 为 上一点,且 , ,求 面积的最大值.
【答案】(1)
(2)
【分析】(1)根据向量垂直得到 ,计算化简得到 ,根据余弦定理得到答案.
(2)根据余弦定理得到 ,再利用均值不等式得到 ,计算面积得到最值.
【详解】(1) ,故 ,
即 ,故 ,
整理得到 ,即 , ,故 .
(2) , ,故 为等边三角形,即 ,
中: ,即 ,
即 ,当且仅当 时等号成立.
.
19.(12分)如图,已知四边形 和 都是直角梯形, , , , ,
, ,且二面角 的大小为 .
(1)证明:平面 平面 ;
(2)在线段 上是否存在点 ,使得二面角 的大小为 ,若存在,请求出点的位置;若不存
在,请说明理由.
【答案】(1)证明见解析
(2)存在点 ,使得二面角 的大小为 , .
【分析】(1)根据线面垂直的判定定理和面面垂直的判定定理进行证明即可;
(2)建立空间直角坐标系,利用二面角的定义,结合空间向量夹角公式进行求解即可.
【详解】(1)因为四边形 和 都是直角梯形,
所以 , ,且 平面 ,
所以, 平面 ,
因为 平面 ,所以平面 平面 .
(2)过点 、 分别作直线 、 的垂线 、 垂足为 、 .
由已知和平面几何知识易知, , ,
则四边形 和四边形 是矩形,所以在 和 中, ,
假设在 上存在点 ,使得二面角 的大小为 .
由(1)知 平面 ,则 是二面角 的平面角,
所以 ,所以 是正三角形.取 的中点 ,则 ,又 平面 ,
所以 平面 ,过点 作 平行线 ,
则以点 为原点, , 、 所在直线分别为 轴、 轴、 轴建立空间直角坐标系 ,
设 ,则 , , , ,
则 ,则 , ,
设平面 的法向量为 ,
由 ,得 ,取 ,
又平面 的法向量 ,所以 ,
整理化简的 ,解得 或 (舍去).
所以存在点 ,使得二面角 的大小为 ,且 .
20.(12分)已知 , .
(1)函数 有且仅有一个零点,求 的取值范围.
(2)当 时,证明: (其中 ),使得 .
【答案】(1)
(2)证明见解析【分析】(1)根据题意转化为方程 仅有一个实数根,设 ,求得 ,得到函
数的单调性和极值,作出函数的图象,结合图象,即可求解;
(2)设 ,转化为 在 存在极值点,求得 的值,即可求解.
【详解】(1)由函数 ,可得 ,所以 不是函数的零点,
因为函数 有且仅有一个零点,即方程 仅有一个实数根,
即方程 仅有一个实数根,即方程 仅有一个实数根,
设 ,可得 ,
当 时, , 单调递增;
当 时, , 单调递减;
当 时, , 单调递减,
所以函数 的极小值为 ,
又由当 且 时, ;当 且 时, ,
所以函数 的图象如图所示,
要使得函数 有且仅有一个零点,则满足 或 ,
即实数 的取值范围是 .(2)解:设 ,即 ,
当 ,令
满足 ,且 ,
若 在区间 单调递增,此时 ,不满足题意;
若 在区间 单调递减,此时 ,不满足题意;
所以函数 在区间 上不是单调函数,所以函数 在区间 上必有极值点,
即存在 ,使得 ,即 ,
即 ,使得 .
【点睛】方法总结:利用导数证明或判定不等式问题:
1、通常要构造新函数,利用导数研究函数的单调性与极值(最值),从而得出不等关系;
2、利用可分离变量,构造新函数,直接把问题转化为函数的最值问题,从而判定不等关系;
3、适当放缩构造法:根据已知条件适当放缩或利用常见放缩结论,从而判定不等关系;
4、构造“形似”函数,变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.
21.(12分)已知动点P到定点 的距离和它到直线 距离之比为2;
(1)求点P的轨迹C的方程;
(2)直线l在x轴上方与x轴平行,交曲线C于A,B两点,直线l交y轴于点D.设OD的中点为M,是否存
在定直线l,使得经过M的直线与C交于P,Q,与线段AB交于点N, , 均成立;若存在,求出l的方程;若不存在,请说明理由.
【答案】(1)
(2)存在,
【分析】(1)设 ,由 化简可求轨迹C的方程;
(2)设直线PQ的方程为 ,与双曲线联立得出韦达定理,结合两个向量共线的坐标表示
求得m,得到直线l的方程.
【详解】(1)设 ,由动点P到定点 的距离和它到直线 距离之比为2,
可得 ,化简得 ,即 ,
故点P的轨迹C的方程为 ;
(2)设l的方程为 ,则 ,故 ,
由已知直线PQ斜率存在,设直线PQ的方程为 ,故 .
与双曲线方程联立得: ,
由 对应渐近线方程为: ,易判断 ,
得 ,设 , ,
则 , ①,
由 , 得:,
,
即 , ,
消去 得: ,
即 ②
由①②得: ,化简得 ,由已知 ,
故存在定直线l: 满足条件.
22.(12分)某种植物感染病毒 极易死亡,当地生物研究所为此研发出了一种抗病毒 的制剂.现对20
株感染了病毒 的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果
进行统计,并对植株吸收制剂的量(单位:毫克)进行统计.规定植株吸收在6毫克及以上为“足量”,
否则为“不足量”.现对该20株植株样本进行统计,其中“植株存活”的13株,对制剂吸收量统计得下
表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
编号 1 2 3 4 5 6 7 8 9 10
吸收量(毫克) 6 8 3 8 9 5 6 6 2 7
1 1 1 1
编号 11 13 15 17 19 20
2 4 6 8
吸收量(毫克) 7 5 10 6 7 8 8 4 6 9
(1)补全列联表中的空缺部分,依据 的独立性检验,能否认为“植株的存活”与“制剂吸收足量”有关?
吸收足
吸收不足量 合计
量
植株存活 1
植株死亡
合计 20
(2)现假设该植物感染病毒 后的存活日数为随机变量 ( 可取任意正整数).研究人员统计大量数据
后发现:对于任意的 ,存活日数为 的样本在存活日数超过 的样本里的数量占比与存活日数
为1的样本在全体样本中的数量占比相同,均等于0.1,这种现象被称为“几何分布的无记忆性”.试推导
的表达式,并求该植物感染病毒 后存活日数的期望 的值.
附: ,其中 ;当 足够大时, .
0.010 0.005 0.001
6.635 7.879 10.828
【答案】(1)表格见解析,可以认为 成立,即认为“植株的存活”与“制剂吸收足量”无关.
(2) , .
【分析】(1)根据独立性检验先求出 ,再将 与对应 比较大小即可.
(2)先根据递推关系得到 与 的关系,进而利用等比数列得到通项公式,推导出
的表达式,最后得到 的表达式,应用错位相减法求和即可.
【详解】(1)填写列联表如下:
吸收足
吸收不足量 合计
量植株存活 12 1 13
植株死亡 3 4 7
合计 15 5 20
零假设为 :“植株的存活”与“制剂吸收足量”无关联.
根据列联表中的数据,经计算得到: ,
依据 的独立性检验,没有充分证据推断 不成立,因此可以认为 成立,即认为“植株的存
活”与“制剂吸收足量”无关.
(2)由题意得 .
又 ,故 .
把 换成 ,则 .
两式相减,得 ,
即 .
又 ,
故 对任意 都成立,
从而 是首项为0.1,公比为0.9的等比数列,因此 .
由定义可知 ,
而 ,下面先求 .
,
,
作差得.
所以 ,当 足够大时, , ,故
,可认为 .