文档内容
广州市真光中学 2025 届高三开学质量检测
数学
2024.08
本试卷共 5 页,19 小题,满分 150 分.考试用时 120 分钟.
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上.用 2B 铅笔在答
题卡的相应位置填涂考生号.
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑:
如需改动,用橡皮擦干净后,再选涂其他答案.答案不能在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相
应位置上:如需改动,先划掉原来的答案,然后再写上新答案:不准使用铅笔和涂改液.不按以上
要求作答无效.
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、选择题:本题共 8 小题,每小题 5 分,共 40 分,在每小题给出的四个选项中,只有
一 项、是符合题目要求的.
{ 2 }
1. 已知集合A = {−1, 0,1, 2} , B = x | x < 2 ,则A ∩ B =
A. {0,1} B. {−1,1} C. {−1, 0,1} D. {0,1, 2}
【答案】C
【解析】
【分析】
根据一元二次不等式解法求得集合B ,由交集定义得到结果.
, : A ∩ B =
故选: C .
【点睛】本题考查集合运算中的交集运算,涉及到一元二次不等式的求解,属于基础题.
2. 已知复数z 满足(1+ i)z = i3 (i 为虚数单位),则 z = ( )
A. − B. − − C. D. − +
【答案】B
第1页/共25页【解析】
【分析】根据复数代数形式的除法运算化简即可.
【详解】因为(1+ i)z = i3 ,
故选:B
→
3. 已知向量 = (1, λ) , b = (2, −1) .若 ( + 2 ) 丄 ,则 λ= ( )
A. 1 B. −1 C. 12 D. −12
【答案】C
【解析】
【分析】(方法一)由 , 的坐标,求得 + 2 的坐标,利用向量垂直的坐标表示式列出方程求解即得;
( )
(方 法二)先由 + 2 丄 化简,再代入 , 得坐标计算即得.
【详解】(方法一)由 = (1, λ) , = (2, −1) ,得 + 2 = (5, λ− 2) .
由 ( + 2 ) 丄 ,得 ( + 2 ) . = 0 ,即5× 2 +(λ− 2)× (−1) = 0 ,解得λ= 12 .
故选:C .
(方法二)由 ( + 2 ) 丄 ,得 ( + 2 ) . = 0 ,即 . + 2 2 = 0 ,
将 = (1, λ), = (2, −1) 代入得,1 × 2 +λ× (−1) + 2× 22 + (−1) 2 = 0 ,解得λ= 12 .
故选:C .
4. 已知2cos(2α +β)− 3cosβ= 0 ,则tanαtan(α + β) = ( )
1 1
A. 5 B. C. -5 D. −
5 5
【答案】D
【解析】
【分析】由角的变换2α +β= α + (α + β), β= (α + β)−α , 利用余弦的和,差角公式和展开,从而
可得 答案.
【详解】 2cos (2α +β) = 3cosβ,则2cos(α + β+α) = 3cos (α + β−α)
则2cosαcos(α + β)− 2sin(α + β)sinα = 3cos (α + β)cosα + 3sin (α + β)sinα, ,
第2页/共25页即−5sin(α + β)sinα = cos (α + β)cosα , 所以−5tan(α + β)tanα = 1 ,
故选:D
x 0
5. 已知函数 (a > 0 且a ≠ 1) 在R 上单调递减,则a 的取值范围为
x 0
( )
B. C. D.
【答案】A
【解析】
【分析】由函数f(x) 在R 上单调递减,结合分段函数的单调性的概念,得到不等式组 即
可
3a ≥ log 1
a
l
求解.
x 0
【详解】由题意,函数f (a > 0 且a ≠ 1) 在R 上单调递减,
x 0
则满足 解得 即实数a 的取值范围为 .
故选:A .
【点睛】本题主要考查了利用分段函数的单调性求解参数问题,其中解答中熟记分段函数的单调性的概
念,结合二次函数的性质和对数的运算,列出相应的不等式组是解答的关键,着重考查了推理与运算能
力,属于基础题.
6. 已知某圆柱的底面直径与某圆锥的底面半径相等,且它们的表面积也相等,圆锥的底面积是圆锥侧面积
的一半,则此圆锥与圆柱的体积之比为( )
A. 8: 5 3 B. 4 :5 3 C. 2 3 :5 D. 4 :11 3
第3页/共25页【答案】A
第3页/共25页【解析】
【分析】
首先设出圆锥的底面半径r 和母线长l ,根据圆锥的底面积是圆锥侧面积的一半,求得 l = 2r .利用勾股定
理 求得圆锥的高h ,由此求得圆锥的体积V 根据题意求得圆柱的底面半径,根据圆锥与圆柱的表面积相
1
1.
等, 求得圆柱的高h ,由此求得圆柱的体积.从而求得圆锥与圆柱的体积之比.
2
【详解】设圆锥的底面半径为r ,母线长为l ,则 πr2 = × 2πr . l ,即l = 2 r ,所以圆锥的高
3
, 圆锥的体积 πr2 h = πr3 . 由题意,知圆柱的底面半径为 ,设圆柱的高为h ,因
1 2
为圆锥与圆柱的表
2 2
面积相 等 ,所 以 3πr2 = 2π + 2π 解得 所 以 圆柱 的体 V = π h =
2 2
πr2 , 故
故选:A
【点睛】本题考查简单几何体的表面积与体积,考查空间想象能力.
( ) ( )
7. 函数y = 与y = 3sin 的图像有n 个交点,其坐标依次为 x , y , x , y , ⅆ ,
1 1 2 2
)
, 则
A. 4 B. 8
C. 12 D. 16
【答案】A
【解析】
【分析】由已知函数解析式可知两个函数对称中心均为为(0,1) ,在同一坐标系中作出两个函数的图象,
结 合图象根据对称性即可得到答案.
+1 ,y = 3sin 两个函数对称中心均为为(0,1) ,在同一坐标系中作
出
两个函数的图象,如图:
第4页/共25页由图可知共有四个交点,且关于 对称,故 .
故选:A.
【点睛】本题主要考查函数的图象,中心对称图形的特点,属于中档题.
8. 定义在R 上的 函数f (x) 满足f (0) = 0 , f (x) + f (1− x) = 1 , ,且当0 ≤ x <
1
x ≤ 1 时
2
A. B. C. D.
【答案】D
【解析】
【分析】先由已知条件求出一些特值 = 1,f 反复利用 可得
( )
, 再由 与 、f | 与 的大小关系从而得出结论.
|(
,
【详解】: f (0) = 0 ,f (x) + f (1− x) = 1 ,
令x = 1得:f = 1 ,又f ⇒ f
反复利用 可得:
第5页/共25页再令 可求得 ,
第5页/共25页同理反复利用 可得:
由①②可得:有f
0 ≤ x < x ≤ 1 ,f ,而0 <
1 2
, 所以f ( ) ≥ f ( ) = ,
1 1
故
故选:D .
二、选择题:本题共 3 小题,每小题 6 分,共 18 分,在每小题给出的选项中,有多项符合
题 目要求,全部选对的得 6 分,部分选对的得部分分,有选错的得 0 分
9. 李明每天 7 :00 从家里出发去学校,有时坐公交车,有时骑自行车.他各记录了 50 次坐公交车和骑
自 行车所花的时间,经数据分析得到:坐公交车平均用时 30 分钟,样本方差为 36;自行车平均用时
34 分 钟,样本方差为 4 .假设坐公交车用时X 和骑自行车用时 Y 都服从正态分布,则( )
A. P(X>32)>P(Y>32)
B. P(X≤36)=P(Y≤36)
C. 李明计划 7 :34 前到校,应选择坐公交车
D. 李明计划 7 :40 前到校,应选择骑自行
车 【答案】BCD
【解析】
【分析】首先利用正态分布,确定μ 和σ ,再结合正态分布的对称性,和3σ的原则,即可求解.
【详解】A.由条件可知X □ N ( 30, 62 ) ,Y ~ N ( 34, 22 ) ,根据对称性可知P(Y > 32) > 0.5 > P(X >
32) ,
故 A 错误;
B. P (X ≤ 36) = P (X ≤ μ + σ) , P (Y ≤ 36) = P (Y ≤ μ + σ),所以P(X ≤ 36) = P (Y ≤ 36) ,
故 B 正确;
C. P (X ≤ 34) > 0.5= P (Y ≤ 34) ,所以P(X ≤ 34) > P(Y ≤ 34) ,故 C 正确;
D. P (X ≤ 40) < P(X < 42) = P (X < μ + 2σ) , P (Y ≤ 40) = P (Y ≤ μ + 3σ) ,
所 以
P (X ≤ 40) < P(Y ≤ 40),故 D 正
第6页/共25页确. 故选:BCD
第6页/共25页10. 已知f (x)是定义在R 上的奇函数,当x ∈(0, +∞ ) 时,f (x) = x3 − 3x − 2 ,则( )
A. f (x) 的极大值点为−1
B. 函数y = f 的零点个数为
3 C. 函数y = f (f (x)) 的零点个数为
7
D. f (f (x)) > 0 的解集为(−2, 0)u (2, +∞ )
【答案】ABC
【解析】
【分析】利用导函数求出单调区间,根据极值定义和奇偶性可判断 A;数形结合判断 B 、C;赋值方法判
断 D
【详解】由题意得f (0) = 0 ,
当x ∈(0, +∞) 时,f (x) = x3 − 3x − 2 ,得 f ′ (x) = 3x2 − 3 ,
令f ′ (x) > 0 ,得 x >1 ,
令f ′ (x) < 0 ,得 0 < x < 1;
所以f (x)在(0,1) 单调递减,在 (1, +∞) 单调递增,
所以f (x) 的极小值点为 1 ,
又是定义在R 上的奇函数,所以f (x) 的极大值点为−1,故 A
对; 当x < 0 时,则 −x > 0 ,所以 f (−x) = −x3 + 3x − 2 ,
又f (x)是定义在R 上的奇函数,所以f (−x) = −f (x),所以 f (x) = x3 − 3x + 2
分别画出 和 的图象,
第7页/共25页得函数 的零点个数为 3 ,B对;
令f (x) = 0 ,得 x = 0 或x= − 1或x = 2 ,
令f (f (x )) = 0 ,得 f (x) = 0 ,或 f (x) =
±2 , 如图,分别画出y = f (x), y = −2, y = 2
的图象,
由图可知:函数y = f ( f (x )) 的零点个数为 7 , C 对;
故 D 错;
故选:ABC
【点睛】方法点睛:
对于零点个数的求法:一是通过解方程求出零点,二是数形结合法:先对解析式变形,进而构造两个函
数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解
11. 天文学家卡西尼在研究土星及其卫星的运行规律时,发现了平面内到两个定点的距离之积为常数的点的
轨迹.我们称其为卡西尼卵形线(CassinniOcal ). 在平面直角坐标系中,设定点为F (−2, 0), F (2, 0),
1 2
点O 为坐标原点,动点P(x, y) 满足 PF . PF = 4 .下列四个命题中,正确的是 ( )
1 2
A. 点 P 的轨迹既是中心对称又是轴对称图形 B. 点P 的横坐标的取值范围是[−4, 4]
C. PF + PF 的最小值为4 D. △F PF 的面积的最大值为2
1 2 1 2
【答案】ACD
【解析】
【分析】A 项根据轴对称图形、中心对称图形的方程特征进行判断即可;B 项结合曲线方程特征消元转化
进
第8页/共25页行判断即可;C 项根据卡西尼卵形线的定义,结合基本不等式进行判断即可;D 项根据方程特征求得 P 纵
坐 标的范围,结合三角形面积公式进行判断即可.
【详解】由题意可知 P 的轨迹方程为 2 +y2 . 2 +y2 = 4 ,
则P(x, y) 关于x 轴对称的点P (x, −y ) 的横纵坐标满足
1
同理P(x, y) 关于y 轴对称的点P (−x, y) ,
2
关于原点对称的点P (−x, −y ) 均满足轨迹方程
3
J(
−x + 2
)2
+
(
− y
)2
. = . = 4
, 即 P 的轨迹关于x 轴、y 轴轴对称,关于原点中心对称,故 A 正确;
由基本不等式可知 = 4 ,当且仅当
即P(0, 0) 时取得最小值,故 C 正确;
将轨迹方程 2 +y2 . 2 +y2 = 4平方得
( )2 ( ) ( )2
x2 − 4 + y4 + 2y2 x2 + 4 = 16 ⇒ x2 + y2 + 4 = 16 +16x2
2
整理得y2 = 4 x2+1 − x2 − 4 = − +1≥ 0
, 解之得 · ∈ [ 1,3 ] ,
所以1≤ x2 +1≤ 9 ⇒ x ∈ −2 , 2 ,故 B 错误;
2
又因为y2 = − +1≤ 1 ,故 ≤ 1 ⇒ S
□
当且仅当x2 = 3, y2 = 1时取得最大值,故 D 正
确. 故选:ACD.
【点睛】难点在于对轨迹方程的变形与化简,利用方程的特点求横纵坐标的取值范围是本题关键.
三、填空题:本题共 3 小题,每小题 5 分,共 15 分
2 2
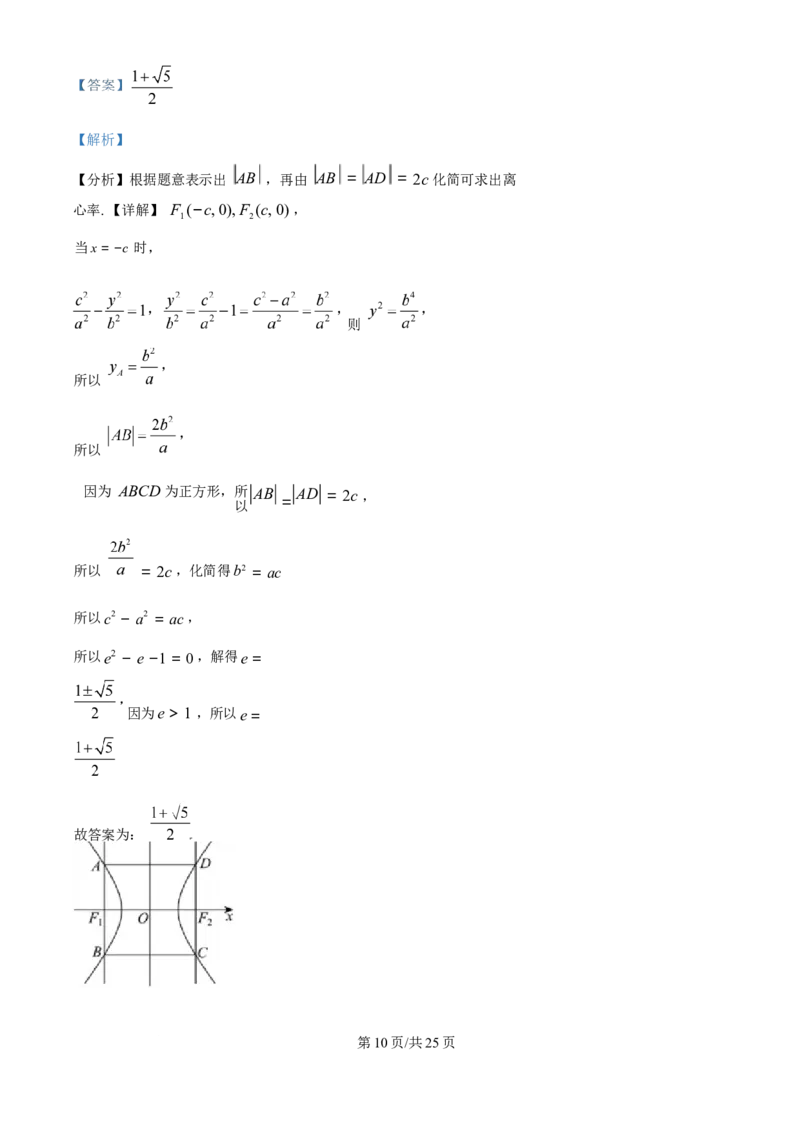
12. 双曲线 = 1 ,过左、右焦点作平行于y 轴的直线交双曲线于A ,B ,C,D,若 ABCD 构成
正方
第9页/共25页形,求双曲线的离心率为 .
第9页/共25页【解析】
【分析】根据题意表示出 AB ,再由 AB = AD = 2c 化简可求出离
心率. 【详解】 F (−c, 0), F (c, 0) ,
1 2
当x = −c 时,
则
所以
所以
因为 ABCD 为正方形,所 AB AD = 2c ,
以 =
所以 = 2c ,化简得b2 = ac
所以c2 − a2 = ac ,
所以e2 − e −1 = 0 ,解得e =
因为e > 1 ,所以e =
故答案为:
第10页/共25页13. 已知曲线C :f (x) = ex + a 和曲线C :g (x) = ln (x + b) + a2 (a, b ∈ R) ,若存在斜率为 1
1 2
的直线与
C , C 同时相切,则 b 的取值范围是 .
1 2
第10页/共25页【解析】
【分析】分别求出两函数的导函数,再分别设直线与两曲线的切点的横坐标,由于斜率为 1 即导数值为
1 分别求出切点横坐标,可得切线方程,再根据切线方程系数相等得与的关系式,再根据二次函数性质可
求 出 b 的取值范围.
【详解】由题意得 = ex , g ′
设斜率为 1 的切线在C , C 上的切点横坐标分别为x ,x ,
1 2 1 2
所以ex 1 = = 1 ,则x = 0 ,x = 1− b ,
1 2
两点处的切线方程分别为y− (1+ a ) = x ,y − a2 = x − (1− b) ,
所以a +1 = a2 −1+ b ,即b = 2 + a − a 2 = −
所以 b 的取值范围为
. 故答案为 .
14. 编号为 1 、2、3、4 的四名学生随机入座编号为 1 、2 、3 、4 的座位,每个座位坐 1 人,座位编号和
学
生编号一致时称为一个“配对”,用 X 表示“配对”数,则 X 的期望E(X ) = .
【答案】1
【解析】
【分析】根据X 的可能取值,运用计数原理和古典概型逐项分析计算即可.
4
【详解】X 的可能取值为 0,1,2,4,全排列为A = 24 ,
4
当X=0 时,先安排的第一人由3 种选择,比如说先安排“1”号人,可以选择 2,3,4 座
位, 如果安排在 2 号位,则“2 ”号人也可以由 3 种选择,比如是安排在 1 号位,
则“3 ”号人只能在 4 号位,“4”号人只能在 3 号位;如果是安排在 3 号位,
则“3 ”号人只能在 4 号位,“4”号人只能在 1 号位,如果安排在 4 号位也是类似,
所以有3× 3 = 9 种排法
第11页/共25页1
当X=1 时,先从 4 人中选一人安排在对应的位置上,由C = 4 种选法,
4
比如选“1”号人安排在 1 号位,则“2 ”号人有 2 种选法,如果选 3,则“3”号人只能选
4, “4”号人只能 2,;如果选 4,则“4”号人只能只能选 3 ,“3”号人只能选 2;所以有
4× 2 = 8
种排法
2
当X=2 时,先从 4 人中选 2 人安排在对应的位置,有 C = 6 种选法,比如先安排“1”号人
4
和“2”号人,分别安排在 1 号和 2 号位置,则“3”号人和“4”号人只能由 1 种排法,所以总共
有 6 种排法 ;
当X=4 时,只有 1 种排法 ;
其数学期望为
故答案为:1.
四、解答题:本题共 5 小题,共 77 分.解答应写出文字说明、证明过程或演算步骤.
15. 在 □ABC 中,角 A, B, C 所对的边分别为a, b, c ,已知 cosB = ,b = 5,
(1)求a ;
(2)求sinA ;
(3)求cos (B − 2A) 的值.
【答案】(1)4
(2)
(3)
【解析】
【分析】(1)a = 2t, c = 3t ,利用余弦定理即可得到方程,解出即可;
(2)法一:求出sin B ,再利用正弦定理即可;法二:利用余弦定理求出cos A ,则得到sin A ;
(3)法一:根据大边对大角确定A 为锐角,则得到cos A ,再利用二倍角公式和两角差的余弦公式即
可; 法二:直接利用二倍角公式和两角差的余弦公式即可.
【小问 1 详解】
第12页/共25页设 a = 2t, c = 3t ,t > 0 ,则根据余弦定理得b2 = a2 + c2 − 2ac cosB ,
第12页/共25页即 25 = 4t2 + 9t2 − 2× 2t × 3t × , 解得t = 2
则a = 4, c = 6
. 【小问 2 详
解】
法一:因为B 为三角形内角,所以sin B = 1−cos2B =
4 5
a b = 7
再根据正弦定理 s 得 in A s in = B , 即 s i n A 5 7 , 解 得 s i n A 4 =
16
法二:由余弦定理得cos A =
因为A∈ (0, τ ) ,则 sin A = 1 − (| ) | 2 =
( ,
【小问 3 详解】
( )
法一:因为cosB = > 0 ,且B ∈ 0, τ ,所以
2
)
因为a < b ,则 A < B ,所以 cos A = 1 − = ,
|
,
3 3 3 ) 2 1
则sin 2A = 2sin A cos A = 2 × × = ,cos 2A = 2 cos2 A −1 = 2 × (| | −1 =
4 4 8 ( 4 ,
cos (B − 2A) = cos B cos 2A + sin B sin 2A = × + × = .
法二:sin 2A = 2sin A cos A = 2 ×
第13页/共25页2
( )
因为B 为三角形内角,所以sin B = = 1 − = ,
|
(|
,
第13页/共25页所以cos (B − 2A) = cos B cos 2A + sin B sin 2A =
16. 已知椭圆 以椭圆E 的焦点和短轴端点为顶点的四边形是边长为 2 的
( )
正 方形过点 ( 0, t ) t > 且斜率存在的直线与椭圆E 交于不同的两点 A B ,过点 A 和C ( 0,1 ) 的
. ,
直线 AC
与椭圆E 的另一个交点为D .
(1)求椭圆E 的方程及离心率;
(2)若直线 BD 的斜率为 0,求 t 的值.
= 1, e =
(2)t = 2
【解析】
【分析】(1)由题意得b = c = 2 ,进一步得a ,由此即可得解;
设AB : y = kx + t, 联立椭圆方程,由韦达定理
有 x + x = , x x = ,而AD : y = + y ,令x = 0 ,即可
1
1 2 1 2
得解.
【小问 1 详解】
由题意b = c = 从而 b2 +c2
=
2 , 所以椭圆方程为 离心率为
;
【小问 2 详解】
直线 AB 斜率不为 0,否则直线 AB 与椭圆无交点,矛盾,
第14页/共25页从而设 AB : y = kx + t,
第14页/共25页联立 化简并整理得 (1+ 2k2 )x2 + 4ktx + 2t2 − 4 = 0 ,
由题意△ = 16k2t2 −8 ( 2k2 +1 )( t2 − 2 ) = 8 ( 4k2 + 2 − t2 ) > 0 ,即k, t 应满足4k2 + 2 − t2 > 0 ,
所以x + x = , x x =
1 2 1 2
若直线BD斜率为 0,由椭圆的对称性可设D(−x , y ) ,
2 2
所以AD : y = + y ,在直线 AD 方程中令x = 0 ,
1
所以t = 2 ,
2 − t2 = 4k2 − 2 > 0
此时k 应满足 应满足k < − 或k > ,
- l2
综上所述,t = 2满足题意,此时k < − 或k > .
2 2
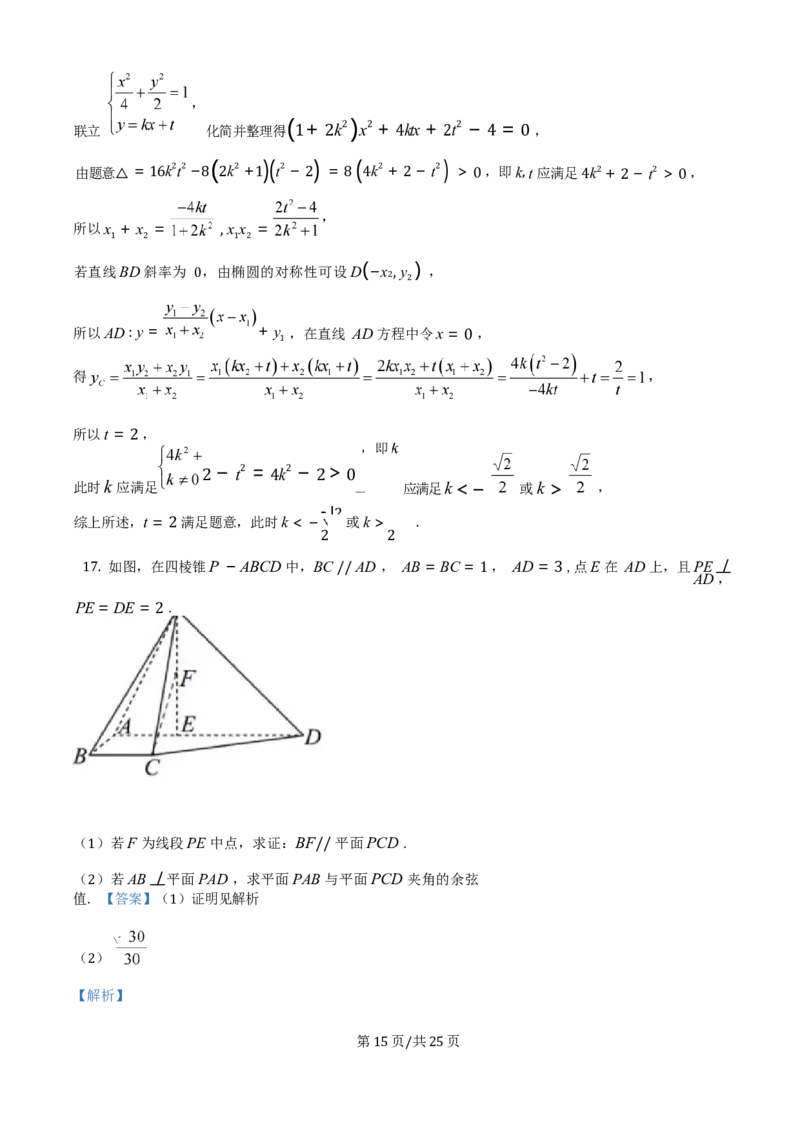
17. 如图,在四棱锥P − ABCD 中,BC // AD , AB = BC = 1 , AD = 3 ,点E 在 AD 上,且PE 丄
AD ,
PE = DE = 2 .
(1)若F 为线段PE 中点,求证:BF// 平面PCD .
(2)若AB 丄平面PAD ,求平面PAB 与平面PCD 夹角的余弦
值. 【答案】(1)证明见解析
(2)
【解析】
第15页/共25页【分析】(1)取 PD 的中点为S ,接SF, SC ,可证四边形SFBC 为平行四边形,由线面平行的判定定
理可 得BF// 平面PCD .
(2)建立如图所示的空间直角坐标系,求出平面APB 和平面PCD 的法向量后可求夹角的余弦
值. 【小问 1 详解】
取PD 的中点为S ,接SF, SC ,则SF//ED, SF = ED = 1,
而ED//BC, ED = 2BC ,故SF//BC, SF = BC ,故四边形SFBC 为平行四边形,
故BF//SC ,而 BF 丈平面PCD ,SC ⊂平面PCD
, 所以BF// 平面PCD .
【小问 2 详解】
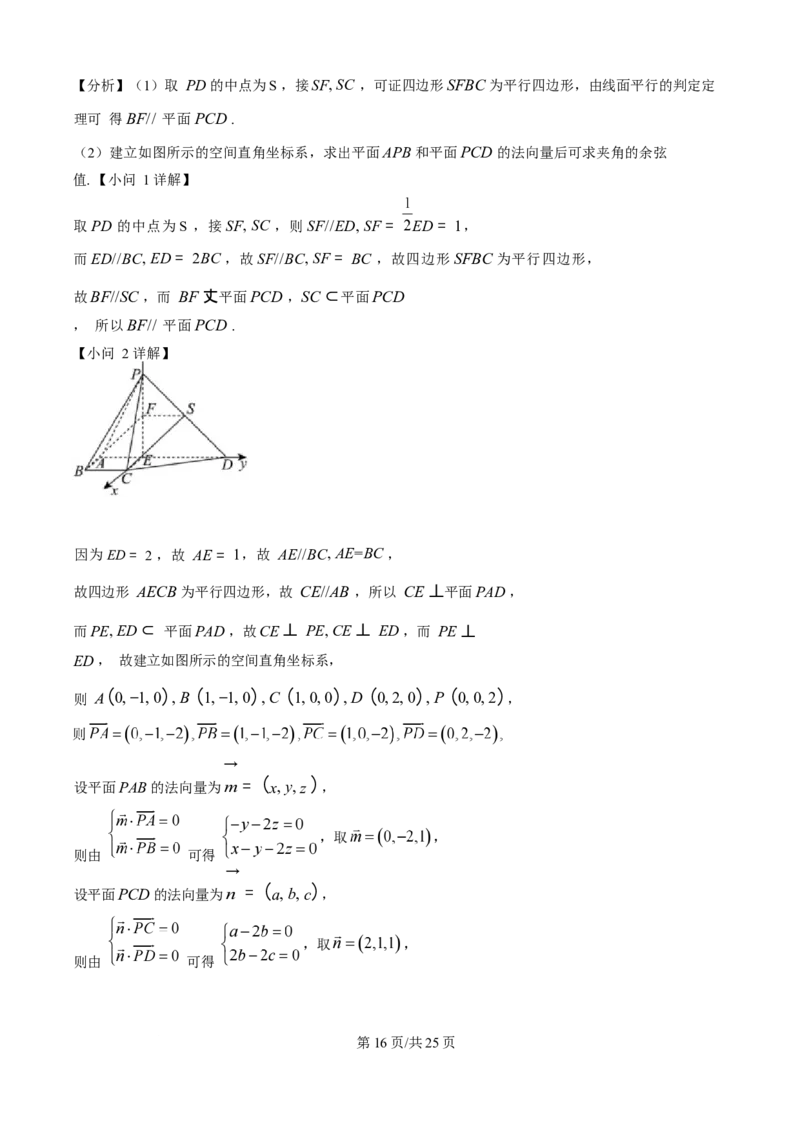
因为ED = 2 ,故 AE = 1,故 AE//BC, AE=BC ,
故四边形 AECB 为平行四边形,故 CE//AB ,所以 CE 丄平面PAD ,
而PE, ED ⊂ 平面PAD ,故CE 丄 PE, CE 丄 ED ,而 PE 丄
ED , 故建立如图所示的空间直角坐标系,
则 A (0, −1, 0), B (1, −1, 0), C (1, 0, 0), D (0, 2, 0), P (0, 0, 2) ,
→
设平面PAB的法向量为m = ( x, y, z ) ,
则由 可得
→
设平面PCD 的法向量为n = ( a, b, c ) ,
则由 可得
第16页/共25页故平面PAB与平面PCD 夹角的余弦值为
18. 设函数f (x) = x + kln(1+ x)(k ≠ 0) ,直线l 是曲线y = f (x)在点(t, f (t ))(t > 0) 处的切线.
(1)当k = − 1时,求f (x) 的单调区间.
(2)求证:l 不经过点(0, 0) .
(3)当k = 1 时,设点 A ( t, f (t ))(t > 0) , C (0, f (t )) , O (0, 0) ,B 为l 与y 轴的交点, S
□ ACO
与S 分别表示△ACO 与 □ ABO 的面积.是否存在点A 使得2S = 15S 成立?若存在,这
□ ABO △ACO △ABO
样的点A 有
几个?
(参考数据:1.09 < ln3 <1.10 ,1.60 < ln5 <1.61 ,1.94 < ln7 <1.95
) 【答案】(1)单调递减区间为(−1, 0) ,单调递增区间为(0,+∞) .
(2)证明见解析 (3)2
【解析】
【分析】(1)直接代入k = − 1 ,再利用导数研究其单调性即可;
(2)写出切线方程 ,将 代入再设新函数
利
用导数研究其零点即可;
(3 ) 分 别 写 出面积表达 式 ,代入 2S = 15S 得 到 13ln − 2t −15 再 设
□ ACO ABO
新 函数 = 13ln − 2t − 研究其零点即可.
【小问 1 详解】
当x ∈(−1, 0) 时,f ′ (x) < 0 ;当 x ∈(0, +∞) ,f ′ (x) > 0 ;
:f (x) 在(−1, 0) 上单调递减,在(0,+∞) 上单调递增.
则f (x) 的单调递减区间为(−1, 0) ,单调递增区间为(0,+∞)
. 【小问 2 详解】
第17页/共25页( k )
则切线方程为y − f (t) = | 1 + |(x −t)(t > 0) ,
( 1+ t,
( k ) ( k )
将(0, 0) 代入则−f (t) = −t | 1( + 1 + t,| , f ( t ) = t (| 1 + 1 + , t, |
即
令
假设l 过(0, 0) ,则F(t) 在t ∈(0, +∞) 存在零点.
> 0 , :F 在 上单调递增,F(t) > F(0) = 0 ,
:F (t) 在(0,+∞) 无零点,:与假设矛盾,故直线l 不过(0, 0)
. 【小问 3 详解】
S = tf (t) ,设l 与y 轴交点B 为(0, q) ,
O ACO
t > 0 时,若q < 0 ,则此时l 与f(x) 必有交点,与切线定义矛盾.
由(2)知q ≠ 0 .所以q > 0 ,
)
则切线l 的方程为y −t − ln ( t +1 ) = (| 1+ | (x −t) ,
( ,
t
令x = 0 ,则 y = q = y = ln(1+ t) − .
t +1
2S = 15S ,则2tf (t) = 15t ln(1 + t) − ,
O ACO ABO
:13ln(1+ t) − 2t −15 = 0 ,记 h(t) = 13ln(1+ t) − 2t − (t > 0) ,
:满足条件的 A 有几个即h(t) 有几个零点.
第18页/共25页)
当t ∈ (| 0,
|
时,h′ (t ) < 0 ,此时h(t ) 单调递减;
( ,
第18页/共25页当 时,h′ > 0 ,此时h 单调递增;
当t ∈(4, +∞) 时,h′ (t ) < 0 ,此时h(t ) 单调递减;
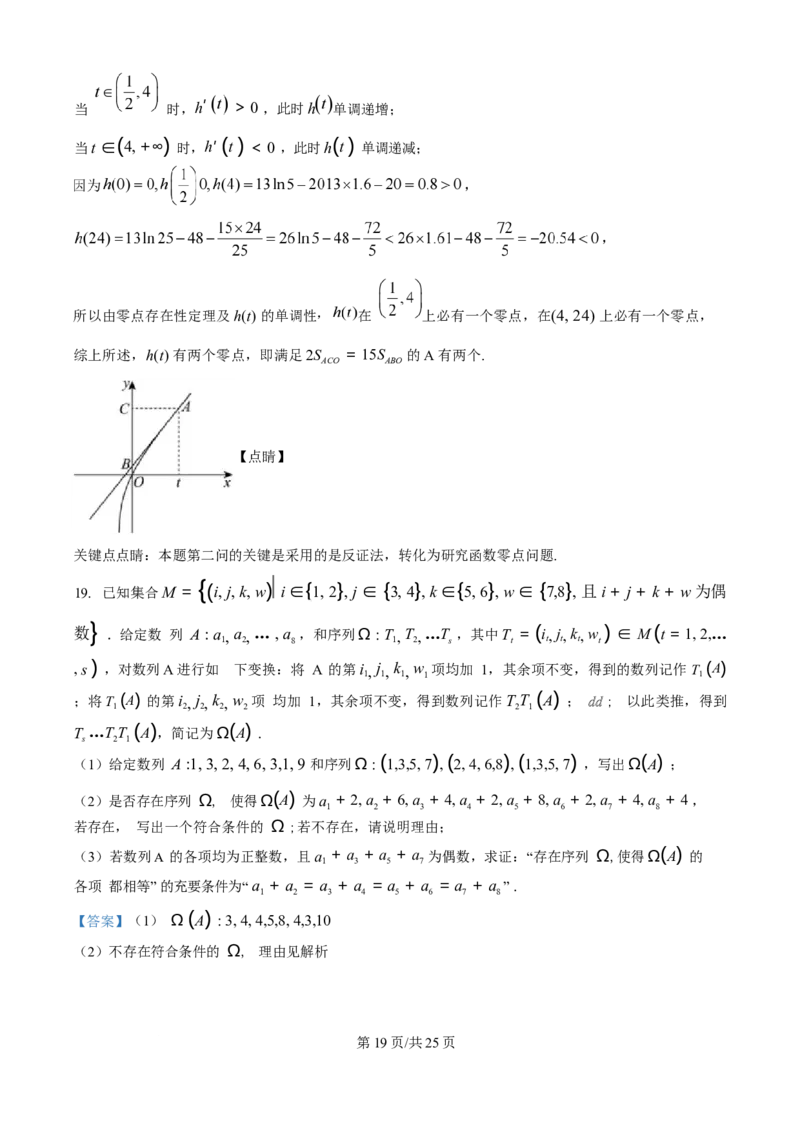
所以由零点存在性定理及h(t) 的单调性 在 上必有一个零点,在(4, 24) 上必有一个零点,
综上所述,h(t) 有两个零点,即满足2S = 15S 的A 有两个.
ACO ABO
【点睛】
关键点点睛:本题第二问的关键是采用的是反证法,转化为研究函数零点问题.
19. 已知集合M = { (i, j, k, w) i ∈ { 1 , 2}, j ∈ {3, 4}, k ∈{5, 6}, w ∈ {7,8}, 且i + j + k + w为偶
数} .给定数 列 A : a , a , … , a ,和序列Ω : T , T , …T ,其中T = (i, j, k, w ) ∈ M (t = 1, 2,…
1 2 8 1 2 s t t t t t
, s ) ,对数列A 进行如 下变换:将 A 的第i , j , k , w 项均加 1,其余项不变,得到的数列记作T (A)
1 1 1 1 1
;将T (A) 的第i , j , k , w 项 均加 1,其余项不变,得到数列记作T T (A) ; ⅆⅆ ; 以此类推,得到
1 2 2 2 2 2 1
T …T T (A),简记为Ω(A) .
s 2 1
(1)给定数列 A :1, 3, 2, 4, 6, 3,1, 9 和序列Ω : (1,3,5, 7), (2, 4, 6,8), (1,3,5, 7) ,写出Ω(A) ;
(2)是否存在序列 Ω, 使得Ω(A) 为a + 2, a + 6, a + 4, a + 2, a + 8, a + 2, a + 4, a + 4 ,
1 2 3 4 5 6 7 8
若存在, 写出一个符合条件的 Ω ;若不存在,请说明理由;
(3)若数列A 的各项均为正整数,且a + a + a + a 为偶数,求证:“存在序列 Ω,使得Ω(A) 的
1 3 5 7
各项 都相等” 的充要条件为“ a + a = a + a = a + a = a + a ” .
1 2 3 4 5 6 7 8
【答案】(1) Ω (A) : 3, 4, 4,5,8, 4,3,10
(2)不存在符合条件的 Ω, 理由见解析
第19页/共25页(3)证明见解析
【解析】
【分析】(1)直接按照Ω(A) 的定义写出Ω(A) 即可;
(2)解法一:利用反证法,假设存在符合条件的 Ω,由此列出方程组,进一步说明方程组无解即可;
解 法二:对于任意序列,所得数列之和比原数列之和多 4,可知序列 Ω共有 8 项,可知:
(b + b )− (a + a ) = 8, n = 1,2, 3,4 ,检验即可;
2n−1 2n 2n−1 2n
(3)解法一:分充分性和必要性两方面论证;解法二:若a + a = a + a = a + a = a + a ,分类
1 2 3 4 5 6 7 8
讨论 a , a , a , a 相等得个数,结合题意证明即可;若存在序列 Ω, 使得Ω(A) 为常数列,结合定义
1 3 5 7
分析证明 即可.
【小问 1 详解】
因为数列 A :1,3, 2, 4, 6, 3,1, 9 ,
由序列T (1,3,5, 7) 可得T (A) : 2,3,3, 4, 7,3, 2,9 ;
1 1
由序列T (2, 4, 6,8) 可得T T (A) : 2, 4,3,5, 7, 4,
2 2 1
2,10 ; 由序列T (1,3,5, 7) 可得T T T (A) : 3, 4,
3 3 2 1
4,5,8, 4,3,10 ; 所以Ω(A) : 3, 4, 4,5,8, 4,3,10 .
【小问 2 详解】
解法一:假设存在符合条件的 Ω, 可知Ω(A) 的第1, 2 项之和为a + a + s ,第3, 4 项之和为
1 2
a + a + s ,
3 4
[ ( a 2 ) a 6)
1 2
则{ ,而该方程组无解,故假设不成立,
( a 4 (a 2 )
l 3 4
故不存在符合条件的 Ω ;
解法二:由题意可知:对于任意序列,所得数列之和比原数列之和多
4, 假设存在符合条件的 Ω,且Ω(A): b , b , ..., b ,
1 2 8
因为 = 8 ,即序列 Ω共有 8 项,
由题意可知:(b + b )− (a + a ) = 8, n = 1,2,
2n−1 2n 2n−1 2n
3,4 , 检验可知:当n =2,3 时,上式不成立,
第20页/共25页即假设不成立,所以不存在符合条件的 Ω
. 【小问 3 详解】
解法一:我们设序列T ...T T (A) 为 { a }(1 ≤ n ≤ 8) ,特别规定a = a (1 ≤ n ≤ 8) .
s 2 1 s ,n 0,n n
必要性:
若存在序列Ω : T , T , …T ,使得Ω(A) 的各项都相等.
1 2 s
则 a a a a a a a a ======= ,所以a + a = a + a = a + a = a
sssssss s,1,2,3,4,5,6,7 ,8 s,1 s,2 s,3 s,4 s,5 s,6 s,7
+ a . 根据T ...T T (A) 的定义,显然有a + a = a + a +1 ,这里j = 1,2, 3,4 ,s
s,8 s 2 1 s,2j −1 s,2j s−1,2j −1 s−1,2j
= 1, 2, ... .
所以不断使用该式就得到a + a = a + a = a + a = a + a = a + a − s ,必要性
1 2 3 4 5 6 7 8 s,1 s,2
得证. 充分性:
若 a + a = a + a = a + a = a + a .
1 2 3 4 5 6 7 8
由已知,a + a + a + a 为偶数,而 a + a = a + a = a + a = a +
1 3 5 7 1 2 3 4 5 6 7
a ,所以 a + a + a + a = 4 (a + a )− (a + a + a + a ) 也是偶
8 2 4 6 8 1 2 1 3 5 7
数.
我们设T ...T T (A) 是通过合法的序列 Ω的变换能得到的所有可能的数列Ω(A) 中,
s 2 1
使得 a − a + a − a + a − a + a − a 最小的一个.
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
上面已经说明a + a = a + a +1 ,这里 j = 1,2, 3,4 ,s = 1, 2,
s,2j −1 s,2j s−1,2j −1 s−1,2j
... . 从而由a + a = a + a = a + a = a + a 可得
1 2 3 4 5 6 7 8
a s,1 + a s,2 = a s,3 + a s,4 = a s,5 + a s,6 = a s,7 + a s,8 = a 1 + a 2 + s .
同时,由于i + j + k + w 总是偶数,所以a + a + a + a 和a + a + a + a 的奇偶
t t t t t ,1 t,3 t,5 t ,7 t ,2 t ,4 t ,6 t ,8
性保持不 变,从而a + a + a + a 和a + a + a + a 都是偶数.
s,1 s,3 s,5 s,7 s,2 s,4 s,6 s,8
下面证明不存在j = 1,2, 3,4 使得a − a ≥ 2 .
s,2j −1 s,2j
假设存在,根据对称性,不妨设j = 1 ,a − a ≥ 2 ,即 a − a ≥ 2 .
s,2j −1 s,2j s,1 s,2
情况 1:若 a − a + a − a + a − a = 0 ,则由a + a + a + a 和a + a + a +
s,3 s,4 s,5 s,6 s,7 s,8 s,1 s,3 s,5 s,7 s,2 s,4 s,6
a 都 是偶数,知 a − a ≥ 4 .
s,8 s,1 s,2
对该数列连续作四次变换(2,3,5,8), (2, 4, 6,8), (2,3, 6, 7), (2, 4,5, 7) 后,新的
第21页/共25页a − a + a − a + a − a + a − a 相比原来的
s+4,1 s+4,2 s+4,3 s+4,4 s+4,5 s+4,6 s+4,7 s+4,8
a − a + a − a + a − a + a − a 减少4 ,这
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
与 a − a + a − a + a − a + a − a 的最小
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
性矛盾;
情况 2:若 a − a + a − a + a − a > 0 ,不妨设a − a > 0 .
s,3 s,4 s,5 s,6 s,7 s,8 s,3 s,4
情况 2-1:如果a − a ≥ 1 ,则对该数列连续作两次变换(2, 4,5, 7), (2, 4, 6,8) 后,
s,3 s,4
新的 a − a + a − a + a − a + a − a 相比原来的
s+2,1 s+2,2 s+2,3 s+2,4 s+2,5 s+2,6 s+2,7 s+2,8
a − a + a − a + a − a + a − a 至少减少2 ,
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
这与 a − a + a − a + a − a + a − a 的最小性
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
矛盾;
情况 2-2:如果a − a ≥ 1 ,则对该数列连续作两次变换(2,3,5,8), (2,3, 6, 7)后,新
s,4 s,3
的 a − a + a − a + a − a + a − a 相比原来的
s+2,1 s+2,2 s+2,3 s+2,4 s+2,5 s+2,6 s+2,7 s+2,8
a − a + a − a + a − a + a − a 至少减少2 ,
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
这与 a − a + a − a + a − a + a − a 的最小性
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
矛盾.
这就说明无论如何都会导致矛盾,所以对任意的j = 1,2, 3,4 都有a − a ≤ 1 .
s,2j −1 s,2j
假设存在j = 1,2, 3,4 使得a − a = 1,则a + a 是奇数,所
s,2j −1 s,2j s,2j −1 s,2j
以 a + a = a + a = a + a = a + a 都是奇数,设为2N
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
+ 1 .
则此时对任意j = 1,2, 3,4 ,由 a − a ≤ 1 可知必有 { a , a } = {N, N +1} .
s,2j −1 s,2j s,2j −1 s,2j
而a + a + a + a 和a + a + a + a 都是偶数,故集合 { m a = N } 中的四个元素i, j, k,
s,1 s,3 s,5 s,7 s,2 s,4 s,6 s,8 s ,m
w 之 和为偶数,对该数列进行一次变换(i, j, k, w) ,则该数列成为常数列,新的
a − a + a − a + a − a + a − a 等于零,比原来的
s+1,1 s+1,2 s+1,3 s+1,4 s+1,5 s+1,6 s+1,7 s+1,8
a − a + a − a + a − a + a − a 更小,这与
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
a − a + a − a + a − a + a − a 的最小性矛
s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
盾.
综上,只可能 a − a = 0 (j = 1,2,3,4),而a + a = a + a = a + a = a + a
s,2j −1 s,2j s,1 s,2 s,3 s,4 s,5 s,6 s,7 s,8
第22页/共25页,故 { a } = Ω (A) 是常数列,充分性得证.
s ,n
第22页/共25页解法二:由题意可知: Ω中序列的顺序不影响Ω(A) 的结
果, 且(a , a ), (a , a ), (a , a ), (a , a ) 相对于序列也
1 2 3 4 5 6 7 8
是无序的,
( ⅰ )若 a + a = a + a = a + a = a
1 2 3 4 5 6 7
+ a , 不妨设a ≤ a ≤ a ≤ a ,则 a ≥ a
8 1 3 5 7 2 4
≥ a ≥ a , ①当 a a a a === ,则 a
6 8 1357
a a a === ,
8642
分别执行a 个序列(2, 4, 6,8) 、a 个序列(1,3,5, 7),
1 2
可得a + a , a + a , a + a , a + a , a + a , a + a , a + a , a + a ,为常数列,符合题意;
1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2
②当a , a , a , a 中有且仅有三个数相等,不妨设a = a = a ,则 a = a =
1 3 5 7 1 3 5 2 4
a , 即 a a a a a a a a ,,,,,,, ,
6 12121278
分别执行a 个序列(1,3,5, 7) 、a 个序列(2, 4, 6,8)
2 7
可得a + a , a + a , a + a , a + a , a + a , a + a , a + a ,
1 2 2 7 1 2 2 7 1 2 2 7 2 7
a + a , 即 a + a , a + a , a + a , a + a , a + a , a + a
7 8 1 2 2 7 1 2 2 7 1 2 2 7
, a + a , a + a ,
2 7 1 2
因为a + a + a + a 为偶数,即3a + a 为偶数,
1 3 5 7 1 7
可知a , a 的奇偶性相同,则 ∈ N* ,
1 7
( ) ( ) ( ) ( )
分别执行 个序列 1,3,5, 7 , 1, 3, 6,8 , 2,3,5,8 , 1, 4,5,8 ,
可得
3a + 2a − a 3a + 2a − a 3a + 2a − a 3a + 2a − a 3a + 2a − a 3a + 2a − a 3a + 2a −
7 2 1 7 2 1 7 2 1 7 2 1 7 2 1 7 2 1 7 2
a 3a + 2a
, , , , , , 1 , 7
2 2 2 2 2 2 2 2
,
为常数列,符合题意;
③若a = a < a = a ,则 a = a > a = a ,即 a a a a a a a
1 3 5 7 2 4 6 8
a ,,,,,,, , 分别执行a 个(1, 3, 6,8) 、 a 个(2, 4,5, 7),
12125656 5 1
可得a + a , a + a , a + a , a + a , a + a , a + a , a + a ,
1 5 1 2 1 5 1 2 1 5 5 6 1 5
a + a , 因为a + a = a + a ,
5 6 1 2 5 6
可得a + a , a + a , a + a , a + a , a + a , a + a , a + a , a + a ,
1 5 1 2 1 5 1 2 1 5 1 2 1 5 1 2
第23页/共25页即转为①,可知符合题意;
④当a , a , a , a 中有且仅有两个数相等,不妨设a = a ,则 a =
1 3 5 7 1 3 2
a , 即 a a a a a a a a ,,,,,,, ,
4 12125678
分别执行a 个(2, 4,5, 7) 、a 个(1, 3, 6,8) ,
1 5
可得a + a , a + a , a + a , a + a , a + a , a + a , a + a , a + a ,
1 5 1 2 1 5 1 2 1 5 5 6 1 7 5 8
且 a + a = a + a ,可得a + a , a + a , a + a , a + a , a + a , a + a , a +
1 2 5 6 1 5 1 2 1 5 1 2 1 5 1 2 1
a , a + a , 因为a + a + a + a = 2a + a + a 为偶数,可知a , a 的奇偶性相
7 5 8 1 3 5 7 1 5 7 5 7
同,
则(a + a ) + (a + a ) + (a + a ) + (a + a ) = 4a + 3a
1 5 1 5 1 5 1 7 1 5
+ a 为偶数, 且 a + a = a + a = a + a < a + a ,即转为
7 1 5 1 5 1 5 1 7
②, 可知符合题意;
⑤若a < a < a < a ,则 a > a > a > a ,即 a a a a a a a
1 3 5 7 2 4 6 8
a ,,,,,,, , 分别执行a 个(2,3,5,8) 、a 个(1, 4, 6, 7),
12345678 1 3
可得a + a , a + a , a + a , a + a , a + a , a + a , a + a , a + a ,
1 3 1 2 1 3 3 4 1 5 3 6 3 7 1 8
且 a + a = a + a ,可得a + a , a + a , a + a , a + a , a + a , a + a , a +
1 2 3 4 1 3 1 2 1 3 1 2 1 5 3 6 3
a , a + a , 因为a + a + a + a 为偶数,
7 1 8 1 3 5 7
则(a + a ) + (a + a ) + (a + a ) + (a + a ) = 2 (a + a ) + (a + a +
1 3 1 3 1 5 3 7 1 3 1 3
a + a ) 为偶数, 且 a + a = a + a < a + a < a + a ,即转为 ④,可知符
5 7 1 3 1 3 1 5 3 7
合题意;
综上所述:若a + a = a + a = a + a = a + a ,则存在序列 Ω , 使得Ω(A) 为常数列;
1 2 3 4 5 6 7 8
(ⅱ)若存在序列 Ω ,使得Ω(A) 为常数
列, 因为对任意Ω(A): b , b , ..., b ,
1 2 8
均有(b + b )− (a + a ) = (b + b )− (a + a ) = (b + b )− (a + a ) = (b + b )−
1 2 1 2 3 4 3 4 5 6 5 6 7 8
(a + a ) 成立,
7 8
若Ω(A) 为常数列,则b + b = b + b = b + b = b
1 2 3 4 5 6 7
+ b , 所以a + a = a + a = a + a = a + a ;
8 1 2 3 4 5 6 7 8
综上所述:“存在序列 Ω , 使得Ω(A) 为常数列” 的充要条件为“ a + a = a + a = a + a = a
1 2 3 4 5 6 7
+ a ”.
8
第24页/共25页【点睛】关键点点睛:本题第三问的关键在于对新定义的理解,以及对其本质的分析.
第25页/共25页