文档内容
2023 学年第二学期高二数学学科测试卷(五)
命题人:崔舒静 审题人:詹长刚
一. 单选题:本题共8小题,每小题5分,共40分
1、.已知集合M={y|y=ln(1−x❑ 2)},N={x|−10,|φ|< 的图象上,且图象过点 ,2 ,相邻最大值与最小值之间的水平距离为
2 24
π
,则是函数的单调递增区间的是( )
2
π π 7π 5π 5π 3π 5π 3π
A.[− ,− ] B.[− , ] C.[ , ] D.[ , ]
3 4 24 24 24 8 8 4
第 1 页
学科网(北京)股份有限公司{
lnx+x,x>1
7、.已知函数f (x)= m ,若g(x)=f (x)−m有三个零点,则实数m的取值范围是(
2x2−mx+ ,x≤1
2
)
7 4
A.(1, ] B.(1,2] C.(1, ] D.[1,3]
4 3
8、.张衡是中国东汉时期伟大的天文学家、数学家,他曾在数学著作《算罔论》中得出结论:圆周率的
平方除以十六约等于八分之五. 已知在菱形ABCD中,AB=BD=2√3,将△ABD沿BD进行翻折,使得
AC=2√6. 那么三棱锥A−BCD外接球表面积约为( )
A.72 B.24√10 C.28√10 D.32√10
二. 多选题:本题共3小题,每小题6分,共18分,在每小题给出的选项中有多项符合题目
要求,全部选对得6分,部分选对得3分,有选错的得0分.
1
9、.在△ABC中,D为边AC上的一点,且满足⃗AD= ⃗DC,若P为边BD上的一点,且满足
2
⃗AP=m⃗AB+n⃗AC(m>0,n>0),则下列结论正确的是( )
1
A.m+2n=1 B.mn的最大值为
12
4 1 1
C. + 的最小值为6+4√2 D.m❑ 2+9n❑ 2的最小值为
m n 2
10、.对于数列{a },若存在正数M,使得对一切正整数n,都有|a |≤M,则称数列{a }是有界的. 若这
n n n
样的正数M不存在,则称数列{a }是无界的. 记数列{a }的前n项和为S ,下列结论正确的是( )
n n n
1 (1) n
A.若a = ,则数列{a }是无界的 B.若a = sinn,则数列{S }是有界的
n n n n 2 n
1
C.若a =(−1)❑ n,则数列{S }是有界的 D.若a =2+ ,则数列{S }是有界的
n n n n❑ 2 n
11、.已知函数f (x)及其导函数f′(x)的定义域均为R,若f (x)是奇函数,f (2)=−f (1)≠0,且对任意x,
y∈R,f (x+ y)=f (x)f❑ ′(y)+f❑ ′(x)f (y),则( )
1 20 20
A.f❑ ′(1)= B.f (9)=0 C.∑ f (k)=1 D.∑ f′(k)=−1
2
k=1 k=1
三. 填空题:本题共3小题,每小题5分,共15分.
12、.已知复数z满足z=(1+2i)(1+i)(其中i为虚数单位),则|z|= .
13、.学校一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,则在课表上
的相邻两节文化课之间最多间隔1节艺术课的概率为 (用数字作答).
14、.已知⊙O :x2+(y−2) 2=1,⊙O :(x−3) 2+(y−6) 2=9,过x轴上一点P分别作两圆的切线,切点
1 2
分别是M,N,求|PM|+|PN|的最小值为 .
四. 解答题:本题共5小题,共77分,其中第15题13分,第16题和第17题每题15分,第
18题和第19题每题17分,解答题应写出文字说明、证明过程或演算步骤.
15、.已知△ABC的角A,B,C的对边分别为a,b,c,且
sin A(ccosB+bcosC)−csinB=csinC+bsinB.
(1)求角A;
(2)若AD平分∠BAC交线段BC于点D,且AD=2,BD=2CD,求△ABC的周长.
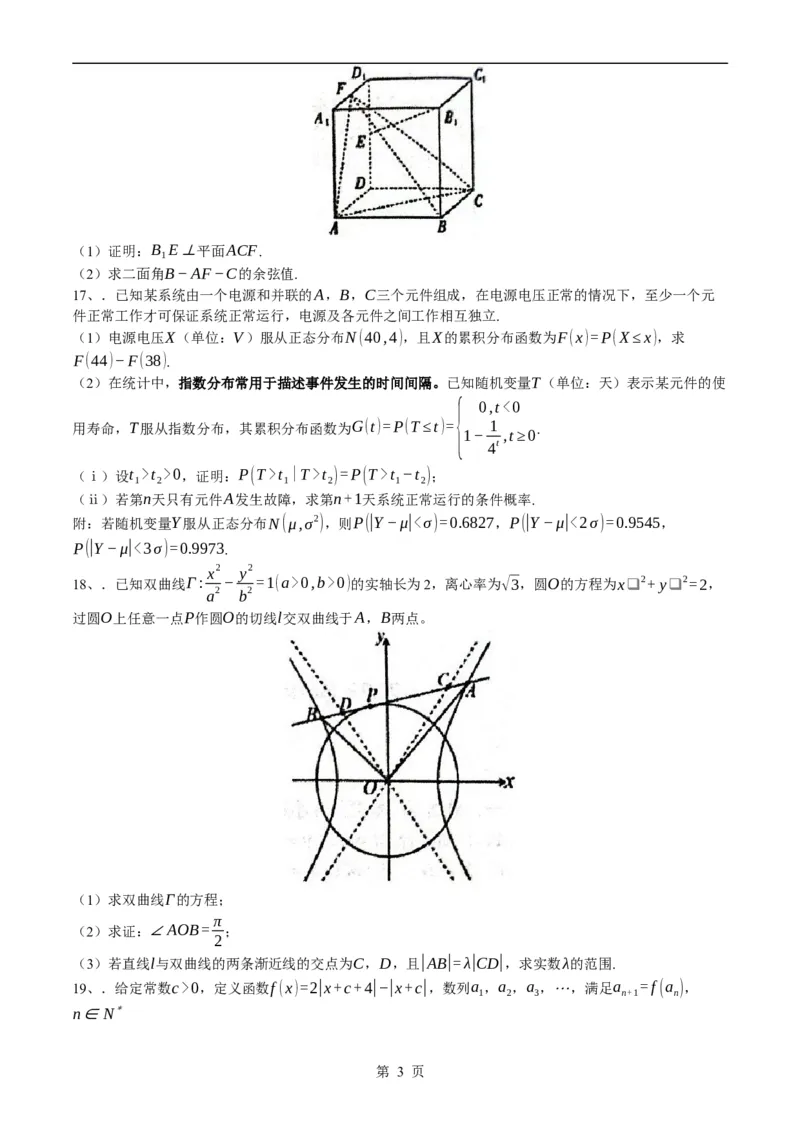
16、.如图,在正方体ABCD−A B C D 中,E,F分别是棱DD ,A D 的中点.
1 1 1 1 1 1 1
第 2 页
学科网(北京)股份有限公司(1)证明:B E⊥平面ACF.
1
(2)求二面角B−AF−C的余弦值.
17、.已知某系统由一个电源和并联的A,B,C三个元件组成,在电源电压正常的情况下,至少一个元
件正常工作才可保证系统正常运行,电源及各元件之间工作相互独立.
(1)电源电压X(单位:V)服从正态分布N(40,4),且X的累积分布函数为F(x)=P(X≤x),求
F(44)−F(38).
(2)在统计中,指数分布常用于描述事件发生的时间间隔。已知随机变量T(单位:天)表示某元件的使
{
0,t<0
用寿命,T服从指数分布,其累积分布函数为G(t)=P(T≤t)= 1 .
1− ,t≥0
4t
(ⅰ)设t >t >0,证明:P(T>t |T>t )=P(T>t −t );
1 2 1 2 1 2
(ⅱ)若第n天只有元件A发生故障,求第n+1天系统正常运行的条件概率.
附:若随机变量Y服从正态分布N(μ,σ2),则P(|Y−μ|<σ)=0.6827,P(|Y−μ|<2σ)=0.9545,
P(|Y−μ|<3σ)=0.9973.
x2 y2
18、.已知双曲线Γ: − =1(a>0,b>0)的实轴长为2,离心率为√3,圆O的方程为x❑ 2+ y❑ 2=2,
a2 b2
过圆O上任意一点P作圆O的切线l交双曲线于A,B两点。
(1)求双曲线Γ的方程;
π
(2)求证:∠AOB= ;
2
(3)若直线l与双曲线的两条渐近线的交点为C,D,且|AB|=λ|CD|,求实数λ的范围.
19、.给定常数c>0,定义函数f (x)=2|x+c+4|−|x+c|,数列a ,a ,a ,⋯,满足a =f (a ),
1 2 3 n+1 n
n∈N∗
第 3 页
学科网(北京)股份有限公司(1)若a =−c−2,求a 及a ;
1 2 3
(2)求证:对任意n∈N∗,a −a ≥c
n+1 n
(3)是否存在a ,使得a ,a ,⋯,a ,⋯成等差数列?若存在,求出所有这样的a ,若不存在,说明
1 1 2 n 1
理由
第 4 页
学科网(北京)股份有限公司