文档内容
2024年新高考改革适应性练习 2(九省联考题型)
数学参考答案
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.)
题号 1 2 3 4 5 6 7 8
答案 A D C B B A D C
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得3分,有选错的得0分.)
题号 9 10 11
答案 CD ABC BD
三、填空题(本题共3小题,每小题5分,共15分.)
题号 12 13 14
答案 2或-2 或 75
1 3 1
𝑒𝑒+ 8+𝑒𝑒 + 3
𝑒𝑒 𝑒𝑒
四、解答题(本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.)
15.(13分)
(1)由题意得,
tan𝐴𝐴+tan𝐵𝐵−√3tan𝐴𝐴tan𝐵𝐵 = −√3
⟺ tan𝐴𝐴+tan𝐵𝐵 = −√3(1−tan𝐴𝐴tan𝐵𝐵)
tan𝐴𝐴+tan𝐵𝐵
⟺ = −√3
1−tan𝐴𝐴tan𝐵𝐵
⟺ tan(𝐴𝐴+𝐵𝐵) = −√3
𝜋𝜋
⟺tan𝐶𝐶 = −tan(𝐴𝐴+𝐵𝐵) = √3 ⟺ 𝐶𝐶 =
所以 . 3
𝜋𝜋
(2) 𝐶𝐶由=正3弦 定理,
数学参考答案 第1页(共6页)
学科网(北京)股份有限公司1 1 𝜋𝜋 √3
由题意 ,又 ,𝑆𝑆由=基本sin不𝐶𝐶等𝑎𝑎𝑎𝑎式=得 ·sin ·𝑎𝑎𝑎𝑎 = 𝑎𝑎𝑎𝑎
2 2 3 4
𝑎𝑎+𝑎𝑎 = 4 𝑎𝑎,𝑎𝑎 > 0
解得 ,
𝑎𝑎+𝑎𝑎 = 4 ≥ 2√𝑎𝑎𝑎𝑎
所以 𝑎𝑎𝑎𝑎 ≤ 4
√3 √3
故 的最大值为 ,取等时 𝑆𝑆,=即 𝑎𝑎𝑎𝑎 ≤ 是×一4个=正√三3角形.
4 4
𝑆𝑆 √3 𝑎𝑎 = 𝑎𝑎 = 2 △𝐴𝐴𝐵𝐵𝐶𝐶
16.(15分)
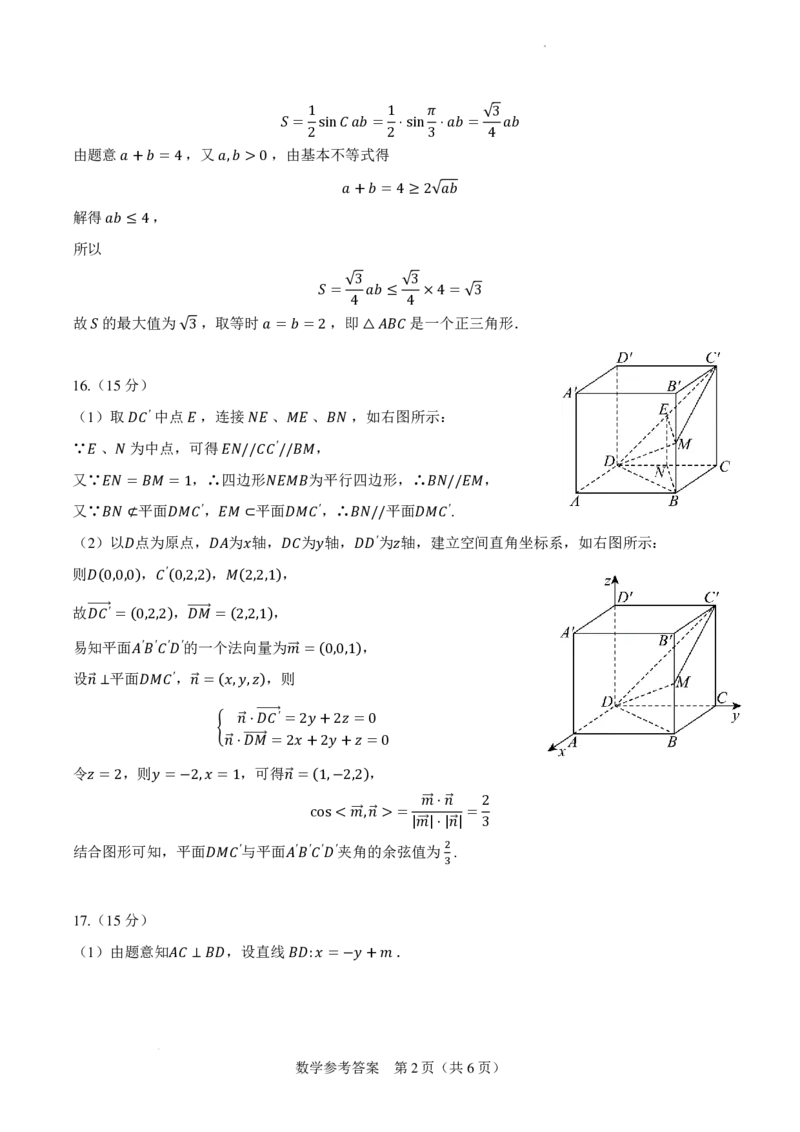
(1)取 ′中点 ,连接 、 、 ,如右图所示:
∵ 、 𝐷𝐷为𝐶𝐶中 点, 𝐸𝐸可 得 𝑁𝑁𝐸𝐸 ′ 𝑀𝑀𝐸𝐸 ,𝐵𝐵 𝑁𝑁
又𝐸𝐸∵ 𝑁𝑁 ,∴ 𝐸𝐸四𝑁𝑁边//形𝐶𝐶𝐶𝐶//𝐵𝐵𝑀𝑀为平行四边形,∴ ,
又∵𝐸𝐸𝑁𝑁 =平𝐵𝐵𝑀𝑀面= 1 ′, 平𝑁𝑁面𝐸𝐸𝑀𝑀𝐵𝐵 ′,∴ 平面 𝐵𝐵𝑁𝑁/′. /𝐸𝐸𝑀𝑀
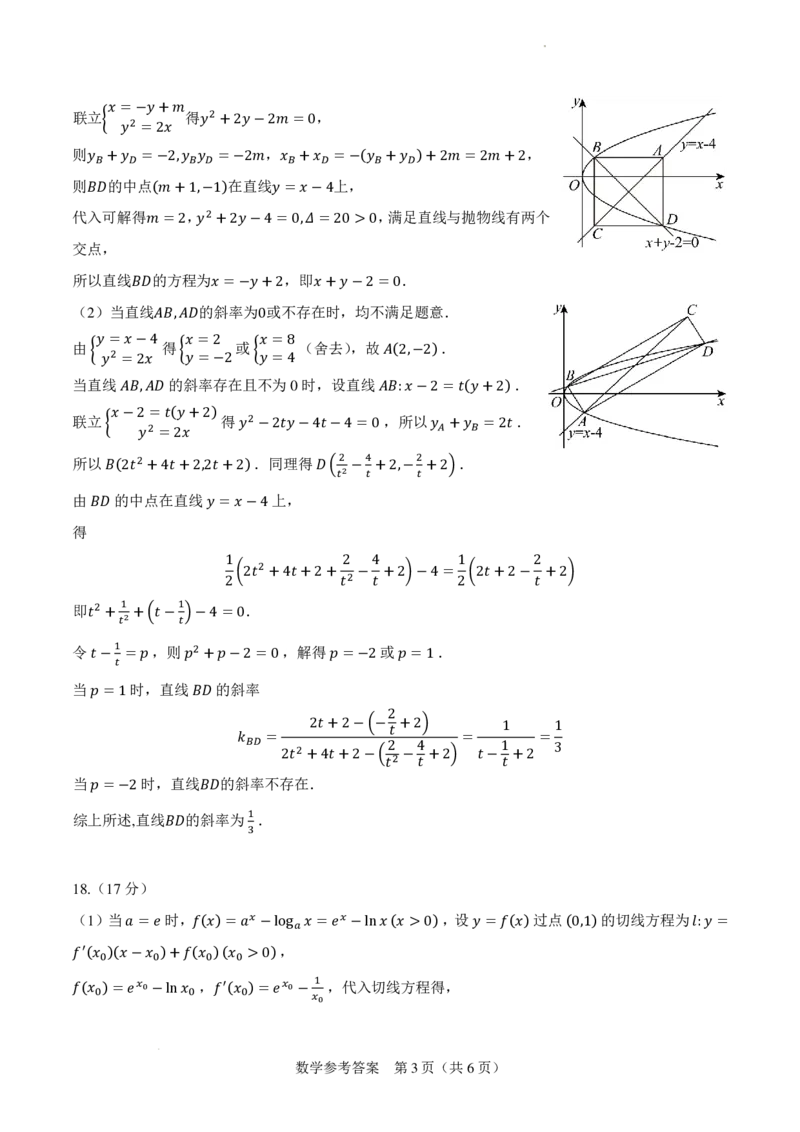
(2)𝐵𝐵以𝑁𝑁 ⊄点为原𝐷𝐷𝑀𝑀点𝐶𝐶, 𝐸𝐸𝑀𝑀为⊂轴,𝐷𝐷𝑀𝑀为𝐶𝐶 轴,𝐵𝐵𝑁𝑁/′/为 轴𝐷𝐷,𝑀𝑀建𝐶𝐶立空间直角坐标系,如右图所示:
则 𝐷𝐷 , ′ 𝐷𝐷,𝐴𝐴 𝑥𝑥 𝐷𝐷,𝐶𝐶 𝑦𝑦 𝐷𝐷𝐷𝐷 𝑧𝑧
𝐷𝐷(0,0,0) 𝐶𝐶(0,2,2) 𝑀𝑀(2,2,1)
故 ′ , ,
易知𝐷𝐷 ����� 𝐶𝐶 � 平 �⃗ =面(0′,2′,2′) ′的𝐷𝐷����𝑀𝑀一��⃗个=法(2向,2,量1)为 ,
设 平面𝐴𝐴𝐵𝐵𝐶𝐶𝐷𝐷′, ,则𝑚𝑚��⃗ = (0,0,1)
𝑛𝑛�⃗ ⊥ 𝐷𝐷𝑀𝑀𝐶𝐶 𝑛𝑛�⃗ = (𝑥𝑥,𝑦𝑦,𝑧𝑧)
′
�������⃗
𝑛𝑛�⃗⋅𝐷𝐷𝐶𝐶 = 2𝑦𝑦+2𝑧𝑧 = 0
�
令 ,则 𝑛𝑛�⃗⋅,𝐷𝐷����𝑀𝑀可��⃗得= 2𝑥𝑥+2𝑦𝑦+𝑧𝑧 =,0
𝑧𝑧 = 2 𝑦𝑦 = −2,𝑥𝑥 = 1 𝑛𝑛�⃗ = (1,−2,2)
𝑚𝑚��⃗⋅𝑛𝑛�⃗ 2
cos< 𝑚𝑚��⃗,𝑛𝑛�⃗ > = =
结合图形可知,平面 ′与平面 ′ ′ ′ ′夹角的余弦值|𝑚𝑚��⃗为|⋅|𝑛𝑛�⃗. | 3
2
𝐷𝐷𝑀𝑀𝐶𝐶 𝐴𝐴𝐵𝐵𝐶𝐶𝐷𝐷 3
17.(15分)
(1)由题意知 ,设直线 .
𝐴𝐴𝐶𝐶 ⊥ 𝐵𝐵𝐷𝐷 𝐵𝐵𝐷𝐷:𝑥𝑥 = −𝑦𝑦+𝑚𝑚
数学参考答案 第2页(共6页)
学科网(北京)股份有限公司联立 得 ,
𝑥𝑥 = −𝑦𝑦+𝑚𝑚 2
则 �
𝑦𝑦
2
= 2𝑥𝑥
𝑦𝑦 +2𝑦𝑦−,2𝑚𝑚 = 0 ,
则𝑦𝑦𝐵𝐵 +的𝑦𝑦中𝐷𝐷点= −2,𝑦𝑦𝐵𝐵𝑦𝑦𝐷𝐷 =在−直2𝑚𝑚线 𝑥𝑥𝐵𝐵 +𝑥𝑥𝐷𝐷 =上,−( 𝑦𝑦𝐵𝐵 +𝑦𝑦𝐷𝐷)+2𝑚𝑚 = 2𝑚𝑚+2
代入𝐵𝐵𝐷𝐷可解得 (𝑚𝑚+,1,−1) 𝑦𝑦 = 𝑥𝑥−4 ,满足直线与抛物线有两个
2
交点, 𝑚𝑚 = 2 𝑦𝑦 +2𝑦𝑦−4 = 0,𝛥𝛥 = 20> 0
所以直线 的方程为 ,即 .
(2)当直𝐵𝐵线𝐷𝐷 的𝑥𝑥斜=率−为𝑦𝑦+或2不存在𝑥𝑥+时𝑦𝑦,−均2不=满0足题意.
由 𝐴𝐴得𝐵𝐵,𝐴𝐴𝐷𝐷 或 0 (舍去),故 .
𝑦𝑦 = 𝑥𝑥−4 𝑥𝑥 = 2 𝑥𝑥 = 8
当 直� 𝑦𝑦 线 2 = 2𝑥𝑥 的 �斜 𝑦𝑦 = 率存 −2 在 且 �不 𝑦𝑦 为 = 40 时,设直线 𝐴𝐴(2,−2) .
联立 𝐴𝐴𝐵𝐵,𝐴𝐴𝐷𝐷 得 𝐴𝐴,𝐵𝐵所:𝑥𝑥以−2 = 𝑡𝑡(𝑦𝑦+2) .
𝑥𝑥−2 = 𝑡𝑡(𝑦𝑦+2) 2
� 2 𝑦𝑦 −2𝑡𝑡𝑦𝑦−4𝑡𝑡−4 = 0 𝑦𝑦𝐴𝐴 +𝑦𝑦𝐵𝐵 = 2𝑡𝑡
所以 𝑦𝑦 = 2𝑥𝑥 .同理得 .
2 2 4 2
2
由 𝐵𝐵的(2中𝑡𝑡 点+在4𝑡𝑡直+线2,2𝑡𝑡+2) 上, 𝐷𝐷�𝑡𝑡 −𝑡𝑡 +2,−𝑡𝑡 +2�
得 𝐵𝐵𝐷𝐷 𝑦𝑦 = 𝑥𝑥−4
1 2 2 4 1 2
�2𝑡𝑡 +4𝑡𝑡+2+ 2− +2�−4 = �2𝑡𝑡+2− +2�
即 2 . 𝑡𝑡 𝑡𝑡 2 𝑡𝑡
2 1 1
2
𝑡𝑡 +𝑡𝑡 +�𝑡𝑡−𝑡𝑡�−4 = 0
令 ,则 ,解得 或 .
1 2
当 𝑡𝑡−𝑡𝑡 =时𝑝𝑝, 直线 𝑝𝑝 +的𝑝𝑝−斜2率= 0 𝑝𝑝 = −2 𝑝𝑝 = 1
𝑝𝑝 =1 𝐵𝐵𝐷𝐷
2
2𝑡𝑡+2−�− +2� 1 1
𝑡𝑡
𝑘𝑘𝐵𝐵𝐷𝐷 = = =
当 时,直线 的斜率不存2𝑡𝑡在 2 +.4 𝑡𝑡+2−� 2 2− 4 +2� 𝑡𝑡− 1 +2 3
𝑡𝑡 𝑡𝑡 𝑡𝑡
综 上𝑝𝑝所=述−2 ,直 线 的𝐵𝐵斜𝐷𝐷率为 .
1
𝐵𝐵𝐷𝐷 3
18.(17分)
(1)当 时, ,设 过点 的切线方程为
𝑥𝑥 𝑥𝑥
𝑎𝑎 = 𝑒𝑒 𝑓𝑓(𝑥𝑥)= 𝑎𝑎 −lo,g𝑎𝑎 𝑥𝑥 = 𝑒𝑒 −ln𝑥𝑥(𝑥𝑥 > 0) 𝑦𝑦 = 𝑓𝑓(𝑥𝑥) (0,1) 𝑙𝑙:𝑦𝑦 =
′
𝑓𝑓 (𝑥𝑥0)(𝑥𝑥−𝑥𝑥0)+𝑓𝑓(𝑥𝑥,0) (𝑥𝑥0 > 0) ,代入切线方程得,
𝑥𝑥0 ′ 𝑥𝑥0 1
𝑓𝑓(𝑥𝑥0)= 𝑒𝑒 −ln𝑥𝑥0 𝑓𝑓 (𝑥𝑥0)= 𝑒𝑒 −𝑥𝑥0
数学参考答案 第3页(共6页)
学科网(北京)股份有限公司𝑥𝑥0 1 𝑥𝑥0 𝑥𝑥0 1 𝑥𝑥0
因为 过点 𝑦𝑦 = �,𝑒𝑒所−以
𝑥𝑥0
�(𝑥𝑥−𝑥𝑥0)+𝑒𝑒 −ln𝑥𝑥0 =,�𝑒𝑒即−
𝑥𝑥0
�𝑥𝑥+𝑒𝑒 (1−𝑥𝑥0)−,ln 𝑥𝑥0+1
𝑥𝑥0 𝑥𝑥0
令 𝑙𝑙 (0,1) 𝑒𝑒 ,(1−𝑥𝑥0)−ln𝑥𝑥0+1 = 1, 所以 𝑒𝑒 (1−单𝑥𝑥调 0)递−减ln,𝑥𝑥0 又= 0 ,所以 有
𝑥𝑥 ′ 𝑥𝑥 1
唯一 𝑔𝑔(零𝑥𝑥)点= 𝑒𝑒 (1−,𝑥𝑥即)原−方ln程𝑥𝑥 的𝑔𝑔根(为𝑥𝑥)= −𝑥𝑥𝑒𝑒, − 𝑥𝑥 < 0 𝑔𝑔(𝑥𝑥) 𝑔𝑔(1)= 0 𝑔𝑔(𝑥𝑥)
代回切线 方𝑥𝑥程=得1 𝑥𝑥 = 1
𝑥𝑥0 1 𝑥𝑥0
故 过点 𝑦𝑦的=切�线𝑒𝑒 方−程
𝑥𝑥
为
0
�𝑥𝑥+𝑒𝑒 (1−𝑥𝑥0)−.ln 𝑥𝑥0+1 = (𝑒𝑒−1)𝑥𝑥+1
(2 𝑦𝑦)=因𝑓𝑓为(𝑥𝑥) 在 (0,1) 上连续,又 𝑦𝑦 = (𝑒𝑒−1)𝑥𝑥+,1 所以要使 无零点,需使 在其定义
域上恒成立 𝑓𝑓.(𝑥𝑥 ) (0,+∞) 𝑓𝑓(1)= 𝑎𝑎 > 0 𝑓𝑓(𝑥𝑥) 𝑓𝑓(𝑥𝑥) > 0
则原问题转化为 ,求 的取值范围,
𝑥𝑥
𝑓𝑓(𝑥𝑥)= 𝑎𝑎 −log𝑎𝑎𝑥𝑥 > 0 𝑎𝑎
𝑥𝑥 𝑥𝑥 𝑥𝑥 ln𝑥𝑥
𝑎𝑎 −log𝑎𝑎𝑥𝑥 > 0 ⟺𝑎𝑎 > log𝑎𝑎𝑥𝑥 ⟺𝑎𝑎 >
ln𝑎𝑎
𝑥𝑥 𝑥𝑥 𝑥𝑥 𝑥𝑥
令 ⟺,𝑎𝑎 ln𝑎𝑎 > ln𝑥𝑥 ⟺ 𝑎𝑎 𝑥𝑥ln,𝑎𝑎 >所𝑥𝑥以ln𝑥𝑥 ⟺单𝑎𝑎调l递n𝑎𝑎增,> 𝑥𝑥ln𝑥𝑥 (∗)
𝑥𝑥 ′ 𝑥𝑥
又由 ℎ(𝑥𝑥)=式𝑥𝑥得𝑒𝑒 (𝑥𝑥 > 0) ℎ (𝑥𝑥)=,(𝑥𝑥所+以1)𝑒𝑒 > 0 ℎ(𝑥𝑥) ,即 恒成立.
𝑥𝑥 𝑥𝑥 ln𝑥𝑥
(∗) ℎ(ln𝑎𝑎 )> ℎ(ln𝑥𝑥) ln𝑎𝑎 = 𝑥𝑥ln𝑎𝑎 > ln𝑥𝑥 ln𝑎𝑎 > 𝑥𝑥
令 , ,令 得 ,
ln𝑥𝑥 ′ 1−ln𝑥𝑥 ′
2
当 𝜑𝜑(𝑥𝑥)= 𝑥𝑥时 ,𝜑𝜑 (𝑥𝑥)= 𝑥𝑥, 𝜑𝜑单(调𝑥𝑥)递=增0; 当 𝑥𝑥 = 𝑒𝑒 时, , 单调递减,
′ ′
所以 0 < 𝑥𝑥 <是𝑒𝑒 𝜑𝜑的 (𝑥𝑥极 ) 大>值0 点𝜑𝜑, (𝑥𝑥) 𝑥𝑥 >,𝑒𝑒 所以𝜑𝜑 (𝑥𝑥)<,0 即𝜑𝜑(𝑥𝑥) .
1
1 1 𝑒𝑒
𝑥𝑥 =𝑒𝑒 𝜑𝜑(𝑥𝑥) 𝜑𝜑(𝑥𝑥)max = 𝜑𝜑(𝑒𝑒)= 𝑒𝑒 ln𝑎𝑎 > 𝑒𝑒 𝑎𝑎 > 𝑒𝑒
综上所述, 的取值范围为 .
1
𝑒𝑒
𝑎𝑎 �𝑒𝑒 ,+∞�
19.(17分)
(1)设 的分布列为 其中 , ,
则对任意 𝑋𝑋 , 𝑃𝑃(𝑋𝑋 = 𝑥𝑥𝑖𝑖) = 𝑝𝑝𝑖𝑖 (𝑖𝑖 = 1,2,…,𝑛𝑛) 𝑝𝑝𝑖𝑖 ∈(0,+∞) 𝑝𝑝1+𝑝𝑝2+⋯+𝑝𝑝𝑛𝑛 = 1
𝜀𝜀 > 0
2
�𝑥𝑥𝑖𝑖 −𝐸𝐸(𝑋𝑋)� 1 2
𝑃𝑃(|𝑋𝑋−𝐸𝐸(𝑋𝑋)|≥ 𝜀𝜀)= � 𝑃𝑃𝑖𝑖 ≤ � 2 𝑃𝑃𝑖𝑖 = 2 � �𝑥𝑥𝑖𝑖 −𝐸𝐸(𝑋𝑋)� 𝑃𝑃𝑖𝑖
|𝑥𝑥𝑖𝑖−𝜇𝜇|≥𝜀𝜀 |𝑥𝑥𝑖𝑖−𝜇𝜇|≥𝜀𝜀 𝜀𝜀 𝜀𝜀 |𝑥𝑥𝑖𝑖−𝜇𝜇|≥𝜀𝜀
𝑛𝑛
1 2 𝐷𝐷(𝑋𝑋)
≤ 2��𝑥𝑥𝑖𝑖 −𝐸𝐸(𝑋𝑋)� 𝑃𝑃𝑖𝑖 = 2
(2)由切比雪夫不等式, 𝜀𝜀 𝑖𝑖=1 𝜀𝜀
数学参考答案 第4页(共6页)
学科网(北京)股份有限公司𝑛𝑛 𝑛𝑛
𝐸𝐸(𝑋𝑋𝑖𝑖) 𝐸𝐸(𝑋𝑋𝑖𝑖) 𝑛𝑛
𝐸𝐸(𝑋𝑋) = 𝐸𝐸�� � = � =
𝑖𝑖=1 𝑖𝑖 𝑖𝑖=1 𝑖𝑖 2
𝑛𝑛
2
2 𝑋𝑋𝑖𝑖 1
𝐷𝐷(𝑋𝑋)= 𝐸𝐸((𝑋𝑋−𝐸𝐸(𝑋𝑋)) )= 𝐸𝐸��� − � �
𝑖𝑖=1 𝑖𝑖 2
𝑛𝑛 𝑛𝑛 𝑛𝑛
2 2
𝑋𝑋𝑖𝑖 1 𝑋𝑋𝑖𝑖 1 𝑋𝑋𝑗𝑗 1 𝑋𝑋𝑖𝑖 1 𝑋𝑋𝑖𝑖
= �𝐸𝐸�� − � �+2 � 𝐸𝐸� − �𝐸𝐸� − �= �𝐸𝐸�� − � �= �𝐷𝐷� �
用到 𝑖𝑖=1 𝑖𝑖 2 1⩽𝑖𝑖<𝑗𝑗⩽𝑛𝑛 𝑖𝑖 2 𝑗𝑗 2 𝑖𝑖=1 𝑖𝑖 2 𝑖𝑖=1 𝑖𝑖
𝑋𝑋𝑖𝑖 1
而 𝐸𝐸� − � =0(1 ⩽ 𝑖𝑖 ⩽ 𝑛𝑛)
𝑖𝑖 2
2
𝑖𝑖 𝑗𝑗 1
𝑋𝑋𝑖𝑖 ∑𝑗𝑗=0� − � 1
𝑖𝑖 2
𝐷𝐷� �= ⩽
故 . 𝑖𝑖 𝑖𝑖+1 4
𝑛𝑛
当 𝐷𝐷(𝑋𝑋) ≤ 4时 ,
𝑛𝑛 = 160
𝑛𝑛
𝑛𝑛
因此,不能保证 𝑃𝑃(𝑋𝑋 ⩽0.1𝑛𝑛). < 𝑃𝑃��𝑋𝑋− �⩾ 0.4𝑛𝑛�⩽ 4 2 < 0.01
2 0.16𝑛𝑛
(3)由(1)已 证𝑃𝑃(得𝑋𝑋的⩽切0.比1𝑛𝑛雪)⩾夫0不.0等1 式,
𝐷𝐷(𝑋𝑋)
𝑃𝑃(|𝑋𝑋−𝐸𝐸(𝑋𝑋)|≥ 𝜀𝜀)≤ 2
𝜀𝜀 ②
𝐷𝐷(𝑋𝑋)
回到原题,设至少需要 次试验⟺,用𝑃𝑃(|𝑋𝑋表−示𝐸𝐸(𝑋𝑋次)|实<验𝜀𝜀)中≥ 1出−现的2次 数,
𝜀𝜀
则 , 𝑛𝑛 𝑋𝑋 𝑛𝑛 𝐴𝐴 ,
𝑋𝑋 𝑋𝑋
𝑋𝑋~𝐵𝐵(𝑛𝑛,0.75) 𝑃𝑃�0.74< 𝑛𝑛 < 0.76� = 𝑃𝑃��𝑛𝑛−0.75�< 0.01�
因 ,
𝑋𝑋 1 1
由 切𝐸𝐸比�𝑛𝑛雪� =夫𝑛𝑛不𝐸𝐸等(𝑋𝑋式) =(𝑛𝑛②·)𝑛𝑛,·0 .75= 0.75
𝑋𝑋 𝑋𝑋
𝑃𝑃�0.74 < < 0.76�= 𝑃𝑃�� −0.75�< 0.01�
𝑛𝑛 𝑛𝑛
𝑋𝑋 1
𝐷𝐷� � 2·𝑛𝑛·0.75·0.25
𝑛𝑛 𝑛𝑛
≥ 1− 2 = 1− 2 ≥ 0.90
解得 ,
0.01 0.01
故应 该𝑛𝑛至>少18做75108 750次试验.
数学参考答案 第5页(共6页)
学科网(北京)股份有限公司