文档内容
2024 年高三一模考试
数学试题
一、选择题: 本题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项是
符合题目要求的.
1.已知样本数据为 、 、 、 、 、 、 , 去掉一个最大值和一个最小值后的数据与原来的
数据相比, 下列数字𝑥𝑥1特征𝑥𝑥2一定𝑥𝑥3不变𝑥𝑥4的是𝑥𝑥5 𝑥𝑥6 𝑥𝑥7
A. 极差 B. 平均数 C. 中位数 D. 方差
2.已知复数 满足 , 其中 为虚数单位, 则 的虚部为
2024
A. B𝑧𝑧. 𝑧𝑧(1 +i)C=. i iD. 𝑧𝑧
1 1 1 √2
3.已−知2集合 2 −2i 2 , 则
A. B. C. D.
𝐴𝐴 = {𝑥𝑥 ∣ 𝑥𝑥 = 3𝑛𝑛,𝑛𝑛 ∈ 𝑍𝑍},𝐵𝐵 = {𝑥𝑥 ∣ 0 ≤ 𝑥𝑥 ≤ 6} 𝐴𝐴∩𝐵𝐵 =
4. 的展开式中 项的系数等于 40 , 则 是 的
{1,2} {3,6} {0,1,2} {0,3,6}
5 2 3
A. 充分不必要条件 B. 必要不充分条件
𝑝𝑝:𝑚𝑚 = 2,𝑞𝑞:(𝑚𝑚𝑥𝑥+𝑦𝑦) 𝑥𝑥 𝑦𝑦 𝑝𝑝 𝑞𝑞
C. 充要条件 D. 既不充分又不必要条件
5.已知向量 , 若 , 则
𝒂𝒂 = (sin 𝜃𝜃,cos 𝜃𝜃),𝒃𝒃 = (√2,1) 𝒂𝒂⋅𝒃𝒃 = |𝒃𝒃| tan 𝜃𝜃 =
A. B. C. D.
√2 √3
6.已2知 √2 , 其中 √3 是奇函数且在2 上为增函数, 则
A. 𝑓𝑓(𝑥𝑥) = 𝑥𝑥ℎ(𝑥𝑥) ℎ(𝑥𝑥) B.R
3 2 3 2
1 −2 −3 −2 −3 1
C.
𝑓𝑓�log2 3� > 𝑓𝑓�2 � > 𝑓𝑓�2 �
D.
𝑓𝑓�2 � > 𝑓𝑓�2 � > 𝑓𝑓�log2 3�
2 3 2 3
1 −3 −2 −3 −2 1
7.已 𝑓𝑓 知 �l 圆 og 2 3� > 𝑓𝑓�2 � > 𝑓𝑓�2 与 � 圆 𝑓𝑓�2 � > 相 𝑓𝑓 交 �2 于 � 、 > 𝑓𝑓� l 两 og 点 2 ,3 � 直线 交 轴
2 2 2 2
于点 , 则C1 :𝑥𝑥 +(𝑦𝑦 的−最3)小=值8为 C2:(𝑥𝑥−𝑎𝑎) +𝑦𝑦 = 8 A B AB 𝑥𝑥
P
𝑆𝑆△𝐶𝐶1𝑃𝑃𝐶𝐶2
A. B. C. D.
3 9 27 √23
8.若2数列 2的通项公式为 2 , 记2 在数列 的前 项中任取两数
𝑛𝑛−1 ∗
都是正数的 {𝑎𝑎 概𝑛𝑛} 率为 , 则 𝑎𝑎𝑛𝑛 = (−1) 𝑛𝑛 {𝑎𝑎𝑛𝑛} 𝑛𝑛+2(𝑛𝑛 ∈ 𝑁𝑁 )
A. 𝑃𝑃B𝑛𝑛. C. D.
2
二、𝑃𝑃1选=择3题: 本题共 3 𝑃𝑃小9 <题𝑃𝑃,1 0每小题 6 分𝑃𝑃,1 0共< 𝑃𝑃1181 分. 在每小𝑃𝑃1题1 <给𝑃𝑃出12的选项中, 有多项符合题目
要求. 全部选对的得 6 分, 部分选对的得部分分, 有选错的得 0 分.
1 / 4
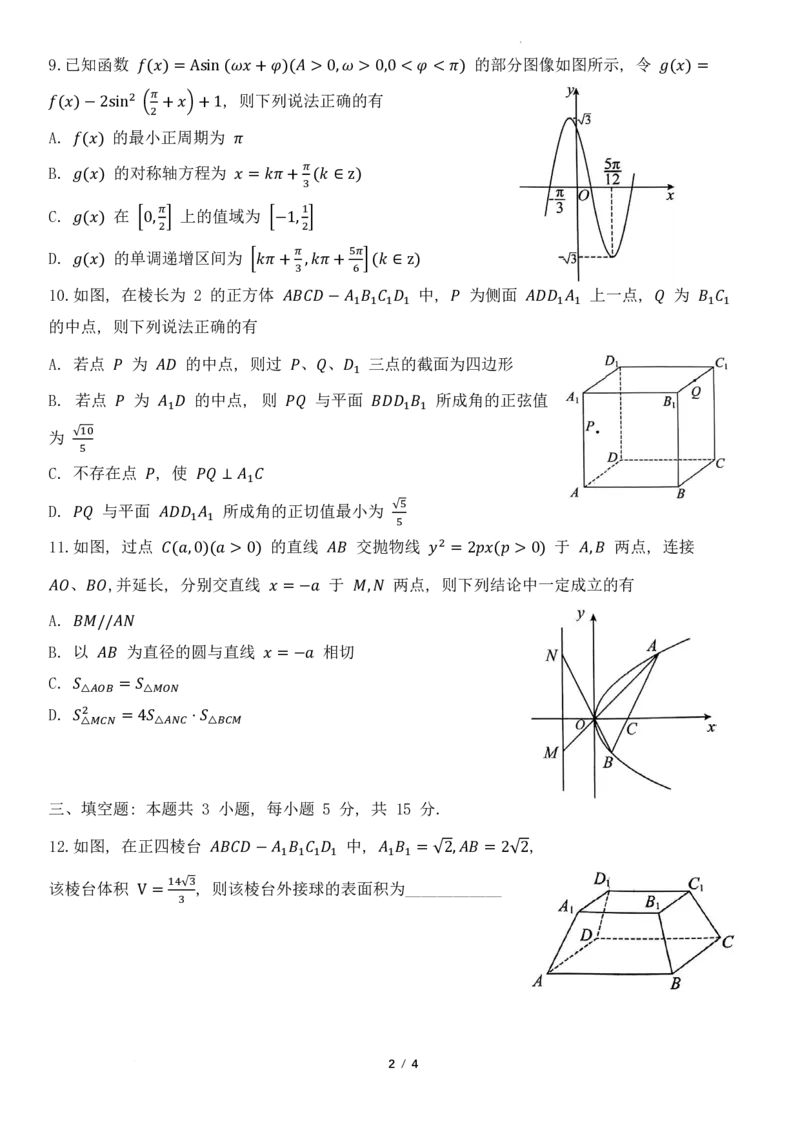
学科网(北京)股份有限公司9.已知函数 的部分图像如图所示, 令
𝑓𝑓(𝑥𝑥) = Asin ,( 𝜔𝜔则𝑥𝑥下+𝜑𝜑列)说(𝐴𝐴法>正0确,𝜔𝜔的>有0 ,0 < 𝜑𝜑 < 𝜋𝜋) 𝑔𝑔(𝑥𝑥) =
2 𝜋𝜋
A𝑓𝑓.( 𝑥𝑥)−2 s的in最 �小2正+周𝑥𝑥�期+为1
B. 𝑓𝑓(𝑥𝑥) 的对称轴方程为 𝜋𝜋
𝜋𝜋
𝑔𝑔(𝑥𝑥) 𝑥𝑥 = 𝑘𝑘𝜋𝜋+ 3(𝑘𝑘 ∈ z)
C. 在 上的值域为
𝜋𝜋 1
D.
𝑔𝑔(𝑥𝑥)
的单
�0
调
,2递 �
增区间为
�−1,2�
𝜋𝜋 5𝜋𝜋
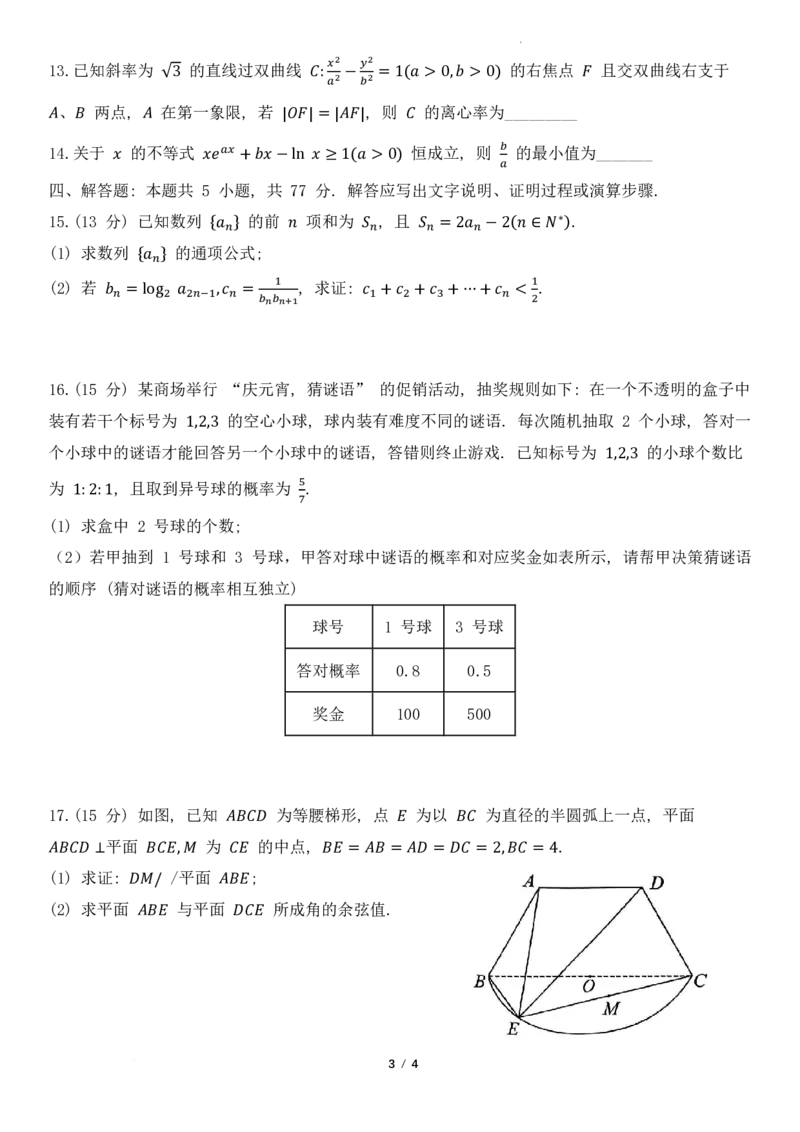
10.𝑔𝑔如(图𝑥𝑥), 在棱长为 2 的正方�𝑘𝑘体𝜋𝜋 + 3,𝑘𝑘𝜋𝜋+ 6�(𝑘𝑘 ∈ z )中, 为侧面 上一点, 为
的中点, 则下列说法正确的有 𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴−𝐴𝐴1𝐵𝐵1𝐴𝐴1𝐴𝐴1 𝑃𝑃 𝐴𝐴𝐴𝐴𝐴𝐴1𝐴𝐴1 𝑄𝑄 𝐵𝐵1𝐴𝐴1
A. 若点 为 的中点, 则过 、 、 三点的截面为四边形
B. 若点 𝑃𝑃 为 𝐴𝐴𝐴𝐴 的中点, 则 𝑃𝑃 与𝑄𝑄平𝐴𝐴面1 所成角的正弦值
为 𝑃𝑃 𝐴𝐴1𝐴𝐴 𝑃𝑃𝑄𝑄 𝐵𝐵𝐴𝐴𝐴𝐴1𝐵𝐵1
√10
C. 不5存在点 , 使
D. 与平面𝑃𝑃 𝑃𝑃𝑄𝑄 ⊥所𝐴𝐴成 1𝐴𝐴角的正切值最小为
√5
11.𝑃𝑃如𝑄𝑄图, 过点 𝐴𝐴𝐴𝐴𝐴𝐴1𝐴𝐴1 的直线 交抛物5线 于 两点, 连接
2
、 ,并延长𝐴𝐴,( 𝑎𝑎分,0别)(交𝑎𝑎直>线0) 𝐴𝐴于𝐵𝐵 两点,𝑦𝑦 则=下2列𝑝𝑝𝑥𝑥结(𝑝𝑝论>中0一) 定成𝐴𝐴立,𝐵𝐵的有
𝐴𝐴A.𝐴𝐴 𝐵𝐵𝐴𝐴 𝑥𝑥 = − 𝑎𝑎 𝑀𝑀,𝑁𝑁
B. 以 为直径的圆与直线 相切
𝐵𝐵𝑀𝑀//𝐴𝐴𝑁𝑁
C.
𝐴𝐴𝐵𝐵 𝑥𝑥 = −𝑎𝑎
D. 𝑆𝑆△𝐴𝐴𝐴𝐴𝐴𝐴 = 𝑆𝑆△𝑀𝑀𝐴𝐴𝑀𝑀
2
𝑆𝑆△𝑀𝑀𝐶𝐶𝑀𝑀 = 4𝑆𝑆△𝐴𝐴𝑀𝑀𝐶𝐶 ⋅𝑆𝑆△𝐴𝐴𝐶𝐶𝑀𝑀
三、填空题: 本题共 3 小题, 每小题 5 分, 共 15 分.
12.如图, 在正四棱台 中, ,
𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴−𝐴𝐴1𝐵𝐵1𝐴𝐴1𝐴𝐴1 𝐴𝐴1𝐵𝐵1 = √2,𝐴𝐴𝐵𝐵 = 2√2
该棱台体积 , 则该棱台外接球的表面积为____________
14√3
V = 3
2 / 4
学科网(北京)股份有限公司13.已知斜率为 的直线过双曲线 的右焦点 且交双曲线右支于
2 2
𝑥𝑥 𝑦𝑦
2 2
、 两点,
在√3
第一象限, 若
𝐴𝐴:𝑎𝑎 −𝑏𝑏, =
则
1 (𝑎𝑎
的
>
离
0,𝑏𝑏
心
>
率
0
为
)
_________
𝐹𝐹
𝐴𝐴14.关𝐵𝐵于 的𝐴𝐴不等式 |𝐴𝐴𝐹𝐹| = |𝐴𝐴𝐹𝐹| 𝐴𝐴恒成立, 则 的最小值为_______
𝑎𝑎𝑥𝑥 𝑏𝑏
四、解答𝑥𝑥题: 本题共 5𝑥𝑥 𝑒𝑒小题+,𝑏𝑏 𝑥𝑥共− 7ln7 𝑥𝑥分≥. 1解(𝑎𝑎答>应0写) 出文字说明、𝑎𝑎证明过程或演算步骤.
15.(13 分) 已知数列 的前 项和为 , 且 .
∗
(1) 求数列 的通项 {𝑎𝑎 公𝑛𝑛} 式; 𝑛𝑛 𝑆𝑆𝑛𝑛 𝑆𝑆𝑛𝑛 = 2𝑎𝑎𝑛𝑛 −2(𝑛𝑛 ∈ 𝑁𝑁 )
(2) 若 {𝑎𝑎𝑛𝑛} , 求证: .
1 1
𝑏𝑏𝑛𝑛 = log2 𝑎𝑎2𝑛𝑛−1,𝑐𝑐𝑛𝑛 = 𝑏𝑏𝑛𝑛𝑏𝑏𝑛𝑛+1 𝑐𝑐1 +𝑐𝑐2 +𝑐𝑐3 +⋯+𝑐𝑐𝑛𝑛 < 2
16.(15 分) 某商场举行 “庆元宵, 猜谜语” 的促销活动, 抽奖规则如下: 在一个不透明的盒子中
装有若干个标号为 的空心小球, 球内装有难度不同的谜语. 每次随机抽取 2 个小球, 答对一
个小球中的谜语才能回答另一个小球中的谜语, 答错则终止游戏. 已知标号为 的小球个数比
1,2,3
为 , 且取到异号球的概率为 . 1,2,3
5
(1)1 求:2盒:1中 2 号球的个数; 7
(2)若甲抽到 1 号球和 3 号球,甲答对球中谜语的概率和对应奖金如表所示, 请帮甲决策猜谜语
的顺序 (猜对谜语的概率相互独立)
球号 1 号球 3 号球
答对概率 0.8 0.5
奖金 100 500
17.(15 分) 如图, 已知 为等腰梯形, 点 为以 为直径的半圆弧上一点, 平面
平面 为 的中点, .
𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴 𝐸𝐸 𝐵𝐵𝐴𝐴
(1) 求证: /平面 ;
𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴 ⊥ 𝐵𝐵𝐴𝐴𝐸𝐸,𝑀𝑀 𝐴𝐴𝐸𝐸 𝐵𝐵𝐸𝐸 = 𝐴𝐴𝐵𝐵 = 𝐴𝐴𝐴𝐴 = 𝐴𝐴𝐴𝐴 = 2,𝐵𝐵𝐴𝐴 = 4
(2) 求平面 与平面 所成角的余弦值.
𝐴𝐴𝑀𝑀/ 𝐴𝐴𝐵𝐵𝐸𝐸
𝐴𝐴𝐵𝐵𝐸𝐸 𝐴𝐴𝐴𝐴𝐸𝐸
3 / 4
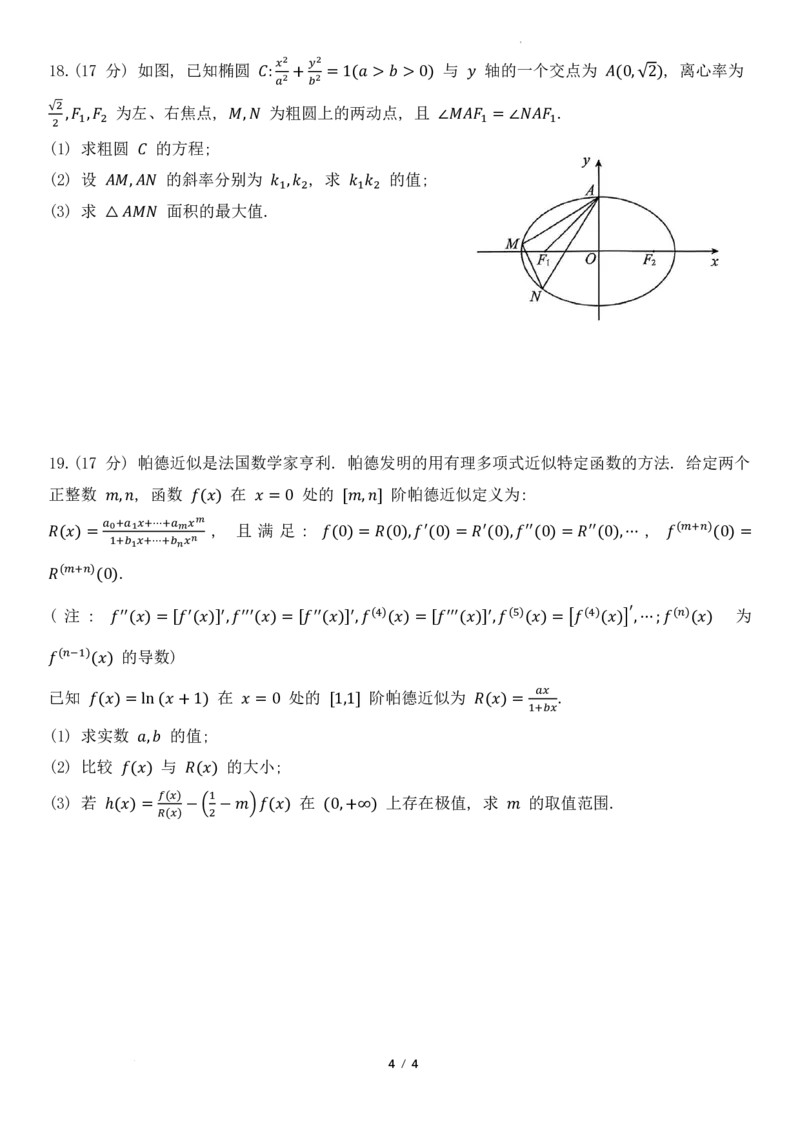
学科网(北京)股份有限公司18.(17 分) 如图, 已知椭圆 与 轴的一个交点为 , 离心率为
2 2
𝑥𝑥 𝑦𝑦
2 2
为左、右焦点, 𝐴𝐴 : 为𝑎𝑎粗 + 圆𝑏𝑏上 = 的 1 两 (𝑎𝑎 动 > 点 𝑏𝑏 , > 且 0) 𝑦𝑦 . 𝐴𝐴(0,√2)
√2
(21),𝐹𝐹 1求,𝐹𝐹粗2 圆 的方程; 𝑀𝑀,𝑁𝑁 ∠𝑀𝑀𝐴𝐴𝐹𝐹1 = ∠𝑁𝑁𝐴𝐴𝐹𝐹1
(2) 设 的斜率分别为 , 求 的值;
𝐴𝐴
(3) 求 𝐴𝐴𝑀𝑀,𝐴𝐴𝑁𝑁 面积的最大值. 𝑘𝑘 1,𝑘𝑘2 𝑘𝑘1𝑘𝑘2
△𝐴𝐴𝑀𝑀𝑁𝑁
19.(17 分) 帕德近似是法国数学家亨利. 帕德发明的用有理多项式近似特定函数的方法. 给定两个
正整数 , 函数 在 处的 阶帕德近似定义为:
𝑚𝑚,𝑛𝑛 𝑓𝑓(𝑥𝑥,) 且𝑥𝑥满=足0 : [𝑚𝑚,𝑛𝑛] ,
𝑚𝑚
𝑎𝑎0+𝑎𝑎1𝑥𝑥+⋯+𝑎𝑎𝑚𝑚𝑥𝑥
′ ′ ′′ ′′ (𝑚𝑚+𝑛𝑛)
𝑛𝑛
𝑅𝑅(𝑥𝑥) = 1+.𝑏𝑏 1𝑥𝑥+⋯+𝑏𝑏𝑛𝑛𝑥𝑥 𝑓𝑓(0) = 𝑅𝑅(0),𝑓𝑓 (0) = 𝑅𝑅 (0),𝑓𝑓 (0) = 𝑅𝑅 (0),⋯ 𝑓𝑓 (0) =
(𝑚𝑚+𝑛𝑛)
𝑅𝑅 (0)
( 注 : 为
′
′′ ′ ′ ′′′ ′′ ′ (4) ′′′ ′ (5) (4) (𝑛𝑛)
𝑓𝑓 的(𝑥𝑥导)数=)[ 𝑓𝑓 (𝑥𝑥)] ,𝑓𝑓 (𝑥𝑥) = [𝑓𝑓 (𝑥𝑥)] ,𝑓𝑓 (𝑥𝑥) = [𝑓𝑓 (𝑥𝑥)] ,𝑓𝑓 (𝑥𝑥) = �𝑓𝑓 (𝑥𝑥)� ,⋯;𝑓𝑓 (𝑥𝑥)
(𝑛𝑛−1)
已𝑓𝑓 知 (𝑥𝑥) 在 处的 阶帕德近似为 .
𝑎𝑎𝑥𝑥
(1) 求𝑓𝑓实(𝑥𝑥数) = ln ( 𝑥𝑥的+值1;) 𝑥𝑥 = 0 [1,1] 𝑅𝑅(𝑥𝑥) = 1+𝑏𝑏𝑥𝑥
(2) 比较 与 的大小;
𝑎𝑎,𝑏𝑏
(3) 若 𝑓𝑓(𝑥𝑥) 𝑅𝑅(𝑥𝑥) 在 上存在极值, 求 的取值范围.
𝑓𝑓(𝑥𝑥) 1
ℎ(𝑥𝑥) = 𝑅𝑅(𝑥𝑥)−�2−𝑚𝑚�𝑓𝑓(𝑥𝑥) (0,+∞) 𝑚𝑚
4 / 4
学科网(北京)股份有限公司