2024年高三一模考试数学试题_2024年3月_013月合集_2024届山东省菏泽市高三一模考试_山东省菏泽市2024届高三一模考试数学

2024 年高三一模考试 数学试题 一、选择题: 本题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项是 符合题目要求的. 1.已知样本数据为 x 、x 、x 、x 、x 、x 、x , 去掉一个最大值和一个最小值后的数据与原来 1 2 3 4 5 6 7 的数据相比, 下列数字特征一定不变的是 A. 极差 B. 平均数 C. 中位数 D. 方差 2.已知复数 满足 , 其中 为虚数单位, 则 的虚部为 z z(1+i)=i2024 i z 1 1 1 ❑√2 A. - B. C. - i D. 2 2 2 2 3.已知集合 A={x∣x=3n,n∈Z},B={x∣0≤x≤6}, 则 A∩B= A. {1,2} B. {3,6} C. {0,1,2} D. {0,3,6} 4. 的展开式中 项的系数等于 40 , 则 是 的 p:m=2,q:(mx+ y) 5 x2y3 p q A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件 5.已知向量 a=(sin⁡θ,cos⁡θ),b=(❑√2,1), 若 a⋅b=|b|, 则 tan⁡θ= ❑√2 ❑√3 A. B. ❑√2 C. ❑√3 D. 2 2 6.已知 f(x)=xh(x), 其中 h(x) 是奇函数且在 R 上为增函数, 则 A. f ( log ⁡ 1) >f ( 2 - 3 2 ) >f ( 2 - 3 2) B. f ( 2 - 3 2 ) >f ( 2 - 3 2) >f ( log ⁡ 1) 2 3 2 3 C. f ( log ⁡ 1) >f ( 2 - 3 2) >f ( 2 - 3 2 ) D. f ( 2 - 3 2) >f ( 2 - 3 2 ) >f ( log ⁡ 1) 2 3 2 3 7.已知圆 与圆 相交于 两点, 直线 交 轴于点 C :x2+(y-3) 2=8 C :(x-a) 2+ y2=8 A、 B AB x 1 2 , 则 的最小值为 P S △C PC 1 2 3 9 27 ❑√23 A. B. C. D. 2 2 2 2 8.若数列 的通项公式为 , 记在数列 的前 项中任取两数都是正 {a } a =(-1) n-1n {a } n+2(n∈N*) n n n 1 / 5 学科网（北京）股份有限公司数的概率为 P , 则 n 2 A. P = B. P

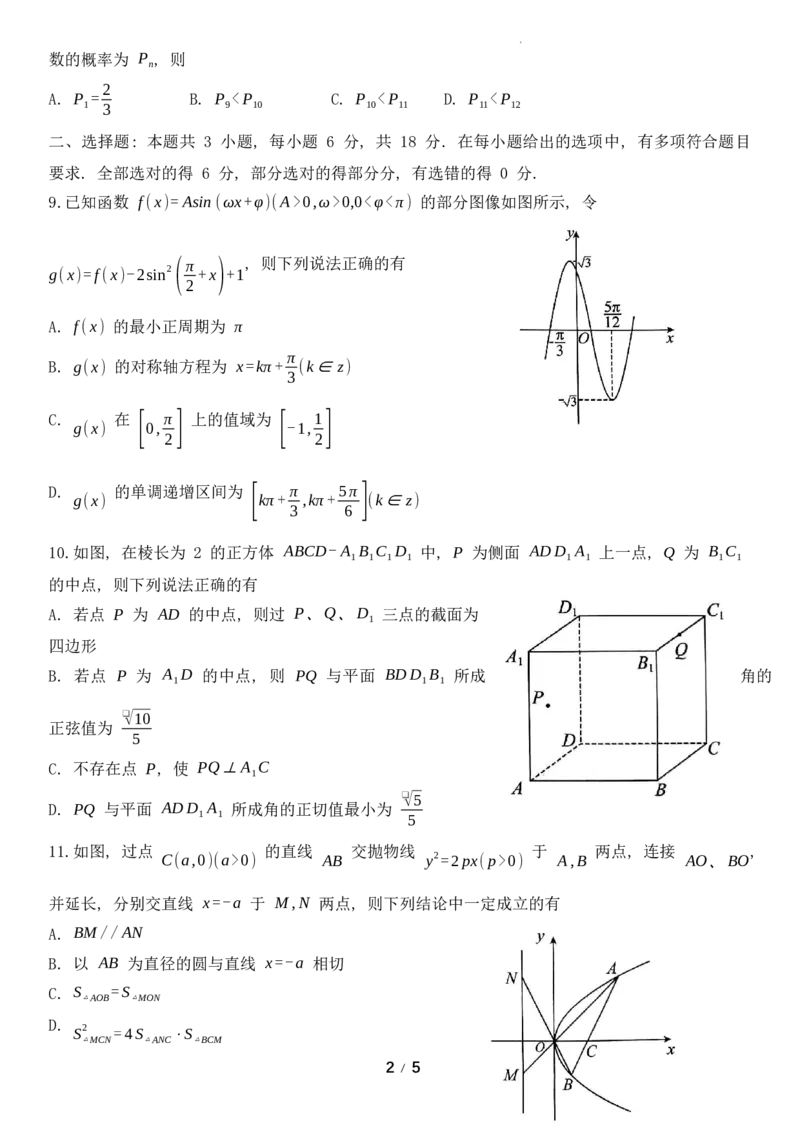
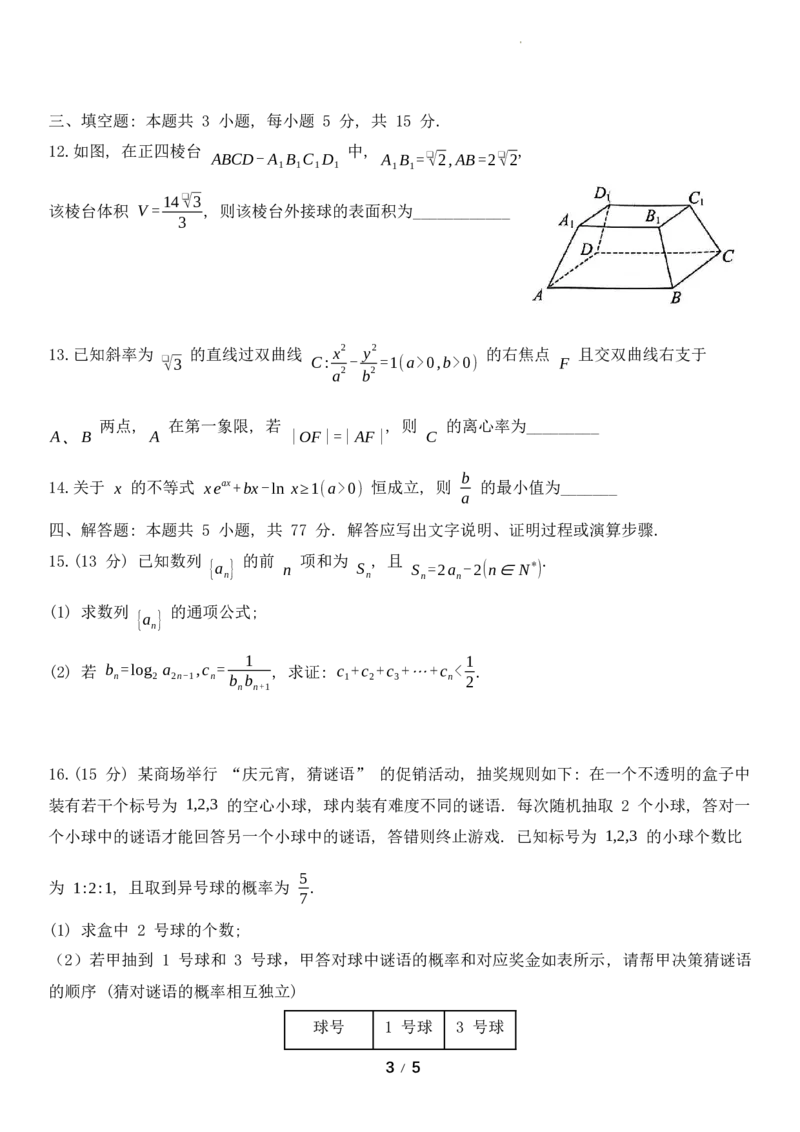
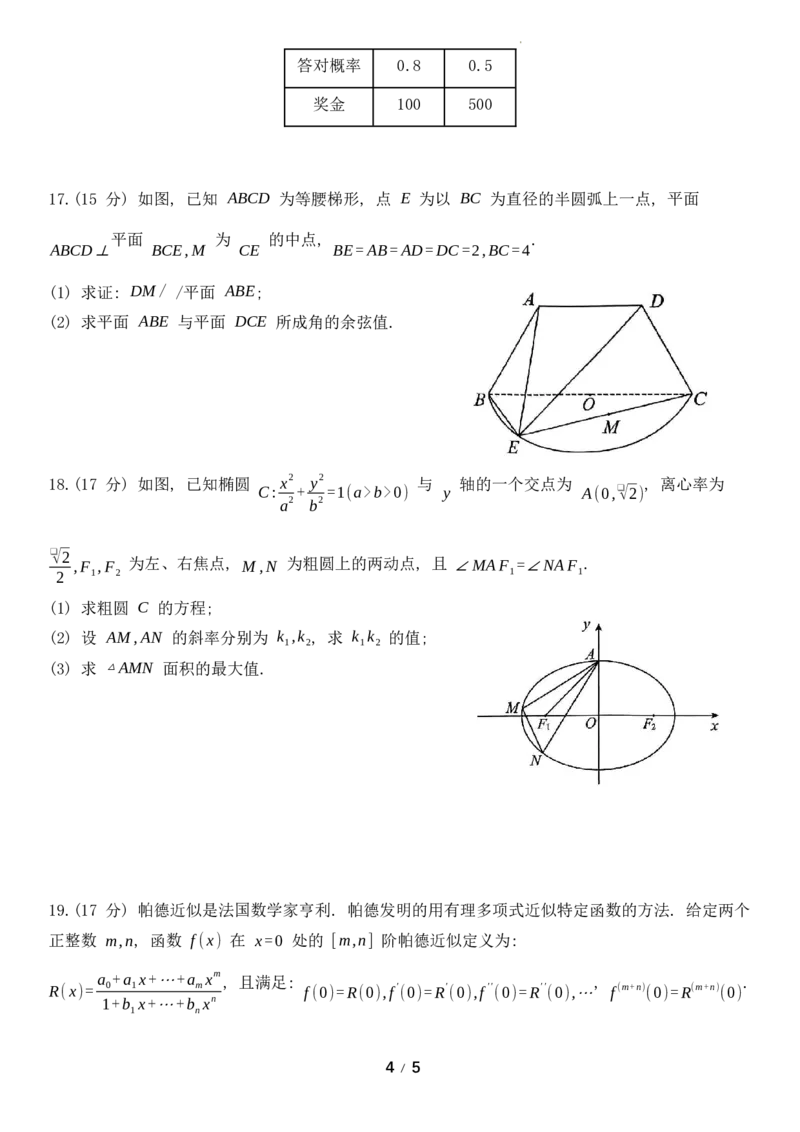
0,ω>0,0<φ<π) 的部分图像如图所示, 令 g(x)=f(x)-2sin2⁡ (π +x ) +1 , 则下列说法正确的有 2 A. f(x) 的最小正周期为 π π B. g(x) 的对称轴方程为 x=kπ+ (k∈z) 3 C. 在 [ π] 上的值域为 [ 1] g(x) 0, -1, 2 2 D. 的单调递增区间为 [ π 5π] g(x) kπ+ ,kπ+ (k∈z) 3 6 10.如图, 在棱长为 2 的正方体 ABCD-A B C D 中, P 为侧面 ADD A 上一点, Q 为 B C 1 1 1 1 1 1 1 1 的中点, 则下列说法正确的有 A. 若点 P 为 AD 的中点, 则过 P、Q、D 三点的截面为 1 四边形 B. 若点 P 为 A D 的中点, 则 PQ 与平面 BDD B 所成 角的 1 1 1 ❑√10 正弦值为 5 C. 不存在点 P, 使 PQ⊥A C 1 ❑√5 D. PQ 与平面 ADD A 所成角的正切值最小为 1 1 5 11.如图, 过点 的直线 交抛物线 于 两点, 连接 , C(a,0)(a>0) AB y2=2px(p>0) A,B AO、BO 并延长, 分别交直线 x=-a 于 M,N 两点, 则下列结论中一定成立的有 A. BM//AN B. 以 AB 为直径的圆与直线 x=-a 相切 C. S =S △AOB △MON D. S2 =4S ⋅S △MCN △ANC △BCM 2 / 5 学科网（北京）股份有限公司三、填空题: 本题共 3 小题, 每小题 5 分, 共 15 分. 12.如图, 在正四棱台 中, , ABCD-A B C D A B =❑√2,AB=2❑√2 1 1 1 1 1 1 14❑√3 该棱台体积 V = , 则该棱台外接球的表面积为____________ 3 13.已知斜率为 的直线过双曲线 x2 y2 的右焦点 且交双曲线右支于 ❑√3 C: - =1(a>0,b>0) F a2 b2 两点, 在第一象限, 若 , 则 的离心率为_________ A、B A |OF|=|AF| C b 14.关于 x 的不等式 xeax+bx-ln⁡x≥1(a>0) 恒成立, 则 的最小值为_______ a 四、解答题: 本题共 5 小题, 共 77 分. 解答应写出文字说明、证明过程或演算步骤. 15.(13 分) 已知数列 的前 项和为 , 且 . {a } n S S =2a -2(n∈N*) n n n n (1) 求数列 的通项公式; {a } n 1 1 (2) 若 b =log ⁡a ,c = , 求证: c +c +c +⋯+c < . n 2 2n-1 n b b 1 2 3 n 2 n n+1 16.(15 分) 某商场举行 “庆元宵, 猜谜语” 的促销活动, 抽奖规则如下: 在一个不透明的盒子中 装有若干个标号为 1,2,3 的空心小球, 球内装有难度不同的谜语. 每次随机抽取 2 个小球, 答对一 个小球中的谜语才能回答另一个小球中的谜语, 答错则终止游戏. 已知标号为 1,2,3 的小球个数比 5 为 1:2:1, 且取到异号球的概率为 . 7 (1) 求盒中 2 号球的个数; （2）若甲抽到 1 号球和 3 号球，甲答对球中谜语的概率和对应奖金如表所示, 请帮甲决策猜谜语 的顺序 (猜对谜语的概率相互独立) 球号 1 号球 3 号球 3 / 5 学科网（北京）股份有限公司答对概率 0.8 0.5 奖金 100 500 17.(15 分) 如图, 已知 ABCD 为等腰梯形, 点 E 为以 BC 为直径的半圆弧上一点, 平面 平面 为 的中点, . ABCD⊥ BCE,M CE BE=AB=AD=DC=2,BC=4 (1) 求证: DM/ /平面 ABE; (2) 求平面 ABE 与平面 DCE 所成角的余弦值. 18.(17 分) 如图, 已知椭圆 x2 y2 与 轴的一个交点为 , 离心率为 C: + =1(a>b>0) y A(0,❑√2) a2 b2 ❑√2 ,F ,F 为左、右焦点, M,N 为粗圆上的两动点, 且 ∠MAF =∠NAF . 2 1 2 1 1 (1) 求粗圆 C 的方程; (2) 设 AM,AN 的斜率分别为 k ,k , 求 k k 的值; 1 2 1 2 (3) 求 △AMN 面积的最大值. 19.(17 分) 帕德近似是法国数学家亨利. 帕德发明的用有理多项式近似特定函数的方法. 给定两个 正整数 m,n, 函数 f(x) 在 x=0 处的 [m,n] 阶帕德近似定义为: a +a x+⋯+a xm , 且满足: , . R(x)= 0 1 m f(0)=R(0),f' (0)=R' (0),f'' (0)=R'' (0),⋯ f(m+n)(0)=R(m+n)(0) 1+b x+⋯+b xn 1 n 4 / 5 学科网（北京）股份有限公司(注: f'' (x)=[f' (x)] ' ,f''' (x)=[f'' (x)] ' ,f(4)(x)=[f''' (x)] ' ,f(5)(x)=[f(4)(x)] ' ,⋯;f(n)(x) 为 f(n-1)(x) 的导 数) ax 已知 f(x)=ln⁡(x+1) 在 x=0 处的 [1,1] 阶帕德近似为 R(x)= . 1+bx (1) 求实数 a,b 的值; (2) 比较 f(x) 与 R(x) 的大小; (3) 若 f(x) (1 ) 在 上存在极值, 求 的取值范围. h(x)= - -m f(x) (0,+∞) m R(x) 2 5 / 5 学科网（北京）股份有限公司