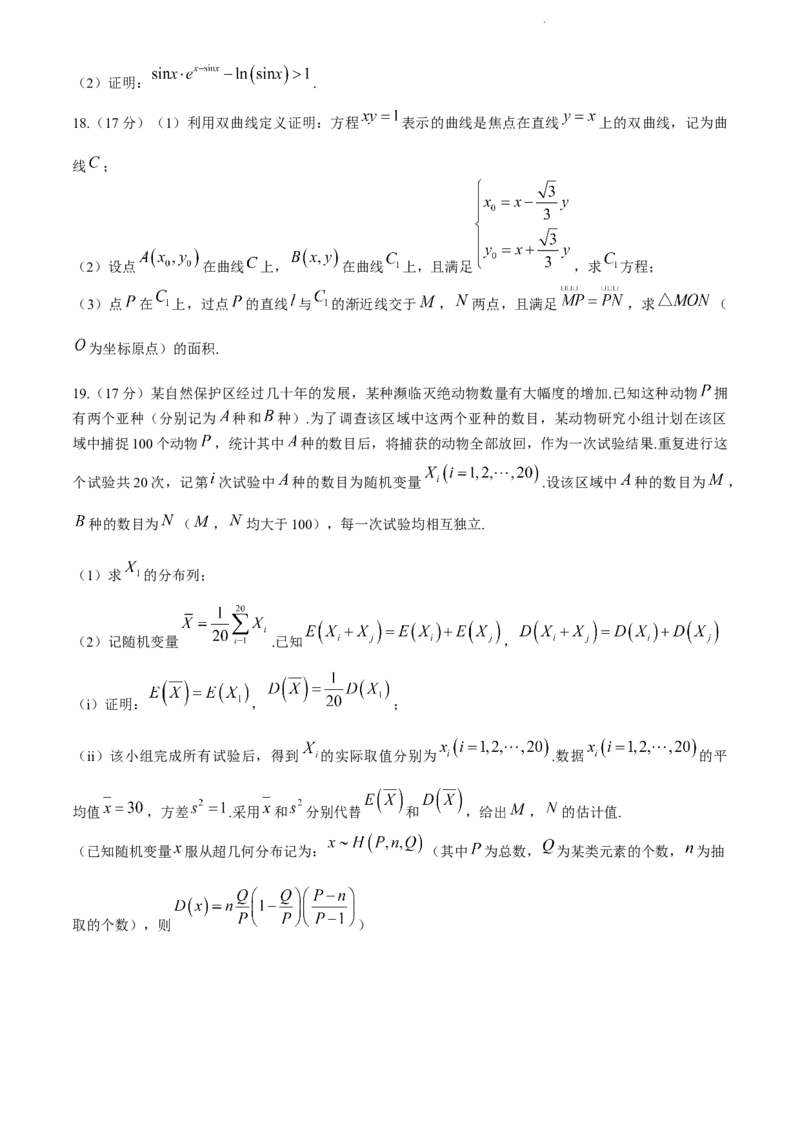文档内容
2023—2024 学年度下学期高三第二次模拟考试试题
数学
命题人:抚顺二中 孙振刚 旅顺中学 王莹
时间:120分钟 试卷满分:150分
注意事项:
1.答题前,考生务必将自己的姓名,准考证号填写在答题卡上。
2.答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。答非选择题时,将答案写在答题卡上。写在本试卷
上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.若复数 为实数,则实数 等于( )
A. B. C. D.2
2.已知集合 . .若 ,则 的取值范围为( )
A. B. C. D.
3.下表为某地春节假期某日游客抽取的100人样本的出行方式统计数据
出行方式 高铁 自驾 飞机 客车
频数 27 16 28 29
某实验点从这批游客中抽取25人,当中选择飞机出行的人数大约为( )
A.8 B.7 C.6 D.4
4.在矩形 中, , 为 中点, 为平面 内一点, .则 的
取值范围为( )
A. B. C. D.
5.数列 中, , , ,则 的值为( )
A. B. C.3 D.
6.已知函数 的定义域为 , 是偶函数, 是奇函数,则 最小值为
学科网(北京)股份有限公司( )
A. B. C. D.
7.某同学笔袋里有10支笔,其中8支黑色,2支红色.被甲同学借走2支.已知甲借走的有一支是红色,则另
一支也是红色的概率为( )
A. B. C. D.
8.已知 是椭圆 上的动点,若动点 到定点 的距离 的最小值为
1,则椭圆 的离心率的取值范围是( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知 ,下列不等式正确的是( )
A. B. C. D.
10.若 的展开式中第4项的二项式系数最大,则二项展开式中的有理项( 项中 是整
数)可以是( )
A.第2项 B.第3项 C.第4项 D.第5项
11.已知正四棱台 的各个顶点都在球 的表面上, , ,
, 是线段 上一点,且 ,下列选项正确的( )
A.当 时,过点 作球 的截面的最小面积
B.当 时,多面体
C. 到平面 距离是2
D. 与平面 的夹角正弦值是
学科网(北京)股份有限公司三、填空题:本题共3小题,每小题5分,共15分
12.过点 与圆 相切的切线方程为________.
13.已知公比 大于1的等比数列 满足 , .设 ,则当 时数列
的前 项和 ________.
14.若集合 , , , 满足 , , 都是 的子集,且 , , 均只有一个元素,
且 ,称( , , )为 的一个“有序子集列”,若 有5个元素,则有多少个“有
序子集列”________.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)在 中,角 , , 所对的边分别为 , , ,已知 , .
(1)求 的值;
(2)若 ,求 的面积.
16.(15 分)如图,已知多面体 的底面 为正方形,四边形 是平行四边形,
, , 是 的中点.
(1)证明: 平面 ;
(2)若 是等边三角形,求直线 与平面 所成角的正弦值.
17.(15分)已知函数 ,
(1)求 的最小值;
学科网(北京)股份有限公司(2)证明: .
18.(17分)(1)利用双曲线定义证明:方程 表示的曲线是焦点在直线 上的双曲线,记为曲
线 ;
(2)设点 在曲线 上, 在曲线 上,且满足 ,求 方程;
(3)点 在 上,过点 的直线 与 的渐近线交于 , 两点,且满足 ,求 (
为坐标原点)的面积.
19.(17分)某自然保护区经过几十年的发展,某种濒临灭绝动物数量有大幅度的增加.已知这种动物 拥
有两个亚种(分别记为 种和 种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区
域中捕捉100个动物 ,统计其中 种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这
个试验共20次,记第 次试验中 种的数目为随机变量 .设该区域中 种的数目为 ,
种的数目为 ( , 均大于100),每一次试验均相互独立.
(1)求 的分布列;
(2)记随机变量 .已知 ,
(i)证明: , ;
(ii)该小组完成所有试验后,得到 的实际取值分别为 .数据 的平
均值 ,方差 .采用 和 分别代替 和 ,给出 , 的估计值.
(已知随机变量 服从超几何分布记为: (其中 为总数, 为某类元素的个数, 为抽
取的个数),则 )
学科网(北京)股份有限公司