文档内容
2024 届高考新结构数学-选择填空强化训练(10)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.某篮球兴趣小组7名学生参加投篮比赛,每人投10个,投中的个数分别为8,5,7,5,8,6,8,
则.这组数据的众数和中位数分别为( ).
A 5,7 B. 6,7 C. 8,5 D. 8,7
【答案】D
【解析】数据由小到大排列为5,5,6,7,8,8,8,
因此,这组数据的众数为8,中位数为7.
故选:D.
2.圆心在 轴上,半径为1,且过点 的圆的方程是( )
A. B.
C. D.
【答案】A
【解析】因为圆心在 轴上,所以可设所求圆的圆心坐标为 ,
则圆的方程为 ,又点 在圆上,
所以 ,解得 ,
所以所求圆的方程为 .
故选:A
3.记 为等差数列 的前 项和,若 ,则 ( )
A. 20 B. 16 C. 14 D. 12
【答案】D
【解析】∵ 是等差数列,
∴ , ,所以 ,
∴公差 ,
∴ ,
∴ ,
故选:D.
4.如图,将正四棱台切割成九个部分,其中一个部分为长方体,四个部分为直三棱柱,四个部分为四
棱锥.已知每个直三棱柱的体积为 ,每个四棱锥的体积为 ,则该正四棱台的体积为( )
A. B. C. D.
【答案】C
【解析】设每个直三棱柱高为 ,每个四棱锥的底面都是正方形,设每个四棱锥的底面边长为 ,设正四棱台的高为 ,因为每个直三棱柱的体积为 ,每个四棱锥的体积为 ,
则 ,可得 ,可得 ,
所以,该正四棱台的体积为 .
故选:C.
5.古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长
的乘积.如图, , 为椭圆 : 的左、右焦点,中心为原点,椭圆 的
面积为 ,直线 上一点 满足 是等腰三角形,且 ,则 的离心率为
( )
A. B. C. D.
【答案】B
【解析】由题可知, ,即 , 是以 为顶角的等腰三角形,
则有: , , ,
所以 ,又因为 ,即 , ,
可得: ,解得 ,故离心率为 .
故选:B.
6.如图,在边长为2的菱形 中, ,点E,F分别在边 , 上,且 ,
若 ,则 ( )A. B. C. 1 D.
【答案】C
【解析】设 ,可得 ,
有 , ,
故
,
又由 ,有 ,解得 , (舍),
故 为边 , 的中点,所以 为等边三角形,故 .
故选:C.
7.如图,在正方体 中, , 是正方形 内部(含边界)的一个动点,
若 ,则三棱锥 外接球的表面积为( )
A. B. C. D.
【答案】A
【解析】若 ,则 为 中点, 为等腰直角三角形,外接圆半径为 ,三
棱锥 外接球的球心到平面 的距离为 ,则外接球的半径为 ,所以三棱锥
外接球的表面积为 ,A选项正确;
故选:A
8.方程 所有正根的和为( )
A. B. C. D.
【答案】C
【解析】 ,令 ,则 ,即 ,
所以 或 ,
当 时,即 ,
所以 ,
因为 ,所以 ,
当 时,即 ,
则 ,
因为 是奇数,所以 也是奇数,不成立;
所以方程所有正根的和为: ,
故选:C
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.函数 的图象如图所示,将其向左平移 个单位长度,得到
的图象,则下列说法正确的是( )
A. B. 函数 的图象关于点 对称
C. 函数 的图象关于直线 对称 D. 函数 在 上单调递减
【答案】ABD
【解析】函数 ,当 ,
此时 , ,因为 ,所以 ,所以 ,故A正确;
,所以 关于点 对称,故B正确;
函数图象向左平移 个单位长度后得到 ,
,当 时, ,所以函数 的图象不关于直线 对
称,故C错误;
,当 时, ,
所以函数 在 上单调递减,故D正确.
故选:ABD
10.已知复数 满足 ,则( )
A. 的实部为
B. 的虚部为
C. 满足: 的复数 对应的点所在区域的面积为
D. 对应的向量与 轴正方向所在向量夹角的正切值为
【答案】AC
【解析】由 ,
则 ,
所以 的实部为 ,虚部为 ,故A正确,B错误;
因为 ,
则 ,设 ,
则 ,即 ,
所以复数 对应的点所在区域是以原点为圆心,1为半径的圆内的区域(包括圆),
则所在区域的面积为 ,故C正确;如图, 对应的向量为 ,
则向量 与 轴正方向所在向量夹角的正切值为 ,故D错误.
故选:AC.
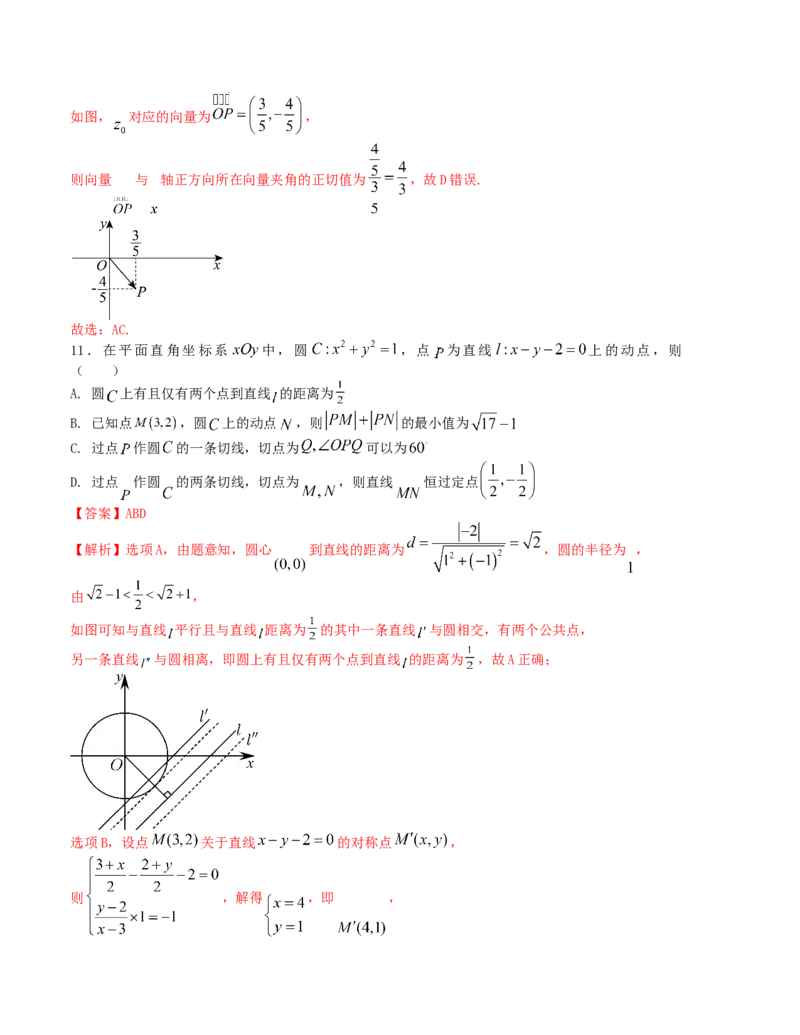
11.在平面直角坐标系 中,圆 ,点 为直线 上的动点,则
( )
A. 圆 上有且仅有两个点到直线 的距离为
B. 已知点 ,圆 上的动点 ,则 的最小值为
C. 过点 作圆 的一条切线,切点为 可以为
D. 过点 作圆 的两条切线,切点为 ,则直线 恒过定点
【答案】ABD
【解析】选项A,由题意知,圆心 到直线的距离为 ,圆的半径为 ,
由 ,
如图可知与直线 平行且与直线 距离为 的其中一条直线 与圆相交,有两个公共点,
另一条直线 与圆相离,即圆上有且仅有两个点到直线 的距离为 ,故A正确;
选项B,设点 关于直线 的对称点 ,
则 ,解得 ,即 ,则 ,
即 的最小值为 ,故B正确;
选项C,由切点为 ,则在 中, ,
当 最小时, 取最大值, 最大,
过点 作 ,垂足为 ,此时 最小,最小值为 ,
即 最大值为 , 最大为 ,不可能为 ,故C错误;
选项D,设点 ,切点 ,
可得切线 方程为 ,由点 在切线上,得 ,
同理可得 ,
故点 都在直线 上,
即直线 的方程为 ,
又由点 在直线 上,则 ,
代入直线方程整理得 ,
由 解得 ,即直线 恒过定点 ,故D正确.
.
故选:ABD三、填空题:本题共3小题,每小题5分,共15分.
12. 的展开式中 的系数为__________.(用数字作答)
【答案】
【解析】 的通项公式为 ,
令 得, ,此时 ,
令 得, ,此时 ,
故 的系数为
故答案为:
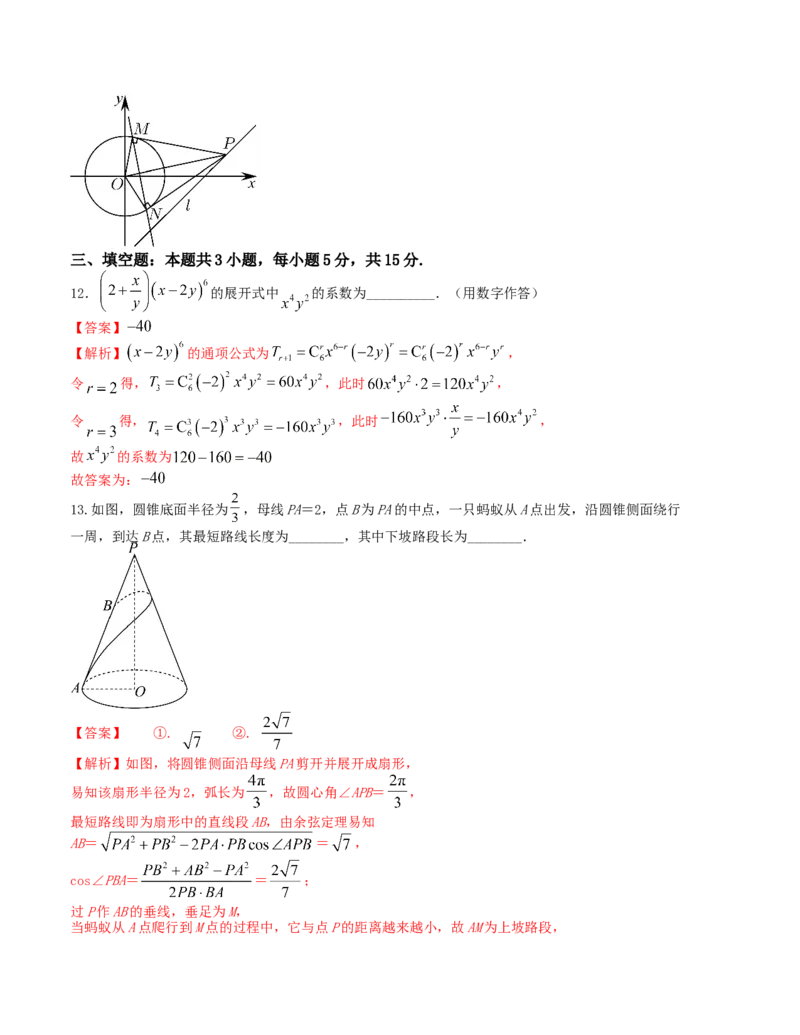
13.如图,圆锥底面半径为 ,母线PA=2,点B为PA的中点,一只蚂蚁从A点出发,沿圆锥侧面绕行
一周,到达B点,其最短路线长度为________,其中下坡路段长为________.
【答案】 ①. ②.
【解析】如图,将圆锥侧面沿母线PA剪开并展开成扇形,
易知该扇形半径为2,弧长为 ,故圆心角∠APB= ,
最短路线即为扇形中的直线段AB,由余弦定理易知
AB= = ,
cos∠PBA= = ;
过P作AB的垂线,垂足为M,
当蚂蚁从A点爬行到M点的过程中,它与点P的距离越来越小,故AM为上坡路段,当蚂蚁从M点爬行到B点的过程中,它与点P的距离越来越大,故MB为下坡路段,
下坡路段长MB=PB・cos∠PBA= .
故答案为: , .
14.设严格递增的整数数列 , ,…, 满足 , .设 为 , ,…,
这19个数中被3整除的项的个数,则 的最大值为________,使得 取到最大值的数列
的个数为________.
【答案】 ①. 18 ②. 25270
【解析】第一个空,设某个数除以 余数为 ,则称该数模 余 ( , 均为整数,且 ),
为了让尽可能多的相邻两数之和被3整除,则要尽量多地出现相邻两数一个模3余1,一个模3余2这
样的组合,这样它们之和才会被3整除.
而 , 均为模3余1,则不可能有19组上述组别,最多出现18组上述组别,
例如严格递增数列1,2,4,5,7,8,10,11,13,14,16,17,19,20,22,23,25,26,28,40,满足题意,
所以 的最大值为18.
第二个空,因为1-40这40个数中,共有27个数符合模3余1或模3余2,则要从这27个数中选出满
足要求的20个数.
第一步,在 到 这20个数中删去一个数(后面再加回来),使得剩下的19个数满足任意两个相邻
数一个模3余1,一个模3余2,这样就形成了18组,即使得 的最大值为18.
第二步,将这27个数从小到大排列,需要删去8个数得到目标19个数的数列.它们中任意相邻两数一
个模3余1,一个模3余2,因此,需要删去的8个数应该为4组相邻的数.
第三步,利用捆绑思想,从27个数中删去4组相邻的数等价于从23个数中删去4个数.有三种情况:
①两端均删去,这种情况不满足要求.因为若两端均删去,那么1和40必定被删去,在下一步加出来
时也最多加回1或40中的一个,而1和40必定在数列中,因此不满足.
②两端均不删去,从中间21个数中选4个数删去,有 种,再从删去的8个数中拿一个加回原来的
19个数中,由 种,共有 种.
③两端中有一个被删去,其余3个数从中间21个数里选,有 种,此时加回来的数必定是删去的
两端之一中的1或40,有1种选法,共 种.
第四步,删去的四组相邻数中有一组中有一个数被加回来,即未被删去,被删去的是这一组中的另一
个数,而对于删去的数,假设为 ,它旁边两个数分别为 ,即排列为 ,在第三步捆绑时,
可能捆绑的组合为 ,然后删去,再补回 ;或者为 ,然后删去,再补回 ,这两种删去方式
结果相同.
综上,共有 种.
故答案为:18;25270