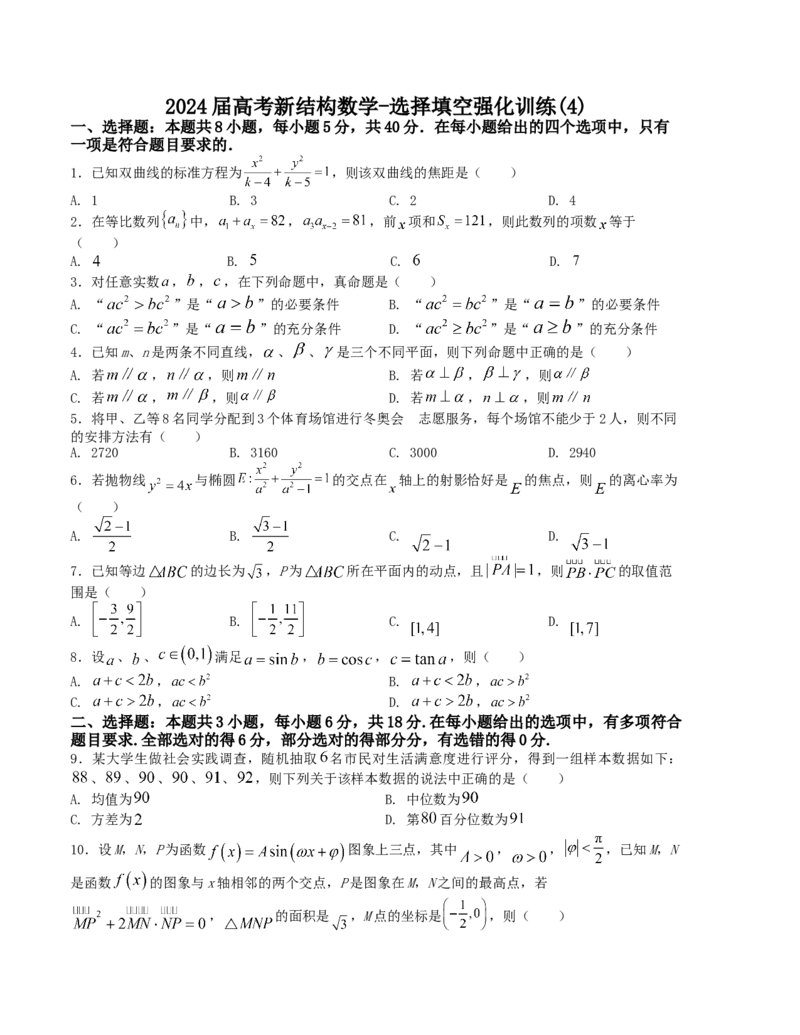文档内容
2024 届高考新结构数学-选择填空强化训练(4)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.已知双曲线的标准方程为 ,则该双曲线的焦距是( )
A. 1 B. 3 C. 2 D. 4
2.在等比数列 中, , ,前 项和 ,则此数列的项数 等于
( )
A. B. C. D.
3.对任意实数 , , ,在下列命题中,真命题是( )
A. “ ”是“ ”的必要条件 B. “ ”是“ ”的必要条件
C. “ ”是“ ”的充分条件 D. “ ”是“ ”的充分条件
4.已知m、n是两条不同直线, 、 、 是三个不同平面,则下列命题中正确的是( )
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
5.将甲、乙等8名同学分配到3个体育场馆进行冬奥会 的志愿服务,每个场馆不能少于2人,则不同
的安排方法有( )
A. 2720 B. 3160 C. 3000 D. 2940
6.若抛物线 与椭圆 的交点在 轴上的射影恰好是 的焦点,则 的离心率为
( )
A. B. C. D.
7.已知等边 的边长为 ,P为 所在平面内的动点,且 ,则 的取值范
围是( )
A. B. C. D.
8.设 、 、 满足 , , ,则( )
A. , B. ,
C. , D. ,
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.某大学生做社会实践调查,随机抽取 名市民对生活满意度进行评分,得到一组样本数据如下:
、 、 、 、 、 ,则下列关于该样本数据的说法中正确的是( )
A. 均值为 B. 中位数为
C. 方差为 D. 第 百分位数为
10.设M,N,P为函数 图象上三点,其中 , , ,已知M,N
是函数 的图象与x轴相邻的两个交点,P是图象在M,N之间的最高点,若
, 的面积是 ,M点的坐标是 ,则( )A. B.
C. D. 函数 在M,N间的图象上存在点Q,使得
11.设a为常数, ,则( ).
A.
B. 成立
.
C
D. 满足条件的 不止一个
三、填空题:本题共3小题,每小题5分,共15分.
12.在复平面内,复数 对应的向量为 ,复数 对应的向量为 ,那么向量
对应的复数是__________.
13.已知轴截面为正三角形的圆锥 的高与球 的直径相等,则圆锥 的体积与球 的体积的
比值是__________,圆锥 的表面积与球 的表面积的比值是__________.
14.方程 的最小的29个非负实数解之和为______.