清远一中2025-2026学年度高三10月期中考试数学试卷_2025年10月_251031广东省清远市第一中学2025-2026学年高三上学期10月期中

清远一中2025-2026学年度高三10月期中考试 数学试卷 一、单选题 1.设抛物线的顶点为O，焦点为F，准线为l.P是抛物线上异于O的一点，过P作PQ⊥l于Q，则 线段FQ的垂直平分线( ) A. 经过点O B. 经过点P C. 平行于直线OP D. 垂直于直线OP 2.设集合 ， ，则 （ ） A. B. C. D. 3.某演讲比赛8位参赛选手的最终得分分别为92，88，95，93，90，97，94，96，其中位数为( ) A. 91.5 B. 93 C. 93.5 D. 94 4.清代的苏州府被称为天下粮仓，大批量的粮食要从苏州府运送到全国各地．为了核准粮食的数 量，苏州府制作了“小嘴大肚”的官斛用以计算粮食的多少，五斗为一斛，而一只官斛的容量恰 好为一斛，其形状近似于正四棱台，上口为正方形，内边长为 25cm，下底也为正方形，内边长为 50cm，斛内高36cm，那么一斗米的体积大约为立方厘米?（ ） A. 10500 B. 12500 C. 31500 D. 52500 5.已知函数 若存在实数x ，x 满足 ，且 ，则 1 2 的最大值为（ ） 1 A. e-1 B. C. D. 1 2 π 2  π sin  sin cos 2      6.已知  3 3 ，则  3 （ ） 5 1 1 5   A. 9 B. 9 C. 9 D. 9 (3π ) 7.已知函数f (x)=Acos(2x+φ)(A>0,|φ|<π)是奇函数，且f =−1，将f (x)的图象上所 4 1 有点的横坐标变为原来的 倍，纵坐标不变，所得图象对应的函数为g(x)，则（ ） 2 π π A. g(x)=sin4x B. g(x)=sinx C. g(x)=cos( 4x+ ) D. g(x)=cos( x+ ) 4 4 8.已知圆锥MO的底面半径为❑√3，高为1，其中O为底面圆心，AB是底面圆的一条直径，若点P 在圆锥MO的侧面上运动，则⃗PA⋅⃗PB的最小值为（ ） 9 3 A. − B. − C. −2 D. −1 4 2 二、多选题 ABCDABC D 2,O 9.已知正方体 1 1 1 1的棱长为 是空间中的一动点，下列结论正确的是（ ） π π ,   A. 若点O在正方形DCC 1 D 1 内部，异面直线A 1 B 1 与OB所成角为θ，则θ的范围为3 2 ABC ACD B. 平面 1 1平面 1  1  C. 若AO 4 ABAD01 ，则B 1 OOD的最小值为 13    AOAB1AD01 OAD ABCDABC D D. 若 ，则平面 1截正方体 1 1 1 1所得截面面积 4 2 的最大值为 C 10.平面上到两定点的距离之积为常数的动点的轨迹称为卡西尼卵形线.已知曲线 是到两定点 F( 2，0)，F ( 2，0) Pm,n C 1 2 的距离之积为常数2的点的轨迹，设 是曲线 上的点，给出下列结 论，其中正确的是（ ）C O 1n1 A. 曲线 关于原点 成中心对称 B. C. S PF 1 F 2 1 D.  PF 1 F 2周长的最小值为 4 2 11.已知直线l:(m+2)x−(m−2)y−4=0，圆C:x2+ y2+4x−6 y+9=0，则（ ） A. l过定点(1,1) B. 圆C与y轴相切 C. 若l与圆C有交点，则m的最大值为0 2 D. 若l平分圆C，则m=− 5 三、填空题 S,A,B,C ABC SA ABC  12.已知点 均在半径为2的球面上， 是边长为3的等边三角形， 平面 ， 则SA________． 13.设双曲线 的左、右焦点分别为F ，F ，过点F 的直线l交双曲线左支于A，B两点， 1 2 1 则|BF|＋|AF|的最小值为__________． 2 2 14.在三棱锥A－BCD中，若AD⊥平面BCD，AB⊥BC，AD＝BD＝2，CD＝4，点A，B，C，D在 同一个球面上，则该球的表面积为________. 四、解答题 S  15.设S n 为数列 a n  的前n项和，已知a 1 1,S 4 10，且   n n 为等差数列. a  （1）求 n 的通项公式；  a ,n为奇数 n  b  1 （2）若 n ,n为偶数，求 的前 项和 .  a a b   n n2 n 2n T 2n 16.高三某班为缓解学生高考压力，班委会决定在周班会课上进行“听音乐，猜歌名”的趣味游戏 比赛，现将全班学生分为9组，每组5人，剩余的学生做裁判．比赛规则如下：比赛共分为两轮， 第一轮比赛中9个小组分三场进行比赛，每场比赛有3个小组参加，在规定的时间内猜对歌名最多 的小组获胜，获胜的三个小组进入第二轮比赛；第二轮进行一场比赛，选出获胜队伍．已知甲、4 3 5 , , 乙、丙3个小组的学生能成功猜对歌名的概率分别为5 4 6． （1）现从甲组中任选一名学生进行歌曲试猜，记 5首歌曲中猜对的歌曲数为X ，求随机变量X 的 数学期望； （2）若从甲、乙、丙3个小组中任选一名学生参加猜歌游戏，求该学生猜对歌曲的概率； （3）若第二轮比赛中丁、戊两组并列第一，则设置以下游戏决定最终获胜的小组，游戏规则如下： 从丁、戊小组中任选一名代表，从装有3个白球和2个红球的不透明的盒子中有放回地随机摸出一 个球，摸出白球记1分，摸出红球记2分，以0分开始计分，恰好获得10分或11分则结束摸球．若 该代表获得10分，则该代表所在小组获得胜利，否则另外一组获得胜利．若该代表来自戊组，试 估计戊组获胜的概率． 17.已知实数x，y满足方程x2＋y2－4x＋1＝0.求： (1) 的最大值和最小值； (2)y－x的最小值； (3)x2＋y2的最大值和最小值． 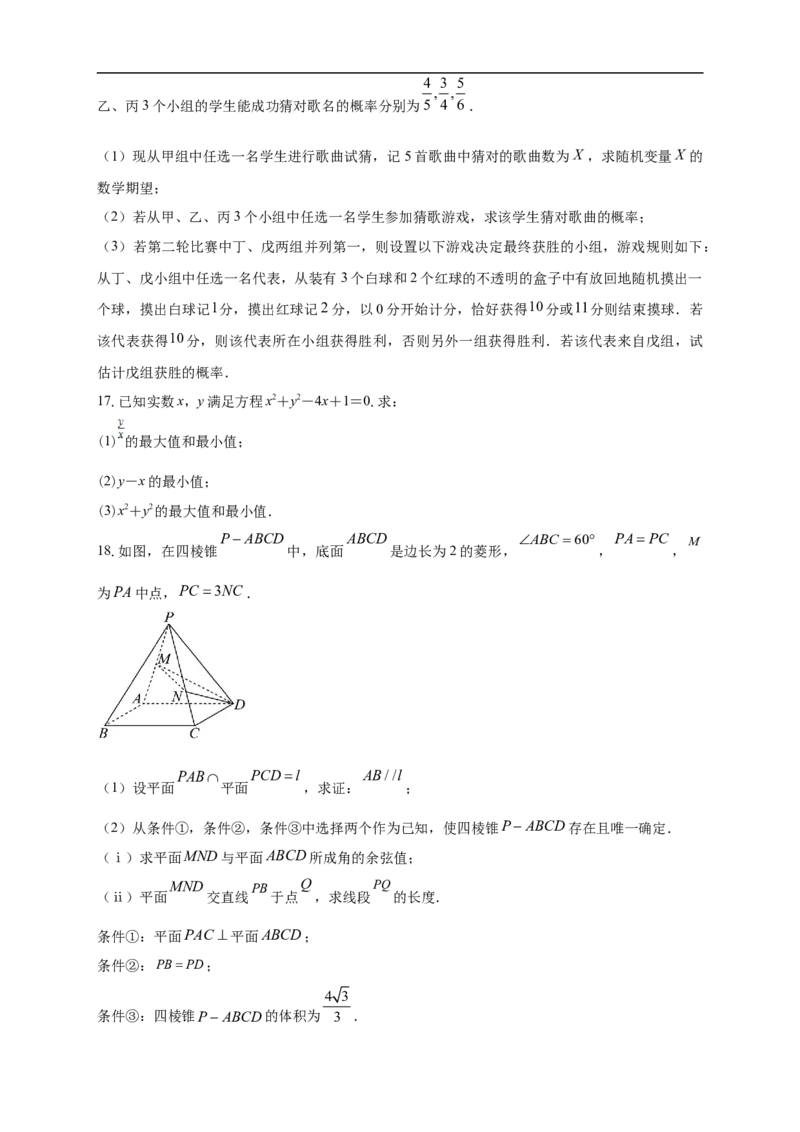PABCD ABCD ABC 60 PAPC M 18.如图，在四棱锥 中，底面 是边长为2的菱形， ， ， 为PA中点，PC 3NC． PAB PCDl AB//l （1）设平面 平面 ，求证： ； （2）从条件①，条件②，条件③中选择两个作为已知，使四棱锥PABCD存在且唯一确定． （ⅰ）求平面MND与平面ABCD所成角的余弦值； MND PB Q PQ （ⅱ）平面 交直线 于点 ，求线段 的长度． 条件①：平面PAC 平面ABCD； 条件②：PBPD； 4 3 条件③：四棱锥PABCD的体积为 3 ．f xx2ex 2ax2 4axa0 19.已知函数 ． y f x 0, f 0 a1 （1）若 ，求曲线 在点 处的切线方程； f x （2）若 恰有三个零点，求a的取值范围．