文档内容
2024 届高考新结构数学-选择填空强化训练(6)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.一组数据按从小到大的顺序排列为2,4,m,12,16,17,若该组数据的中位数是极差的 ,则该
组数据的第40百分位数是( )
A. 4 B. 5 C. 6 D. 9
【答案】C
【解析】根据题意,数据按从小到大的顺序排列为2,4,m,12,16,17,
则极差为 ,故该组数据的中位数是 ,
数据共6个,故中位数为 ,解得 ,
因为 ,所以该组数据的第40百分位数是第3个数6,
故选:C.
2.“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】若 ,则 ,由于 ,所以 ,充分性成立,
当 时, 满足 ,但是 ,必要性不成立,
因此“ ”是“ ”的充分不必要条件
故选:A,
3.已知集合 , ,则 ( )
A. B. C. D.
【答案】A
【解析】】由 ,解得 ,所以 ,
而 ,所以 ,
所以 .故选:A
4.已知 表示两条直线, 表示平面,下列命题中正确的有( )
①若 ,且 ,则 ;
②若 相交且都在平面 外, ,则 ;
③若 ,则 ;
④若 ,且 ,则 .
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A
【解析】对于①,若 ,且 ,则 或相交,故①错误;
对于③和④, 与 也可能相交,均错误;
对于②,设 相交确定平面 ,根据线面平行的判定定理知 ,根据平行平面的传递性
得知 .
故选:A.
5.023年10月23日,杭州亚运会历时16天圆满结束.亚运会结束后,甲、乙、丙、丁、戊五名同学排成
一排合影留念,其中甲、乙均不能站左端,且甲、丙必须相邻,则不同的站法共有( )
A. 18种 B. 24种 C. 30种 D. 36种
【答案】C
【解析】由题意可知,当丙站在左端时,有 种站法;
当丙不站在左端时,有 种站法.
由分类加法计数原理可得,一共有 种不同的站法.
故选:C.
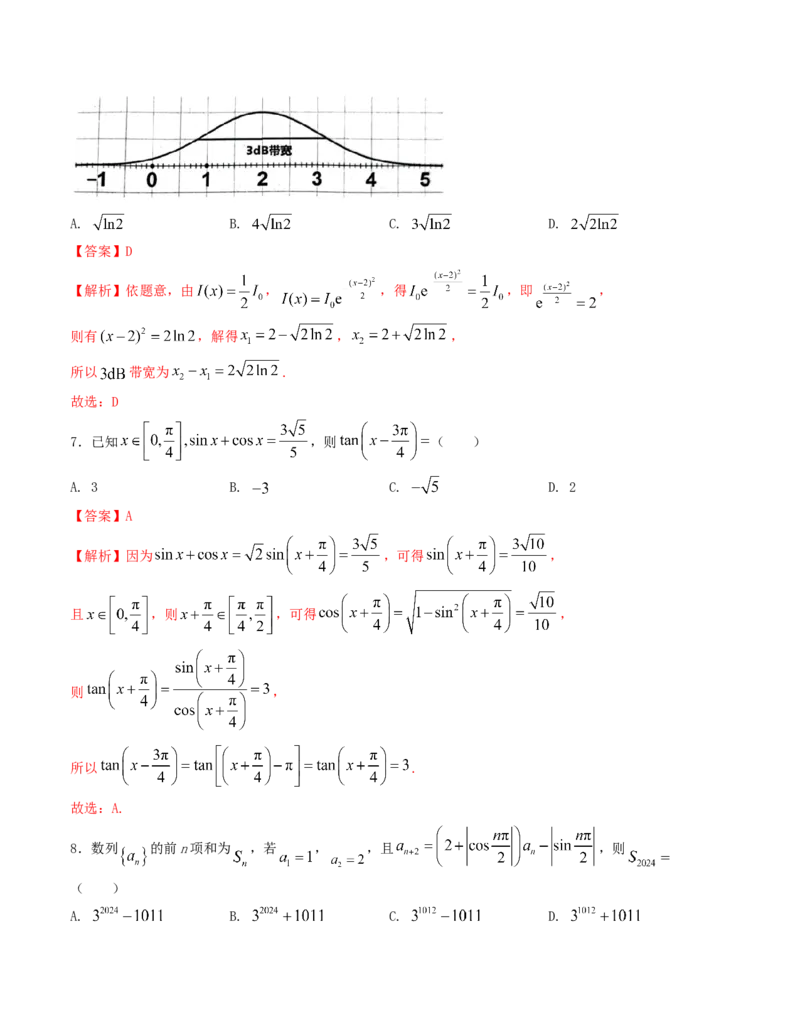
6.一般来说,输出信号功率用高斯函数来描述,定义为 ,其中 为输出信号功率最
大值(单位: ), 为频率(单位: ), 为输出信号功率的数学期望, 为输出信号的
方差, 带宽是光通信中一个常用的指标,是指当输出信号功率下降至最大值一半时,信号的频率
范围,即对应函数图象的宽度。现已知输出信号功率为 (如图所示),则其 带
宽为( )A. B. C. D.
【答案】D
【解析】依题意,由 , ,得 ,即 ,
则有 ,解得 , ,
所以 带宽为 .
故选:D
7.已知 ,则 ( )
A. 3 B. C. D. 2
【答案】A
【解析】因为 ,可得 ,
且 ,则 ,可得 ,
则 ,
所以 .
故选:A.
8.数列 的前n项和为 ,若 , ,且 ,则
( )
A. B. C. D.【答案】D
【解析】令 ,则 ,
即 ,即数列 的所有偶数项构成首项为 ,公比为3的等比数列,
令 ,则 ,
即 ,由于 ,则 ,
故
,
故选:D
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
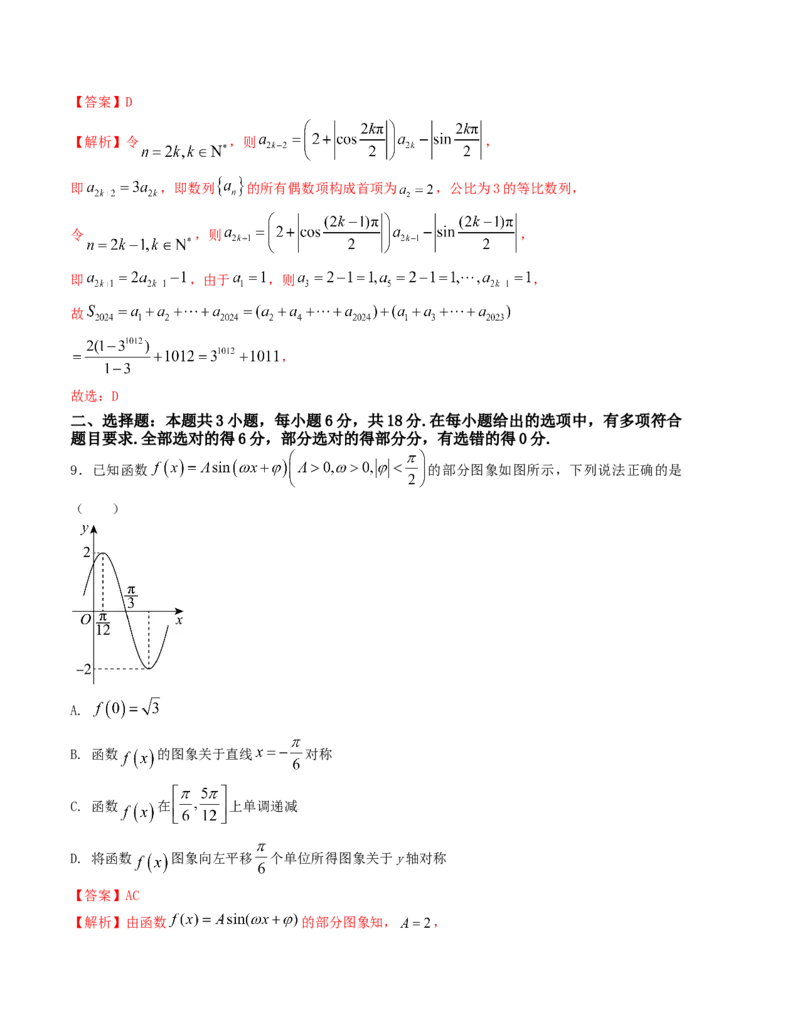
9.已知函数 的部分图象如图所示,下列说法正确的是
( )
A.
B. 函数 的图象关于直线 对称
C. 函数 在 上单调递减
D. 将函数 图象向左平移 个单位所得图象关于y轴对称
【答案】AC
【解析】由函数 的部分图象知, ,,所以 ,
又因为 ,
所以 ;
解得
又因为 ,所以 ,
所以 ;
所以 ,选项A正确;
时, ,
所以 的图象不关于 对称,选项B错误;
时 ,函数 单调递减,选项C正确;
函数 图象向左平移 个单位,得 ,所得图象不关于y轴对称,
选项D错误.
故选:AC.
10.已知 , ,且 ,则( )
A. , B.
C. 最大值为4 D. 的最小值为12
【答案】BCD
【解析】对于选项A:由已知得 , ,
则 , .故A错误;对于选项B:令 ,
则 在 单调递减,在 单调递增,
得 ,故B正确;
对于选项C:结合题意可得 ,令 ,
则 在 上单调递增,得 ,故C正确.
对于选项D:设 ,则 ,
当 时, 单调递减,当 时, 单调递增,
所以 .故D正确.
故选:BCD.
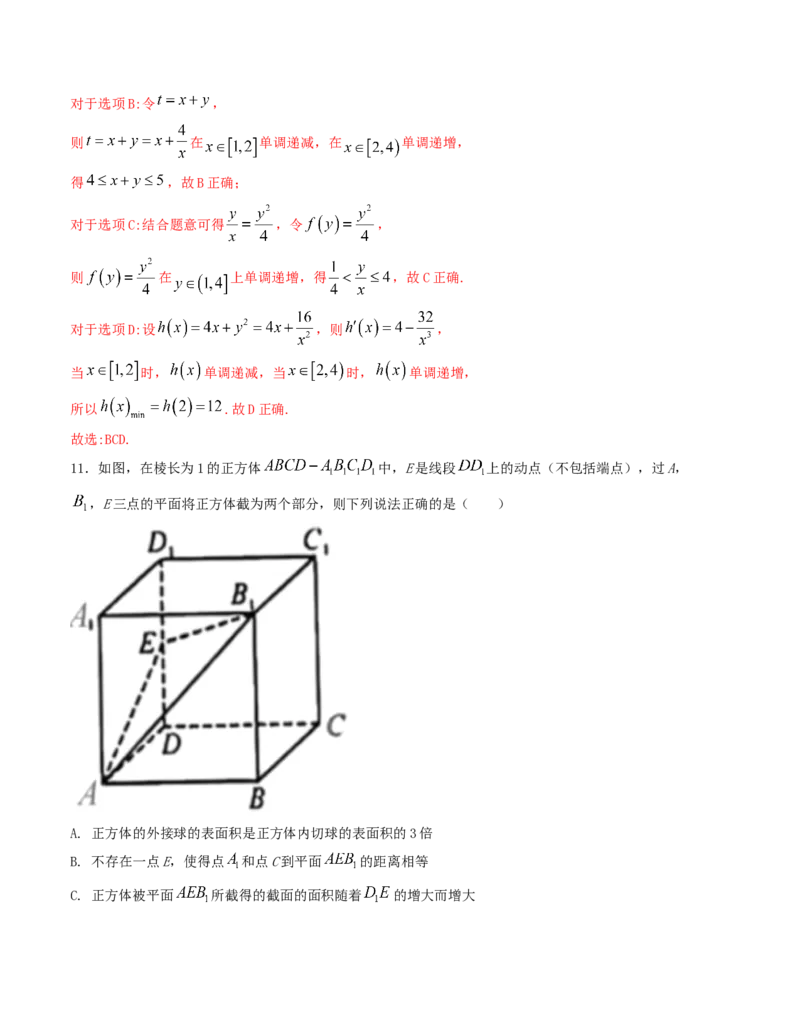
11.如图,在棱长为1的正方体 中,E是线段 上的动点(不包括端点),过A,
,E三点的平面将正方体截为两个部分,则下列说法正确的是( )
A. 正方体的外接球的表面积是正方体内切球的表面积的3倍
B. 不存在一点E,使得点 和点C到平面 的距离相等
C. 正方体被平面 所截得的截面的面积随着 的增大而增大D. 当正方体被平面 所截得的上部分的几何体的体积为 时,E是 的中点
【答案】ABC
【解析】对于A,正方体外接球的半径为 ,内切球的半径为 ,可得正方体的外接球的表面积是正
方体内切球的表面积的 倍,故A正确;
对于B,由点 和点B到平面 的距离相等,若点 和点C到平面 的距离相等,
必有 平面 ,又由 ,可得 平面 ,与 平面 矛盾,
故B正确;
对于C,如图,
在 上取一点F,使得 ,连接 ,设 ,
由 ,可得平面 为过A, ,E三点的截面,
在梯形 中, , , ,
,
梯形 的高为 ,梯形 的面积为
,
令 ,有
.
可得函数 单调递增,可得正方体被平面 所截得的截面面积随着 的增大而增大,
故C正确;
对于D选项, , ,
被平面 所截得的上部分的几何体的体积为 ,整理为 ,
解得 ,故D错误.
故选:ABC
三、填空题:本题共3小题,每小题5分,共15分.
12.设A,B是一个随机试验中的两个零件,若 , , ,则
______.
【答案】
【解析】由 ,有 ,
又由 ,有 ,
可得 .
故答案为:
13.已知 中, , 边上的高与 边上的中线相等,则 __________.
【答案】【解析】如下图所示,设 边上的高为 , 边上的中线为 ,
在 中, ,所以 ,
由 ,平方得 ,
代入得, ,
化简得, ,解得 ,
又因为 ,所以 ,所以 .
故答案为:
14.在同一平面直角坐标系中,P,Q分别是函数 和 图象上的动
点,若对任意 ,有 恒成立,则实数m的最大值为______.
【答案】
【解析】 ,令 , ,
则
当 时 , , 单 调 递 增 , 当 时 , ,
单调递减,
故 在 处取得极小值,也是最小值,故 ,
故 ,当且仅当 时,等号成立,
令 , ,
则 ,令 ,
则 在 上恒成立,
故 在 上单调递增,
又 ,故当 时, ,当 时, ,
故 时, , 单调递减,当 时, , 单调递增,
故 在 处取得极小值,也时最小值,最小值为 ,
设 ,
由基本不等式得,
,
当且仅当 , , 时,等号成立,
故 ,则 .
故答案为: