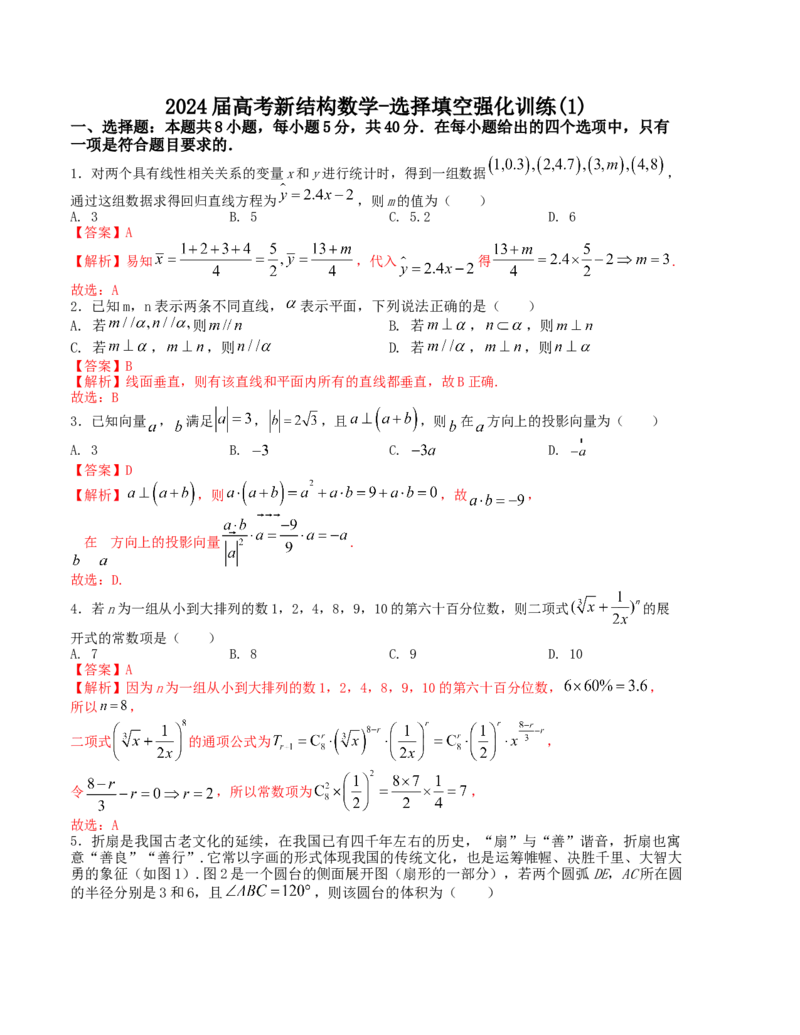文档内容
2024 届高考新结构数学-选择填空强化训练(1)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.对两个具有线性相关关系的变量x和y进行统计时,得到一组数据 ,
通过这组数据求得回归直线方程为 ,则m的值为( )
A. 3 B. 5 C. 5.2 D. 6
【答案】A
【解析】易知 ,代入 得 .
故选:A
2.已知m,n表示两条不同直线, 表示平面,下列说法正确的是( )
A. 若 则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
【答案】B
【解析】线面垂直,则有该直线和平面内所有的直线都垂直,故B正确.
故选:B
3.已知向量 , 满足 , ,且 ,则 在 方向上的投影向量为( )
A. 3 B. C. D.
【答案】D
【解析】 ,则 ,故 ,
在 方向上的投影向量 .
故选:D.
4.若n为一组从小到大排列的数1,2,4,8,9,10的第六十百分位数,则二项式 的展
开式的常数项是( )
A. 7 B. 8 C. 9 D. 10
【答案】A
【解析】因为n为一组从小到大排列的数1,2,4,8,9,10的第六十百分位数, ,
所以 ,
二项式 的通项公式为 ,
令 ,所以常数项为 ,
故选:A
5.折扇是我国古老文化的延续,在我国已有四千年左右的历史,“扇”与“善”谐音,折扇也寓
意“善良”“善行”.它常以字画的形式体现我国的传统文化,也是运筹帷幄、决胜千里、大智大
勇的象征(如图1).图2是一个圆台的侧面展开图(扇形的一部分),若两个圆弧DE,AC所在圆
的半径分别是3和6,且 ,则该圆台的体积为( )A. B. C. D.
【答案】D
【解析】设圆台上下底面的半径分别为 ,由题意可知 ,解得 ,
,解得: ,作出圆台的轴截面,如图所示:
图中 , ,
过点 向 作垂线,垂足为 ,则 ,
所以圆台的高 ,
则上底面面积 , ,由圆台的体积计算公式可得:
,
故选:D.
6.已知函数 的两个零点分别为 ,若 三个数适当调整顺
序后可为等差数列,也可为等比数列,则不等式 的解集为( )
A. B.
C. D.
【答案】A
【解析】由函数 的两个零点分别为 ,
即 是 的两个实数根据,则
因为 ,可得 ,又因为 适当调整可以是等差数列和等比数列,
不妨设 ,可得 ,解得 ,
所以 ,所以 ,
则不等式 ,即为 ,解得 ,所以不等式的解集为 .
故选:A.
7.已知双曲线 : 的左、右焦点分别为 , ,M,N为双曲线一条渐近
线上的两点, 为双曲线的右顶点,若四边形 为矩形,且 ,则双曲线 的离
心率为( )
A. B. C. D.
【答案】C
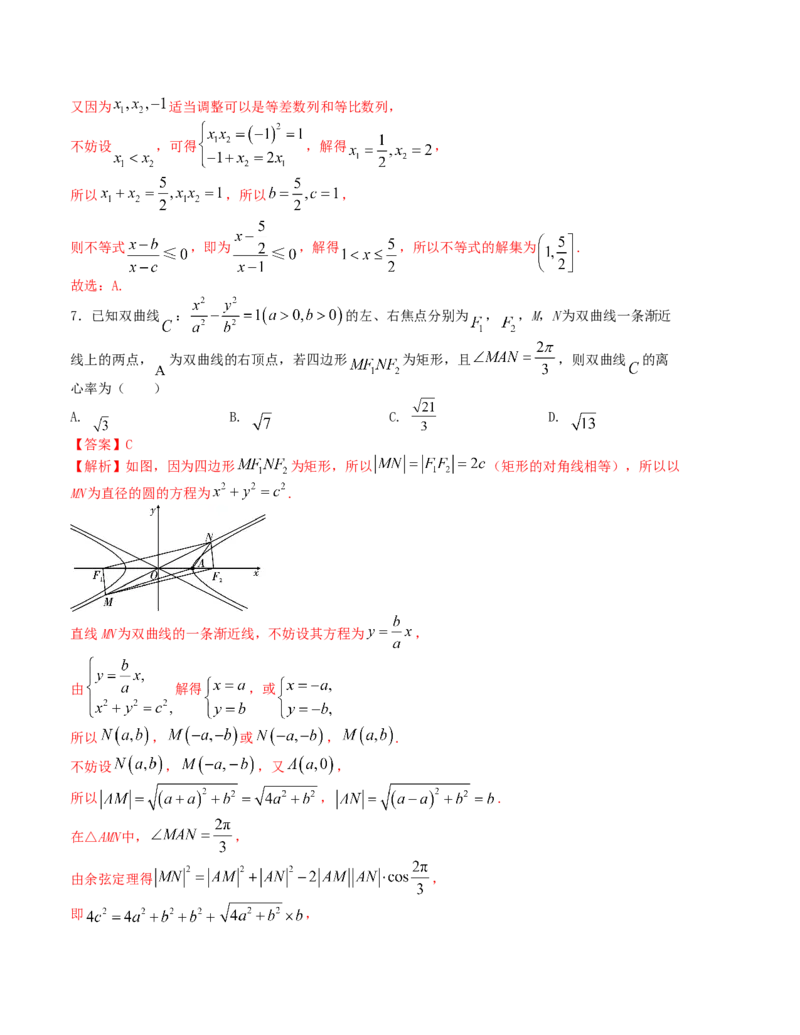
【解析】如图,因为四边形 为矩形,所以 (矩形的对角线相等),所以以
MN为直径的圆的方程为 .
直线MN为双曲线的一条渐近线,不妨设其方程为 ,
由 解得 ,或
所以 , 或 , .
不妨设 , ,又 ,
所以 , .
在△AMN中, ,
由余弦定理得 ,
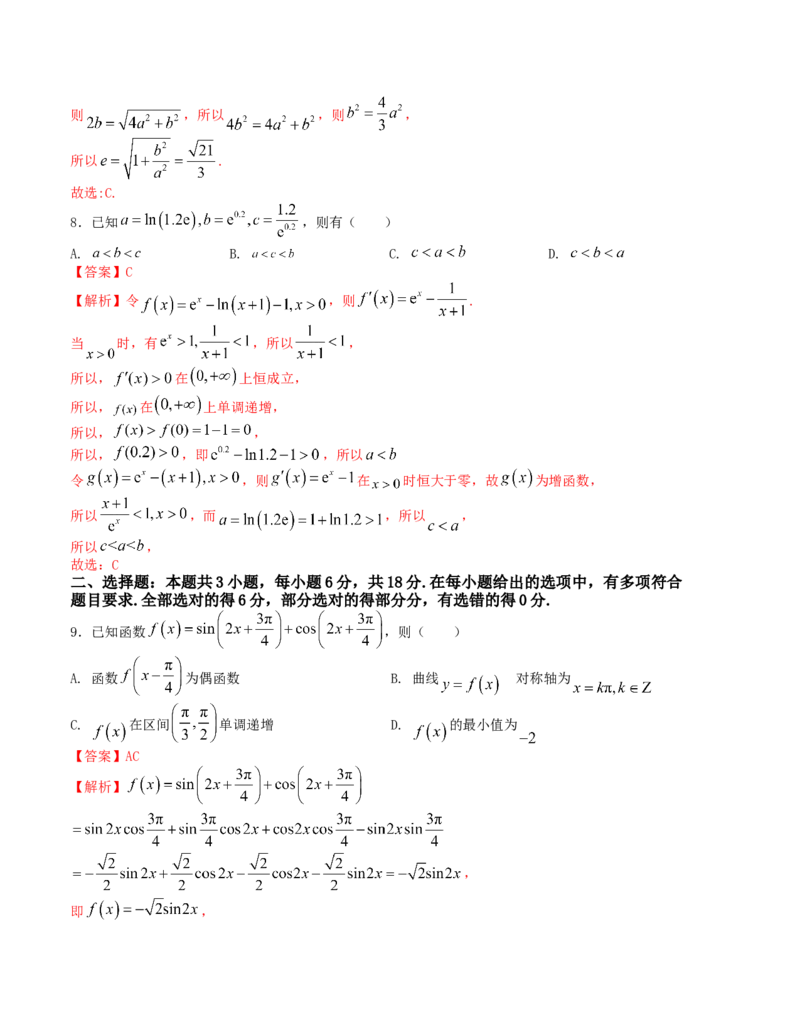
即 ,则 ,所以 ,则 ,
所以 .
故选:C.
8.已知 ,则有( )
A. B. C. D.
【答案】C
【解析】令 ,则 .
当 时,有 ,所以 ,
所以, 在 上恒成立,
所以, 在 上单调递增,
所以, ,
.
所以, ,即 ,所以
令 ,则 在 时恒大于零,故 为增函数,
所以 ,而 ,所以 ,
所以 ,
故选:C
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知函数 ,则( )
A. 函数 为偶函数 B. 曲线 对称轴为
的
C. 在区间 单调递增 D. 的最小值为
【答案】AC
【解析】
,
即 ,对于A, ,易知为偶函数,所以A正确;
对于B, 对称轴为 ,故B错误;
对于C, , 单调递减,则
单调递增,故C正确;
对于D, ,则 ,所以 ,故D错误;
故选:AC
10.设 为复数,则下列命题中正确的是( )
A.
B. 若 ,则复平面内 对应的点位于第二象限
C.
D. 若 ,则 的最大值为2
【答案】ABD
【解析】对于A,设 ,故 ,则 , ,故
成立,故A正确,
对于B, , ,显然复平面内 对应的点位于第二象限,故B正确,
对于C,易知 , ,当 时, ,故C错误,
对于D,若 ,则 ,而 ,易得当 时, 最大,
此时 ,故D正确.
故选:ABD
11.已知菱形 的边长为2, .将 沿着对角线 折起至 ,连结
.设二面角 的大小为 ,则下列说法正确的是( )
A. 若四面体 为正四面体,则
B. 四面体 的体积最大值为1
C. 四面体 的表面积最大值为
D. 当 时,四面体 的外接球的半径为
【答案】BCD
【解析】如图,取 中点 ,连接 ,则 , ,
为二面角 的平面角,即 .若 是正四面体,则 , 不是正三角形, ,A错;
四面体 的体积最大时, 平面 ,此时 到平面 的距离最大为 ,
而 ,所以 ,B正确;
,
易得 , ,
未折叠时 ,折叠到 重合时, ,中间存在一个位置,使得
,则 , ,此时 取得最
大值2,
所以四面体 的表面积最大值为 ,C正确;
当 时,如图,设 分别是 和 的外心,在平面 内作 ,
作 , ,则 是三棱锥外接球的球心,
由上面证明过程知平面 与平面 、平面 垂直,即 四点共面,
,则 , , ,
为球半径,D正确.
故选:BCD.三、填空题:本题共3小题,每小题5分,共15分.
12.设集合 , ,则 ____________.
【答案】
【解析】因为 ,所以 ,即 ,
因为 ,解得 ,所以 ,
所以, .
故答案为:
13.已知正项等比数列 的前 项和为 ,且 ,则 的最小值为
__________.
【答案】
【解析】设正项等比数列 的公比为 ,则 ,
所以,
,
则 ,则 ,可得 ,则 ,
所以,
,
当且仅当 时,即当 时,等号成立,
故 的最小值为 .
故答案为:24
14.已知 为拋物线 的焦点,过点 的直线 与拋物线 交于不同的两点 , ,拋物线
在点 处的切线分别为 和 ,若 和 交于点 ,则 的最小值为__________.
【答案】10
【解析】 的焦点为 ,设直线 方程为 , .
联立直线与抛物线方程有 ,则 .又 求导可得 ,故直线 方程为 .
又 ,故 ,同理 .
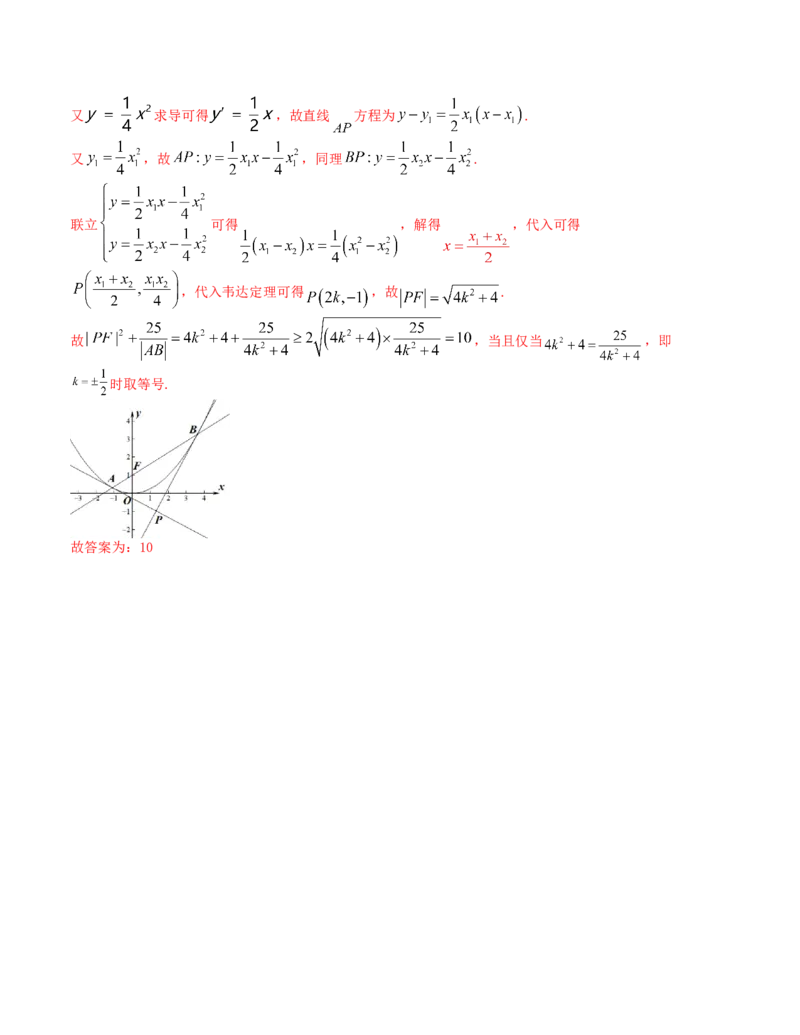
联立 可得 ,解得 ,代入可得
,代入韦达定理可得 ,故 .
故 ,当且仅当 ,即
时取等号.
故答案为:10