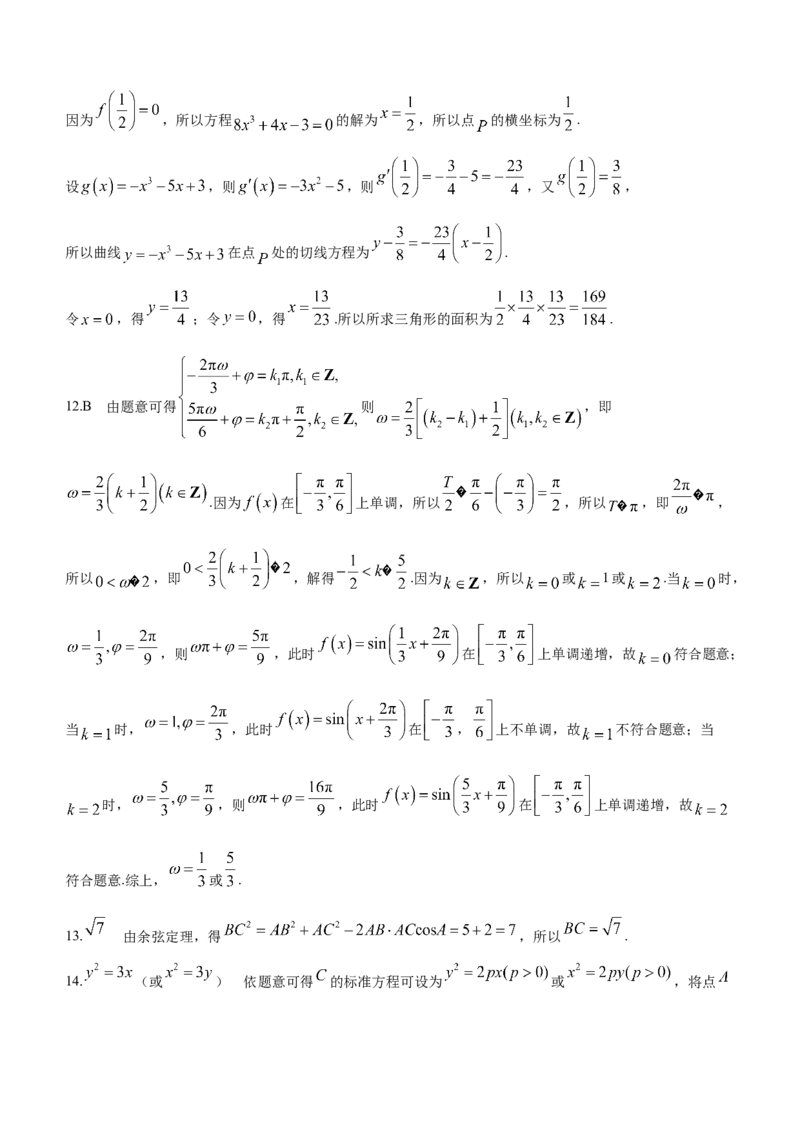文档内容
榆林市 2023—2024 年度高三第二次模拟检测
数学试题(理科)
考生注意:
1.本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.
2.请将各题答案填写在答题卡上.
3.本试卷主要考试内容:高考全部内容.
第I卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.若集合 ,则( )
A. B. C. D.
2.若向量 ,则 ( )
A.-4 B.-3 C. D.-2
3.若 ,则( )
A. B.
C. D.
4.某工厂要对1110个零件进行抽检,这1110个零件的编号为 .若采用系统抽样的方法抽
检30个零件,且编号为0005的零件被抽检,则下列编号是被抽检的编号的是( )
A.0040 B.0041 C.0042 D.0043
5.若 满足约束条件 则 的取值范围是( )
A. B. C. D.
6.甲、乙、丙、丁四人计划一起去陕西省榆林市旅游,他们从榆林古城、镇北台、红石峡、榆林沙漠国家森林公园、
红碱淖、白云山、易马城遗址这7个景点中选4个游玩(按照游玩的顺序,最先到达的称为第一站,后面到达
的依次称为第二、三、四站),已知他们第一站不去榆林沙漠国家森林公园,且第四站去红碱淖或白云山,则
他们这四站景点的选择共有( )
A.180种 B.200种 C.240种 D.300种
学科网(北京)股份有限公司7.若 ,则 ( )
A. B. C. D.
8.已知定义在 上的函数 满足 ,当 时, ,则
( )
A.1 B.2 C. D.-2
9.如图,网格纸中小正方形的边长为1,粗实线绘制的是一个几何体的三视图,则该几何体的表面积为
( )
A. B.
C. D.
10.已知 为双曲线 的两个焦点, 为 上一点,若 ,且 为等腰三角形,则
的离心率为( )
A. B.2 C. 或 D.2或3
11.已知曲线 与曲线 的公共点为 ,则曲线 在点 处的切线与
坐标轴围成的三角形的面积为( )
A. B. C. D.
12.已知函数 在 上单调, 的图象关于点 中心
学科网(北京)股份有限公司对称且关于直线 对称,则 的取值个数是( )
A.1 B.2 C.3 D.4
第II卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.
13.在 中, ,则 __________.
14.已知抛物线 经过点 ,写出 的一个标准方程:__________.
15.过球 外一点 作球 的切线,若切线长为5,且 ,则球 的体积为__________.
16.已知函数 恰有3个零点,则 的取值范围是__________.
三、解答题:共70分.解答应写出必要的文字说明、证明过程或演算步骤.17~21题为必考题,每
个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
蓝莓富含花青素,具有活化视网膜的功效,可以强化视力,防止眼球疲劳,是世界粮农组织推荐的五大健康
水果之一.截至2023年,全国蓝䔦种植面积达到110万亩,其中云南蓝莓种植面积达到17.6万亩,产量达到
10.5万吨,是蓝莓鲜果产量第一省.已知甲农户种植了矮丛蓝莓、高丛蓝莓、兔眼蓝莓3种蓝莓,这3种蓝莓年
产量各自达到1000斤的概率分别为 .
(1)求这3种蓝莓年产量都达到1000斤的概率;
(2)求这3种蓝莓中至多有1种蓝莓年产量达到1000斤的概率.
18.(12分)
已知数列 满足 .
(1)证明: 为等差数列.
(2)记 为数列 的前 项和,求 .
19.(12分)
如图,在底面是正方形的四棱柱 中, 平面 , .
学科网(北京)股份有限公司(1)证明:四棱柱 为正四棱柱.
(2)设二面角 为 ,求 .
20.(12分)
已知 为函数 的导函数.
(1)讨论 的单调性;
(2)若 ,证明:当 时, .
21.(12分)
已知椭圆 的左、右焦点分别为 过点 ,且 .
(1)求 的方程.
(2)设 的右顶点为点 ,过点 的直线 与 交于 两点(异于 ),直线 与 轴分
别交于点 ,试问线段 的中点是否为定点?若是,求出该定点的坐标;若不是,请说明理由.
(二)选考题:共10分.请考生从第22,23两题中任选一题作答.如果多做,则按所做的第一个
题目计分.
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系 中,曲线 的参数方程为 ( 为参数),曲线 的参数方程为 (
为参数 .
(1)求曲线 与曲线 的交点坐标;
学科网(北京)股份有限公司(2)求曲线 的普通方程.
23.[选修4-5:不等式选讲](10分)
已知函数 .
(1)当 时,求不等式 的解集;
(2)若 恒成立,求 的取值范围.
榆林市 2023—2024 年度高三第二次模拟检测
数学试题参考答案(理科)
1.C 依题意可得 .
2.A 若 ,则 ,即 ,解得 .
3.D 因为 ,所以 解得 所以 .
4.C 因为组距为 ,所以由 ,得被抽检的编号可以是0042.
5.A 作出约束条件表示的可行域,如图所示,当直线 经过点 时, 取得最大值12,所以
的取值范围是 .
学科网(北京)股份有限公司6.B 依题意可得他们这四站景点的选择共有 种.
7.A 因为 ,所以 ,
.
8.B 因为 ,所以 ,所以 是以4为周期的周期函数,
所以 .
9.D 由三视图可知,该几何体由一个棱长为2的正方体和一个底面半径为 ,高为2的圆柱拼接而成,故
该几何体的表面积为 .
10.C 因为 ,所以可设 ,依题意可得
或 ,故 的离心率 或
.
11.B 由 得 ,设 ,则 为增函数,
学科网(北京)股份有限公司因为 ,所以方程 的解为 ,所以点 的横坐标为 .
设 ,则 ,则 ,又 ,
所以曲线 在点 处的切线方程为 .
令 ,得 ;令 ,得 .所以所求三角形的面积为 .
12.B 由题意可得 则 ,即
.因为 在 上单调,所以 ,所以 ,即 ,
所以 ,即 ,解得 .因为 ,所以 或 1或 .当 时,
,则 ,此时 在 上单调递增,故 符合题意;
当 时, ,此时 在 , 上不单调,故 不符合题意;当
时, ,则 ,此时 在 上单调递增,故
符合题意.综上, 或 .
13. 由余弦定理,得 ,所以 .
14. (或 ) 依题意可得 的标准方程可设为 或 ,将点
学科网(北京)股份有限公司的坐标代入得 ,则 的标准方程为 或 .
15. 设切点为 ,则 ,所以 ,则球 的半径为 ,所以
球 的体积为 .
16. 令 ,
得 或 .作出 的大致图象,
如图所示,这两个函数图象的交点为 ,因为 , ,所以由图可知 的取值
范围是 .
17.解:(1)这3种蓝莓年产量都达到1000斤的概率为 .
(2)这3种蓝莓中没有1种蓝莓年产量达到1000斤的概率为 ,
这3种蓝莓中恰有1种蓝莓年产量达到1000斤的概率为
,
则这3种蓝莓中至多有1种蓝莓年产量达到1000斤的概率为 .
18.(1)证明:因为 ,所以 ,
所以 ,
学科网(北京)股份有限公司所以 为公差是8的等差数列.
(2)解:因为 ,所以 ,
所以 ,则 ,
所以 或 .
19.(1)证明:因为 ,
所以 ,则 .
又 平面 ,所以
因为 ,所以 平面 .
又底面 为正方形,所以四棱柱 为正四棱柱.
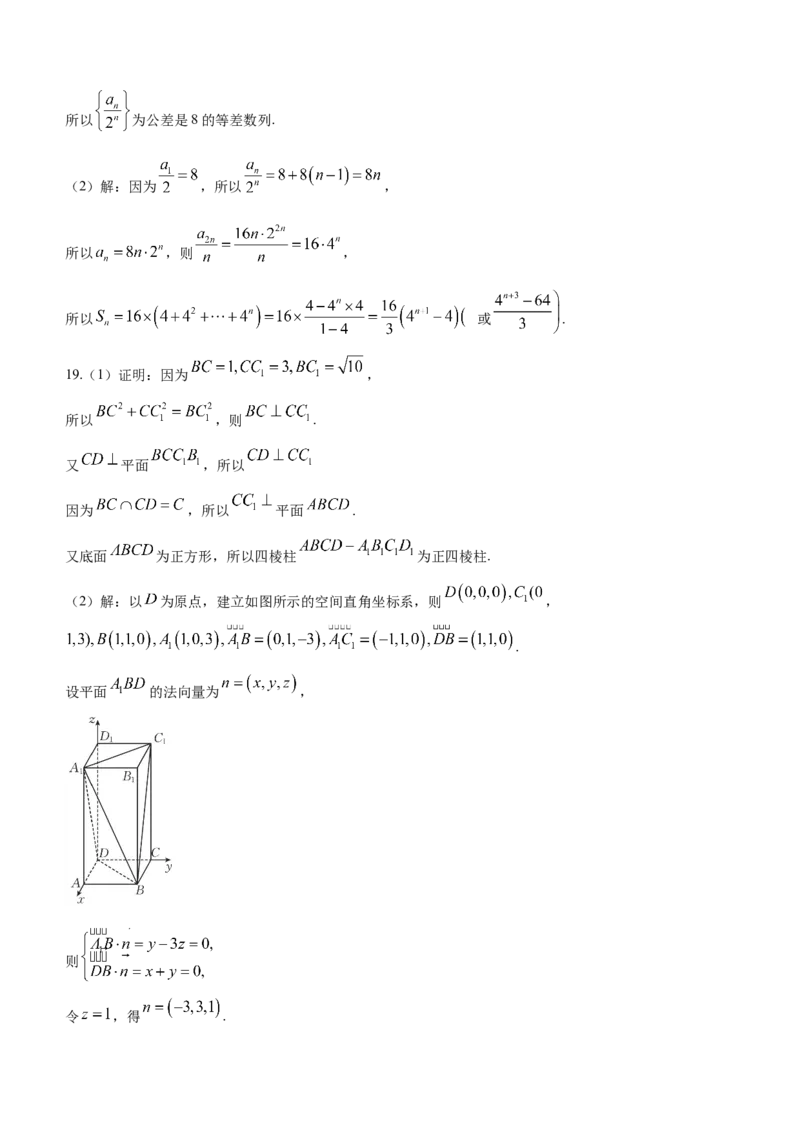
(2)解:以 为原点,建立如图所示的空间直角坐标系,则 ,
.
设平面 的法向量为 ,
则
令 ,得 .
学科网(北京)股份有限公司设平面 的法向量为 ,
则
令 ,得 .
由 ,
得 .
20.(1)解:因为 ,所以 .
令 ,则 .
当 ,即 时,则 在 上恒成立,
所以 单调递增.
当 ,即 时,令 ,解得 ,则当 时, ,
单调递减,当 时, 单调递增.
综上,当 时, 的单调递增区间为 ,无单调递减区间;当 时, 的单调递增区
间为 ,单调递减区间为 .
(2)证明:因为 ,所以 ,
则欲证 ,只需证 ,
只需证 ,即证 .
令 ,则 在
学科网(北京)股份有限公司上恒成立,则 在 上单调递增,故当 时, ,从而
,则结论成立.
21.解:(1)因为 ,
所以 ,则 ,
所以 ,则 ,
所以 ,
则 ,所以 的方程为 .
(2)易知 ,则直线 的斜率存在,设其方程为
联立 得 ,
.
因为点 在直线 上,所以 ,
,
直线 ,令 ,得 ,
直线 ,令 ,得 ,
学科网(北京)股份有限公司,
所以线段 的中点为 ,为定点.
22.解:(1)由曲线 的参数方程,得 ,
由 ,得 ,
则
故曲线 与曲线 的交点坐标为 .
(2)由 得 ,
则 ,代入 ,得 ,
整理得 ,
因为 ,
所以曲线 的普通方程为 .
23.解:(1)当 时, 可化为 .
当 时, 解得 ;
当 时, 解得 ;
当 时, 解得 .
学科网(北京)股份有限公司故当 时,不等式 的解集为 .
(2)因为 ,
所以 等价于 .
因为 ,
所以 的最小值为 ,所以 ,
解得 或 ,故 的取值范围是 .
学科网(北京)股份有限公司