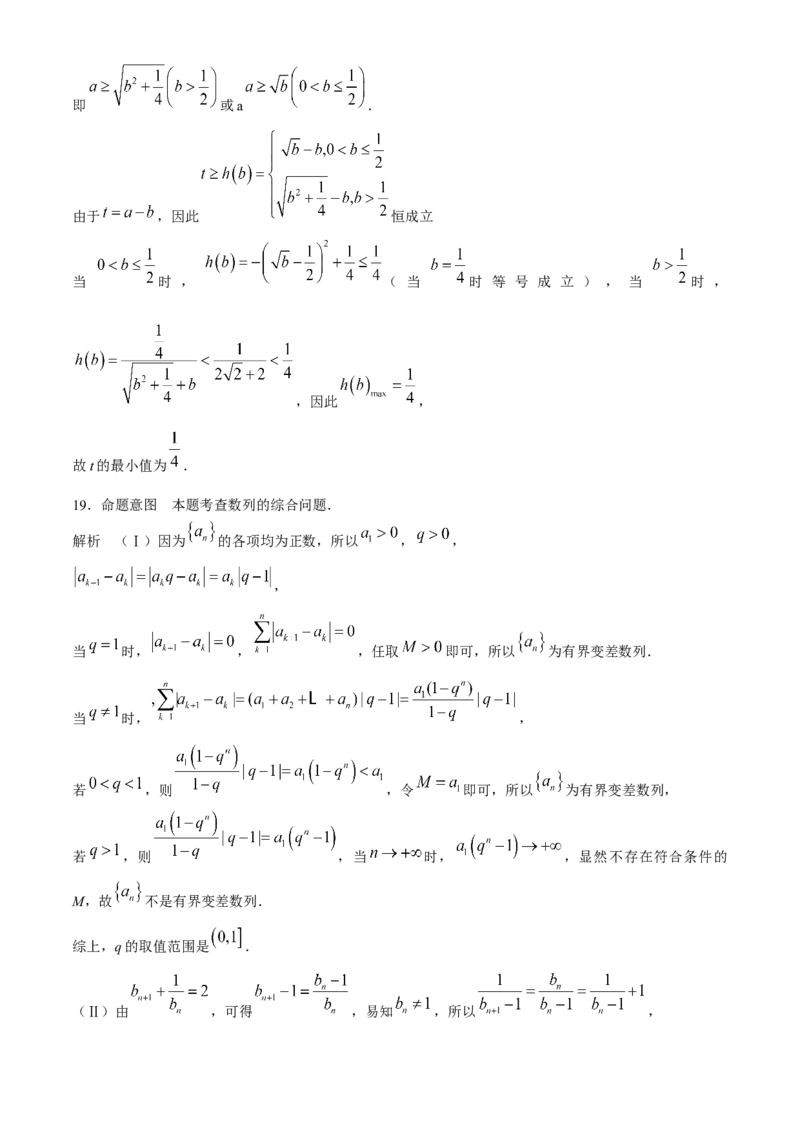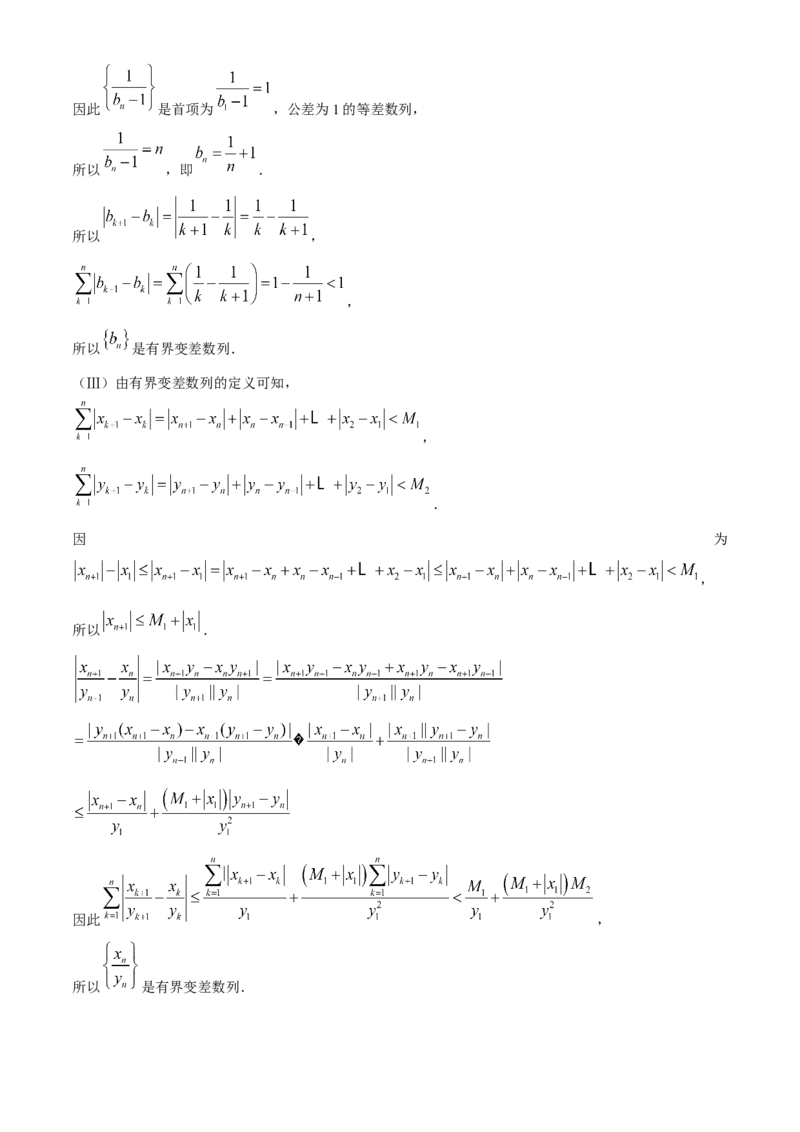文档内容
绝密★启用前 【山西专版】
天一大联考
2023—2024 学年高三年级阶段性测试(定位)
数学
考生注意:
1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴
在答题卡上的指定位置.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在
本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共 8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.设全集 ,集合 , ,则 =
A. B. C. D.
2. 的展开式中常数项为
A.112 B.56 C.28 D.16
3.已知函数 若对任意 ,,曲线 在点
和 处的切线互相平行或重合,则实数a=
A.0 B.1 C.2 D.3
4.干支纪年法源于中国,中国自古便有十天干与十二地支,十天干即:甲、乙、丙、丁、戊、己、庚、
辛、壬、癸;十二地支即:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.干支纪年法是按顺序以
一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第
一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,排列到“癸酉”后,天干回到“甲”重新
开始,即“甲戌”、“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,依此类推.已知2024年
是甲辰年,则2124年为
A.丁辰年 B.癸未年 C.甲午年 D.甲申年
5.将一个圆台的侧面展开,得到的扇环的内弧长为 4π,外弧长为8π,外弧半径与内弧半径之差为m,若
该圆台的体积为 ,则m=
学科网(北京)股份有限公司A.4 B.3 C.2 D.1
6.设非零复数 和 在复平面内对应的向量分别为 和 ,其中O为原点,若 为纯虚数,
则
A. B.
C. D.
7 . 已 知 α , β , γ 均 是 锐 角 , 设 的 最 大 值 为 , 则
=
A. B. C.1 D.
8.已知实数a,b,c满足 , , ,则
A. B. C. D.
二、多项选择题:本题共 3小题,每小题6分,共18分.在每小题给出的选项中,有多项符
合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知抛物线C: 的焦点为F,点 在C上,若∠MOF=45°(O为坐标原点),则
A. B. C. D.
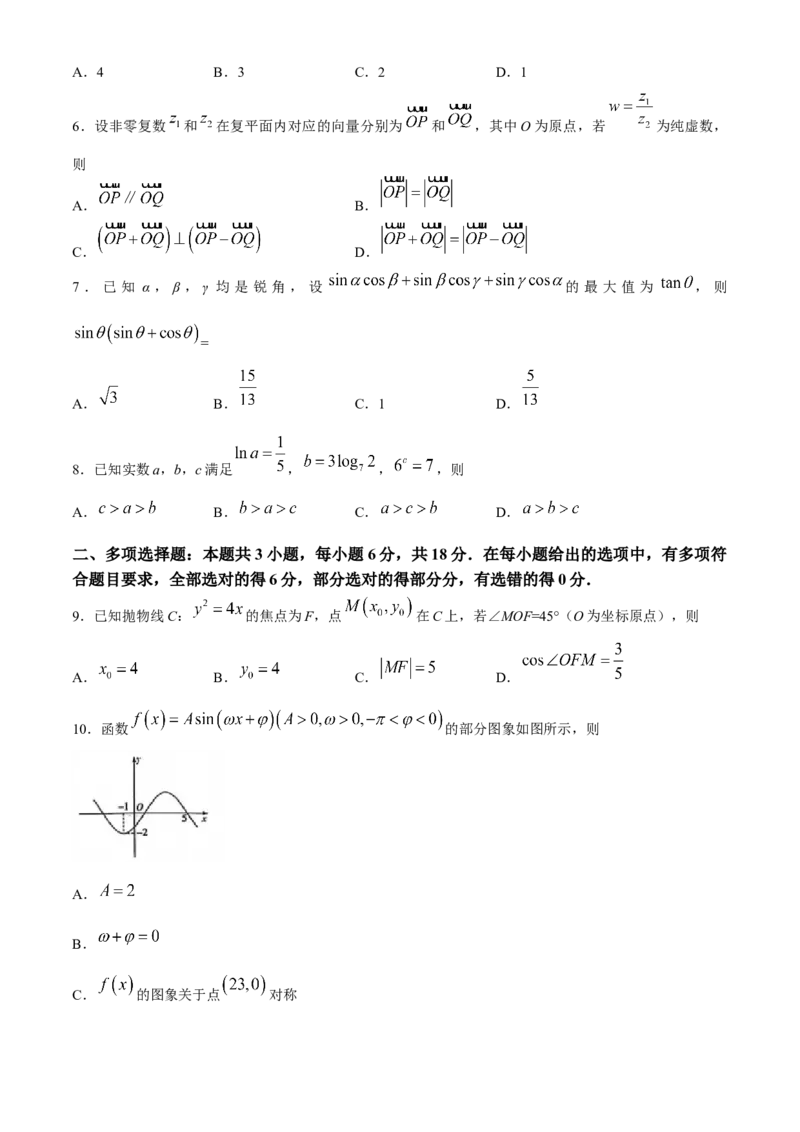
10.函数 的部分图象如图所示,则
A.
B.
C. 的图象关于点 对称
学科网(北京)股份有限公司D.不等式 的解集为
11 . 在 四 棱 锥 中 , 已 知 , , 且
,则
A.四棱锥 的体积的取值范围是
B. 的取值范围是
C.四棱锥 的外接球的表面积的最小值为8π
D.PB与平面PAD所成角的正弦值可能为
三、填空题:本题共3小题,每小题5分,共15分.
12.已知圆C经过点 ,且有一条直径的两个端点分别在 x,y轴上,则圆C的面积的最小值为
______.
13.甲、乙两名足球运动员进行射门比赛,约定每人射门3次,射进的次数多者赢,一样多则为平局.若
甲每次射门射进的概率均为 ,乙每次射门射进的概率均为 ,且每人每次射门相互独立.现已知甲第一
次射门未射进,则乙赢的概率为______.
14.已知椭圆C: 的左、右焦点分别是 , ,斜率为 的直线l经过点 且
交C于A,B两点(点A在第一象限),若 的面积是 的面积的3倍,则C的离心率为
______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
某学校准备订做新的校服,有正装和运动装两种风格可供选择,为了解学生和家长们的偏好,学校随机调
查了200名学生及每名学生的一位家长,得到以下的2×2列联表:
更喜欢正装 更喜欢运动装
家长 120 80
学生 160 40
(Ⅰ)根据以上数据,判断是否有99%的把握认为学生与家长对校服风格的偏好有差异;
(Ⅱ)若从家长中按不同偏好的人数比例用分层随机抽样的方法抽取5人进行座谈,再从这5人中任选2
学科网(北京)股份有限公司人,记这2人中更喜欢正装的家长人数为X,求X的分布列和数学期望.
附: .
0.1 0.05 0.01 0.001
2.706 3.841 6.635 10.828
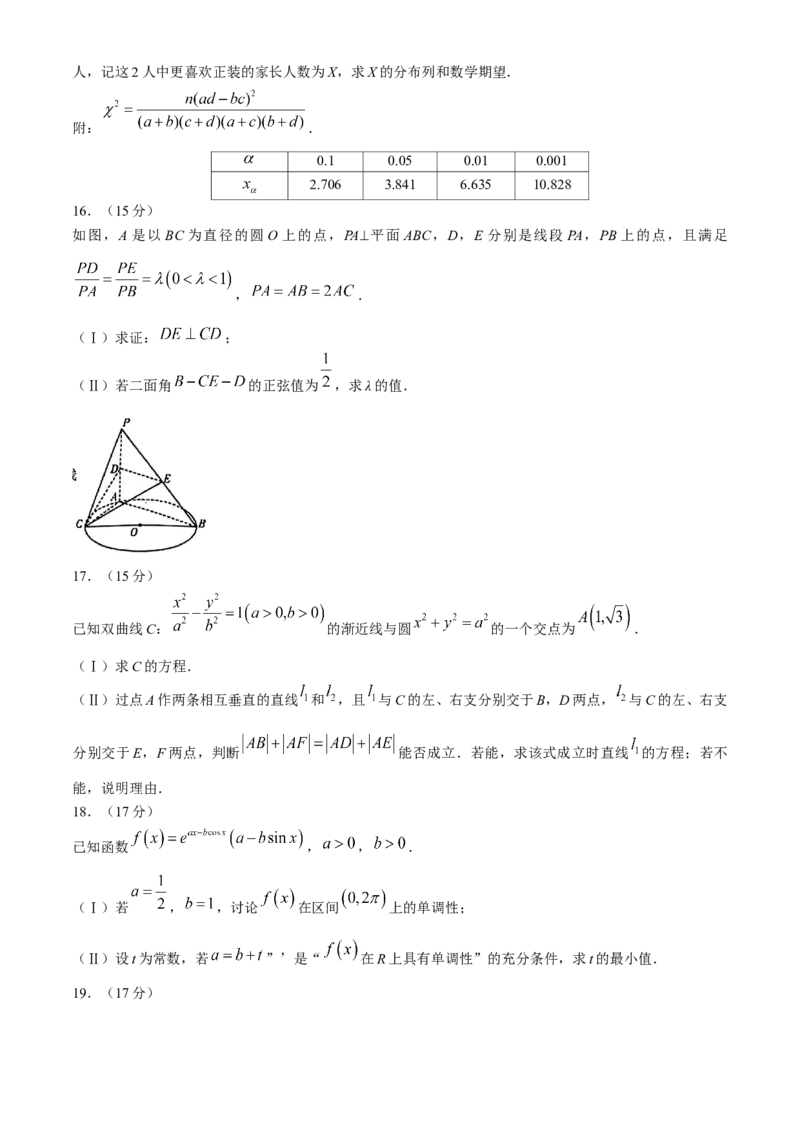
16.(15分)
如图,A 是以 BC 为直径的圆 O 上的点,PA⊥平面 ABC,D,E 分别是线段 PA,PB 上的点,且满足
, .
(Ⅰ)求证: ;
(Ⅱ)若二面角 的正弦值为 ,求λ的值.
17.(15分)
已知双曲线C: 的渐近线与圆 的一个交点为 .
(Ⅰ)求C的方程.
(Ⅱ)过点A作两条相互垂直的直线 和 ,且 与C的左、右支分别交于B,D两点, 与C的左、右支
分别交于E,F两点,判断 能否成立.若能,求该式成立时直线 的方程;若不
能,说明理由.
18.(17分)
已知函数 , , .
(Ⅰ)若 , ,讨论 在区间 上的单调性;
(Ⅱ)设t为常数,若 ”’是“ 在R上具有单调性”的充分条件,求t的最小值.
19.(17分)
学科网(北京)股份有限公司对于数列 ,若存在 ,使得对任意 ,总有 ,则称 为“有界变差数
列”.
(Ⅰ)若各项均为正数的等比数列 为有界变差数列,求其公比q的取值范围;
(Ⅱ)若数列 满足 ,且 ,证明: 是有界变差数列;
(Ⅲ)若 , 均为有界变差数列,且 ,证明: 是有界变差数列.
天一大联考
2023—2024 学年高三年级阶段性测试(定位)
数学(山西专版)答案
一、单项选择题:本题共8小题,每小题5分,共40分.
1.答案 C
命题意图 本题考查集合的表示与运算.
解析 由已知易得 ,所以 .
2.答案 A
命题意图 本题考查二项式定理的应用.
解析 常数项为 .
3.答案 C
命题意图 本题考查导数的几何意义和函数的奇偶性.
解析 由题意知 为偶函数,则 .
4.答案 D
命题意图 本题考查等差数列的应用.
解析 天干可看作公差为10的等差数列,地支可看作公差为12的等差数列,由于 ,
故100年后天干为甲,由于 ,余数为 4,故100年后地支为“辰”后面第四个,即
“申”,所以2124年为甲申年.
5.答案 B
命题意图 本题考查圆台的有关计算.
学科网(北京)股份有限公司解析 易知圆台的上底面半径为2,下底面半径为4,母线长为m.设圆台的高为h,根据题意可知该圆台
的 体 积 为 , 解 得 , 则
.
6.答案 D
命题意图 本题考查复数的几何意义以及平面向量的运算.
解析 设 , , ,其中a,b,c,d, ,且a,b不同时为0,c,d不同时
为 0 , , 由 题 意 , 所 以
,所以 .
7.答案 B
命题意图 本题考查三角恒等变换及基本不等式的应用.
解 析 由 基 本 不 等 式 可 得 , ,
,三式相加,可得 ,当且仅当α,
β , γ 均 为 时 等 号 成 立 , 所 以 , 则
.
8.答案 C
命题意图 本题考查指数函数和对数函数的综合性质.
解 析 由 已 知 得 , , . 令 , 则
, 显 然 , 即 单 调 递 减 , 所 以 , 即
,亦即 , .由 ,可得 ,而
学科网(北京)股份有限公司,所以 ,所以 .综上可知 .
二、多项选择题:本题共3小题,每小题6分,共18分.每小题全部选对的得6分,部分选
对的得部分分,有选错的得0分.
9.答案 AC
命题意图 本题考查抛物线的方程与性质.
解析 若∠MOF=45°,则 ,又 ,解得 或 ,故A正确,B
错 误 ; 由 抛 物 线 的 定 义 , 得 , 故 C 正 确 ; 由 余 弦 定 理 得
,故D错误.
10.答案 ABD
命题意图 本题考查三角函数的图象与性质.
解析 设 的最小正周期为 T,由图象可知 , 解得 ,故
,则 ,将 代入解析式,得 ,所以
,所以 ,故A,B正确; ,故C
错 误 ; 即 为 , 得 , 得
,得 ,故D正确.
11.答案 BCD
命题意图 本题考查棱锥的结构以及棱锥与球的综合问题.
解析 由已知可得,四边形 ABCD 是上底为 1,下底为 2,底角为 60°的等腰梯形,所以
, .
学科网(北京)股份有限公司对于A,当PD⊥底面ABCD时,四棱锥 的体积最大,最大体积为 ,故A错
误;对于B,在 中, , , ,用余弦定理可知 的取值
范围是 ,故B正确;
对于C,当PD⊥平面ABCD时,四棱锥 的外接球的半径等于 的外接圆的半径,此时外
接球的半径最小,为 ,故外接球的表面积的最小值为 ,故C正确;
对于D,设PB与平面PAD所成角为θ,当PD⊥平面ABCD时,计算可得 ,当
P靠近平面ABCD时,θ趋向于0,所以存在某个P点,使得 ,故D正确.
三、填空题:本题共3小题,每小题5分,共15分.
12.答案 25π
命题意图 本题考查圆的方程与性质.
解析 因为圆 C 的一条直径的两个端点分别在 x,y 轴上,所以该圆一定过原点 O.又圆 C 经过点
,所以当OM为圆C的直径时,圆C的面积最小,又 .所以圆C的面积
最小值为 .
13.答案
命题意图 本题考查概率的乘法公式.
解析 若乙射进1次,则他赢的概率为 ;若乙射进2次,则他赢的概率
为 ;若乙射进3次,则他赢的概率为 .故乙赢的概率
为 .
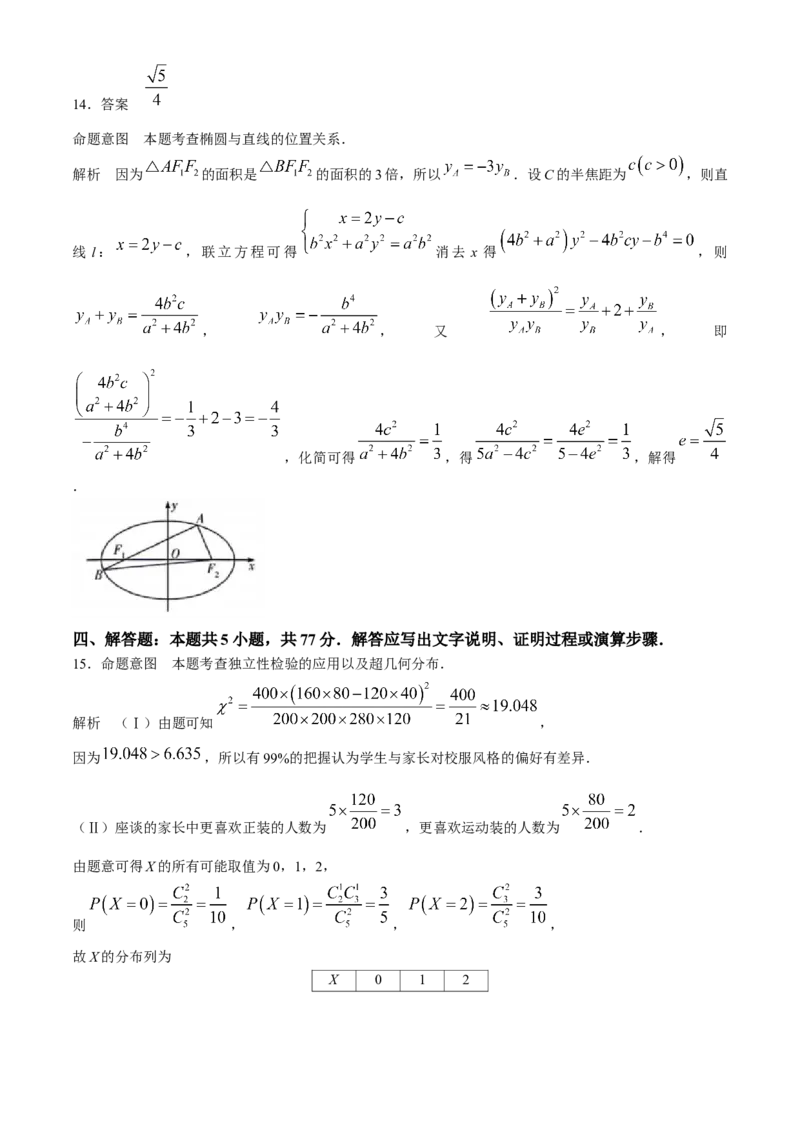
学科网(北京)股份有限公司14.答案
命题意图 本题考查椭圆与直线的位置关系.
解析 因为 的面积是 的面积的3倍,所以 .设C的半焦距为 ,则直
线 l: ,联立方程可得 消去 x 得 ,则
, , 又 , 即
,化简可得 ,得 ,解得
.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.命题意图 本题考查独立性检验的应用以及超几何分布.
解析 (Ⅰ)由题可知 ,
因为 ,所以有99%的把握认为学生与家长对校服风格的偏好有差异.
(Ⅱ)座谈的家长中更喜欢正装的人数为 ,更喜欢运动装的人数为 .
由题意可得X的所有可能取值为0,1,2,
则 , , ,
故X的分布列为
X 0 1 2
学科网(北京)股份有限公司P
所以X的数学期望 .
16.命题意图 本题考查空间位置关系的推理与证明、二面角的计算.
解析 (Ⅰ)因为A是以BC为直径的圆O上异于B,C的点,所以 ,
因为PA⊥平面ABC,所以 .
又 ,所以AB⊥平面PAC,
因为 ,所以 ,所以DE⊥平面PAC,
因为 平面PAC,所以 .
(Ⅱ)分别以AC,AB,AP所在的直线为x,y,z轴建立如图所示的空间直角坐标系.
设 , , 则 点 , , , ,
, 则 , , ,
设平面CDE的法向量为 ,
则 取 .
设平面BCE的法向量为 ,
则 取 .
学科网(北京)股份有限公司因为二面角 的正弦值为 ,
所以 ,
解得 或 (舍去).
17.命题意图 本题考查双曲线的性质,双曲线与直线的位置关系.
解析 (Ⅰ)由题可知 ,
, ,
故C的方程为 .
(Ⅱ)不能成立.
显 然 直 线 , 的 斜 率 均 存 在 , 设 直 线 的 方 程 为 , 直 线 的 方 程 为
, , .(6分)
联立 与C的方程可得 得 ,
因为 与C的左、右支分别相交,所以 ,
同理 ,解得 或 .(*)
因为 ,
所以 ,
学科网(北京)股份有限公司同理可得 .
若 ,则 ,
只需 即可,解得 , ,
显然 , 都不符合(*).
所以 不能成立.
18.命题意图本题考查利用导数研究函数的单调性.
解析由题可知 ,
即 .
(I) , ,则 .
由 得 , 即 或 ; 由 得 , 即
.
因此 在 上单调递减,在 上单调递增,在 上单调递减.
(Ⅱ)若 具有单调性,则 不变号.
设 ,则 ,即 不变号,由于 ,因此 是二次函数.
若 在 恒成立,则 即 由于 , ,所以该情形不成立.
若 在 恒成立,则 或
学科网(北京)股份有限公司即 或a .
由于 ,因此 恒成立
当 时 , ( 当 时 等 号 成 立 ) , 当 时 ,
,因此 ,
故t的最小值为 .
19.命题意图 本题考查数列的综合问题.
解析 (Ⅰ)因为 的各项均为正数,所以 , ,
,
当 时, , ,任取 即可,所以 为有界变差数列.
当 时, ,
若 ,则 ,令 即可,所以 为有界变差数列,
若 ,则 ,当 时, ,显然不存在符合条件的
M,故 不是有界变差数列.
综上,q的取值范围是 .
(Ⅱ)由 ,可得 ,易知 ,所以 ,
学科网(北京)股份有限公司因此 是首项为 ,公差为1的等差数列,
所以 ,即 .
所以 ,
,
所以 是有界变差数列.
(Ⅲ)由有界变差数列的定义可知,
,
.
因 为
,
所以 .
因此 ,
所以 是有界变差数列.
学科网(北京)股份有限公司