文档内容
长沙市第一中学 2023—2024 学年度高二第二学期第二次阶段性检测
数学
时量:120分钟 满分:150分
得分__________.
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的)
1.已知复数 满足 ,则复数 的虚部为( )
A. B. C. D.
2.已知某校高三(1)班有51名学生,春季运动会上,有17名学生参加了田赛项目,有22名学生参加了
径赛项目,田赛和径赛都参加的有9名同学,则该班学生中田赛和径赛都没有参加的人数为( )
A.25 B.23 C.21 D.19
3.已知向量 ,则向量 在向量 上的投影向量的坐标为( )
A. B. C. D.
4.已知直线 是三条不同的直线,平面 是三个不同的平面,下列命题正确的是( )
A.若 ,则
B.若 ,则
C.若 ,且 ,则
D.若 ,且 ,则
5.若将大小形状完全相同的三个红球和三个白球(除颜色外不考虑球的其他区别)排成一排,则有且只有
两个白球相邻的排法有( )
A.6 B.12 C.18 D.36
6.若 ,设 ,则 的大小关系为( )
A. B.
C. D.7.已知等比数列 的前 项和为 ,若 恒成立,则 的最小值为( )
A. B. C. D.1
8.已知 ,且 ,则 的最大值为( )
A.9 B.12 C.36 D.48
二、多选题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.关于二项式 的展开式,下列说法正确的有( )
A.有3项
B.常数项为3
C.所有项的二项式系数和为8
D.所有项的系数和为0
10.已知曲线 ,则( )
A.曲线 在第一象限为双曲线的一部分
B.曲线 的图象关于原点对称
C.直线 与曲线 没有交点
D.存在过原点的直线与曲线 有三个交点
11.若定义域为 的函数 不恒为零,且满足等式 ,则下列说法正确的是
( )
A. B. 在定义域上单调递增
C. 是偶函数 D.函数 有两个极值点
三、填空题(本题共3小题,每小题5分,共15分)
12.某小球可以看作一个质点,沿坚直方向运动时其相对于地面的高度 (单位: )与时间 (单位:
s)存在函数关系 ,则该小球在 时的瞬时速度为__________ .
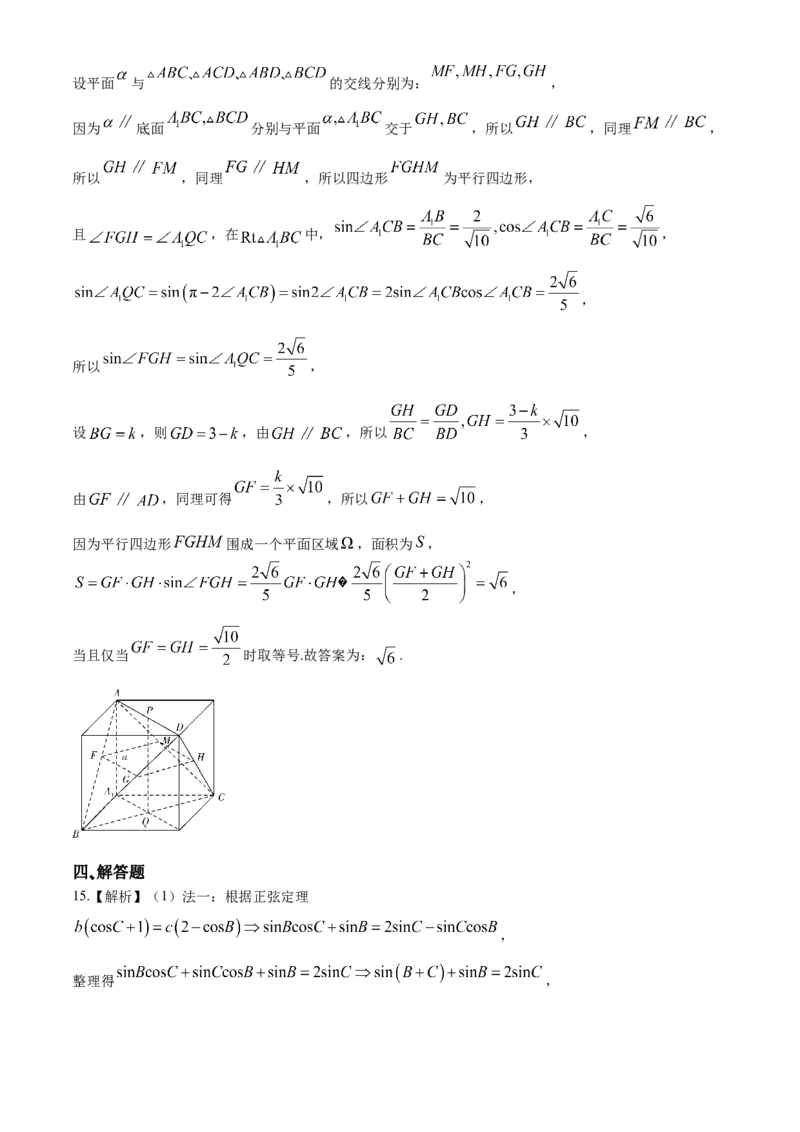
13.若随机变量 服从正态分布 ,且 ,则 __________.14.在四面体 中,且 ,点 分别是线段 ,
的中点,若直线 平面 ,且 截四面体 形成的截面为平面区域 ,则 的面积的最大
值为__________.
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分13分)
在 中,内角 的对边分别为 ,且 .
(1)证明: ;
(2)若 ,求 的面积.
16.(本小题满分15分)
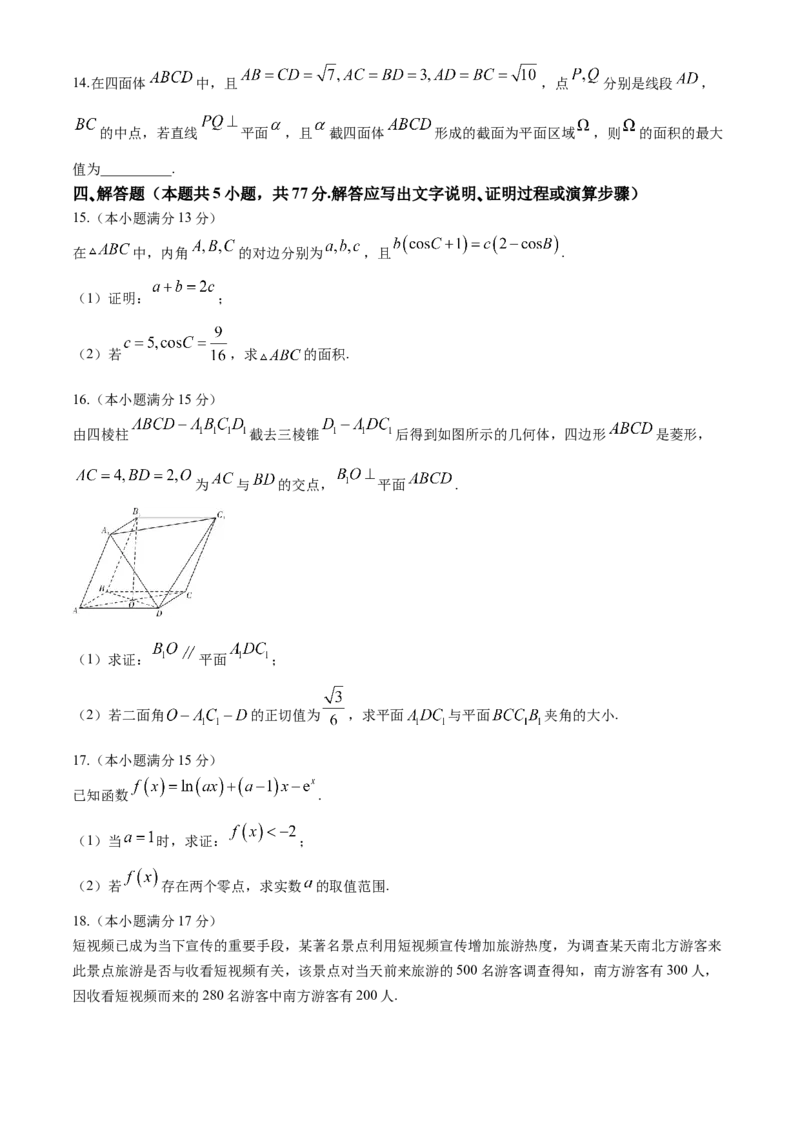
由四棱柱 截去三棱锥 后得到如图所示的几何体,四边形 是菱形,
为 与 的交点, 平面 .
(1)求证: 平面 ;
(2)若二面角 的正切值为 ,求平面 与平面 夹角的大小.
17.(本小题满分15分)
已知函数 .
(1)当 时,求证: ;
(2)若 存在两个零点,求实数 的取值范围.
18.(本小题满分17分)
短视频已成为当下宣传的重要手段,某著名景点利用短视频宣传增加旅游热度,为调查某天南北方游客来
此景点旅游是否与收看短视频有关,该景点对当天前来旅游的500名游客调查得知,南方游客有300人,
因收看短视频而来的280名游客中南方游客有200人.短视频
游客 合计
收看 未看
南方游客
北方游客
合计
(1)依据调查数据完成如下列联表,并根据小概率值 的独立性检验,分析南北方游客来此景点
旅游是否与收看短视频有关联;
(2)为了增加游客的旅游乐趣,该景点设置一款5人传球游戏,每个人得到球后都等可能地传给其余4人
之一,现有甲、乙等5人参加此游戏,球首先由甲传出.
(i)若 ,求经过 次传递后球回到甲的概率;
(ii)已知 ,记前 次传递中球传到乙的次数为 ,求 的数学期望.
参考公式: ,其中 ;若 为随机变量,则
.
附表:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
19.(本小题满分17分)
已知双曲线 ,过 的直线 与双曲线 的右支交于 两点.
(1)若 ,求直线 的方程,
(2)设过点 且垂直于直线 的直线 与双曲线 交于 两点,其中 在双曲线的右支上.
(i)设 和 的面积分别为 ,求 的取值范围;
(ii)若 关于原点对称的点为 ,证明: 为 的垂心,且 四点共圆.长沙市第一中学 2023—2024 学年度高二第二学期第二次阶段性检测
数学参考答案
一、二、选择题
题号 1 2 3 4 5 6 7 8 9 10 11
答案 A C B D B D C C BCD AC AD
1.A 【解析】 ,故 的虚部为 .故选:A.
2.C 【解析】设高三(1)班有51名学生组成的集合为 ,参加田赛项目的学生组成的集合为 ,参加
径赛项目的学生组成的集合为 ,由题意集合 有17个元素, 有22个元素, 中有9个元素,所
以 有 个元素.所以该班学生中田赛和径赛都没有参加的人数为 .故选:
C.
3.B 【解析】 ,
向量 在向量 上的投影向量为 ,故选:B.
4.D 【解析】对于A,若 ,则 可能平行,可能异面,可能相交,故A错误;
对于B,若 ,则 或 ,故B错误;
对于C,以长方体 为例, 平面 平面,但 与平面 不垂直,故C错误;故选D.
5.B 【解析】除颜色外不考虑球的其他区别,将三个白球分成两堆,只有一种分法,大小形状完全相同的
三个红球排成一排也只有一种排法,将白球插空有 种可能,故选:B.
6.D 【解析】由题意知 ,由 ,
所以 为偶函数,当 单调递增,
因为 ,且 ,所以
,
所以 ,即 .故选:D.
7.C 【解析】设等比数列 的公比为 ,由 ,得 ,
则 ,即 ,
因为 ,所以 ,解得 ,所以 ,
所以 ,
当 为奇数时, ,所以 ,
当 为偶数时, ,所以 ,所以 .故选:C.
8.C 【解析】依题意, 与 为圆 上一点,且 ,得 为
等腰直角三角形,设 为 的中点,则点 在以 为圆心,2为半径的圆上,即 ,故 ,
因为点 到定点 的距离的最大值为 ,因此 的最大值为36.
9.BCD 【解析】对A,因为二项式 的展开式中共有4项,故A错误;
对B,二项式 的展开式中通项为 ,令
,得 ,所以常数项为 ,故B正确;
对C,二项式 中,所有项的二项式系数和为 ,故C正确;
对D,令 ,得 ,故D正确.故选:BCD.
10.AC 【解析】当 时,曲线 ,为焦点在 轴上的双曲线的一部分;
当 时,曲线 ,为焦点在 轴的棈圆的一部分;
当 时,曲线 ,为焦点在 轴上的双曲线的一部分;
当 时,曲线 没有图象.
由图象可知,A正确,B错误,结合曲线 的渐近线可知C正确,D错误.
11.AD 【解析】对于 ,令 得 ,即 ,A正确;对于B,若 在定义域上单调递增,当 时, ,令 ,得
,即 ,与 在定义域上单调递增矛盾,故B错误;
对于C,若 是偶函数,则 ,且 ,因为 ,
所以 ,所以 ,即 ,
得 或 ,又 ,所以 恒成立,矛盾,故C错误;
对于D,当 时, ,记 ,
则 ,
所以 ,令 ,
解得 ,因为 不恒为零,所以在 两边 异号,
所以 为 的极值点,所以函数 有两个极值点,D正确.故选:AD
三、填空题
12.-2 【解析】由函数 ,可得 ,则 ,
所以该小球在 时的瞬时速度为-2.故答案为:-2.
13.0.34 【解析】 服从正态分布 ,则 .
故答案为0.34.
14. 【解析】四面体 拓展为长方体,如图所示, ,
设 ,则有
因为点 分别是线段 的中点,所以 底面 ,
又有直线 平面 ,所以 底面 ,设平面 与 的交线分别为: ,
因为 底面 分别与平面 交于 ,所以 ,同理 ,
所以 ,同理 ,所以四边形 为平行四边形,
且 ,在 中, ,
,
所以 ,
设 ,则 ,由 ,所以 ,
由 ,同理可得 ,所以 ,
因为平行四边形 围成一个平面区域 ,面积为 ,
,
当且仅当 时取等号.故答案为: .
四、解答题
15.【解析】(1)法一:根据正弦定理
,
整理得 ,因为 ,所以 ,
由正弦定理可得 ;
法二:由 ,
由射影定理知 (因为 ),故 .
(2)因为 ,由余弦定理可得 ,即 ,
又 ,故 ,从而 ,解得 ,
因为 ,所以 ,
所以 .
16.【解析】(1) 四边形 是菱形, 为 与 的交点, 平面 .
以直线 分别为 轴, 轴, 轴,建立空间直角坐标系,
则 ,设 ,
由 得 ,
由 得 ,则 ,设平面
的法向量为 ,
则 取 ,得 ,
,又 平面 ,
平面 .
(2)取 的中点 ,则 ,又四边形 是菱形, 平面
,故 面 ,则 ,又 ,故 .所以 为二面角 的平面角.
则 ,得 ,
故 ,
设平面 的法向量为 ,
则 取 ,得 ,
,
平面 与平面 夹角的余弦值为 ,
平面 与平面 夹角为 .
法二:(1)将几何体补成四棱柱,用常规法做.
(2)找到平面角两分,两个法向量各两分,后面一样.
17.【解析】(1)当 时, .
先证明: ,
设 ,则 ,即 ,即 ,
类似地有 ,
因此 ,证毕.
(2)令 ,得 ,
设 ,显然 在定义域上单调递增,而 ,
则 ,依题意,方程 有两个不等的实根,
显然 ,故 存在两个不同的零点,设 ,则 ,
(i)当 时,则 ,此时 在 上单调递增, 最多一个零点,不合题意;
(ii)当 时,此时 ,当 时, ,当 时, ,
在 上单调递增,在 上单调递减, ,
要使 有两个零点,则 ,解得 ,
综上可知, .
18.【解析】(1)将所给数据进行整理,得到如下列联表:
短视频
游客 合计
收看 未看
南方游客 200 100 300
北方游客 80 120 200
合计 280 220 500
零假设 :南北方游客来此景点旅游与短视频无关联.
,
根据小概率值 的独立性检验,我们推断 不成立,
即认为南北方游客来此景点旅游与收看短视频有关联,此推断犯错误的概率不大于0.001.
(2)(i)设经过 次传递后回到甲的概率为 ,
,又 ,所以 是首项为 ,公比为 的等比数列,
所以 .
(ii)方法一:设第 次传递时甲接到球的次数为 ,则 服从两点分布, ,设前 次传递中球传到甲的次数为 ,
,
因为 ,所以 .
方法二:设第 次传递时,乙接到球的概率和次数分别为 与 ,则 服从两点分布, ,
由题可知 ,
又 ,所以 ,所以 是首项为 ,公比为 的等比数列,
,
,
故 .
19.【解析】(1)设 ,直线 ,因为直线 与双曲线右支相交,故
,
联立双曲线方程 ,得 ,
则 ,
故 ,
即 ,解得 ,或 (舍去),因此 ,从而直线 的方程为 .
(2)(i)若 ,则 ,
由(1)可知, ,
此时 ;
当 时,设 ,直线 ,
由(1)同理可知 ,
故
注意到
,
令 ,则 ,
综上可知, 的取值范围是 .(ii)先证明 为 的垂心,只需证明 ,
注意到, ,
而
,
同理 ,
,
因此 ,又 ,故 为 的垂心,因此 ,
再证明 四点共圆,即只需证明: .
因为 关于原点对称,则 ,
同理可得 ;
则 ,即 ,
因此 ,因此 四点共圆.