数学答案_6月_240630浙江省台州市2023-2024学年高二下学期6月期末试题

参考答案
一、单项选择题：本题共 8小题，每小题 5分，共 40分。在每小题给出的四个
选项中，只有一项是符合题目要求的。
题号 1 2 3 4 5 6 7 8
答案 B D B A C C D B
二、多项选择题：本题共 3小题，每小题 6分，共 18分。在每小题给出的四个
选项中，有多项是符合题目要求的。全部选对得 6 分，部分选对得部分分，有
选错的得 0分。
题号 9 10 11
答案 BD ACD ACD
三、填空题：本题共 3小题，每小题 5分，共 15分。
1 2
12．40 13．2 2 ， （第一问3分，第二问2分） 14．
6 2
四、解答题：本小题共 5小题，共
77
分。解答应写出文字说明、证明过程或验
算步骤。
15．（本小题满分13分）
2π
解：（I）若选择①：由题知T   π，故2．

5 5π π
当x π时，2 2kπ ，kZ，
12 12 2
π π
故 2kπ，又0 π，故 ．
3 3
 π
所以 f  x 2sin2x ．
 3
2π
若选择②：由单调区间可知周期为π，故T   π，故2．

π  π  π
由题意知当x 时， f  x 取最小值，即2    2kπ ，kZ，
12  12 2
π π π
故 2kπ，又0 ，故 ．
3 2 3
 π
所以 f  x 2sin2x ．
 3
若选择③：令 f  x 1，即2sin x1，
π  5π  2π
由图象可知， x x     2kπ    2kπ  ，
1 2 6   6  32π π
即 x x   ，又 x x 的最小值为 ，故2．
2 1 min 3 1 2 3
π   π  π 
由 f  x  f  x  0，可知 ,0是 f  x 的对称中心，
6  6  6 
π π
则2  kπ，kZ，故 kπ，
6 3
π
又0 π，故 ．
3
 π
所以 f  x 2sin2x ．
 3
 x π 2 1
（Ⅱ）由 f  0    2sinx  ，得sinx  ．
 2 6 0 3 0 3
故 f  x  5π   2sin  2x  π   2cos2x  2  12sin2x   14 ．
 0 12  0 2 0 0 9
16．（本小题满分15分）
解：（Ⅰ） f  x 的定义域为  x x a  ，
由 f  x 是偶函数，知其定义域关于原点对称，故a 0；
1
当a0时， f  x  x  为偶函数。所以a0．
x
1
（Ⅱ） f  x bx恒成立即 x  bx（*）恒成立．
x
1
当x0时，（*）式恒成立等价于x bx恒成立，
x
1
即b1 恒成立，故b1；
x2
1
当x0时，（*）式恒成立等价于x bx 恒成立，
x
1
即b1 恒成立，故b1．
x2
综上可得，b的取值范围是1,1 ．
17．（本小题满分15分）
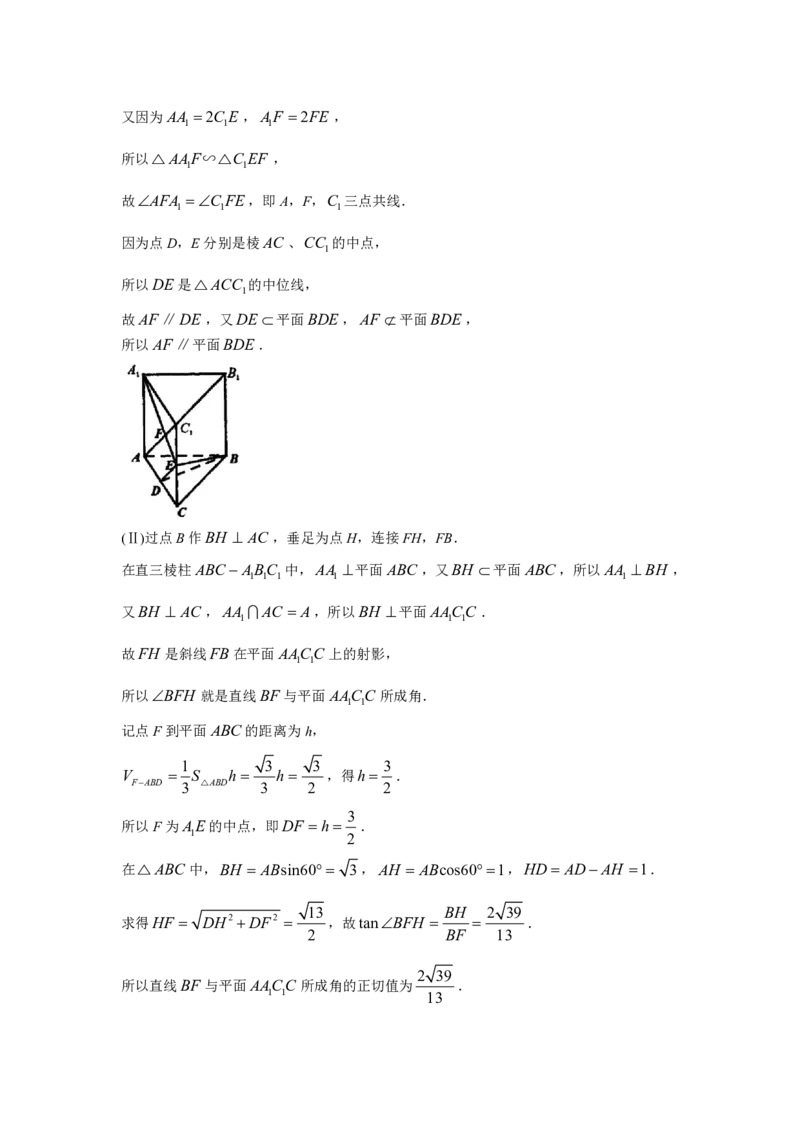
解：（I）连接C F ．
1
在直三棱柱ABCABC 中，AA ∥CC ，所以AAF C EF ．
1 1 1 1 1 1 1又因为AA 2C E ，AF 2FE ，
1 1 1
所以△AAF∽△C EF ，
1 1
故AFA C FE，即A，F，C 三点共线．
1 1 1
因为点D，E分别是棱AC 、CC 的中点，
1
所以DE是△ACC 的中位线，
1
故AF∥DE ，又DE 平面BDE，AF 平面BDE，
所以AF∥平面BDE．
(Ⅱ)过点B作BH  AC ，垂足为点H，连接FH，FB．
在直三棱柱ABCABC 中，AA 平面ABC，又BH 平面ABC，所以AA BH ，
1 1 1 1 1
又BH  AC，AA AC  A，所以BH 平面AACC ．
1 1 1
故FH 是斜线FB在平面AACC 上的射影，
1 1
所以BFH 就是直线BF 与平面AACC 所成角．
1 1
记点F到平面ABC的距离为h，
1 3 3 3
V  S h  h  ，得h ．
FABD
3
△ABD
3 2 2
3
所以F为AE的中点，即DF h ．
1 2
在△ABC中，BH  ABsin60 3，AH  ABcos601，HD  ADAH 1．
13 BH 2 39
求得HF  DH2DF2  ，故tanBFH   ．
2 BF 13
2 39
所以直线BF 与平面AACC 所成角的正切值为 ．
1 1 1318．（本小题满分17分）
x
解：（I）当a0时， f  x  ，函数 f  x 的定义域为 0,1    1,，
lnx
lnx1
f x  ，
ln2x
令 f x 0，解得xe；令 f x 0，解得0 x1或1 xe，
故函数 f  x 的单调递增区间是 e,，函数 f  x 的单调递减区间是 0,1 ， 1,e ．
x
（Ⅱ）当a 1时， f  x  ，函数 f  x 的定义域为1,0    0,，
ln  x1 
1 x 1
不等式 f  x  x1就是不等式  x1（*），
2 ln  x1  2
2x
当1 x0时，（*）式等价于ln  x1  ；
x2
2x
当x0时，（*）式等价于ln  x1  ．
x2
2x 1 4 x2
设h  x ln  x1  ，h x    0，
x2 x1  x2 2  x1  x2 2
故h  x 在1,上单调递增，
2x
故当1 x0时，h  x h  0 0，即ln  x1  ，
x2
2x
当x0时，h  x h  0 0，即ln  x1  ．
x2
所以原式成立．
ta
（Ⅲ）设t  xa，令g  t  ，
lnt
f

x
既有极大值又有极小值等价于g 
t
既有极大值又有极小值．
ta
lnt
ta a
g t  t ，记s  t lnt lnt 1．
ln2t t t1 a ta
s t    ，
t t2 t2
①当a0时，有s
t
0，则s 
t
在
0,1


 1,上单调递增，
故函数s  t 在 0,1    1,上至多有1个零点，不合题意；
②当a 1时，s  t 在 0,1 上单调递减，在 1,上单调递增，且s  1 0，
故s  t 在 0,1    1,上没有零点，不合题意；
③当a 1时，s  t 在 0,1    1,a 上单调递减，在 a,上单调递增，
又s  1 a10，s  a lna 0，故函数s  t 在 0,1    1,上没有零点，不合题意；
④当0a1时，s  t 在 0,a 上单调递减，在 a,1    1,上单调递增，
a a
且有s  e lne 1 0 ，s  1 a10，s  a lna 0，
e e
 1 2 2 1 2  2 12  2 2
se aaea  a1 1  1  （这里用不等式：当 x0 时，
  a  a 2a   a
x2
ex 1x ）
2
a 4 4 2 a
2  1    0 ．
2a2 a a 2
 2
所以s  e s  1 0，s  a se
1
a0，
 
又因为函数s  t 的图象分别在区间 0,1 ， 1,上连续，
 2 
所以函数s  t 在e
1
a,a， 1,e 内各有1个零点，分别记为t 和t ，
1 2
 
故t 、t 分别为函数g  t 的极大值点、极小值点．即 f  x 既有极大值又有极小值．
1 2
综上，当0a1时， f  x 既有极大值又有极小值．
（用参数分离法求解本小题也给分）
19．（本小题满分17分）
解：（I）设X表示游程的个数，则X  2,3,4,5 ，由2个0和3个1在排列时，共有C2 10种排列，
5
当X 2时，有2种排列：11100、00111；
当X 3时，有3种排列：10011、11001、01110；
当X 4时，有4种排列：10110、11010、01011、01101；
当X 5时，只有一种排列：10101．
故X的分布列为：
X 2 3 4 5
2 3 4 1
P
10 10 10 10
2 3 4 1 17
期望为EX 2 3 4 5  ．
10 10 10 10 5
Cn1 n
（Ⅱ）（i）P  A  mn1  ，
1 Cn mn
mn
Cn1 mn
P  A  mn2  ．
2 Cn  mn  mn1 
mn
1,A发生
（ii）可知当随机事件A 发生时，a 就是一个1游程的开始，此时令I  k ，
k k A k 0,A不发生
k
mn
设1游程个数为Y，则Y  I ，
A
k
k1
Cn1 n Cn1 mn
由（i）可知P  A  mn1  ，P  A  mn2  ，k 2，3，…，
1 Cn mn k Cn  mn  mn1 
mn mn
mn，
mn  mn mn
由期望的性质可知，EY  E I   EI  P  A 
A A k
 k  k
k1 k1 k1
n mn mn n mn
   ，
mn  mn  mn1  mn
k2
mmn
设0游程个数为Z，类似可得EZ  ，
mn
mn2mn 2mn
因此两类游程数目的数学期望为E  Y Z  1 ．
mn mn