文档内容
2024-2025(上)8 月月度质量监测暨第零次诊断测试
高 三 数 学 参考答案及解析
【命题单位:辽宁沈文新高考研究联盟】
1 2 3 4 5 6 7 8 9 10 11
D A D B B D A D ACD AC ABD
1.
【详解】因为集合 , ,
所以 ,
𝑀𝑀 ={0,1,2,3,4} 𝑁𝑁 ={1,3,5}
所以集合 的子集为 ,共四个.
𝑃𝑃 =𝑀𝑀∩𝑁𝑁 ={1,3}
2.
𝑃𝑃 ∅,{1},{3},{1,3}
2+ 2i 2+ 2i 2
z = = = = 2
1−i 1−i 2
【详解】由 ,可得 ,
√2+√2𝑖𝑖
3.
𝑧𝑧 = 1−𝑖𝑖
【详解】在椭圆 中, , ,则c= a2−b2 =2,
2 2
𝑥𝑥 𝑦𝑦
5 + 9 =1 𝑎𝑎 =3 𝑏𝑏 =√5
易知该椭圆的焦点在 轴上,因此,椭圆 的焦点的坐标为 , .
2 2
𝑥𝑥 𝑦𝑦
4. 𝑦𝑦 5 + 9 =1 (0,−2) (0,2)
【详解】解:根据题意,先在14个球种取出1个球放到编号为2的盒子里,再取出2个球
放在编号为3的盒子里,
此时只需将剩下的11个球,分为3组,每组至少一个,分别放到三个盒子里即可;
将11个球排成一列,排好后,有10个空位,
C2 =45
在10个空位中任取2个,插入挡板,有 10 种方法,即有45种将11个球分为3组的
方法,
将分好的3组对应3个盒子,即可满足盒内的球数不小于盒号数,
则盒内的球数不小于盒号数的放入方法有45种,
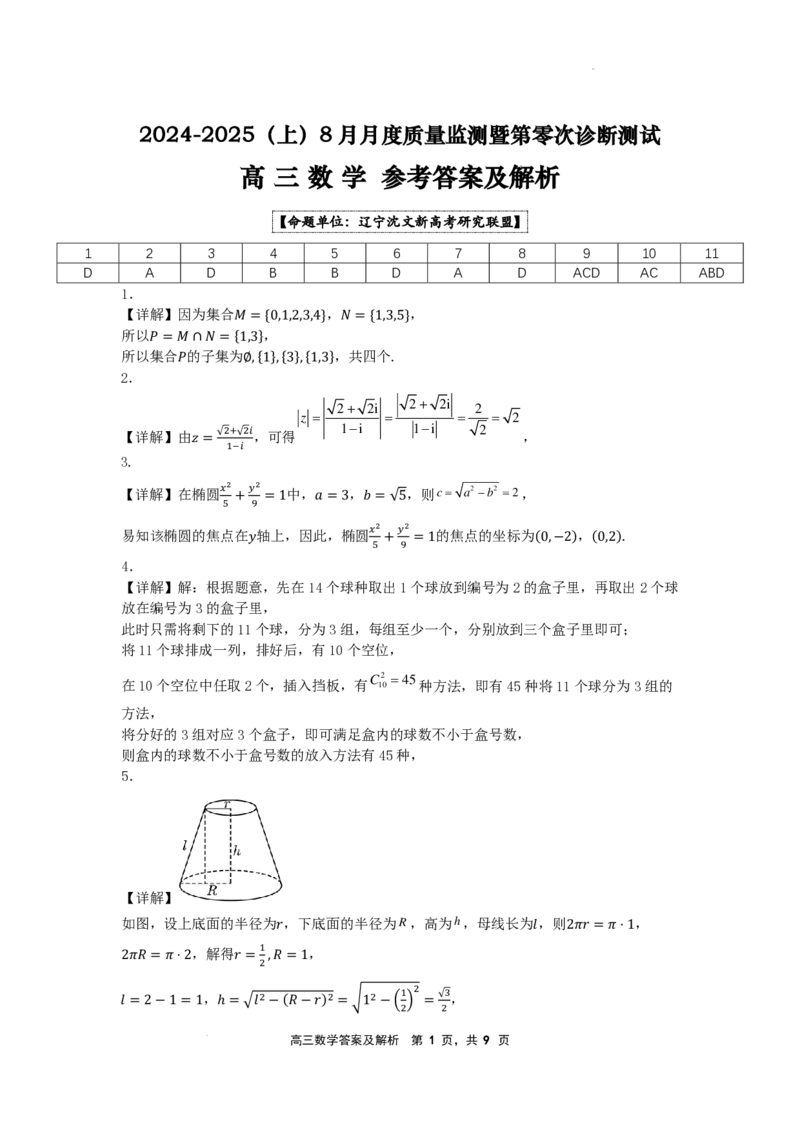
5.
【详解】
如图,设上底面的半径为 ,下底面的半径为R,高为h,母线长为 ,则 ,
,解得 𝑟𝑟 , 𝑙𝑙 2𝜋𝜋𝑟𝑟 =𝜋𝜋⋅1
1
2𝜋𝜋𝜋𝜋 =𝜋𝜋⋅2 𝑟𝑟 =2,𝜋𝜋 =1
, ,
2 2 2
1 2 √3
𝑙𝑙 =2−1=1 ℎ =�𝑙𝑙 −(𝜋𝜋−𝑟𝑟) =�1 −�2� = 2
高三数学答案及解析 第 1 页,共 9 页
学科网(北京)股份有限公司设上底面面积为 ,下底面面积为 ,
′ 1 2 𝜋𝜋 2
𝑆𝑆 =𝜋𝜋⋅�2� = 4 𝑆𝑆 =𝜋𝜋⋅1 =𝜋𝜋
则体积为 .
1 ′ ′ 1 𝜋𝜋 𝜋𝜋 √3 7√3𝜋𝜋
6. 3�𝑆𝑆+𝑆𝑆 +√𝑆𝑆𝑆𝑆 �ℎ=3�𝜋𝜋+4+2�⋅ 2 = 24
【详解】因为函数 为R上的奇函数,所以 ,
又当 时, ,所以 ,
𝑓𝑓(𝑥𝑥) 𝑓𝑓(0)=0
所以 ,
𝑥𝑥 >0 𝑓𝑓(𝑥𝑥)=2𝑥𝑥−1 𝑓𝑓(−1)=−𝑓𝑓(1)=−(2×1−1)=−1
故选:D.
𝑓𝑓(0)+𝑓𝑓(−1)=0+(−1)=−1
7.
【详解】 , ,且 ,
1 1 1
∵𝑎𝑎𝑛𝑛+1−𝑎𝑎𝑛𝑛+𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1 =0 ∴𝑎𝑎𝑛𝑛+1−𝑎𝑎𝑛𝑛 =1 𝑎𝑎1 =2
所以数列 是首项为2,公差为1的等差数列,所以 ,
1 1
�𝑎𝑎𝑛𝑛� 𝑎𝑎𝑛𝑛 =2+(𝑛𝑛−1)=𝑛𝑛+1
即 ,
1 1 1 1
𝑎𝑎𝑛𝑛 =𝑛𝑛+1 𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1 =(𝑛𝑛+1)(𝑛𝑛+2)=𝑛𝑛+1−𝑛𝑛+2
1 1 1 1 1 1 1 1
𝑆𝑆100 =2−3+3−4+4−5+...+101−102
.
1 1 25
=8.2 −102=51
【详解】对于A,由已知得 ,即
1 1
𝑓𝑓(𝜋𝜋−𝑥𝑥)=𝑠𝑠𝑠𝑠𝑛𝑛(𝜋𝜋−𝑥𝑥)+2𝑠𝑠𝑠𝑠𝑛𝑛2(𝜋𝜋−𝑥𝑥)=𝑠𝑠𝑠𝑠𝑛𝑛𝑥𝑥−2𝑠𝑠𝑠𝑠𝑛𝑛2𝑥𝑥
,故 不关于 对称,故A错误;
𝜋𝜋
𝑓𝑓(𝜋𝜋−𝑥𝑥)≠𝑓𝑓(𝑥𝑥) 𝑓𝑓(𝑥𝑥) 𝑥𝑥 = 2
对于B, ,故B错误;
3𝜋𝜋 3𝜋𝜋 1
对于C,𝑓𝑓利�用2二�=倍𝑠𝑠角𝑠𝑠𝑛𝑛公2式+知2𝑠𝑠𝑠𝑠𝑛𝑛3𝜋𝜋 =−1≠0 ,令 得 或
,即 ,所以该函数在区间 内有4个零点,故C错误;
𝑓𝑓(𝑥𝑥)=𝑠𝑠𝑠𝑠𝑛𝑛𝑥𝑥(1+𝑐𝑐𝑐𝑐𝑠𝑠𝑥𝑥) 𝑓𝑓(𝑥𝑥)=0 𝑠𝑠𝑠𝑠𝑛𝑛𝑥𝑥 =0 𝑐𝑐𝑐𝑐𝑠𝑠𝑥𝑥 =
−对1于D,𝑥𝑥求=导𝑘𝑘𝜋𝜋(𝑘𝑘 ∈𝑍𝑍) [0,10] ,令cosx=t,由 ,知
′ 2 5𝜋𝜋 7𝜋𝜋
,即
𝑓𝑓
g(
(
t
𝑥𝑥
)
)
=
=
2t
𝑐𝑐
2
𝑐𝑐
+
𝑠𝑠
t
𝑥𝑥
−
+
1,
𝑐𝑐𝑐𝑐
利
𝑠𝑠2
用
𝑥𝑥
二
=
次
2
函
𝑐𝑐𝑐𝑐
数
𝑠𝑠
性
𝑥𝑥
质
+
知
𝑐𝑐𝑐𝑐𝑠𝑠𝑥𝑥−1
,即 ,
𝑥𝑥
可
∈
知
�3 , 3�
在区
1 ′
𝑡𝑡 ∈�2,1� 𝑔𝑔(𝑡𝑡)≥0 𝑓𝑓 (𝑥𝑥)≥0 𝑓𝑓(𝑥𝑥)
间 上单调递增,故D正确;
5𝜋𝜋 7𝜋𝜋
9.𝑥𝑥 ∈�3 , 3�
【详解】对于A,极差为 ,中位数为 ,所以极差与中位数之积为
1+2 3
3 4−0=4 2 =2
4× =6
2 ,A对;
对于B,根据方差的性质可知,数据 的方差是 ,B
错; 2
4𝑥𝑥1−1,4𝑥𝑥2−1,⋯,4𝑥𝑥𝑛𝑛−1 4 ×5=80
对于C,由方差 ,
2 1 2 2 2
𝑠𝑠 =𝑛𝑛[(𝑥𝑥1−𝑥𝑥̄) +(𝑥𝑥2−𝑥𝑥̄) +⋯(𝑥𝑥𝑛𝑛−𝑥𝑥̄) ]=0
高三数学答案及解析 第 2 页,共 9 页
学科网(北京)股份有限公司可得 ,即此组数据众数唯一,C对;
对于𝑥𝑥D1,=𝑥𝑥2 =⋯=𝑥𝑥𝑛𝑛 =𝑥𝑥̄ ,
𝑥𝑥1+𝑥𝑥2+⋯+𝑥𝑥𝑛𝑛
∵ 𝑛𝑛 =𝑥𝑥0,∴𝑥𝑥1+𝑥𝑥2+⋯+𝑥𝑥𝑛𝑛 =𝑛𝑛𝑥𝑥0
,D对.
𝑥𝑥0+𝑥𝑥1+𝑥𝑥2+⋯+𝑥𝑥𝑛𝑛 𝑥𝑥0+𝑛𝑛𝑥𝑥0
∴10. 𝑛𝑛+1 = 𝑛𝑛+1 =𝑥𝑥0
【详解】A选项,依题意,抛物线 的准线方程为 ,即 ,所以 ,
𝑝𝑝
即抛物线 的方程为 ,则抛𝐶𝐶物线 的焦点为𝑥𝑥 =−.2 𝑥𝑥 =−2 =−2 𝑝𝑝=4
设直线 的方程为 2 , , ,
𝐶𝐶 𝑦𝑦 =8𝑥𝑥 𝐶𝐶 (2,0)
联立 𝑙𝑙 消𝑥𝑥 =去𝑡𝑡𝑦𝑦整+理2得𝐴𝐴(𝑥𝑥1,𝑦𝑦1) 𝐵𝐵(𝑥𝑥2,𝑦𝑦2) 恒成立,
𝑥𝑥 =𝑡𝑡𝑦𝑦+2, 2 2
则 � 2 𝑥𝑥 ,𝑦𝑦 −8𝑡𝑡𝑦𝑦−16=0,𝛥𝛥 =64𝑡𝑡 +64>0
𝑦𝑦 =8𝑥𝑥,
则𝑦𝑦1+𝑦𝑦2 =8𝑡𝑡,𝑦𝑦1𝑦𝑦2 =−16 , ,
2
2
(𝑦𝑦1𝑦𝑦2)
𝑥𝑥1+𝑥𝑥2 =𝑡𝑡(𝑦𝑦1+𝑦𝑦2)+4=8𝑡𝑡 +4 𝑥𝑥1𝑥𝑥2 = 64 =4
又因为线段 为 的直径, 与 的准线相切于点P(−2,−1),
所以 𝐴𝐴𝐵𝐵 ⊙𝐷𝐷 ⊙𝐷𝐷 𝐶𝐶
,
𝐴𝐴����𝑃𝑃�⃗⋅𝐵𝐵����𝑃𝑃�⃗ =(−2−𝑥𝑥1,−1−𝑦𝑦1)⋅(−2−𝑥𝑥2,−1−𝑦𝑦2)
整=理(2得+4𝑥𝑥1+)2(2 (x+
1
+𝑥𝑥2x)
2
) ++(x1
1
x+
2
+𝑦𝑦11+)(1+𝑦𝑦2)=0
,
即 𝑦𝑦1+𝑦𝑦2+ , 𝑦𝑦1 𝑦𝑦2 =0
2
即4(4+t+ 21()8 2 𝑡𝑡 =0+,4解)+得4+1+,8𝑡𝑡所−以16直=线0的方程为4x+y−8=0,所以A正确;
1
𝑡𝑡 =−4 𝑙𝑙
B选项,因为 垂直于准线,且P(−2,−1),所以点 的纵坐标为−1,
代入直线 的方
𝐷𝐷
程
𝑃𝑃 4x+y−8=0,即
,
𝐷𝐷
解得 ,
9
𝑙𝑙 4𝑥𝑥−1−8=0 𝑥𝑥 =4
可得点 ,所以B错误;
9
𝐷𝐷�4,−1�
17
|AB|=x +x +4=
C选项,根据抛物线的定义可得 1 2 2 ,所以 的半径为 ,
17
⊙𝐷𝐷 4
所以 的周长为 ,所以C选项正确;
17
⊙𝐷𝐷 2 𝜋𝜋
4x+2y+9=0
D选项,圆心 到直线 的距离为 ,
9
9 �4×4−2+9� 8√5 17
4x+𝐷𝐷 2 � y4+, 9 −=1� 0 2√5 = 5 < 4
所以直线 与 相交,不相切,所以D错误.
11.
⊙𝐷𝐷
【详解】对于A,由题意得 ,则 ,
𝑙𝑙𝑛𝑛𝑥𝑥 ′ 1−𝑙𝑙𝑛𝑛𝑥𝑥
当 时, 𝑓𝑓,(𝑥𝑥)=递𝑥𝑥增 ,𝑓𝑓当(𝑥𝑥)= 时𝑥𝑥 2, , 递减,
′ ′
0<𝑥𝑥 <𝑒𝑒 𝑓𝑓 (𝑥𝑥)>0 𝑓𝑓(𝑥𝑥) 𝑥𝑥 >𝑒𝑒 𝑓𝑓 (𝑥𝑥)<0 𝑓𝑓(𝑥𝑥)
高三数学答案及解析 第 3 页,共 9 页
学科网(北京)股份有限公司由于 ,所以 ,即 ,
𝑙𝑙𝑛𝑛4 2𝑙𝑙𝑛𝑛2 𝑙𝑙𝑛𝑛2 𝑙𝑙𝑛𝑛√11
整理𝑒𝑒得<√11<4 𝑓𝑓(,4)即<𝑓𝑓�√11� 4,=所以4 = 2 < √11 ,故正确;
对于B,由于 ,由于当 √时11, 递减,故 √11 ,√ 2
√11𝑙𝑙𝑛𝑛2<2𝑙𝑙𝑛𝑛√11 𝑙𝑙𝑛𝑛2 <𝑙𝑙𝑛𝑛11 2 <11<11
lnπ
即 3π2 3ln𝑥𝑥π>,𝑒𝑒即 𝑓𝑓(𝑥𝑥) ,𝑓𝑓 (3)>𝑓𝑓(𝜋𝜋)
𝑙𝑙𝑛𝑛3 𝜋𝜋 2
3 > 𝜋𝜋 ,2 × 2𝑙𝑙𝑛𝑛3 >3𝑙𝑙𝑛𝑛𝜋𝜋
因为 ,
𝑙𝑙𝑛𝑛2 𝑙𝑙𝑛𝑛4
𝑓𝑓(2) ln = π 2 = 4 =𝑓𝑓(4)<𝑓𝑓(𝜋𝜋)
故 πln2<3 2lnπ,即 ,
𝑙𝑙𝑛𝑛2 2 𝜋𝜋
综上2,< 𝜋𝜋 ,3 × ,3故𝑙𝑙𝑛𝑛B𝜋𝜋正确>;3𝑙𝑙 𝑛𝑛2
𝜋𝜋 2 𝜋𝜋
对于C,2𝑙𝑙因𝑛𝑛为3 >3𝑙𝑙𝑛𝑛𝜋𝜋 >3𝑙𝑙𝑛𝑛2 ,即 x 1 lnx 2 =x 2 lnx 1,即
𝑥𝑥1 𝑥𝑥2 𝑥𝑥1 𝑥𝑥2
𝑥𝑥2 =𝑥𝑥1 ⇒𝑙𝑙𝑛𝑛𝑥𝑥2 =𝑙𝑙𝑛𝑛𝑥𝑥1
lnx lnx
1 = 2 , f(x )= f(x )
x x 1 2
1 2 ,
设 ,由于当 时, 递增 ,当 时,
递减,
𝑔𝑔(𝑡𝑡)=𝑓𝑓(𝑒𝑒+𝑡𝑡)−𝑓𝑓(𝑒𝑒−𝑡𝑡),𝑡𝑡 ∈(0,𝑒𝑒) 0<𝑥𝑥 <𝑒𝑒 𝑓𝑓(𝑥𝑥) 𝑥𝑥 >𝑒𝑒
故𝑓𝑓(𝑥𝑥) 单调减函数,故g(t)e2 ⇔lnx +lnx >2⇔m(x +x )>2⇔ 1 2 >
1 2 1 2 1 2 x −x x +x
1 2 1 2
x
2( 1 −1)
2(x −x ) x x
⇔lnx −lnx > 1 2 ⇔ln 1 > 2
1 2 x +x x x
1 2 2 1 +1
x
2 ,
x 2(t−1) 1 2(t+1)−2(t−1) (t−1)2
t = 1 >1, u(t)=lnt− u′(t)= − = >0
设 x 2 令 t+1 ,则 t (t+1)2 t(t+1)2 ,
2(t−1)
u(t)=lnt− ,(t >1)
即 t+1 为单调增函数,故 ,
即
𝑥𝑥1
成立,故 ,所以 𝑢𝑢(𝑡𝑡)>𝑢𝑢(1)=,0即 ,故D正
确𝑙𝑙,𝑛𝑛 𝑥𝑥 𝑥𝑥 1 2 > 2( 𝑥𝑥 𝑥𝑥 𝑥𝑥 1 2 2 + − 1 1) 𝑥𝑥1𝑥𝑥2 >𝑒𝑒 2 𝑙𝑙𝑛𝑛(𝑥𝑥1𝑥𝑥2)>𝑙𝑙𝑛𝑛𝑒𝑒 2 𝑙𝑙𝑛𝑛𝑥𝑥1+𝑙𝑙𝑛𝑛𝑥𝑥2 >2
12. /
3
−5 −0.6
高三数学答案及解析 第 4 页,共 9 页
学科网(北京)股份有限公司【详解】因为sin sin cos 为锐角,
4 2 2
𝛼𝛼 =5, 𝛼𝛼+ 𝛼𝛼 =1,𝛼𝛼
所以cos ,则cos cos .
3 3
13. 𝛼𝛼 =5 (𝜋𝜋+𝛼𝛼)=− 𝛼𝛼 =−5
【详解】因为 , ,
所以 𝑎𝑎⃗ =�√3,3� 𝑏𝑏�⃗=(−2,0)
2
𝑎𝑎⃗⋅𝑏𝑏�⃗ =−2√3,�𝑏𝑏�⃗� =4
在 上的投影向量为 ,
𝑏𝑏�⃗ 𝑎𝑎�⃗⋅𝑏𝑏�⃗ 𝑏𝑏�⃗ 𝑎𝑎�⃗⋅𝑏𝑏�⃗ −2√3
1𝑎𝑎⃗4.𝑏𝑏�⃗①②③④ |𝑎𝑎⃗|𝑐𝑐𝑐𝑐𝑠𝑠�𝑎𝑎⃗,𝑏𝑏�⃗��𝑏𝑏�⃗�=|𝑎𝑎⃗|⋅|𝑎𝑎�⃗|�𝑏𝑏�⃗�⋅�𝑏𝑏�⃗�=�𝑏𝑏�⃗� 2 ⋅𝑏𝑏�⃗= 4 (−2,0)=�√3,0�
【详解】解:因为 , ,
所以 𝐴𝐴𝐵𝐵 =𝐵𝐵𝐶𝐶 =2 𝐴𝐴,𝐶𝐶 =2√3
2 2 2
2 +2 −�2√3� 1
𝑐𝑐𝑐𝑐𝑠𝑠∠𝐴𝐴𝐵𝐵𝐶𝐶 = 2×2×2 =−2
所以 ,
2𝜋𝜋
因为∠平𝐴𝐴面𝐵𝐵𝐶𝐶 = 3 平面 ,平面 平面ABC =BC, ,
所以 平面 , ,
𝐵𝐵𝐶𝐶𝐷𝐷 ⊥ 𝐴𝐴𝐵𝐵𝐶𝐶 𝐵𝐵𝐶𝐶𝐷𝐷∩ 𝐷𝐷𝐵𝐵 ⊥𝐵𝐵𝐶𝐶
又 平面 ,所以平面 平面 ,所以①②正确;
𝐷𝐷𝐵𝐵 ⊥ 𝐴𝐴𝐵𝐵𝐶𝐶 𝐷𝐷𝐵𝐵 ⊥𝐴𝐴𝐶𝐶
𝐷𝐷𝐵𝐵 ⊂ 𝐷𝐷𝐴𝐴𝐵𝐵 𝐷𝐷𝐴𝐴𝐵𝐵1⊥1 𝐴𝐴𝐵𝐵𝐶𝐶 2π 4 3
× ×2×2×sin ×4=
进一步三棱锥 的体积为3 2 3 3 ,所以③正确;
设三角形 的𝐷𝐷外−𝐴𝐴心𝐵𝐵为𝐶𝐶 ,过 作 平面 ,
则三角形𝐴𝐴𝐵𝐵𝐶𝐶的外接圆𝐹𝐹的半径𝐹𝐹为 𝐹𝐹𝐹𝐹 ⊥ 𝐴𝐴𝐵𝐵,𝐶𝐶
1 2√3
2𝜋𝜋
设 为三棱𝐴𝐴𝐵𝐵锥𝐶𝐶 外接球的球2心×𝑠𝑠,𝑖𝑖𝑛𝑛 3 =2
则 , ,所以 ,
𝐹𝐹 𝐷𝐷−𝐴𝐴𝐵𝐵𝐶𝐶
所以 ,解2得 2 , 2 2
𝐹𝐹𝐴𝐴=𝐹𝐹𝐵𝐵 =2 𝐹𝐹𝐴𝐴=𝐹𝐹𝐷𝐷 √𝐹𝐹𝐴𝐴 +𝐹𝐹𝐹𝐹 =�𝐹𝐹𝐵𝐵 +(𝐷𝐷𝐵𝐵−𝐹𝐹𝐹𝐹)
所以外接2 球的半2 径为2 2 ,
√2 +𝐹𝐹𝐹𝐹 =�2 +(4−𝐹𝐹𝐹𝐹) 𝐹𝐹𝐹𝐹 =2
2 2
所以三棱锥 的𝐹𝐹𝐴𝐴外=接√球2的+表𝐹𝐹面𝐹𝐹积=为24√π2⋅OA2 =32π,所以④正确.
𝐷𝐷−𝐴𝐴𝐵𝐵𝐶𝐶
15.(1) ;(2) ;(3)
1 7 3
【详解】4(1)设244名同8学的书包分别为A,B,C,D,4名同学拿书包的所有可能可表示为
, , , , , ,
, , , , , ,
(𝐴𝐴,𝐵𝐵,𝐶𝐶,𝐷𝐷) (𝐴𝐴,𝐵𝐵,𝐷𝐷,𝐶𝐶) (𝐴𝐴,𝐶𝐶,𝐵𝐵,𝐷𝐷) (𝐴𝐴,𝐶𝐶,𝐷𝐷,𝐵𝐵) (𝐴𝐴,𝐷𝐷,𝐵𝐵,𝐶𝐶) (𝐴𝐴,𝐷𝐷,𝐶𝐶,𝐵𝐵)
, , , , , ,
(𝐵𝐵,𝐴𝐴,𝐶𝐶,𝐷𝐷) (𝐵𝐵,𝐴𝐴,𝐷𝐷,𝐶𝐶) (𝐵𝐵,𝐶𝐶,𝐴𝐴,𝐷𝐷) (𝐵𝐵,𝐶𝐶,𝐷𝐷,𝐴𝐴) (𝐵𝐵,𝐷𝐷,𝐴𝐴,𝐶𝐶) (𝐵𝐵,𝐷𝐷,𝐶𝐶,𝐴𝐴)
, , , , , ,
(𝐶𝐶,𝐴𝐴,𝐵𝐵,𝐷𝐷) (𝐶𝐶,𝐴𝐴,𝐷𝐷,𝐵𝐵) (𝐶𝐶,𝐵𝐵,𝐴𝐴,𝐷𝐷) (𝐶𝐶,𝐵𝐵,𝐷𝐷,𝐴𝐴) (𝐶𝐶,𝐷𝐷,𝐴𝐴,𝐵𝐵) (𝐶𝐶,𝐷𝐷,𝐵𝐵,𝐴𝐴)
共有24种情况.
(𝐷𝐷,𝐴𝐴,𝐵𝐵,𝐶𝐶) (𝐷𝐷,𝐴𝐴,𝐶𝐶,𝐵𝐵) (𝐷𝐷,𝐵𝐵,𝐴𝐴,𝐶𝐶) (𝐷𝐷,𝐵𝐵,𝐶𝐶,𝐴𝐴) (𝐷𝐷,𝐶𝐶,𝐴𝐴,𝐵𝐵) (𝐷𝐷,𝐶𝐶,𝐵𝐵,𝐴𝐴)
恰有两名同学拿对了书包包含6个样本点,分别为
, , , , , ,
故(𝐴𝐴其,𝐵𝐵概,𝐷𝐷率,𝐶𝐶为) (𝐴𝐴,𝐶𝐶,𝐵𝐵,𝐷𝐷.) (𝐴𝐴,𝐷𝐷,𝐶𝐶,𝐵𝐵) (𝐵𝐵,𝐴𝐴,𝐶𝐶,𝐷𝐷) (𝐶𝐶,𝐵𝐵,𝐴𝐴,𝐷𝐷) (𝐷𝐷,𝐵𝐵,𝐶𝐶,𝐴𝐴)
6 1
(2)至少有𝑃𝑃两=名24同=学4拿对了书包包含7个样本点,分别为
高三数学答案及解析 第 5 页,共 9 页
学科网(北京)股份有限公司, , , , , , ,
故(𝐴𝐴其,𝐵𝐵概,𝐶𝐶率,𝐷𝐷为) (𝐴𝐴,𝐵𝐵,.𝐷𝐷 ,𝐶𝐶) (𝐴𝐴,𝐶𝐶,𝐵𝐵,𝐷𝐷) (𝐴𝐴,𝐷𝐷,𝐶𝐶,𝐵𝐵) (𝐵𝐵,𝐴𝐴,𝐶𝐶,𝐷𝐷) (𝐶𝐶,𝐵𝐵,𝐴𝐴,𝐷𝐷) (𝐷𝐷,𝐵𝐵,𝐶𝐶,𝐴𝐴)
7
(3)书包都𝑃𝑃拿=错24了包含9个样本点,分别为
, , , , , ,
, , ,
(𝐵𝐵,𝐴𝐴,𝐷𝐷,𝐶𝐶) (𝐵𝐵,𝐶𝐶,𝐷𝐷,𝐴𝐴) (𝐵𝐵,𝐷𝐷,𝐴𝐴,𝐶𝐶) (𝐶𝐶,𝐴𝐴,𝐷𝐷,𝐵𝐵) (𝐶𝐶,𝐷𝐷,𝐴𝐴,𝐵𝐵) (𝐶𝐶,𝐷𝐷,𝐵𝐵,𝐴𝐴)
(故𝐷𝐷其,𝐴𝐴概,𝐵𝐵率,𝐶𝐶为) (𝐷𝐷,𝐶𝐶,𝐴𝐴,𝐵𝐵.) (𝐷𝐷,𝐶𝐶,𝐵𝐵,𝐴𝐴)
9 3
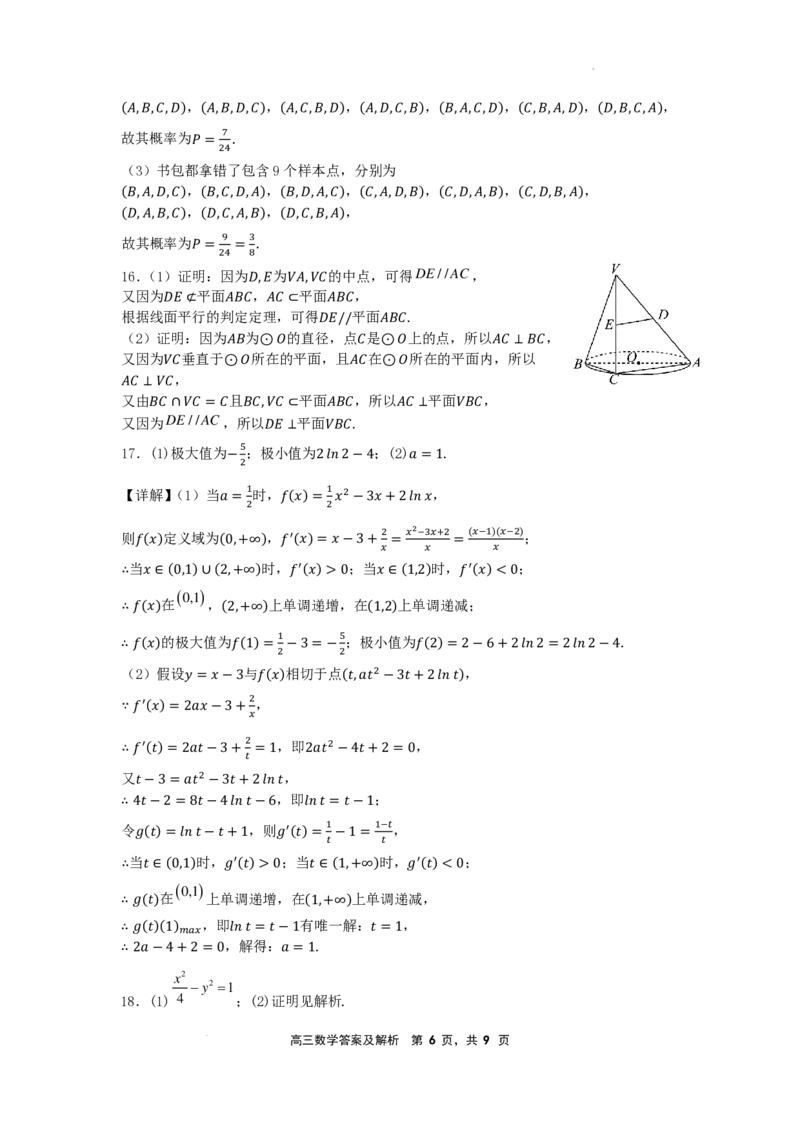
16.(1)证𝑃𝑃明=:2因4为=8 为 的中点,可得DE//AC,
又因为 平面 , 平面 ,
𝐷𝐷,𝐸𝐸 𝑉𝑉𝐴𝐴,𝑉𝑉𝐶𝐶
根据线面平行的判定定理,可得 平面 .
𝐷𝐷𝐸𝐸 ⊄ 𝐴𝐴𝐵𝐵𝐶𝐶 𝐴𝐴𝐶𝐶 ⊂ 𝐴𝐴𝐵𝐵𝐶𝐶
(2)证明:因为 为 的直径,点 是 上的点,所以 ,
𝐷𝐷𝐸𝐸// 𝐴𝐴𝐵𝐵𝐶𝐶
又因为 垂直于 所在的平面,且 在 所在的平面内,所以
𝐴𝐴𝐵𝐵 ⊙𝐹𝐹 𝐶𝐶 ⊙𝐹𝐹 𝐴𝐴𝐶𝐶 ⊥𝐵𝐵𝐶𝐶
,
𝑉𝑉𝐶𝐶 ⊙𝐹𝐹 𝐴𝐴𝐶𝐶 ⊙𝐹𝐹
又由 且 平面 ,所以 平面 ,
𝐴𝐴𝐶𝐶 ⊥𝑉𝑉𝐶𝐶
又因为DE//AC,所以 平面 .
𝐵𝐵𝐶𝐶∩𝑉𝑉𝐶𝐶 =𝐶𝐶 𝐵𝐵𝐶𝐶,𝑉𝑉𝐶𝐶 ⊂ 𝐴𝐴𝐵𝐵𝐶𝐶 𝐴𝐴𝐶𝐶 ⊥ 𝑉𝑉𝐵𝐵𝐶𝐶
17.(1)极大值为 ;极𝐷𝐷小𝐸𝐸 ⊥值为 𝑉𝑉𝐵𝐵𝐶𝐶 ;(2) .
5
−2 2𝑙𝑙𝑛𝑛2−4 𝑎𝑎=1
【详解】(1)当 时, ,
1 1 2
𝑎𝑎 =2 𝑓𝑓(𝑥𝑥)=2𝑥𝑥 −3𝑥𝑥+2𝑙𝑙𝑛𝑛𝑥𝑥
则 定义域为 , ;
2
′ 2 𝑥𝑥 −3𝑥𝑥+2 (𝑥𝑥−1)(𝑥𝑥−2)
当𝑓𝑓(𝑥𝑥) (0,+∞)时,𝑓𝑓 (𝑥𝑥)=𝑥𝑥−;3当+𝑥𝑥 = 𝑥𝑥时,= 𝑥𝑥 ;
′ ′
∴ 𝑥𝑥 ∈在(0
( ,01,)1)
∪,(2,+∞) 上单𝑓𝑓调(𝑥𝑥递)增>,0 在 𝑥𝑥 ∈上(1单,2)调递减𝑓𝑓;(𝑥𝑥 )<0
∴𝑓𝑓(𝑥𝑥)
的极大值为
(2,+∞)
;极
(1小,2值 )
为 .
1 5
∴(𝑓𝑓2()𝑥𝑥)假设 𝑓𝑓(与1)=2相−切3=于−点2 𝑓𝑓(2)=2,− 6+2𝑙𝑙𝑛𝑛2=2𝑙𝑙𝑛𝑛2−4
2
𝑦𝑦=𝑥𝑥−3 ,𝑓𝑓( 𝑥𝑥) (𝑡𝑡,𝑎𝑎𝑡𝑡 −3𝑡𝑡+2𝑙𝑙𝑛𝑛𝑡𝑡)
′ 2
∵𝑓𝑓 (𝑥𝑥)=2𝑎𝑎𝑥𝑥−3+𝑥𝑥
,即 ,
′ 2 2
∴又𝑓𝑓 (𝑡𝑡)=2𝑎𝑎𝑡𝑡−3+𝑡𝑡 =1 , 2𝑎𝑎𝑡𝑡 −4𝑡𝑡+2=0
2 ,即 ;
𝑡𝑡−3=𝑎𝑎𝑡𝑡 −3𝑡𝑡+2𝑙𝑙𝑛𝑛𝑡𝑡
∴令4𝑡𝑡−2=8𝑡𝑡−4𝑙𝑙𝑛𝑛𝑡𝑡,−则6 𝑙𝑙𝑛𝑛𝑡𝑡 =𝑡𝑡−1 ,
′ 1 1−𝑡𝑡
当𝑔𝑔(𝑡𝑡)=𝑙𝑙𝑛𝑛𝑡𝑡时−,𝑡𝑡+1 𝑔𝑔;(当𝑡𝑡)= 𝑡𝑡 −1= 时𝑡𝑡 , ;
′ ′
∴ 𝑡𝑡 ∈在(0
( ,01,)1)
上单𝑔𝑔调(𝑡𝑡递)>增0,在 𝑡𝑡 ∈(1,+上∞单)调递𝑔𝑔减(,𝑡𝑡) <0
,即 有唯一解: ,
∴𝑔𝑔(𝑡𝑡) (1,+∞)
,解得: .
∴𝑔𝑔(𝑡𝑡)(1)𝑚𝑚𝑎𝑎𝑥𝑥 𝑙𝑙𝑛𝑛𝑡𝑡 =𝑡𝑡−1 𝑡𝑡 =1
∴2𝑎𝑎−4x+2 2=0 𝑎𝑎 =1
−y2 =1
18.(1) 4 ;(2)证明见解析.
高三数学答案及解析 第 6 页,共 9 页
学科网(北京)股份有限公司【详解】(1)依题意,设双曲线C的方程为 ,而点 在双曲线
2 2
𝑥𝑥 𝑦𝑦
C上, 12− 3 =𝜆𝜆(𝜆𝜆 ≠0) 𝐴𝐴(2√2,−1)
x2
−y2 =1
于是 ,双曲线C的方程为 ,即 4 ,
2 2 2 2
(2√2) (−1) 1 𝑥𝑥 𝑦𝑦 1
𝜆𝜆 = 12 − 3 =3 12− 3 =3
x2
−y2 =1
所以双曲线C的标准方程为 4 .
(2)当直线 斜率存在时,设直线 的方程为: ,设 ,
由 𝐸𝐸𝐹𝐹 消去y并整理得 𝐸𝐸𝐹𝐹 𝑦𝑦=𝑘𝑘𝑥𝑥+𝑚𝑚 𝐸𝐸(𝑥𝑥,1, 𝑦𝑦1),𝐹𝐹(𝑥𝑥2,𝑦𝑦2)
𝑦𝑦=𝑘𝑘𝑥𝑥+𝑚𝑚 2 2 2
有� 2 2 ,且 (4𝑘𝑘 −1)𝑥𝑥 +8𝑘𝑘𝑚𝑚𝑥𝑥+4(𝑚𝑚,即+1)=0 且
𝑥𝑥 −4𝑦𝑦 =4
2, 2 2 2 2 2 2
4𝑘𝑘 −1≠0 𝛥𝛥 =(8𝑘𝑘𝑚𝑚) −16(𝑚𝑚 +1)(4𝑘𝑘 −1)>0 4𝑘𝑘 −1≠0 4𝑘𝑘 −𝑚𝑚 −
1有<0 ,又
2
−8𝑘𝑘𝑚𝑚 4𝑚𝑚 +4 2
𝑥𝑥1+𝑥𝑥2 =4𝑘𝑘 2 −1,,𝑥𝑥1 𝑥𝑥2 = 4𝑘𝑘 2 −1 𝑦𝑦1𝑦𝑦2 =(𝑘𝑘𝑥𝑥1+𝑚𝑚)(𝑘𝑘𝑥𝑥2+𝑚𝑚)=𝑘𝑘 𝑥𝑥1𝑥𝑥2+
2 ,由 ,得 ,
𝑘𝑘𝑚𝑚(𝑥𝑥1+𝑥𝑥2)+𝑚𝑚
整理得 ,
𝐷𝐷����𝐸𝐸�⃗ =(𝑥𝑥1−2,𝑦𝑦1),𝐷𝐷����𝐹𝐹�⃗ =(𝑥𝑥2−2,𝑦𝑦2) 𝐷𝐷����𝐸𝐸�⃗·𝐷𝐷����𝐹𝐹�⃗ =0 (𝑥𝑥1−2)(𝑥𝑥2−2)+𝑦𝑦1𝑦𝑦2 =0
2 2
于是 (𝑘𝑘 +1)⋅𝑥𝑥1𝑥𝑥2+(𝑘𝑘𝑚𝑚−2)⋅(𝑥𝑥1+𝑥𝑥2)+𝑚𝑚 +4,=化0简得 ,
2
2 4𝑚𝑚 +4 −8𝑘𝑘𝑚𝑚 2 2 2
2 2
(𝑘𝑘 +1)⋅ 4𝑘𝑘 −1 +(𝑘𝑘𝑚𝑚−2)⋅4𝑘𝑘 −1+𝑚𝑚 +4=0 3𝑚𝑚 +16𝑘𝑘𝑚𝑚+20𝑘𝑘 =0
即 ,解得 或 ,均满足条件,
10
当(3𝑚𝑚+10时𝑘𝑘),(𝑚𝑚直+线2𝑘𝑘)的=方0 程为 𝑚𝑚 =−2𝑘𝑘 ,𝑚𝑚直=线− 3 𝑘𝑘过定点 ,与已知矛盾,
当𝑚𝑚 =−2𝑘𝑘 时,直线𝐸𝐸𝐹𝐹 的方程为𝑦𝑦=𝑘𝑘(𝑥𝑥−2) ,直线𝐸𝐸𝐹𝐹 过定点(2,0) ;
10 10 10
当𝑚𝑚直线=− 3的𝑘𝑘斜率不存在𝐸𝐸𝐹𝐹时,由对称𝑦𝑦性=不𝑘𝑘妨(𝑥𝑥设−直3线) 的方𝐸𝐸𝐹𝐹程为: 𝑀𝑀(3 ,0),
由 𝐸𝐸𝐹𝐹 解得x=2或 ,因此点 的𝐷𝐷横𝐸𝐸坐标 有𝑦𝑦=𝑥𝑥−2 ,即直线
𝑦𝑦 =𝑥𝑥−2 10 10
� 2 2 𝑥𝑥 = 3 𝐸𝐸,𝐹𝐹 𝑥𝑥𝐸𝐸,𝑥𝑥𝐹𝐹 𝑥𝑥𝐸𝐸 =𝑥𝑥𝐹𝐹 = 3 𝐸𝐸𝐹𝐹
过定𝑥𝑥点−4𝑦𝑦 =4,
10
𝑀𝑀(3 ,0)
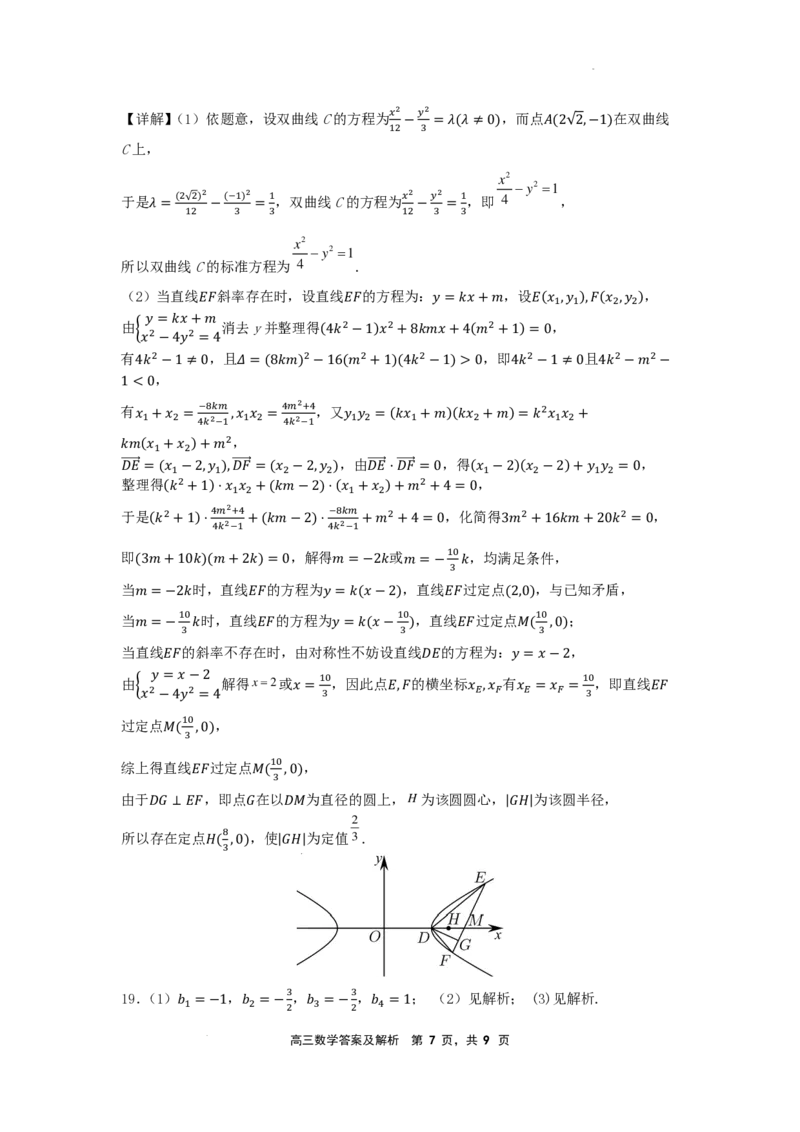
综上得直线 过定点 ,
10
由于 𝐸𝐸𝐹𝐹,即点 𝑀𝑀在(以3 ,0)为直径的圆上,H为该圆圆心, 为该圆半径,
2
𝐷𝐷𝐷𝐷 ⊥𝐸𝐸𝐹𝐹 𝐷𝐷 𝐷𝐷𝑀𝑀 |𝐷𝐷𝐺𝐺|
所以存在定点 ,使 为定值3.
8
𝐺𝐺(3,0) |𝐷𝐷𝐺𝐺|
19.(1) , , , ; (2)见解析; (3)见解析.
3 3
𝑏𝑏1 =−1 𝑏𝑏2 =−2 𝑏𝑏3 =−2 𝑏𝑏4 =1
高三数学答案及解析 第 7 页,共 9 页
学科网(北京)股份有限公司【详解】(1)因为 ,所以 , , ,
𝑛𝑛
所以 , 𝑎𝑎𝑛𝑛 =,2 −3𝑛𝑛 , 𝑎𝑎1 = −1 𝑎𝑎2 =−2 𝑎𝑎3 =−1 𝑎𝑎4 =4
3 3
(2)𝑏𝑏(1必=要−1性)𝑏𝑏当2 =数−列2 𝑏𝑏3是=等−差2数𝑏𝑏列4时=,1 设其公差为d
当 时, ,所以 ,所以 , ,
{𝑎𝑎𝑛𝑛}
当 , ,所以 ,所以 ,
𝑑𝑑 >0 𝑎𝑎𝑛𝑛−𝑎𝑎𝑛𝑛−1 =𝑑𝑑 >0 𝑎𝑎𝑛𝑛 >𝑎𝑎𝑛𝑛−1 𝑀𝑀𝑛𝑛 =𝑎𝑎𝑛𝑛 𝑚𝑚𝑛𝑛 =𝑎𝑎1
当 是, ,所以 ,所以 ,
𝑑𝑑 <0 𝑎𝑎𝑛𝑛−𝑎𝑎𝑛𝑛−1 =𝑑𝑑 <0 𝑎𝑎𝑛𝑛 <𝑎𝑎𝑛𝑛−1 𝑀𝑀𝑛𝑛 =𝑎𝑎1 𝑚𝑚𝑛𝑛 =𝑎𝑎𝑛𝑛
综上𝑑𝑑 =,0总有 𝑎𝑎𝑛𝑛−𝑎𝑎𝑛𝑛−1 =𝑑𝑑 =0 𝑎𝑎𝑛𝑛 =𝑎𝑎𝑛𝑛−1 𝑀𝑀𝑛𝑛 =𝑎𝑎1 𝑚𝑚𝑛𝑛 =𝑎𝑎𝑛𝑛
𝑎𝑎𝑛𝑛+𝑎𝑎1
𝑏𝑏𝑛𝑛 = 2
所以 ,所以数列 是等差数列
𝑎𝑎𝑛𝑛+𝑎𝑎1 𝑎𝑎𝑛𝑛−1+𝑎𝑎1 𝑑𝑑
(充分𝑏𝑏性𝑛𝑛−)𝑏𝑏当𝑛𝑛−数1 =列 2 是−等差2数列=时2,设其公差为{𝑏𝑏𝑛𝑛}
∗
因为 {𝑏𝑏𝑛𝑛} 𝑑𝑑 ,
𝑀𝑀𝑛𝑛+𝑚𝑚𝑛𝑛 𝑀𝑀𝑛𝑛−1−𝑚𝑚𝑛𝑛−1 𝑀𝑀𝑛𝑛−𝑀𝑀𝑛𝑛−1 𝑚𝑚𝑛𝑛−𝑚𝑚𝑛𝑛−1
∗
根据𝑏𝑏𝑛𝑛−,𝑏𝑏𝑛𝑛−的1 =定义2,有−以下结2论: = 2 + 2 =𝑑𝑑
, ,且两个不等式中至少有个取等号
𝑀𝑀𝑛𝑛 𝑚𝑚𝑛𝑛
当 ,则必有 ,所以 ,
𝑀𝑀𝑛𝑛 ≥𝑀𝑀𝑛𝑛−1 𝑚𝑚𝑛𝑛 ≤𝑚𝑚𝑛𝑛−1
所以∗ 是一个单调递增数列,所以 , ,
𝑑𝑑 >0 𝑀𝑀𝑛𝑛 >𝑀𝑀𝑛𝑛−1 𝑎𝑎𝑛𝑛 =𝑀𝑀𝑛𝑛 ≥𝑀𝑀𝑛𝑛−1 ≥𝑎𝑎𝑛𝑛−1
所以{𝑎𝑎𝑛𝑛} 𝑀𝑀𝑛𝑛 =𝑎𝑎𝑛𝑛 𝑚𝑚𝑛𝑛 =𝑎𝑎1
𝑎𝑎𝑛𝑛+𝑎𝑎1 𝑎𝑎𝑛𝑛−1+𝑎𝑎1 𝑎𝑎𝑛𝑛−𝑎𝑎𝑛𝑛−1
∗
所以𝑏𝑏𝑛𝑛−𝑏𝑏𝑛𝑛−1 = 2 ,−即 2 为等=差数2列 =𝑑𝑑
当 时,则必有∗ ,所以
𝑎𝑎𝑛𝑛−𝑎𝑎𝑛𝑛−1 =2𝑑𝑑 {𝑎𝑎𝑛𝑛}
所以∗ 是一个单调递减数列,所以 , ,
𝑑𝑑 <0 𝑚𝑚𝑛𝑛 <𝑚𝑚𝑛𝑛−1 𝑎𝑎𝑛𝑛 =𝑚𝑚𝑛𝑛 <𝑚𝑚𝑛𝑛−1 ≤𝑎𝑎𝑛𝑛−1
所以{𝑎𝑎𝑛𝑛} 𝑀𝑀𝑛𝑛 =𝑎𝑎1 𝑚𝑚 𝑛𝑛 =𝑎𝑎𝑛𝑛
𝑎𝑎𝑛𝑛+𝑎𝑎1 𝑎𝑎1+𝑎𝑎𝑛𝑛−1 𝑎𝑎𝑛𝑛−𝑎𝑎𝑛𝑛−1
∗
所以𝑏𝑏𝑛𝑛−𝑏𝑏𝑛𝑛−1 = 2 ,−即 2 为等=差数2列 =𝑑𝑑
∗
当 𝑎𝑎𝑛𝑛−,𝑎𝑎𝑛𝑛−1 =2𝑑𝑑 {𝑎𝑎𝑛𝑛}
∗
𝑀𝑀𝑛𝑛+𝑚𝑚𝑛𝑛 𝑀𝑀𝑛𝑛−1−𝑚𝑚𝑛𝑛−1 𝑀𝑀𝑛𝑛−𝑀𝑀𝑛𝑛−1 𝑚𝑚𝑛𝑛−𝑚𝑚𝑛𝑛−1
因为𝑑𝑑 =0 𝑏𝑏𝑛𝑛−,𝑏𝑏𝑛𝑛−1 = 2 中−必有一2个为=0, 2 + 2 =0
根据上式,一个为0,则另一个亦为0,
𝑀𝑀𝑛𝑛−𝑀𝑀𝑛𝑛−1 𝑚𝑚𝑛𝑛−𝑚𝑚𝑛𝑛−1
所以 , ,所以 为常数数列,所以 为等差数列
综上,结论得证.
𝑀𝑀𝑛𝑛 =𝑀𝑀𝑛𝑛−1 𝑚𝑚𝑛𝑛 =𝑚𝑚𝑛𝑛−1 {𝑎𝑎𝑛𝑛} {𝑎𝑎𝑛𝑛}
(3)假设结论不成立.
因为 ,即 或者 ,
所以对任意 ,一定存在 ,使得 , 符号相反
|𝑏𝑏𝑛𝑛|=1 𝑏𝑏𝑛𝑛 =1 𝑏𝑏𝑛𝑛 =−1
所以在数列 中∗存在 , , ,……, , ……,其中
𝐾𝐾 ∈𝑁𝑁 𝑠𝑠 >𝐾𝐾 𝑏𝑏𝑖𝑖 𝑏𝑏𝑖𝑖+1
{𝑏𝑏𝑛𝑛} 𝑏𝑏𝑘𝑘1 𝑏𝑏𝑘𝑘2 𝑏𝑏𝑘𝑘3 𝑏𝑏𝑘𝑘𝑖𝑖 𝑏𝑏𝑘𝑘𝑖𝑖+1 𝑘𝑘1 <𝑘𝑘2 <𝑘𝑘3⋯ <𝑘𝑘𝑖𝑖 <
且 ,
⋯
,
−1=𝑏𝑏𝑘𝑘1 =𝑏𝑏𝑘𝑘2 =𝑏𝑏𝑘𝑘3 =⋯=𝑏𝑏𝑘𝑘𝑖𝑖 =𝑏𝑏𝑘𝑘𝑖𝑖+1⋯
1因=为𝑏𝑏𝑘𝑘1+1 =𝑏𝑏𝑘𝑘2+1 =𝑏𝑏𝑘𝑘3,+1即=⋯=𝑏𝑏𝑘𝑘𝑖𝑖+1 =,𝑏𝑏𝑘𝑘𝑖𝑖+1+1⋯
𝑀𝑀𝑘𝑘𝑖𝑖+𝑚𝑚𝑘𝑘𝑖𝑖 𝑀𝑀𝑘𝑘𝑖𝑖+1+𝑚𝑚𝑘𝑘𝑖𝑖+1
注意𝑏𝑏𝑘𝑘𝑖𝑖 =−1,𝑏𝑏𝑘𝑘1,+1 =1 ,2 且有=且−1仅有一个2等号成=立1,
所以必有 ,
𝑀𝑀𝑘𝑘𝑖𝑖+1 ≥𝑀𝑀𝑘𝑘𝑖𝑖 𝑚𝑚𝑘𝑘𝑖𝑖+1 ≤𝑚𝑚𝑘𝑘𝑖𝑖
所以 ,所以
𝑀𝑀𝑘𝑘𝑖𝑖+1 >𝑀𝑀𝑘𝑘𝑖𝑖 𝑚𝑚𝑘𝑘𝑖𝑖+1 =𝑚𝑚𝑘𝑘𝑖𝑖
𝑀𝑀𝑘𝑘𝑖𝑖+1 =𝑀𝑀𝑘𝑘𝑖𝑖+4 高𝑎𝑎𝑘𝑘三𝑖𝑖+数1 =学答𝑀𝑀案𝑘𝑘𝑖𝑖+及1解=析𝑀𝑀 𝑘𝑘 𝑖𝑖第+ 84 页,共 9 页
学科网(北京)股份有限公司因为 ,所以 ,所以
所以
𝑘𝑘𝑖𝑖 >𝑘𝑘𝑖𝑖−1 𝑘𝑘𝑖𝑖 ≥𝑘𝑘𝑖𝑖−1+1 𝑀𝑀𝑘𝑘𝑖𝑖 ≥𝑀𝑀𝑘𝑘𝑖𝑖+1
所以
𝑎𝑎𝑘𝑘𝑖𝑖+1 ≥𝑎𝑎𝑘𝑘𝑖𝑖−1+1+4
所以
𝑎𝑎𝑘𝑘𝑖𝑖+1−𝑎𝑎𝑘𝑘𝑖𝑖−1+1 ≥4
𝑎𝑎𝑘𝑘2+1−𝑎𝑎𝑘𝑘1+1 ≥4
𝑎𝑎𝑘𝑘3+1−𝑎𝑎𝑘𝑘2+1 ≥4
……
𝑎𝑎𝑘𝑘4+1−𝑎𝑎𝑘𝑘3+1 ≥4
所以
𝑎𝑎𝑘𝑘𝑚𝑚+1−𝑎𝑎𝑘𝑘𝑚𝑚−1+1 ≥4
所以
𝑎𝑎𝑘𝑘𝑚𝑚+1−𝑎𝑎𝑘𝑘1+1 ≥4(𝑚𝑚−1)
所以 ,
𝑎𝑎𝑘𝑘𝑚𝑚+1 ≥𝑎𝑎𝑘𝑘1+1+4(𝑚𝑚−1)
这与 矛盾,所以假设错误,
𝑎𝑎𝑘𝑘1010+1 ≥𝑎𝑎𝑘𝑘1+1+4(1010−1)>−2018+4036=2018
所以存在 ,使得,有 .
|𝑎𝑎𝑛𝑛|<2018
∗
𝐾𝐾 ∈𝑁𝑁 𝑏𝑏𝑛𝑛+1 =𝑏𝑏𝑛𝑛
注:具体评分变更信息(分值、答案等)请阅卷教师关注阅卷群。
高三数学答案及解析 第 9 页,共 9 页
学科网(北京)股份有限公司