数学答案（简易版）_8月_240812湖北省腾云联盟2024-2025学年高三上学期8月联考_2-数学

湖北省“腾·云”联盟 2024-2025 学年度上学期 8 月联考 高三数学参考答案 一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有 一项是符合题目要求的. 题号 1 2 3 4 5 6 7 8 答案 B A D A C B A C 二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题 目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分. 题号 9 10 11 答案 AD ACD BCD 三、填空题：本题共3小题，每小题5分，共15分. 1 1 3 12. 3 13. 14. （2分） （3分） 2 2 3 四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤. 15.（13分）【详解】 (1)由题设及正弦定理得，sinBcosC 3sinBsinCsinAsinC 0（1分） 即sinBcosC 3sinBsinCsin(BC)sinC 0（2分） sinBcosC 3sinBsinCsinBcosCsinCcosBsinC 0 0C,sinC 0,  1 整理得 3sinBcosB1,即sin(B ) ,（5分） 6 2    0B，B  ，即B .（7分） 6 6 3  1 （2）由B ,S  acsinB 3得ac4,（9分） 3 2 由余弦定理得b2 a2c22accosBa2c2ac（11分） 即a2c2 8 ac2.（13分） 16.（15分）【详解】（1）函数的定义域为R，f'(x)(x1)ex（1分） 令f'(x)0,解得x1.（2分） 当x1时，f'(x)0, f(x)单调递减； 当x1时，f'(x)0, f(x)单调递增（4分） 当x1时，f(x)有极小值f(1)e（5分） 综上所述，f(x)的单调递增区间为(1,)，单调递减区间为(,1) f(x)极小值为e，且无极大值.（6分） （2）令f(x)0,解得x2 当x2时，f(x)0;当x2时，f(x)0. 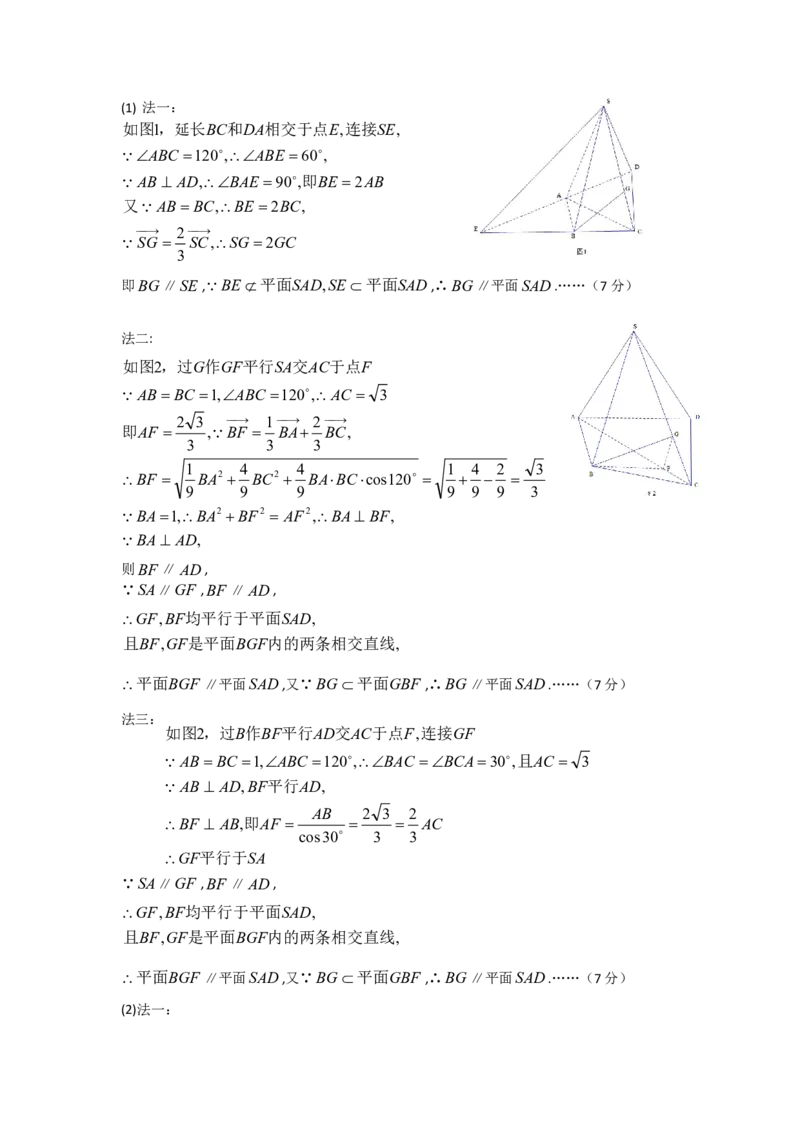x2 当x时，与一次函数相比，指数函数呈爆炸性增长，从而f(x) 0 ex 当x时，f(x) 结合（1）中分析可得，f(x)的大致图象如图所示， …………………………………………………………(8分） 方程 f(x)a的解的个数为函数 y  f(x)的图象与直线 y a的交点个数. 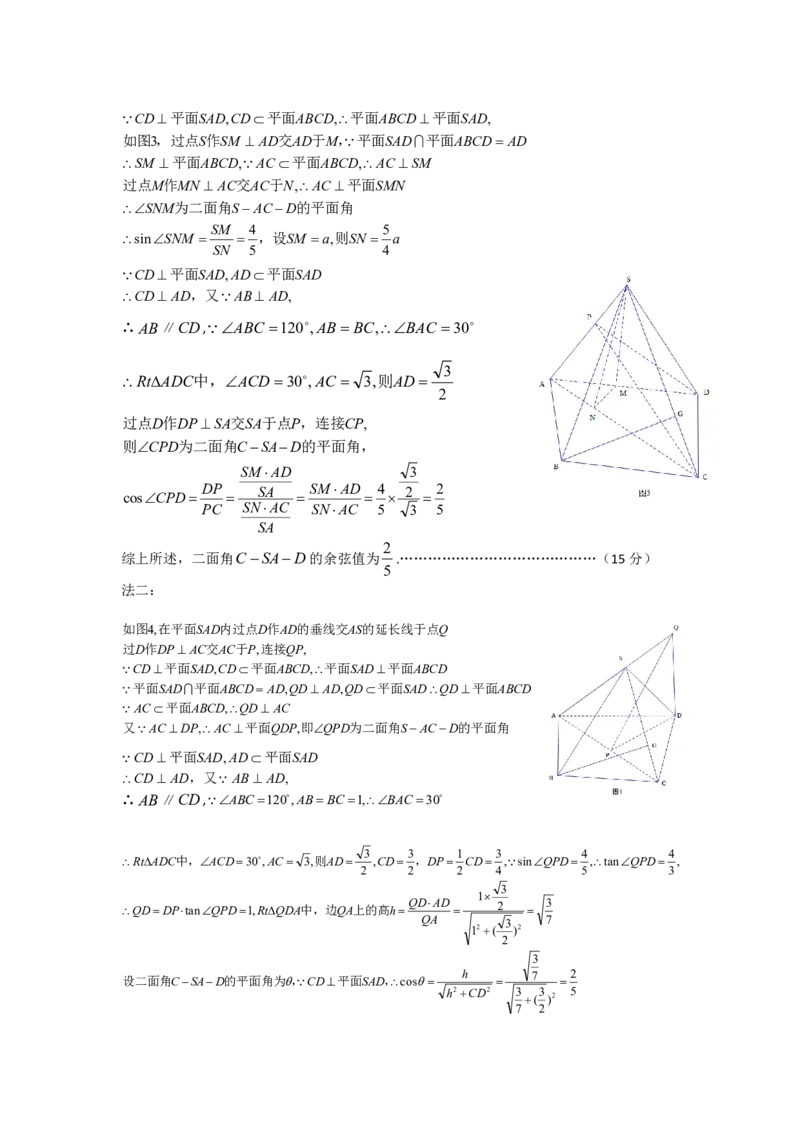由（1）可得当x1时， f(x)有最小值 f(1)e……………………………………(9分） 由图可得，当ae时，方程 f(x)a有0个解…………………………………… (11分） 当a e或a0时，方程 f(x)a有且仅有1个解………………………………（13分） 当ea0时，方程 f(x)a有且仅有两个解……………………………………（15分） 17.（15分）【详解】(1) 法一： 如图1，延长BC和DA相交于点E,连接SE, ABC 120,ABE 60, AB  AD,BAE 90,即BE 2AB 又AB  BC,BE 2BC,  2  SG  SC,SG 2GC 3 即BG∥SE,BE 平面SAD,SE 平面SAD,∴BG ∥平面SAD.……（7分） 法二: 如图2，过G作GF平行SA交AC于点F AB  BC 1,ABC 120,AC  3 2 3  1 2  即AF  ,BF  BA BC, 3 3 3 1 4 4 1 4 2 3 BF  BA2  BC2  BABCcos120     9 9 9 9 9 9 3 BA1,BA2 BF2  AF2,BA BF, BA AD, 则BF ∥AD, ∵SA∥GF ,BF ∥AD, GF,BF均平行于平面SAD, 且BF,GF是平面BGF内的两条相交直线, 平面BGF ∥平面SAD,又∵BG 平面GBF ,∴BG ∥平面SAD.……（7分） 法三： 如图2，过B作BF平行AD交AC于点F,连接GF AB  BC 1,ABC 120,BAC BCA30,且AC  3 AB  AD,BF平行AD, AB 2 3 2 BF  AB,即AF    AC cos30 3 3 GF平行于SA ∵SA∥GF ,BF ∥AD, GF,BF均平行于平面SAD, 且BF,GF是平面BGF内的两条相交直线, 平面BGF ∥平面SAD,又∵BG 平面GBF ,∴BG ∥平面SAD.……（7分） (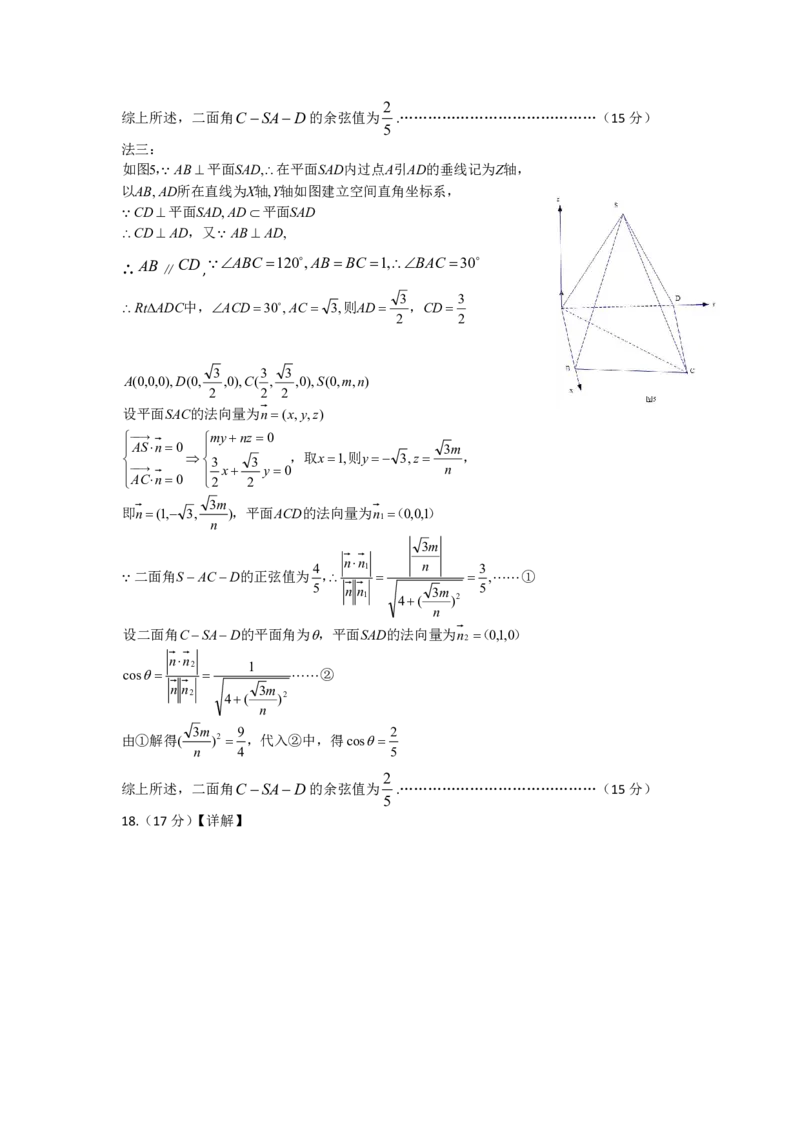2)法一：CD平面SAD,CD平面ABCD,平面ABCD平面SAD, 如图3，过点S作SM  AD交AD于M，平面SAD平面ABCD AD SM 平面ABCD,AC平面ABCD,ACSM 过点M作MN  AC交AC于N,AC平面SMN SNM为二面角SACD的平面角 SM 4 5 sinSNM   ，设SM a,则SN  a SN 5 4 CD平面SAD,AD平面SAD CD AD，又AB AD, ∴AB∥CD,ABC 120,AB  BC,BAC 30 3 RtADC中，ACD 30,AC  3,则AD  2 过点D作DPSA交SA于点P，连接CP, 则CPD为二面角CSAD的平面角， SMAD 3 DP SA SMAD 4 2 2 cosCPD      PC SNAC SNAC 5 3 5 SA 2 综上所述，二面角CSAD的余弦值为 .……………………………………（15分） 5 法二： 如图4,在平面SAD内过点D作AD的垂线交AS的延长线于点Q 过D作DPAC交AC于P,连接QP, CD平面SAD,CD平面ABCD,平面SAD平面ABCD 平面SAD平面ABCDAD,QDAD,QD平面SADQD平面ABCD AC平面ABCD,QDAC 又ACDP,AC平面QDP,即QPD为二面角SACD的平面角 CD平面SAD,AD平面SAD CD AD，又AB AD, ∴AB∥CD,ABC120,ABBC1,BAC30 3 3 1 3 4 4 RtADC中，ACD30,AC 3,则AD ,CD ，DP CD ,sinQPD ,tanQPD , 2 2 2 4 5 3 3 1 QDDPtanQPD1,RtQDA中，边QA上的高h QDAD  2  3 QA 3 7 12( )2 2 3 设二面角CSAD的平面角为，CD平面SAD，cos h  7  2 h2CD2 3 3 5 ( )2 7 22 综上所述，二面角CSAD的余弦值为 .……………………………………（15分） 5 法三： 如图5，AB平面SAD,在平面SAD内过点A引AD的垂线记为Z轴， 以AB,AD所在直线为X轴,Y轴如图建立空间直角坐标系， CD平面SAD,AD平面SAD CD AD，又AB AD, ∴AB∥CD , ABC120,ABBC 1,BAC30 3 3 RtADC中，ACD30,AC 3,则AD ，CD 2 2 3 3 3 A(0,0,0),D(0, ,0),C( , ,0),S(0,m,n) 2 2 2 设平面SAC的法向量为n(x,y,z)  mynz0 ASn0  3m  3 3 ，取x1,则y 3,z ，   x y0 n ACn0 2 2 3m 即n(1, 3, )，平面ACD的法向量为n （0,0,1） 1 n 3m 4 nn 1 n 3 二面角SACD的正弦值为 ，   ,① 5 n n 3m 5 1 4( )2 n 设二面角CSAD的平面角为，平面SAD的法向量为n （0,1,0） 2 nn 2 1 cos  ② n n 3m 2 4( )2 n 3m 9 2 由①解得( )2  ，代入②中，得cos n 4 5 2 综上所述，二面角CSAD的余弦值为 .……………………………………（15分） 5 18.（17分）【详解】（1）依题意可得QC Q AQC QP 4,C A24，(1分) 1 1 1 1 1 1 1 1 x2 y2 点Q的轨迹是以C ,A为焦点，4为长轴长的椭圆,即 :  1(3分) 1 1 1 4 3 依题意可得Q C Q A  Q C Q P 1,C A21，(4分) 2 2 2 2 2 2 2 2 x2 y2 点Q的轨迹是以C ,A为焦点，1为实轴长的双曲线,即 :  1(6分) 2 2 2 1 3 4 4 （2）设M(x ,y ),N(x ,y ) 1 1 2 2 x2 y2   1 4k 联立 4 3 消去y得，(34k2)x28kx80，由韦达定理可得x  ，(8分)  1 34k2 ykx1 x2 y2   1  1 3 7 k 联立 消去y得，(3k2)x22kx 0，由韦达定理可得x  ，(10分)  4 4 4 2 3k2  ykx1 4k k 则线段MN的长度为 1k2 x x  1k2  (11分) 1 2 34k2 3k2 1 点O到直线l的距离为 ，(12分) 1k2 1 1 4k k 1 15k 15 S    1k2     ，(13分) MON 2 1k2 34k2 3k2 2 (34k2)(3k2) 28 k 1 即  ， (34k2)(3k2) 14 0k  3,(34k2)(3k2)14k， 4k49k214k90, 法一：4k44(9k214k5)0   4(k21)(k21)(9k5)(k1)0,(k1)4(k1)(k21)9k5 0, 方程有一解为k 1(15分) 令f(k)4k34k25k9, f'(k)12k28k5在（0，3）上单调递增， f'(0)50, f'(1)150, k (0,1),使得f '(k )0, f(k)在（0，k）上单调递减，    在（k ,1）上单调递增，即当k(0, 3)时，  f(k)  f(k )4k 34k 2 5k 94k 34k 2 5940 min        f(k)0在（0，3）上无解. 综上所述，直线l的斜率k的值为1.（17分）法二：设f(k)4k4 9k2 14k9，显然f(1)0 f '(k)16k3 18k142(8k3 9k7), 令g(k)8k3 9k7,g'(k)24k2 9, 6 当g'(k)0时,k  , 4 6 当k(0, )时，g'(k)0,g(k)单调递减， 4 6 当k( ，3)时，g'(k)0,g(k)单调递增， 4 6 当k(0, 3)时，g(k)  g( )72 6 0 min 4 g(k)0在(0, 3)上恒成立，即f(k)在(0, 3)单调递增， g(k)0在(0, 3)上有且仅有一解， 综上所述，直线l的斜率k的值为1.（17分） 19．（17分） 【详解】（1）将数列1,2进行第一次“A型拓展”得到1,2,2；进行第二次“A型拓展”得到 1,2,2,4,2；进行第三次“A型拓展”得到1,2,2,4,2,8,4,8,2；所以第6项为8；…………（3分） （2） 当a 1,b2时，a log（1x x x 2） n 2 1 2 t   a log 1(1x )x (x x )x (x x )(x x )x (x 2)2 n1 2 1 1 1 2 2 2 3 t1 t t t   log（12x3x 3 x322）log（13x3x 3 x323）2 3a 1 2 1 2 t 2 1 2 t n 1 1 1 1 3 所以a  3(a  ),又a  log (122)  n1 2 n 2 1 2 2 2 2  1 3 1 3 3n 从而 a   是首项为 ，公比为3的等比数列，a   3n1   n 2 2 n 2 2 2 3n 1 a  （7分） n 2 b log（1y y y 2） n 2 1 2 t  y y y y 2  b log 1( 1)y ( 2)y ( 3)y ( t )y ( )2 n1 2  1 1 y 2 y 3 y t y  1 2 t1 t log (y y y 22)log (y y y 2)2b 1 2 1 2 t 2 1 2 t n 2 b b 1,b log (1 2)2 n1 n 1 2 1 即 b 是以2为首项，1为公差的等差数列，b 2(n1)1n1.（11分） n n（3） 将数列 c 进行B型拓展后得到数列 d  k m 显然，S T d d d d 2 4 6 2n c c c c c d  2 ,d  3 ,d  4 ,,d  k1,,d  n1 2 c 4 c 6 c 2k c 2n c 1 2 3 k n 3n 1 3n 1 a 1 1 n 2 2 3n 1 3n11 且  3n1, 2 2   a 1可以看作是数列 3n1的前n项和， n 即1,3,32,33，，3n1分别对应d ,d ,d ,d 2 4 6 2n c 取c 1, k1 d 3k1 1 c 2k k c c c c c 当k 2时，c  k  k1  k2  3  2 c 3k23k33k4311 k c c c c c 1 k1 k2 k3 2 1 (k1)(k2) 3 2 1,k 1  即c k  (k1)(k2) （17分）  3 2 ,2k n1,kN