文档内容
2023—2024 年度高二年级下学期期末考试模拟卷
数学参考答案
1.D ∵A={x|0≤x≤2},∴ A={x|x<0或x>2}.∵B={x|x>0},∴( A)∩B={x|x>2}.
∁U ∁U
(i-1)2 -2i -2i(1-i)
2.B = = =-1-i.
1+i 1+i 2
2
3.B 因为a2=4,b2=9,所以a=2,b=3,所以该双曲线的渐近线方程为y=± x,即2x±3y=0.
3
a (1-q3)
4.C 因为S
2
=3a
2
,所以a
1
=2a
2
,所以公比q=1,所以 S 3= 1
1-q
= 1-q3 =7.
2 a q2(1-q)
3 a q2
1
a a-x
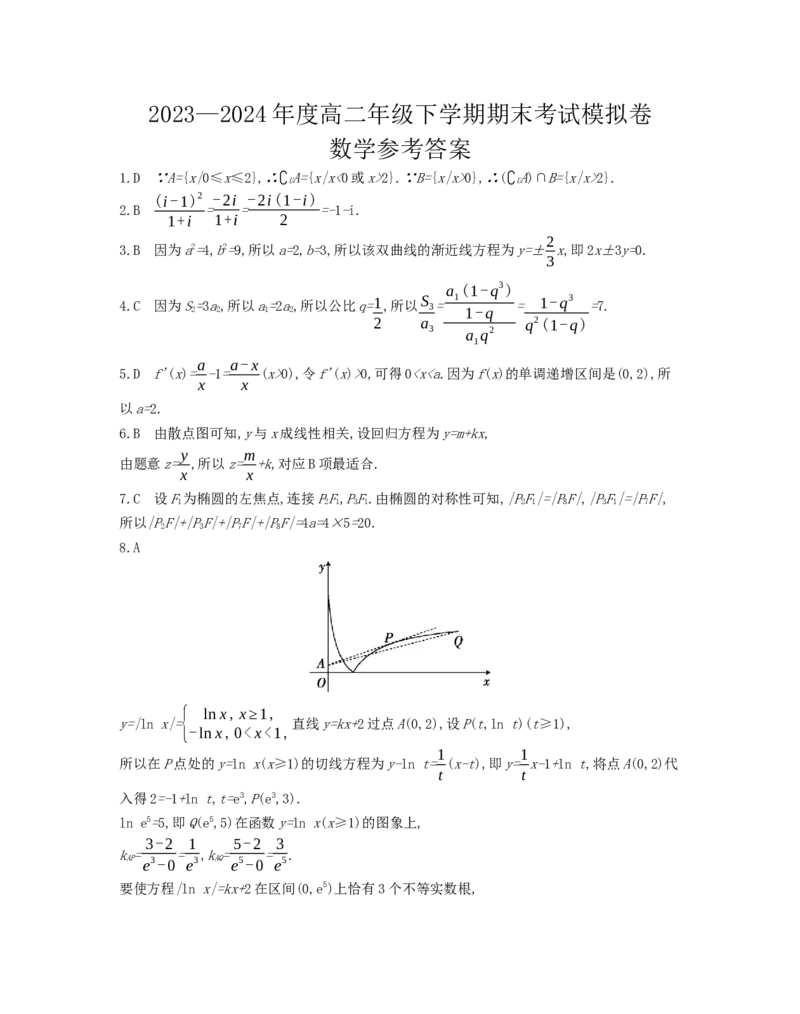
5.D f'(x)= -1= (x>0),令f'(x)>0,可得03.841,所以由参考数据
30×75×55×50
知能在犯错误的概率不超过0.05的前提下认为药物有效,故A项正确;又6.1>5.024,所以由参
考数据知能在犯错误的概率不超过0.025的前提下认为药物有效,故B项错误;又6.1<6.635,
所以由参考数据知不能在犯错误的概率不超过0.010的前提下认为药物有效,故C项错误;又
6.1<7.879,所以由参考数据知不能在犯错误的概率不超过0.005的前提下认为药物有效,故D
项正确.
1 1 5
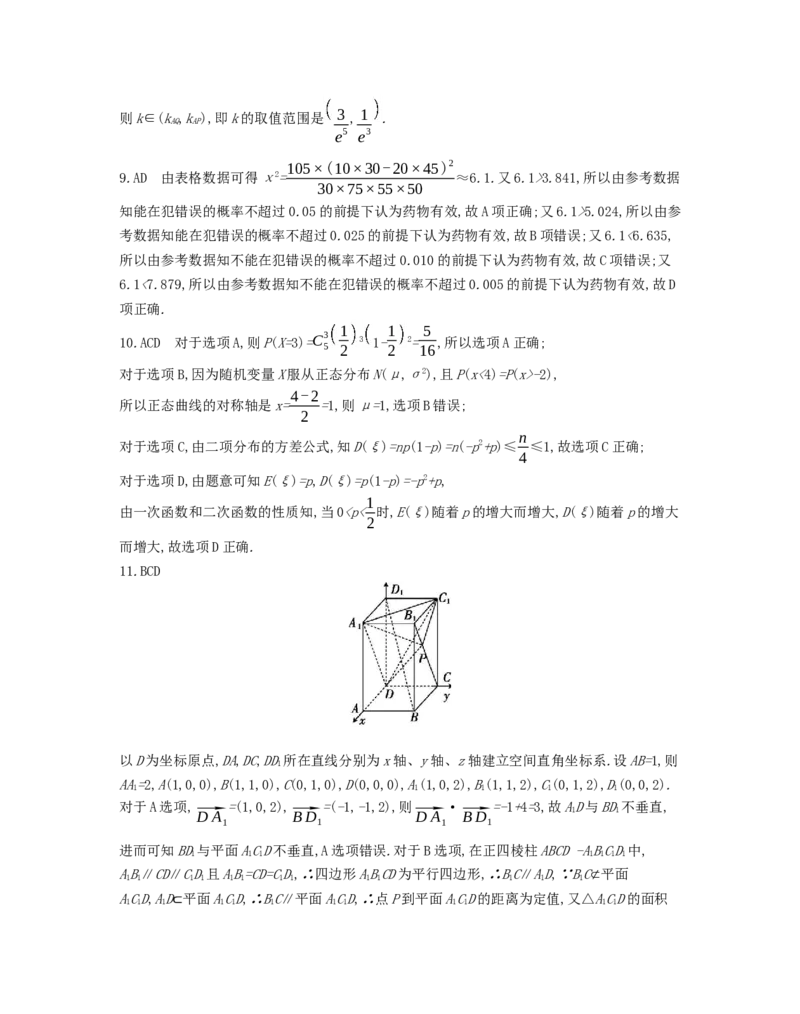
10.ACD
对于选项A,则P(X=3)=C3
3 1- 2= ,所以选项A正确;
5 2 2 16
对于选项B,因为随机变量X服从正态分布N(μ,σ2),且P(x<4)=P(x>-2),
4-2
所以正态曲线的对称轴是x= =1,则μ=1,选项B错误;
2
n
对于选项C,由二项分布的方差公式,知D(ξ)=np(1-p)=n(-p2+p)≤ ≤1,故选项C正确;
4
对于选项D,由题意可知E(ξ)=p,D(ξ)=p(1-p)=-p2+p,
1
由一次函数和二次函数的性质知,当03.841,
100×100×150×50 3
所以有95%的把握认为对兴趣小组的满意度与初、高中学生有关.
150 50
(2)满意的中学生抽取8× =6(人),不满意的学生中抽取8× =2(人),
200 200
依题意,X的可能取值为0,1,2,
则P(X=0)= C 6 0C 2 2 =1 ,P(X=1)= C1 6 C1 2=3,P(X=2)= C 6 2C 2 0 =15,
C2 28 C2 7 C2 28
8 8 8
所以X的分布列如下:
X 0 1 2
学科网(北京)股份有限公司1 3 15
P
28 7 28
1 3 15 3
所以E(X)=0× +1× +2× = .
28 7 28 2
16.解:(1)连接BF,∵点C,F是 ⏜ 的两个三等分点,
AB
∴BF∥OC,∴BF∥平面OCD,又CD、BE均为圆柱的母线,∴BE∥CD,
∴BE∥平面OCD,又BE∩BF=B,∴平面BEF∥平面OCD,
又EF 平面BEF,∴EF∥平面OCD.
(2)连接BC,∵AB是圆O的直径,∴AC⊥BC,
⊂
又CD为圆柱的母线,故CD,CA,CB两两垂直,
建立如图所示的空间直角坐标系,
由条件得D(0,0,4),A(2,0,0),C(0,0,0),O(1, ,0),E(0,2 ,4),M 1,3√3,2 ,
√3 √3
2 2
=(2,0,0), = 1,3√3,2 ,
⃗CA ⃗CM
2 2
设平面ACM的法向量n=(x,y,z),
1
{ n ·⃗CA=2x=0,
1
则
1 3√3
n ·⃗CM= x+ y+2z=0,
1 2 2
取y=4,得n=(0,4,-3 ),显然平面ACD的一个法向量 n=(0,1,0),
1 2
√3
∴cos= n 1 ·n 2= 4 =4√43,
|n||n | √43 43
1 2
4√43
故所求二面角D -AC -M的余弦值为 .
43
17.解:(1)X的所有取值为0,1,2,由题意知,
学科网(北京)股份有限公司P(X=0)= C2 4 C 2 0 =2,P(X=1)= C1 4 C1 2=8 ,P(X=2)= C0 4 C 2 2 =1 ,
C2 5 C2 15 C2 15
6 6 6
∴X的分布列为
X 0 1 2
2 8 1
Y
5 15 15
2 8 1 2
∴E(X)=0× +1× +2× = .
5 15 15 3
(2)对y=menx(m>0)两边取自然对数,得ln y=ln m+nx,设t=ln y,
6 − −
∑x t -6x t
i i 31.89-6×3.5×1.16
∴t=ln m+nx,∵n=i=1 = ≈0.43,
6 91-6×3.52
∑x2-6x2
i
i=1
−=ln m+n− ln m=−-0.43−=1.16-0.43×3.5≈-0.35,
t x t x
⇒
又e-0.35≈0.7047,∴m≈0.70,∴y=0.70·e0.43x.
{x2 y2
18.解:(1)由方程组 + =1,消去y并整理得4x2+6tx+3t2-12=0.
12 4
x- y+t=0
因为直线l与椭圆没有公共点,所以Δ=36t2-4×4×(3t2-12)<0,
解得t>4或t<-4,所以实数t的取值范围为(-∞,-4)∪(4,+∞).
(2)点P到直线l距离的最大值等价于与直线l平行且与椭圆C相切的直线与直线l间的距离.
由(1)知,直线l:x-y+4=0与直线l:x-y-4=0与椭圆C相切.
1 2
当l与l之间的距离为6 时,得 t-4 =6 ,解得t=-8或t=16(舍去);
1 √2 √2
√2
当l与l之间的距离为6 时,得 t+4 =6 ,解得t=8或t=-16(舍去).
2 √2 √2
√2
综上所述,所求直线l的方程为x-y-8=0或x-y+8=0.
学科网(北京)股份有限公司19.解:(1)f'(x)=(x-a)·ex-1,令f'(x)=0,得x=a或x=0.
ex
当a>0时,由f'(x)>0,得x>a或x<0,由f'(x)<0,得00,得x∈R,
ex
所以f(x)在R上单调递增.
当a<0时,由f'(x)>0,得x0;由f'(x)<0,得a0时,f(x)在(-∞,0)和(a,+∞)上单调递增,在(0,a)上单调递减;当a=0时,
f(x)在R上单调递增;
当a<0时,f(x)在(-∞,a)和(0,+∞)上单调递增,在(a,0)上单调递减.
(2)(i)当a∈(0,1)时,g(x)=f(x)-f(0)=f(x)+a-1,
g(x)与f(x)的单调性相同,
由(1)知,当a∈(0,1)时,g(x)在(0,a)上单调递减,在(a,+∞)上单调递增,
所以g(a)0,
e2a+2
所以函数g(x)在区间(0,+∞)内有唯一的零点.
x 1
(ii)设h(x)=ex- -1,则h'(x)=ex- .
1-a 1-a
由h'(x)>0,得x>-ln(1-a);由h'(x)<0,得00,所以φ(x)在(0,1)上单调递增,
(1-a)2e2a
所以φ(a)>φ(0)=0,所以f(2a)>f(0),得证.
学科网(北京)股份有限公司