江苏省南京市协同体七校2024-2025学年高三上学期期中联合考试数学试题+答案(1)_12月_241201江苏省南京市协同体七校2025届高三期中联合考试（全科）

南京市协同体七校 2024-2025 学年第一学期期中联合考试 高三数学试题 考试时间：120分钟 满分：150分 南京市第 66中学 席青云 南京市文枢高级中学 漆光宗 命制 注意事项： 1.本试卷所有试题必须作答在答题卡上规定的位置，否则不给分. 2.答题务必将自己妵名，准考证信息用 0.5毫米黑色墨水签字笔填写在试卷答题卡上， 第 I 卷（选择题共 58分） 一､选择题：本题共 8小輀，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1.已知集合A={ x∣log x<2 } ,B={ x∣x>2 } ，则A∪B=（ ） 2 A. ( 0,2 ) B. ( 0,+∞) C. ( 2,+∞) D. (−∞,2 ) 2.若2z−1=i，则 z =（ ） 2 1 A. 2 B.1 C. D. 2 2       3.已知向量a =( 0,4 ) ,b =( 3,6 ) ,c =(−1,6 )，若c =λa+µb，则λ+µ=（ ） 7 5 1 2 A. B. C.− D.− 3 3 3 3 1 4 4.已知m>0,n>0，且m+n=1，则 + 的最小值为（ ） m n A.12 B.9 C.6 D.3 5.已知直径为12的球内有一内接圆柱（圆柱上下底面圆在球面上），则圆柱体积的最大值为（ ） A.96 3π B.96π C.48 3π D.192π 6.已知函数 f ( x )=   2x+4,xa, 在R上单调递增，则实数a的取值范围是（ ） x2 +1,x>a A. (−1,3 ] B. (−∞,3 ] C. [ 3,+∞) D. ( −∞,−1 ]∪[ 3,+∞ ) 7.将一枚均匀的骰子掷两次，记事件A为“第一次出现偶数点”，事件B为“两次出现的点数和为9”， 则下列结论中正确的是（ ） 1 A.P ( AB )= B.P ( A∪B )= P ( A )+P ( B ) 9 1 C.P ( A∣B )= D.A与B相互独立 3 学科网（北京）股份有限公司8.已知 f ( x ) 是定义在R上的周期函数，周期T =1，且当x∈[ 0,1 ) 时 f ( x )= x2，若g ( x )=kx+b，则 下列结论中一定正确的是（ ） A.k =1时， f ( x )= g ( x ) 可以有三个解 1 B.k = 时， f ( x )= g ( x ) 可以有三个解 2 C.k =−1时， f ( x )= g ( x ) 可以有一个解 1 D.k =− 时， f ( x )= g ( x ) 可以有四个解 2 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9.已知抛物线C: y2 =4x，直线l: y =kx−k与抛物线C交于P,Q两点，分别过P,Q两点作抛物线准线 的垂线PM,QN，垂足分别是M,N ，下列说法正确的是（ ） A.直线l过抛物线C的焦点 B.当k =1时，P,Q两点横坐标的和为5 C.当k =1时，直线l截抛物线所得的弦长为8 D.以MN为直径的圆与直线l相切    10.已知正方体ABCD−ABC D ，点P满足BP=λBC+µBB,λ∈  0,1 ] ,µ∈[ 0,1  ，则下列说法正确 1 1 1 1 1 的是（ ） A.存在唯一一点P，使得过D,B,P的平面与正方体的截面是菱形 1 B.存在唯一一点P，使得AP⊥平面BDC 1 1 C.存在无穷多个点P，使得AP∥平面ACD 1 D.存在唯一一点P，使得DP⊥ BC 1 1 11.如果X 服从二项分布B ( n,p ) ，当np >10且n ( 1− p )>10时，可以近似的认为X 服从正态分布 ( ) N µ,σ2 ，据统计高中学生的近视率P=0.6，某校有600名高中学生.设X 为该校高中学生近视人数， ( ) 且X 服从正态分布N µ,σ2 ，下列说法正确的是（ ） （参考数据：P(µ−σ< X <µ+σ)≈0.682,P(µ−2σ< X <µ+2σ)≈0.9545） ( ) A.变量X 服从正态分布N 360,144 学科网（北京）股份有限公司B.P ( X372 )≈0.159 C.P(X <384)= P ( X >348 ) D.P(X <384)≈0.9773 第 II 卷（非选择题共 92分） 三､填空题：本题共 3小题，每小题 5分，共 15分. 12.在等差数列 { a } 中，a =2n−1 ( n∈N* ) ，则S =__________. n n 20  π  π 13.已知函数y =2sin ωx−  (ω>0 ) 在区间0, 上有且仅有2个零点，则实数ω的取值范围是  6  2 __________.__________. 14.已知e为自然对数的底数，若函数y =lnx+ax的最大值与函数y =ex −x的最小值相等，则实数a的 值是__________. 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 15.（本题满分13分） c 在ABC中，角A,B,C所对的边长分别为a,b,c，已知b=5,c=3,b=acosC− . 2 （1）求∠A； （2）若D是BC中点，求AD的长度. 16.（本题满分15分） 已知公差不为0的等差数列 { a } 的前n项和为S ,S =35,a ,a ,a 成等比数列. n n 5 1 4 13 { } （1）求 a 的通项公式； n 1 1 1 （2）若mb>0 )的短轴长为2，离心率为 ,A,B分别是椭圆C的上下顶点，过A a2 b2 3 作两条互相垂直的直线AP,AQ，分别交椭圆C于P,Q两点. （1）求椭圆C的标准方程； （2）求证：直线PQ恒过定点； （3）求APQ面积的最大值. 学科网（北京）股份有限公司南京市协同体七校 2024—2025 学年第一学期期中联合考试 高三数学参考答案 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1.B 2.C 3.B 4.B 5.A 6.C 7.D 8.B 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9.ACD 10.BD 11.ABD 三､填空题：本题共 3小题，每小题 5分，共 15分. 7 13 1 12.400 13. ,  14.− 3 3  e2 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 15.（本题满分13分） 解：（1）方法一： c 因为b=acosC− ， 2 1 由正弦定理得：sinB=sinAcosC− sinC， 2 又sinB=sinAcosC+cosAsinC， 1 2π 所以cosA=− ，又因为在ABC中，所以A= . 2 3 方法二： c 因为b=acosC− ,b=5,c=3， 2 a2 +25−9 3 由余弦定理得：5=a − ， 2a×5 2 解得a2 =49， 25+9−49 1 所以cosA= =− ， 2×5×3 2 2π 又因为在ABC中，所以A= . 3 （2）方法一：    1 1 在ABC中，D是BC中点，所以AD= AB+ AC ， 2 2 学科网（北京）股份有限公司    1 2 1 1 2 1 1  1 1 19 | AD|2= AB + ABAC+ AC = ×9+ ×3×5×  −  + ×25= ， 4 2 4 4 2  2 4 4  19 19 AD = ，即AD的长为 . 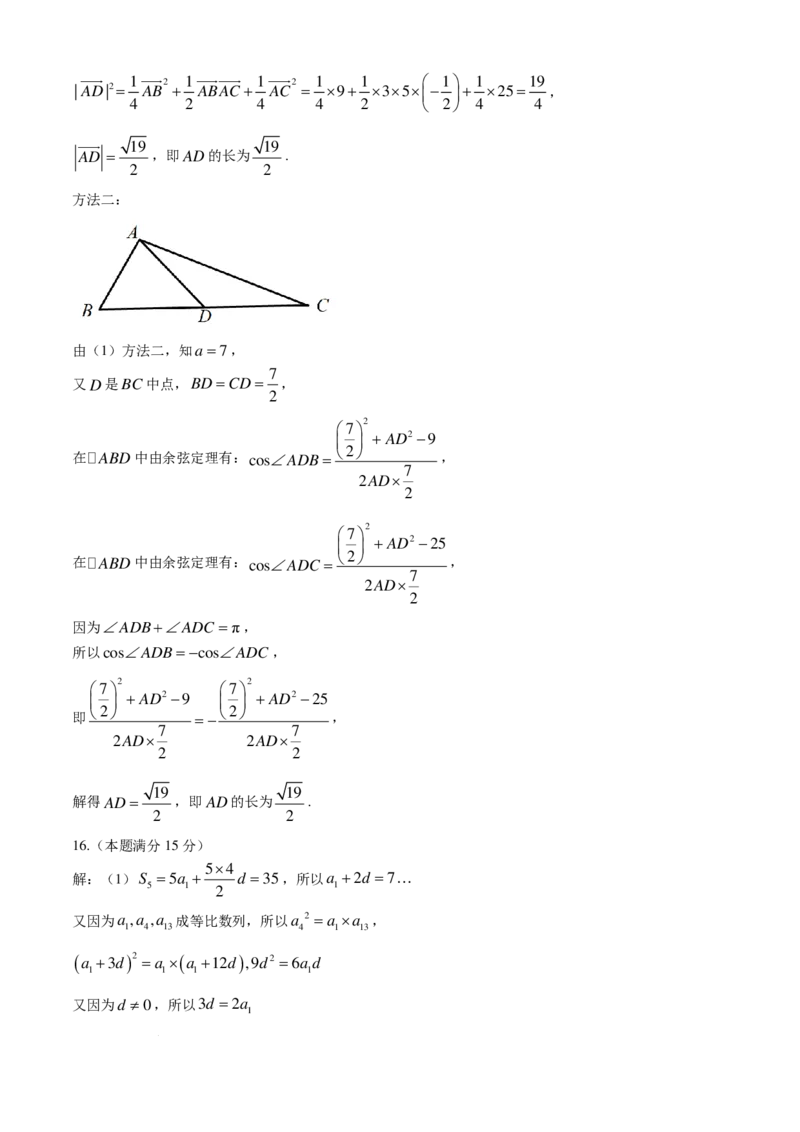2 2 方法二： 由（1）方法二，知a =7， 7 又D是BC中点，BD=CD= ， 2 2 7   + AD2 −9 2 在ABD中由余弦定理有：cos∠ADB= ， 7 2AD× 2 2 7   + AD2 −25 2 在ABD中由余弦定理有：cos∠ADC = ， 7 2AD× 2 因为∠ADB+∠ADC =π， 所以cos∠ADB=−cos∠ADC， 2 2 7 7   + AD2 −9   + AD2 −25 2 2 即 =− ， 7 7 2AD× 2AD× 2 2 19 19 解得AD= ，即AD的长为 . 2 2 16.（本题满分15分） 5×4 解：（1）S =5a + d =35，所以a +2d =7… 5 1 2 1 又因为a ,a ,a 成等比数列，所以a 2 =a ×a ， 1 4 13 4 1 13 ( a +3d )2 =a ×( a +12d ) ,9d2 =6ad 1 1 1 1 又因为d ≠0，所以3d =2a 1 学科网（北京）股份有限公司所以a =3,d =2 1 所以a =2n+1 n 2 1 1 （2）由题意： = + a a a m 1 n 2 1 1 所以 = + 2m+1 3 2n+1 方法一： 2 2n+4 = 2m+1 6n+3 6n+3 9 所以2m+1= =6− ， n+2 n+2 因为m ， 2m+1 3 2n+1 3 5 所以，m< ， 2 又m∈N*，所以m=1或m=2， 当m=1时，n=1，与m0 ) x x x 若a0，则x∈( 0,1 ) 时 f′( x )<0, f ( x ) 单调递减，x∈( 1,+∞) 时 f′( x )>0, f ( x ) 单调递增； 若00, f ( x ) 单调递增，x∈( a,1 ) 时 f′( x )<0, f ( x ) 单调递减， x∈( 1,+∞) 时 f′( x )>0, f ( x ) 单调递增 若a=1，则x∈( 0,+∞) 时 f′( x )>0, f ( x ) 单调递增 若a>1，则x∈( 0,1 ) 时 f′( x )>0, f ( x ) 单调递增，x∈( 1,a ) 时 f′( x )<0, f ( x ) 单调递减，x∈( a,+∞) 时 f′( x )>0, f ( x ) 单调递增 1 （3）令h ( x )= f ( x )+( a+1 ) x= x2 +alnx， 2 a x2 +a h′( x )= x+ = , ( x>0 ) , x x 当a0时，h′( x ) 0，故无最小值 所以a<0，由h′( x )=0得x= −a， ( ) ( ) 所以x∈ 0, −a 时h′( x )<0,h ( x ) 单调递减，x∈ −a,+∞ 时h′( x )>0,h ( x ) 单调递增单增， ( ) 1 所以h(x) =h −a =− a+aln −a =0， min 2 所以ln (−a )=1,a =−e. 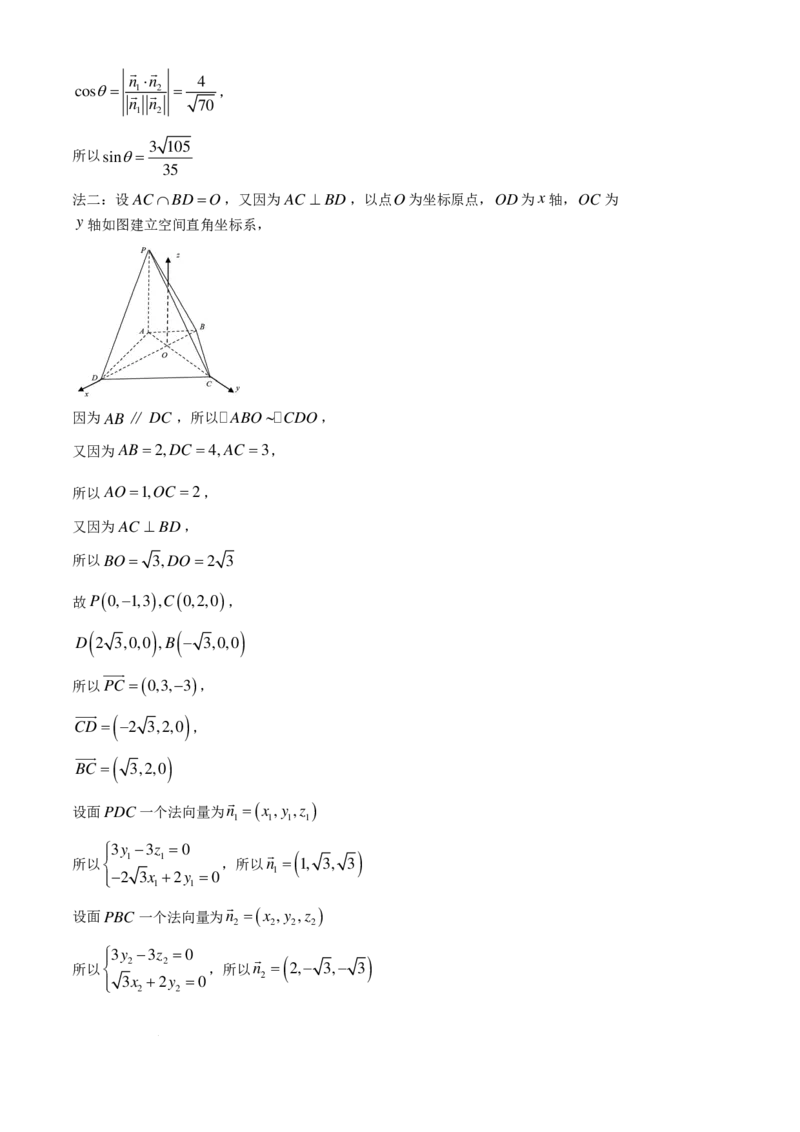19.（本题满分17分） c 2 2 （1）解：因为2b=2, = ，又a2 =b2 +c2 a 3 学科网（北京）股份有限公司解得：a=3,b=,c= 3 x2 故椭圆的标准方程为： + y2 =1 9 （2）证明： 方法一： 当PQ⊥ x轴时，AP,AQ不可能垂直， 故可设直线PQ方程为：y =kx+n y =kx+n  ( ) 由x2 ，得 1+9k2 x2 +18knx+9n2 −9=0，  + y2 =1  9 ( ) ( ) 设P x ,y ,Q x ,y 1 1 2 2 −18kn 9n2 −9 则：x +x = ,x x = ， 1 2 1+9k2 1 2 1+9k2     所以，PA=( x ,y −1 ) ,PQ=( x ,y −1 )，又因为PA⊥ PB，所以PA⋅PQ=0 1 1 2 2 即x x +( y −1 )( y −1 )=0即：x x +( kx +n−1 )( kx +n−1 )=0， 1 2 1 2 1 2 1 2 所以，x x +k2x x +k ( n−1 )( x +x )+(n−1)2 =0 1 2 1 2 1 2 9n2 −9 9n2k2 −9k2 −8n2k2 +18k2n (n−1)2 +9k2(n−1)2 代入可得： + + + =0， 1+9k2 1+9k2 1+9k2 1+9k2 4 整理：10n2 −2n−8=0，所以：n=1（舍）或n=− ， 5 4 4 所以直线PQ的方程为：y =kx− ，令x=0，得y =− ， 5 5  4 所以直线PQ过定点0,− ，  5 方法二： 显然AP,AQ均不可能与坐标轴垂直，故可设AP: y =kx+1 ( k ≠0 ) y =kx+1  ( ) 由x2 ，得 1+9k2 x2 +18kx=0  + y2 =1  9 ( ) ( ) 设P x ,y ,Q x ,y 1 1 2 2 学科网（北京）股份有限公司−18k 1−9k2 所以：x = ,y = ， 1 1+9k2 1 1+9k2 18k k2 −9 因为AP,AQ互相垂直，同理得x = ,y = 2 9+k2 2 9+k2 k2 −1 所以直线PQ的斜率为：k = ， PQ 10k 1−9k2 k2 −1 18k  直线PQ的方程为：y− = x+ ， 1+9k2 10k  1+9k2  ( ) 1−9k2 9 k2 −1 4  4 令x=0得y = + =− ，即直线PQ过定点0,− . 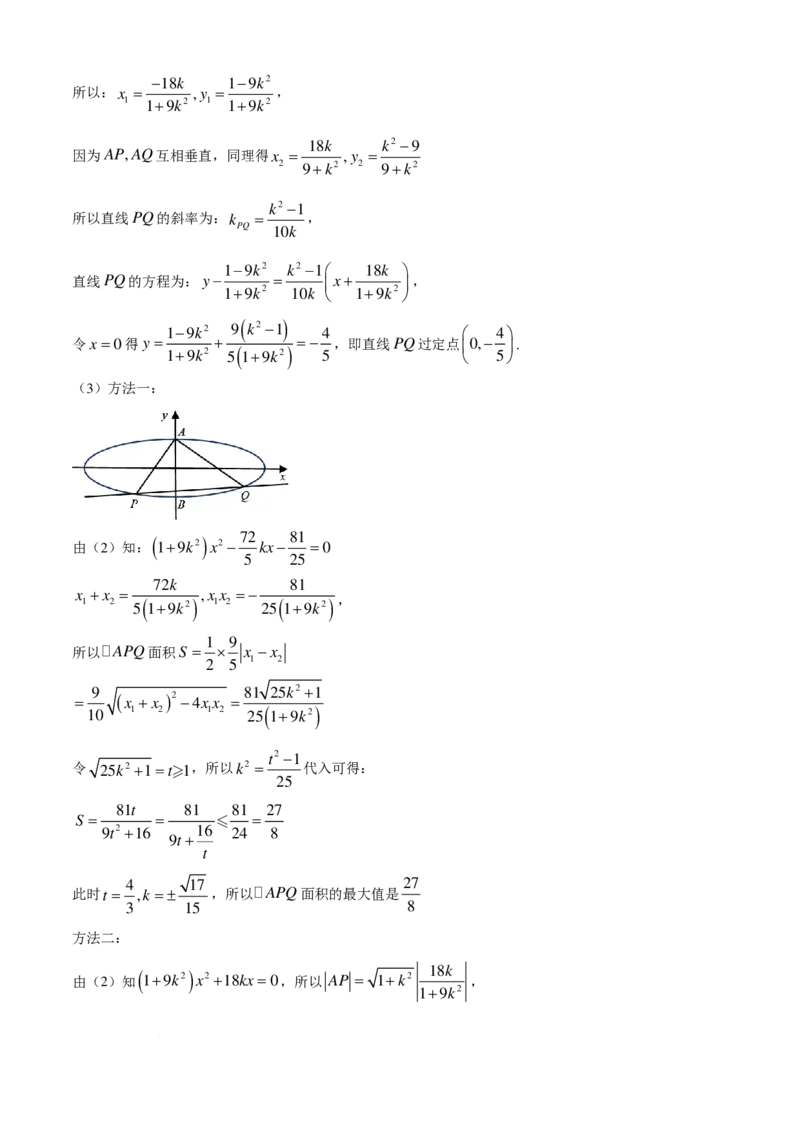1+9k2 5 ( 1+9k2 ) 5  5 （3）方法一： ( ) 72 81 由（2）知： 1+9k2 x2 − kx− =0 5 25 72k 81 x +x = ,x x =− 1 2 5 ( 1+9k2 ) 1 2 25 ( 1+9k2 )， 1 9 所以APQ面积S = × x −x 2 5 1 2 9 81 25k2 +1 = 10 ( x 1 +x 2 )2 −4x 1 x 2 = 25 ( 1+9k2 ) t2 −1 令 25k2 +1=t1，所以k2 = 代入可得： 25 81t 81 81 27 S = =  = 9t2 +16 16 24 8 9t+ t 4 17 27 此时t = ,k =± ，所以APQ面积的最大值是 3 15 8 方法二： ( ) 18k 由（2）知 1+9k2 x2 +18kx=0，所以 AP = 1+k2 ， 1+9k2 学科网（北京）股份有限公司1 18k 因为AP,AQ互相垂直，同理得 AQ = 1+ ， k2 9+k2 1 18k 1 18k 所以APQ面积S = AP AQ = 1+k2 1+ 2 1+9k2 k2 9+k2  1  162 k ( 1+k2 )   k + k     = =162 9k4 +82k2 +9 9 9k2 +82+ k2 1 t 1 162 27 + k =t,S =162× =162×  = 令 k 9t2 +64 64 48 8 ， 9t+ t 8 1 此时t = ，解得k =±3或k =± ， 3 3 27 所以APQ面积的最大值是 . 8 学科网（北京）股份有限公司