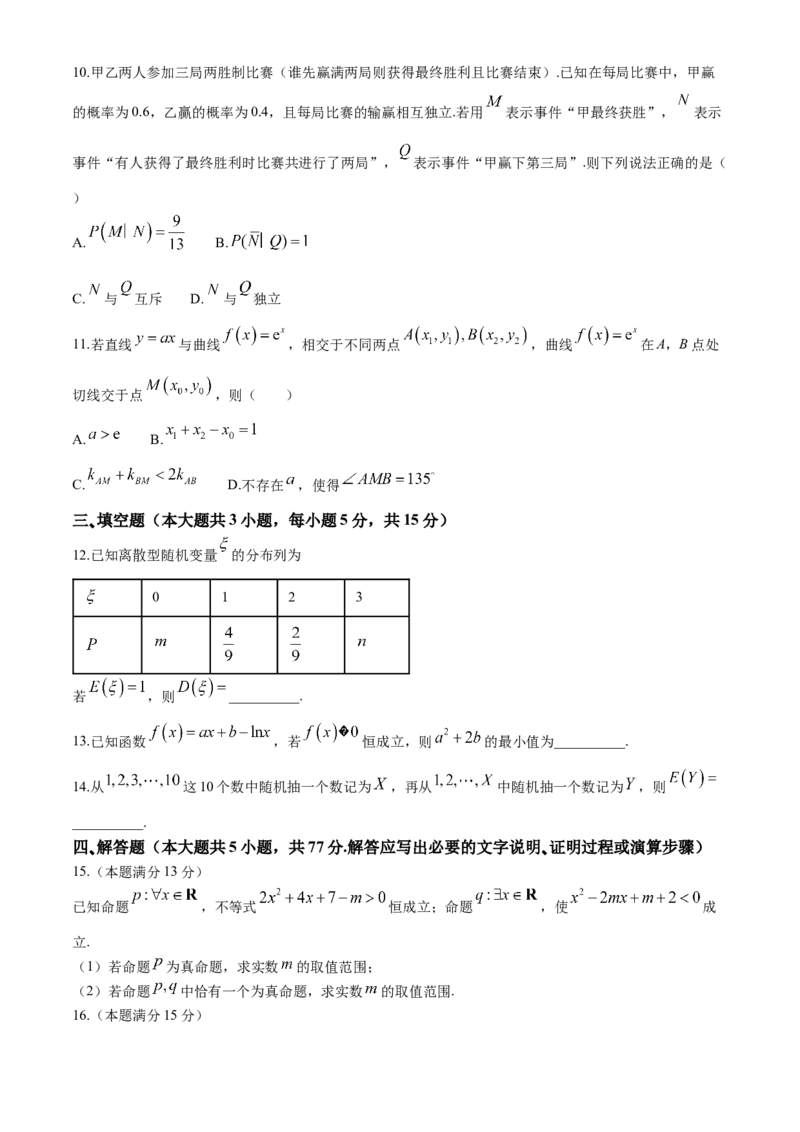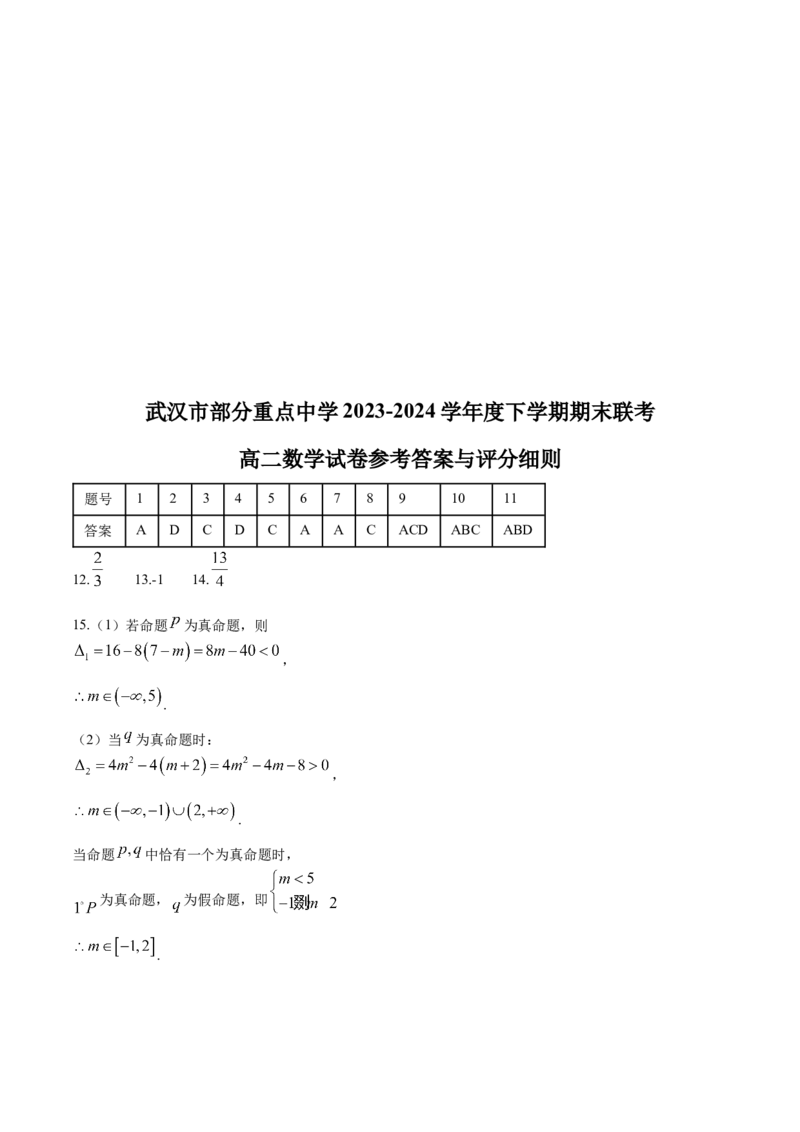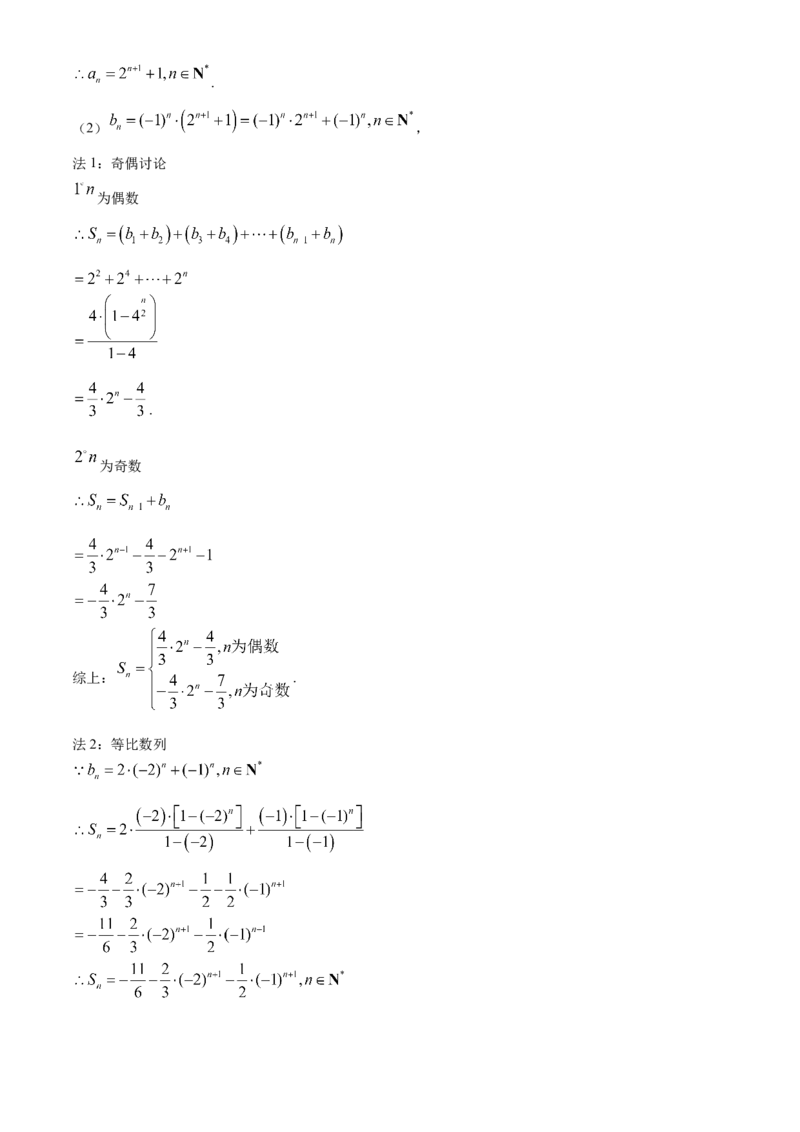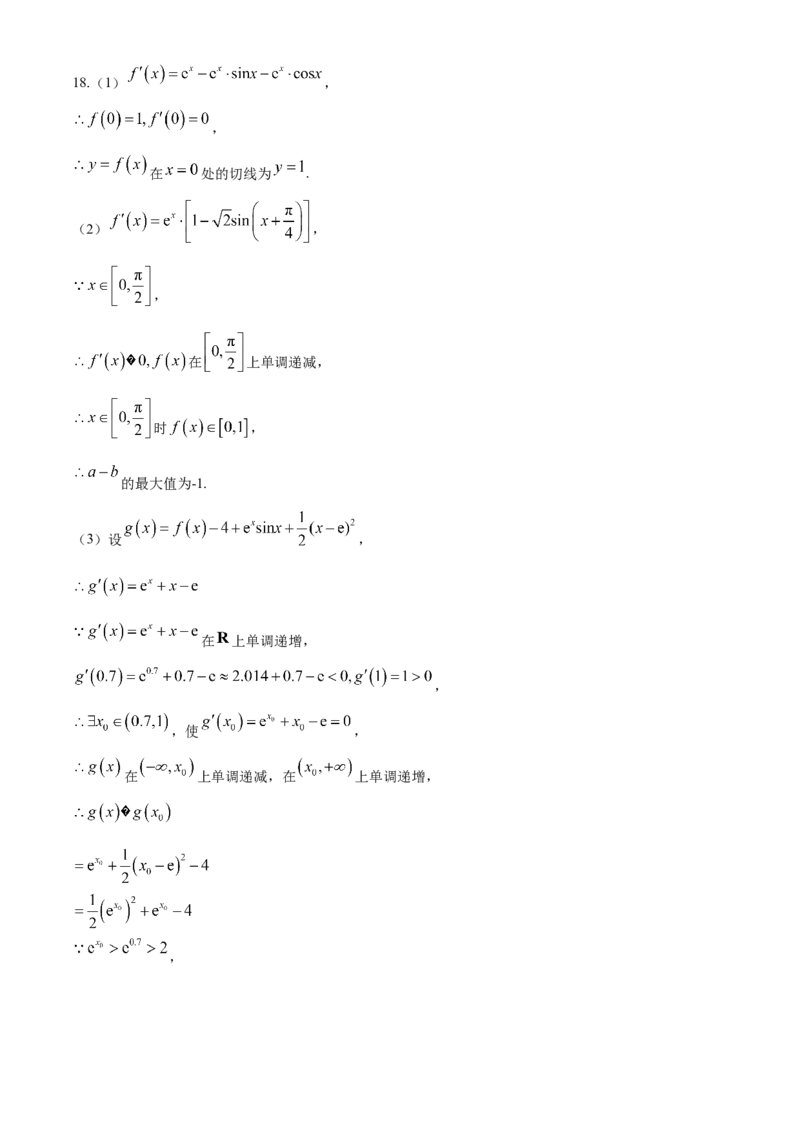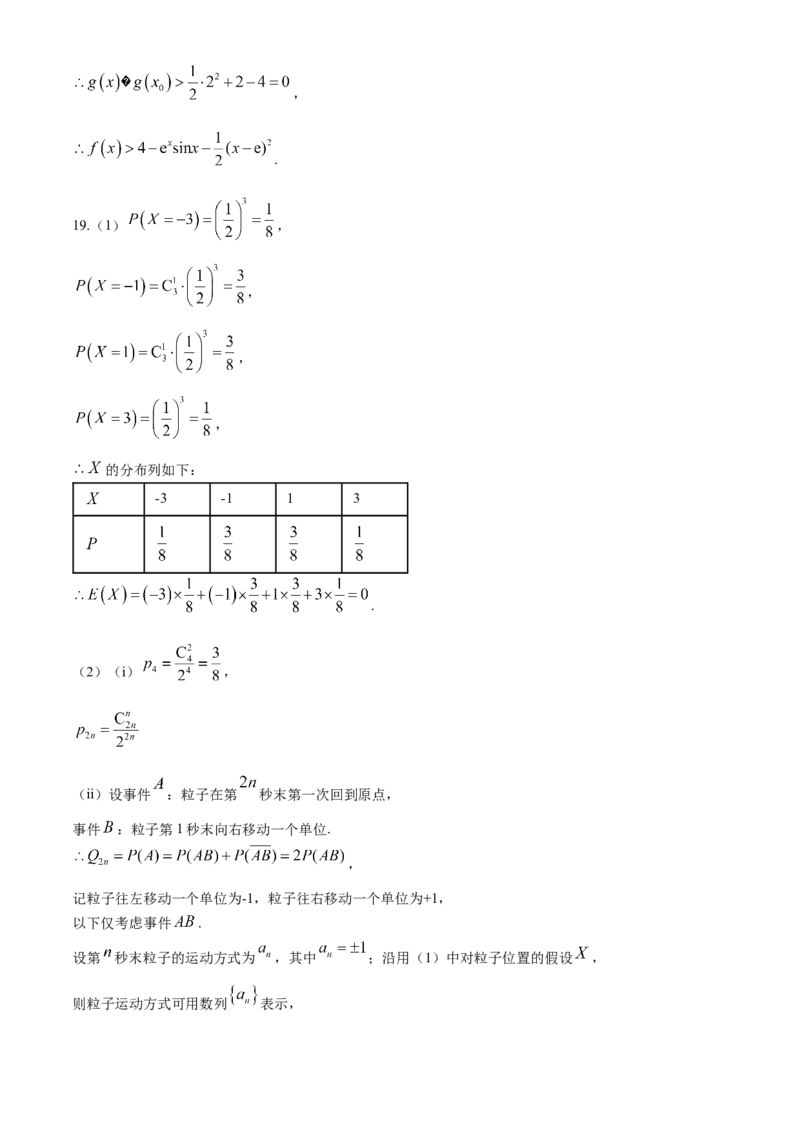文档内容
武汉市部分重点中学 2023—2024 学年度下学期期末联考
高二数学试卷
命审题单位:武钢三中数学学科组 审题单位:圆创教育研究中心 湖北省武昌实验中学
本试卷共4页,19题.满分150分.考试用时120分钟.
考试时间:2024年6月27日下午14:00—16:00
★祝考试顺利★
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码贴在答题
卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试
卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答
题卡上的非答题区域均无效.
4.考试结束后,请将本试卷和答题卡一并上交.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有
一项是符合题目要求的)
1.从含有3件正品,2件次品的产品中随机抽取2件产品,则抽取出的2件产品中恰有1件次品的概率为(
)
A. B. C. D.
2.已知随机变量 服从正态分布 ,则 ( )
A.0.1 B.0.2 C.0.4 D.0.8
3.若函数 在 处取得极值,则实数 的取值范围是( )
A. B. C. D.
4.函数 的图象大致为( )
A. B.C. D.
5.若函数 的图象与 的图象恰好有四个交点,则实数 的取值范围是
( )
A. B. C. D.
6.设某人在 次射击中击中目标的次数为 ,且 ,记 ,若
是唯一的最大值,则 的值为( )
A.7 B.7.7 C.8.4 D.9.1
7.已知 ,则( )
A. B.
C. D.
8.设函数 ,若存在实数 ,使得 ,则 的最
小值为( )
A. B.2 C.1 D.
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求,全部选对得6分,部分选对得部分分,有选错的得0分)
9.下列说法中,正确的命题是( )
A.两个随机变量的线性相关性越强,则相关系数 的绝对值越接近于1
B.
C.用不同的模型拟合同一组数据,则残差平方和越小的模型拟合的效果越好
D.随机变量 服从两点分布,且 ,设 ,则10.甲乙两人参加三局两胜制比赛(谁先赢满两局则获得最终胜利且比赛结束).已知在每局比赛中,甲赢
的概率为0.6,乙贏的概率为0.4,且每局比赛的输赢相互独立.若用 表示事件“甲最终获胜”, 表示
事件“有人获得了最终胜利时比赛共进行了两局”, 表示事件“甲赢下第三局”.则下列说法正确的是(
)
A. B.
C. 与 互斥 D. 与 独立
11.若直线 与曲线 ,相交于不同两点 ,曲线 在A,B点处
切线交于点 ,则( )
A. B.
C. D.不存在 ,使得
三、填空题(本大题共3小题,每小题5分,共15分)
12.已知离散型随机变量 的分布列为
0 1 2 3
若 ,则 __________.
13.已知函数 ,若 恒成立,则 的最小值为__________.
14.从 这10个数中随机抽一个数记为 ,再从 中随机抽一个数记为 ,则
__________.
四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本题满分13分)
已知命题 ,不等式 恒成立;命题 ,使 成
立.
(1)若命题 为真命题,求实数 的取值范围;
(2)若命题 中恰有一个为真命题,求实数 的取值范围.
16.(本题满分15分)随着社会经济的发展,越来越多的人在抵达目的地后选择租车游玩,拉动了许多租车公司的业务,某租车
公司为继续开拓市场,提升服务质量,迎接暑假旅游旺季的到来,对近5年的暑假的租车业务量 (单位:
十万元)进行了汇总研究,情况如下:
年份 2019年 2020年 2021年 2022年 2023年
业务量 20 24 36 43 52
经过数据分析,已知年份与业务量具有线性相关关系.
(1)假设2019年为第1年,求第 年的业务量 关于 的经验回归方程,并预测2024年暑假的业务量;
(2)该公司从2023年暑假租车的客户中随机抽取了100名客户进行调研,现将100名客户的年龄划分为
“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请将 列联表补充完整
并根据小概率值 的独立性检验,分析青年群体和中老年群体对租车服务的评价是否有差异.
好评 差评 合计
青年 20
中老年 15
合计 45 100
附:经验回归直线方程 ,其中
独立性检验中的 ,其中 .
临界值表:
0.050 0.010 0.001
3.841 6.635 10.828
17.(本题满分15分)
在数列 中, ,且 .
(1)求 的通项公式;
(2)令 ,求数列 的前 项和 .
18.(本题满分17分)已知函数 .
(1)求曲线 在 处的切线方程;
(2)若不等式 对任意 恒成立,求实数 的最大值;
(3)证明: .(参考数据: )
19.(本题满分17分)
Catalan数列(卡特兰数列)最早由我国清代数学家明安图(1692-1765)在研究三角函数幂级数的推导过
程中发现,成果发表于1774年出版的《割圜密率捷法》中,后由比利时数学家卡特兰(Catalan,1814-
1894)的名字来命名,该数列的通项被称为第 个Catalan数,其通项公式为
.在组合数学中,有如下结论:由 个+1和 个-1构成的所有数列
, 中,满“对任意 ,都有 ”的数列的个数等于 .
已知在数轴上,有一个粒子从原点出发,每秒向左或向右移动一个单位,且向左移动和向右移动的概率均
为 .
(1)设粒子第3秒末所处的位置为随机变量 (若粒子第一秒末向左移一个单位,则位置为-1;若粒子
第一秒末向右移一个单位,则位置为1),求 的分布列和数学期望 ;
(2)记第 秒末粒子回到原点的概率为 .
(i)求 及 ;
(ii)设粒子在第 秒末第一次回到原点的概率为 ,求 .武汉市部分重点中学 2023-2024 学年度下学期期末联考
高二数学试卷参考答案与评分细则
题号 1 2 3 4 5 6 7 8 9 10 11
答案 A D C D C A A C ACD ABC ABD
12. 13.-1 14.
15.(1)若命题 为真命题,则
,
.
(2)当 为真命题时:
,
.
当命题 中恰有一个为真命题时,
为真命题, 为假命题,即
.为假命题, 为真命题,即
.
综上: .
16.(1) ,
,
.
.
时, ,
预测2024年暑假的业务量约为59.9十万元.
(2)列联表如下:
好评 差评 合计
青年 20 30 50
中老年 35 15 50
合计 55 45 100
,
根据小概率值 的独立性检验,青年群体和中老年群体对租车服务的评价有差异.
17.(1) ,
是公比为2的等比数列.
,
,
,.
(2) ,
法1:奇偶讨论
为偶数
.
为奇数
综上: .
法2:等比数列18.(1) ,
,
在 处的切线为 .
(2) ,
,
在 上单调递减,
时 ,
的最大值为-1.
(3)设 ,
在 上单调递增,
,
,使 ,
在 上单调递减,在 上单调递增,
,,
.
19.(1) ,
,
,
,
的分布列如下:
-3 -1 1 3
.
(2)(i) ,
(ii)设事件 :粒子在第 秒末第一次回到原点,
事件 :粒子第1秒末向右移动一个单位.
,
记粒子往左移动一个单位为-1,粒子往右移动一个单位为+1,
以下仅考虑事件 .
设第 秒末粒子的运动方式为 ,其中 ;沿用(1)中对粒子位置的假设 ,
则粒子运动方式可用数列 表示,如: 表示粒子在前4秒按照右、右、左、左的方式运动.
由粒子在第 秒末第一次回到原点,可知
数列 的前 项中有 个1和 个-1.
,
,
粒子在余下 秒中运动的位置满足 ,
即 ,
粒子在余下 秒中运动方式的总数为 ,
,