湖北省重点高中智学联盟2025届新高三8月联考考试数学试卷答案_8月_240818湖北省重点高中智学联盟2025届新高三8月联考考试_湖北省重点高中智学联盟2025届新高三8月联考考试数学

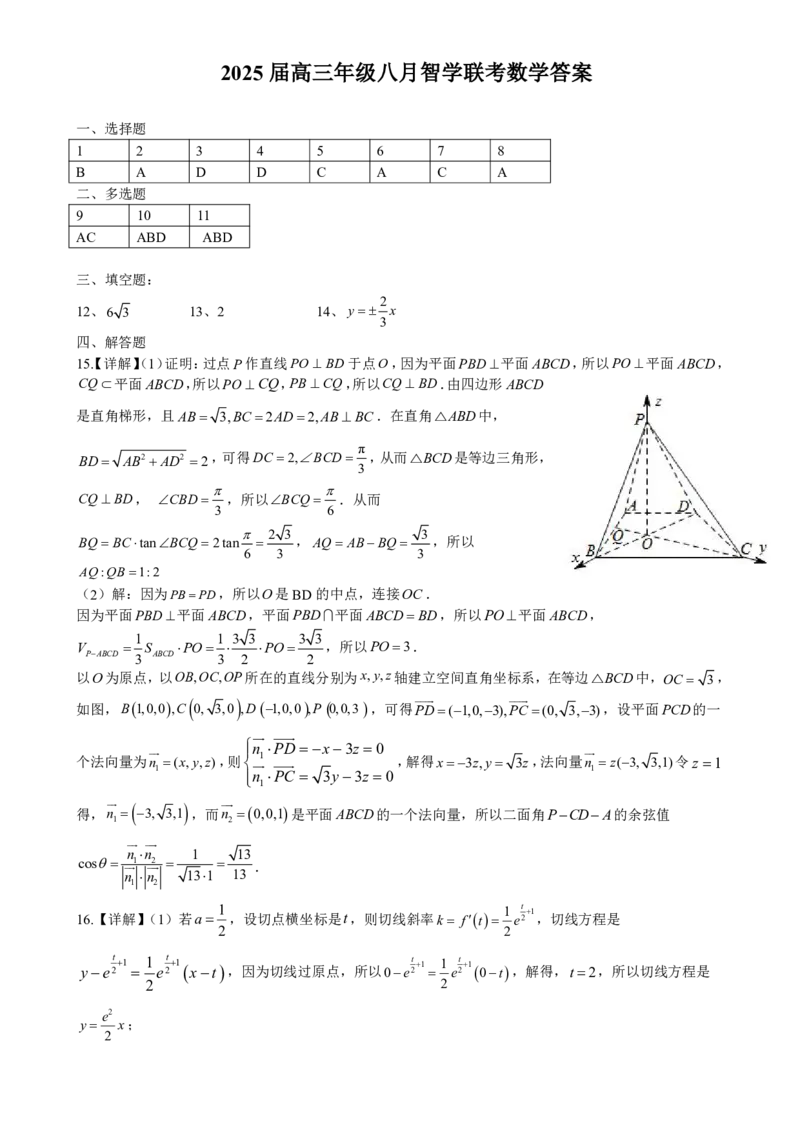
2025 届高三年级八月智学联考数学答案 一、选择题 1 2 3 4 5 6 7 8 B A D D C A C A 二、多选题 9 10 11 AC ABD ABD 三、填空题： 2 12、6 3 13、2 14、y x 3 四、解答题 15【. 详解】（1）证明：过点P作直线PO BD于点O，因为平面PBD平面ABCD，所以PO平面ABCD， CQ平面ABCD，所以PO CQ，PBCQ，所以CQBD．由四边形ABCD 是直角梯形，且AB 3,BC2AD2,ABBC．在直角△ABD中， π BD AB2AD2 2 ，可得DC 2,BCD ，从而△BCD是等边三角形， 3   CQBD， CBD ，所以BCQ ．从而 3 6  2 3 3 BQBCtanBCQ2tan  ，AQ ABBQ ，所以 6 3 3 AQ:QB1:2 （2）解：因为PBPD，所以O是BD的中点，连接OC． 因为平面PBD平面ABCD，平面PBD平面ABCDBD，所以PO平面ABCD， 1 1 3 3 3 3 V  S PO  PO ，所以PO3． PABCD 3 ABCD 3 2 2 以O为原点，以OB,OC,OP所在的直线分别为x,y,z轴建立空间直角坐标系，在等边△BCD中，OC  3， 如图，B1,0,0,C  0, 3,0  ,D 1,0,0,P 0,0,3 ，可得  P  D  (1,0,3),  P  C  (0, 3,3)，设平面PCD的一     n PD x3z  0  个法向量为n (x,y,z)，则 1  ，解得x3z,y 3z，法向量n  z(3, 3,1)令z 1 1 1 n PC  3y3z 0 1   得，n   3, 3,1  ，而n 0,0,1是平面ABCD的一个法向量，所以二面角PCDA的余弦值 1 2   n n 1 13 cos 1 2   ． n n 131 13 1 2 16.【详解】（1）若a 1 ，设切点横坐标是t，则切线斜率k  ft 1 e2 t 1，切线方程是 2 2 ye2 t 1  1 e2 t 1 xt ，因为切线过原点，所以0e2 t 1  1 e2 t 10t，解得，t2，所以切线方程是 2 2 e2 y x； 2（2）首先注意到 f  0 e，g  x eax12xe，x 0，g x aeax12， ①若a0，则g x 0在x0时恒成立，故g  x  单调递减，则对所有x0，g  x  g  0 0，不满 足题意，故舍去；  2 1 2  1 2  ②若a0，则g x aeax1 ，令g x  <0得，x ln 1；令g x  >0得，x ln 1．所  a a a  a a   1 2  1 2   以，g  x  在, ln 1上单调递减，g  x  在 ln 1,上单调递增．  a a  a a   （ⅰ）若0a 2 ，则ln 2 1，即 1 ln 2 1  0，所以g  x  在  0, 1 ln 2 1    上单调递减， e a a a   a a  1 2   1 2   ln 1,上单调递增，则g  x   f  ln 1  f  0  0不满足题意，故舍去； a a   min a a  （ⅱ）若a 2 ，则ln 2 1，即 1 ln 2 1  0，所以g  x  在0,上单调递增，则对所有x0， e a a a  g  x  f  0 0，符合题意． 2  综上所述，a的取值范围是  ,． e  1 17.【详解】（1）由题意PX 305 1PX 1 10.68270.84135，若某天该商场有200 2 位顾客，估计该天消费额X 在305，内的人数为0.84135200168.27168；  3  3 1 （2）设X的取值为0，10，20，则P(X 0)  1   1   ，  4  4 16 3 1 1 1 3 1 1 5 5 P(X 10)        ，P(X 2)1P(X 0)P(X 1) ，所以X的分 4 3 3 4 4 3 3 48 6 布列为： X 0 10 20 1 5 5 P 16 48 6 1 5 5 425 数学期望E(X)0 10 20  ． 16 48 6 24 ac1  18.【详解】（1）由椭圆上的点到焦点的最近距离是1，故ac1，则 a2b2  7，解得a2，b 3，  a2 b2c2  c1，即椭圆E的方程为 x2  y2 1；（2）设Bx，y 、Cx ,y ，由题可知，A2，0，则k  y 1 ， 4 3 1 1 2 2 1 x 1 2y y y k 2  x  2 2 ，所以k 1 k 2  xx 2 1 x 2 x 4 ①.由题意，设BC所在的直线方程为ykx4，联立 2 1 2 1 2 ykx4  x2 y2 可得，  34k2 x232k2x64k2120，且  32k22 4  4k23  64k212  0 ，解得   1  4 3 0 k  1 依据韦达定理，x x  32k2 ，x x  64k212 ，设直线AB的方程为y y 1 x2 ，直线 2 1 2 34k2 1 2 34k2 x 2 1 AC的方程为y y 2 x2 ，则依题设，M  4， 6y 1  、N  4， 6y 2  ，y kx 4，y kx 4， x 2  x 2  x 2 1 1 2 2 2 1 2 6y 6y 6yx 12y 6y x 12y 36kx 36k x x 则 MN  1  2  1 2 1 2 1 2  1 2  36k  1 2 ，即 x 2 x 2 xx 2x x 4 xx 2x x 4 xx 2x x 4 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1024k4 256k2 48  x x 2 4xx  34k2 34k2 MN  36k  1 2 1 2  36k  ，化简得 xx 2x x 4 144k2 1 2 1 2 34k2 144576k2 14k2 1 1 1 MN  36k  3 3 4，依题设， MN 3 4 3 5，所以k  ，满足 144k2 k2 k2 k2 3 1 0 k  合题意． 2 1 综上所述，直线的斜率k  ． 3 19.【详解】（1）a 有三种结果： 1，1，2，2或1，2，2，2或1，2，4，2； n a a a （1）当m2025时，n2,3,,2024．由a 1,1 2 2,,1 n1 2,1 n 2，累乘得1a 2n1①； 1 a a a n 1 n2 n1 a a a a 又由1 n 2,，1 n1 2,,1 2023 2,1 2024 2,1a a ，累乘得1a 22025na ②；将① a a a a 2025 2025 n 2025 n1 n2 2024 2025 ②相乘得1a2 22024a ，又a N*，a 16，所以1a 21014. 所以数列a 的最大项的最大值为21014， n 2025 n 2025 n n  2n1 n1,2,,1015 满足条件的数列为a  ； n 22029n n1016,1017,,2025 （3）①讨论项数满足1  k  M 的情况： a 因为数列{a }满足：当1nM 1时1 n1 2，a 1，所以0a 2，又因为当1iM 1，都有a N， n a 1 2 i n 所以a 1或a 2，当a 2时，a a 2，此时a a 2a a ，这与在剩下的项中总存在满足 2 2 2 4 3 1 2 3 4 1 pqM的项a 和a ，使得a a a a 矛盾，所以a 1，类似的，必有a 1，a 1，a 2，a 2， p q s t p q 2 3 4 5 6 由a a a a 得前6项任意两项之积小于等于4时，均符合，要使得m值要尽量小，则需要每项尽可能 s t p q大，且则a a 4a a ，a 22，同理，a 23，a 24，，a 22023，由对称性得最后6项为 5 6 1 7 7 8 9 M6 a a a a 22025，a a 22024，当{a }中间各项为公比为2的等比数列时，可使得M值 M M1 M2 M3 M4 M5 n 最小，且M的最小值为M 6202262034，满足已知条件． min ②讨论项数满足M k m的情况： 类比①可知a a  a  a 22025，a a 22024，a 22023，a 22022，，a 23， M M1 M2 M3 M4 M5 M6 M7 m7 a 22，a 2，a 2，a a a a 20 1． m6 m5 m4 m3 m2 m1 m 综上所述，m的最小值m 2034214067．故答案为：4067． min