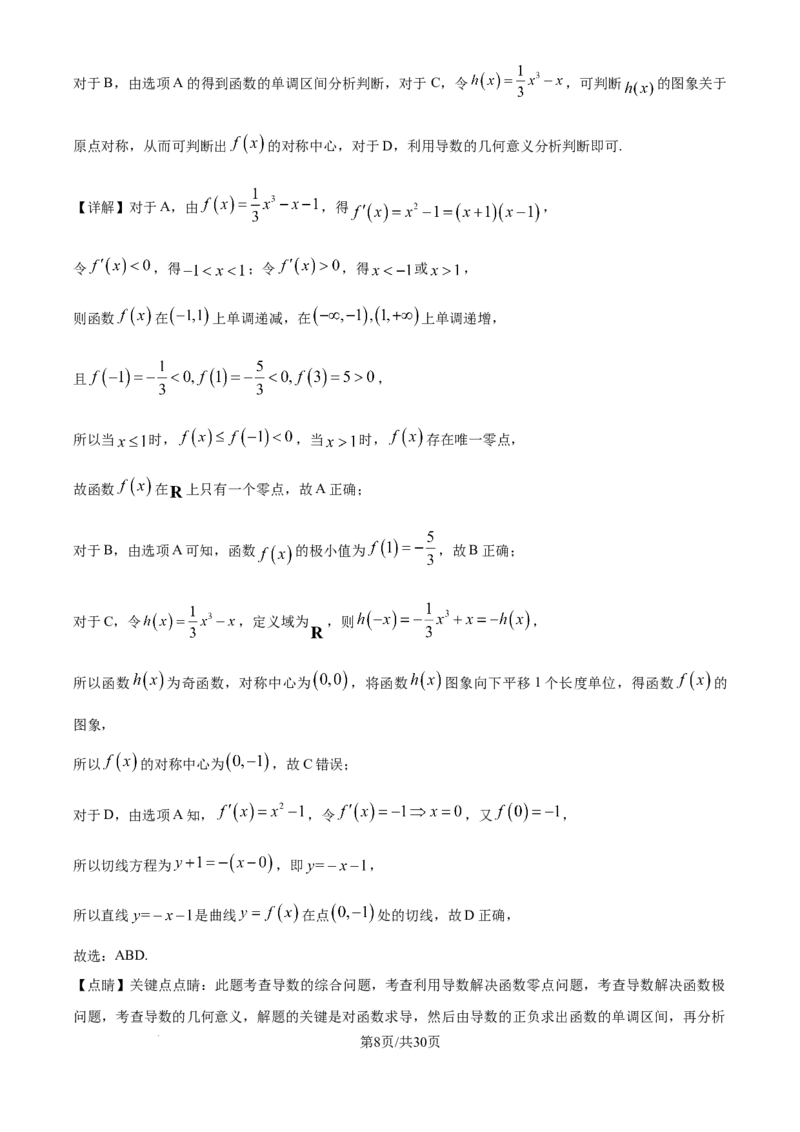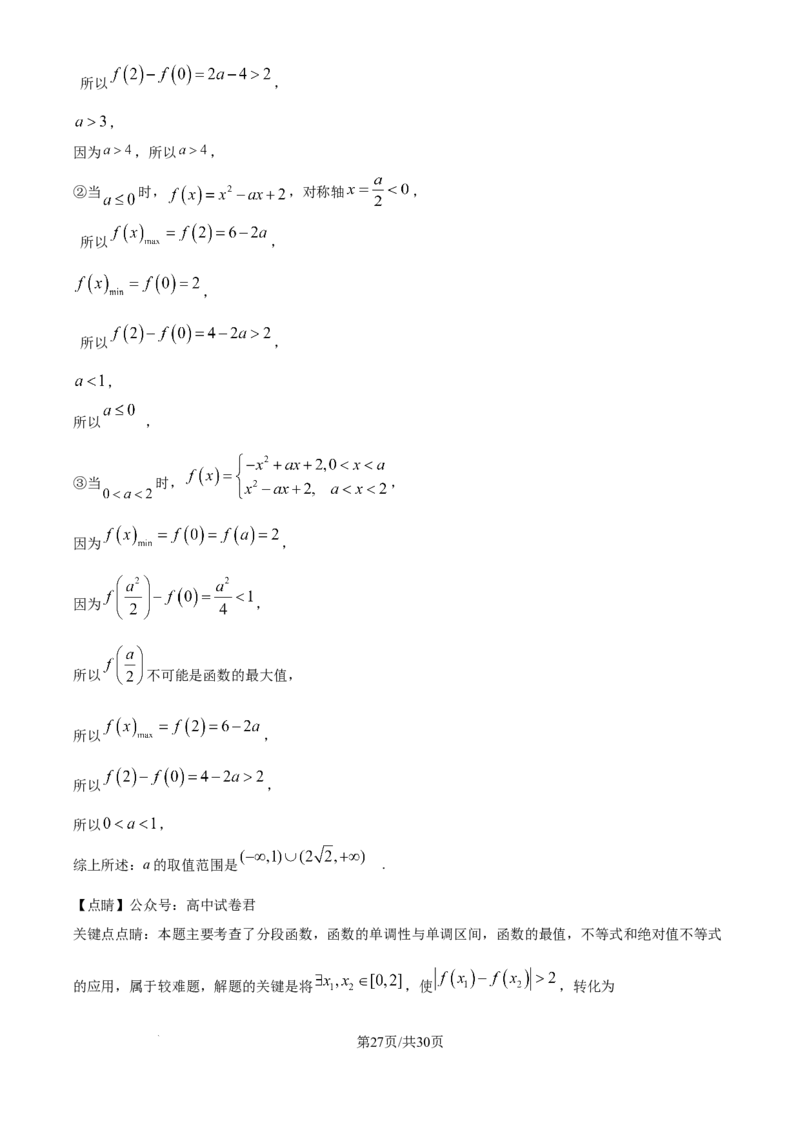文档内容
邵阳市第二中学 2022 级高三第一次月考数学试卷
时间:120分钟 满分:150分
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的)
1. 若非空集合A,B满足 ,U为全集,则下列集合中表示空集的是( )
A. ; B. ; C. ; D. .
【答案】D
【解析】
【分析】根据 图,对各个选项逐一分析,即可求得正确答案.
【详解】根据 可以看出
对A, ;
对B, ;
对C, ;
对D, .
故选:D
2. sin40°(tan10°-√3)=
A. - B. -1 C. D. -
【答案】B
【解析】
【分析】利用三角函数的切化弦及化一公式、诱导公式化简即可求解.
【详解】解:
第1页/共30页
学科网(北京)股份有限公司故选B.
【点睛】本题主要考查了三角函数的切化弦及化一公式、诱导公式的综合应用.
3. 已知函数 的定义域是 ,则函数 的定义域为( )
A. B.
C. D.
【答案】A
【解析】
【分析】由函数定义域的概念及复合函数定义域的求解方法运算求解即可.
【详解】因为函数 的定义域是 ,所以 ,
所以 ,所以函数 的定义域为 ,
所以要使函数 有意义,则有 ,解得 ,
第2页/共30页
学科网(北京)股份有限公司所以函数 的定义域为 .
故选:A.
4. 下列求导数计算错误的是( )
A. B.
C. D.
【答案】B
【解析】
【分析】利用导数的运算法则及简单复合函数求导法则计算即可.
【详解】解:A. ,正确,不符合题意;
B. ,错误,符合题意;
C. ,正确,不符合题意;
D. ,正确,不符合题意.
故选:B.
5. 苏格兰数学家纳皮尔(J. Napier,1550-1617)发明的对数及对数表(如下表),为当时的天文学家处
理“大数”的计算大大缩短了时间.即就是任何一个正实数N可以表示成 ,则
,这样我们可以知道N的位数.已知正整数 是35位数,则M的值为(
)
N 2 3 4 5 11 12 13 14 15
.
0.30 0.48 0.60 070 1.04 1.08 1.11 1.15 1.18
A. 3 B. 12 C. 13 D. 14
第3页/共30页
学科网(北京)股份有限公司【答案】C
【解析】
【分析】根据所给条件列出不等式,结合对数的运算即可求解.
【详解】由题意可知 ,两边同时取对数可得 ,
所以 ,故 ,则 ,
由表中数据可知 ,
故选:C
6. 一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买 黄金,售货员先将 的砝码放
在天平左盘中,取出一些黄金放在天平右盘中使天平平衡;再将 的砝码放在天平右盘中,再取出一些黄
金放在天平左盘中使天平平衡;最后将两次称得的黄金交给顾客.你认为顾客购得的黄金( )
附:依据力矩平衡原理,天平平衡时有 ,其中 、 分别为左、右盘中物体质量, 、
分别为左右横梁臂长.
A. 等于 B. 小于 C. 大于 D. 不确定
【答案】C
【解析】
【分析】设天平左臂长 ,右臂长 ,且 ,根据已知条件求出 、 的表达式,利用基本不等式
比较 与 的大小关系,即可得出结论.
【详解】设天平左臂长 ,右臂长 ,且 ,
设天平右盘有 克黄金,天平左盘有 克黄金,所以 ,
所以 , ,则 .
故选:C.
第4页/共30页
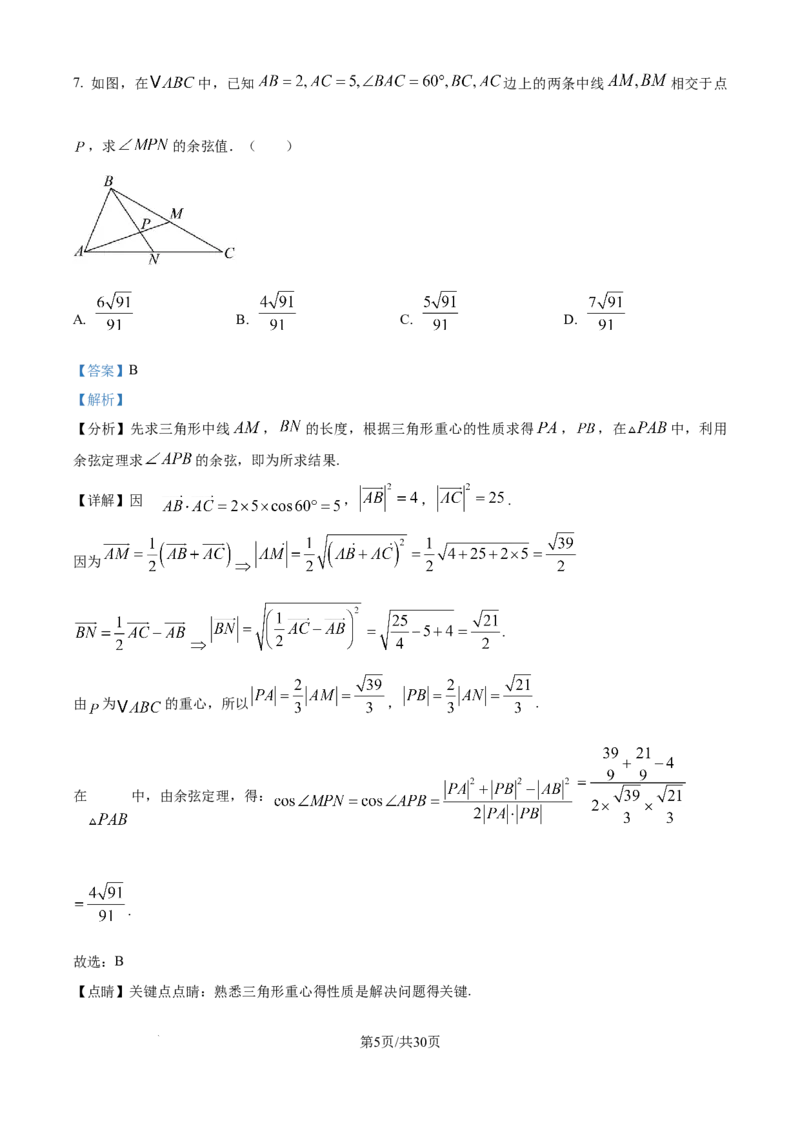
学科网(北京)股份有限公司7. 如图,在 中,已知 边上的两条中线 相交于点
,求 的余弦值.( )
A. B. C. D.
【答案】B
【解析】
【分析】先求三角形中线 , 的长度,根据三角形重心的性质求得 , ,在 中,利用
余弦定理求 的余弦,即为所求结果.
【详解】因 , , .
为
因为
.
由 为 的重心,所以 , .
在 中,由余弦定理,得:
.
故选:B
【点睛】关键点点睛:熟悉三角形重心得性质是解决问题得关键.
第5页/共30页
学科网(北京)股份有限公司8. 已知直线 是曲线 的切线,也是曲线 的切线,则k的最大值是(
)
A. B. C. 2e D. 4e
【答案】B
【解析】
【分析】设切点分别为 和 ,则 ,根据题意转化为
有解,设 ,求得 ,得出函数的单调性和极
小值 ,结合 ,即可求解.
【详解】因为 是 和 的公切线,
设切点分别为 和 ,则 ,
由 ,可得 ,则
又由 ,可得 ,且 ,则 ,
所以 ,可得 ,
即 ,显然 同号,不妨设 ,
设 ,(其中 ),
第6页/共30页
学科网(北京)股份有限公司可得 ,令 ,可得 ,
当 时, , 单调递减;
当 时, , 单调递增,
要使得 有解,则需要 ,即
即 ,解得 ,所以 ,即 的最大值为 .
故选:B.
【点睛】方法技巧:对于利用导数研究不等式的恒成立与有解问题的求解策略:
1、通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;
2、利用可分离变量,构造新函数,直接把问题转化为函数的最值问题.
3、根据恒成立或有解求解参数的取值时,一般涉及分离参数法,但压轴试题中很少碰到分离参数后构造
的新函数能直接求出最值点的情况,进行求解,若参变分离不易求解问题,就要考虑利用分类讨论法和放
缩法,注意恒成立与存在性问题的区别.
二、多选题(本题共三小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求的.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9. 已知函数 ,则( )
A. 有一个零点 B. 的极小值为
C. 的对称中心为 D. 直线 是曲线 的切线
【答案】ABD
【解析】
【分析】对于A,由函数求导后,由导数的正负可求出函数的单调区间,再结合零点存在性定理分析判断,
第7页/共30页
学科网(北京)股份有限公司对于B,由选项A的得到函数的单调区间分析判断,对于C,令 ,可判断 的图象关于
原点对称,从而可判断出 的对称中心,对于D,利用导数的几何意义分析判断即可.
【详解】对于A,由 ,得 ,
令 ,得 ;令 ,得 或 ,
则函数 在 上单调递减,在 上单调递增,
且 ,
所以当 时, ,当 时, 存在唯一零点,
故函数 在 上只有一个零点,故A正确;
对于B,由选项A可知,函数 的极小值为 ,故B正确;
对于C,令 ,定义域为 ,则 ,
所以函数 为奇函数,对称中心为 ,将函数 图象向下平移1个长度单位,得函数 的
图象,
所以 的对称中心为 ,故C错误;
对于D,由选项A知, ,令 ,又 ,
所以切线方程为 ,即 ,
所以直线 是曲线 在点 处的切线,故D正确,
故选:ABD.
【点睛】关键点点睛:此题考查导数的综合问题,考查利用导数解决函数零点问题,考查导数解决函数极
问题,考查导数的几何意义,解题的关键是对函数求导,然后由导数的正负求出函数的单调区间,再分析
第8页/共30页
学科网(北京)股份有限公司判断,考查计算能力,属于较难题.
10. 设点D是 所在平面内一点,O是平面上一个定点,则下列说法正确的有( )
A. 若 ,则D是BC边上靠近B的三等分点
B. 若 ,( 且 ),则直线AD经过 的垂心
C. 若 ,且x, , ,则 是 面积的一半
D. 若平面内一动点P满足 ,( 且 ),则动点P的轨迹一定通过
的外心
【答案】ABC
【解析】
【分析】对于A,化简等式成 ,即可判断;对于B,将等式两边与 作点乘,化简得出结果
为0即可判断;对于C,利用平面向量基本定理推出三点共线,结合图形和共线向量即得结论;对于D,
化简向量等式,利用单位向量作出 即得菱形,推得 ,即得结论.
【详解】对于A,由 可得, ,
即得 ,故点D是BC边上靠近B的三等分点,故A正确;
对于B,因 ,则
第9页/共30页
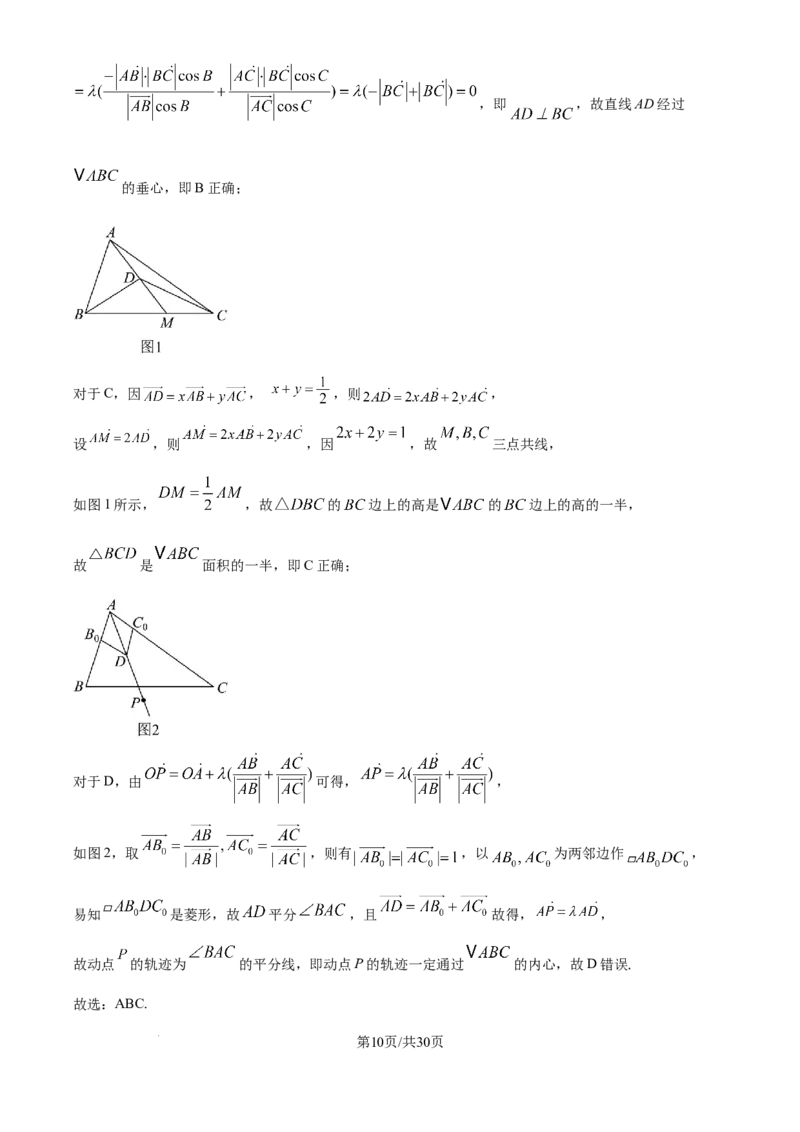
学科网(北京)股份有限公司,即 ,故直线AD经过
的垂心,即B正确;
对于C,因 , ,则 ,
设 ,则 ,因 ,故 三点共线,
如图1所示, ,故 的 边上的高是 的 边上的高的一半,
故 是 面积的一半,即C正确;
对于D,由 可得, ,
如图2,取 ,则有 ,以 为两邻边作 ,
易知 是菱形,故 平分 ,且 故得, ,
故动点 的轨迹为 的平分线,即动点P的轨迹一定通过 的内心,故D错误.
故选:ABC.
第10页/共30页
学科网(北京)股份有限公司【点睛】关键点点睛:本题主要考查平面向量的线性运算和数量积的应用,属于难题.
对于向量等式,要结合图形,和选项的启发,有时从构造平面向量基本定理的条件入手;有时通过与其他
向量的点乘为0判断线线垂直;有时通过两单位向量的和作平行四边形,推得菱形.
11. 设函数 向左平移 个单位长度得到函数 ,已知 在 上有且
只有5个零点,则下列结论正确的是( )
A. 的图象关于直线 对称
B. 在 上,方程 的根有3个,方程 的根有2个
C. 在 上单调递增
D. 的取值范围是
【答案】CD
【解析】
【分析】根据函数的零点的个数,求出参数 的范围,再判断函数的单调性、对称性和方程根的个数.
【详解】由题意, ,
由题意, 不一定是函数的对称轴,所以A错误;
当 时,得 ,故 ;
,所以D正确.
因为 ,则 的根分别可由 或 或 求出,
共有3个根;
当 时, 的根分别可由 或 求出,共2个根;
第11页/共30页
学科网(北京)股份有限公司当 时, 的根分别可由 或 或 求
出,共3个根;所以B错误;
当 时,得 ,
由 ,得 ,所以 ,此时 在 上单调递增,所以
C正确.
故选:CD.
【点睛】本题重点考查三角函数 的图象与性质,难度较大,做题时注意利用整体法
判断:即通过将 作为整体,借助 的图象和性质来进行判断.公众号:高中试卷君
三、填空题(本大题共3小题,每小题5分,共15分)
12. 出入相补是指一个平面(或立体)图形被分割成若干部分后面积(或体积)的总和保持不变,我国汉
代数学家构造弦图,利用出入相补原理证明了勾股定理,我国清代的梅文鼎、李锐、华蘅芳、何梦瑶等都
通过出入相补原理创造了不同的面积证法证明了勾股定理.在下面两个图中,若 , ,
,图中两个阴影三角形的周长分别为 , ,则 的最小值为________.
【答案】
【解析】
第12页/共30页
学科网(北京)股份有限公司【分析】根据图形中的相似关系先表示出 ,然后利用基本不等式求解出最小值.
【详解】如图1,易知 ,且 ,
所以 ,所以 ;
如图2,易知 ,且 ,
所以 ,所以 ,
所以 ,
又因为 ,所以 ,当且仅当 时取等号,
所以 ,
所以最小值为 ,
第13页/共30页
学科网(北京)股份有限公司故答案为: .
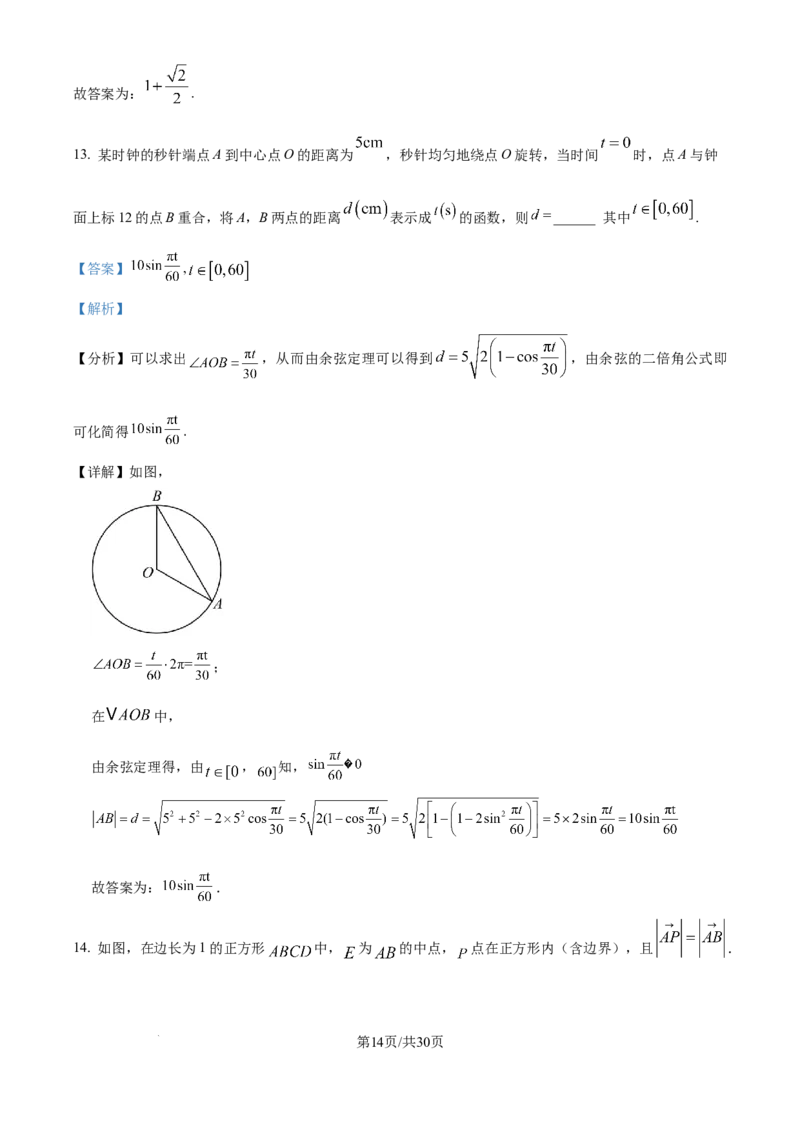
13. 某时钟的秒针端点A到中心点O的距离为 ,秒针均匀地绕点O旋转,当时间 时,点A与钟
面上标12的点B重合,将A,B两点的距离 表示成 的函数,则 ______ 其中 .
【答案】 ,
【解析】
【分析】可以求出 ,从而由余弦定理可以得到 ,由余弦的二倍角公式即
可化简得 .
【详解】如图,
;
在 中,
由余弦定理得,由 , 知,
故答案为: .
14. 如图,在边长为1的正方形 中, 为 的中点, 点在正方形内(含边界),且 .
第14页/共30页
学科网(北京)股份有限公司①若 ,则 的值是_______;②若向量 ,则 的最小值为
________.
【答案】 ①. ##0.5 ②. ##0.5
【解析】
【分析】①由题知 是边长为1的等边三角形,进而根据向量数量积求解即可;
②考虑到该题为高一题目,不能使用导数,故提供了另一种解法,法二仅供参考.
法一:结合图像,作 ,连接PF,设 ,利用 三点共线可得
,又 三点共线,故可得 ,因此只需要考虑 值最大的情况即可
得到 的最小值.
法二:由题知点 的轨迹为以 为圆心, 为半径的圆在正方体 内的圆弧部分,进而建立直角
坐标系,设点 ,再利用向量坐标运算得
,进而构造函数,利用导数研究函数最值即可得答案.
【详解】解:①因为 , ,
第15页/共30页
学科网(北京)股份有限公司所以 是边长为1的等边三角形,
.
所以
②法一:如图,作 ,连接PF,设 ,
由于 共线,不妨设 ,又
故 ,
又由于 共线,所以 ,故 ,
结合图像可知,当 两点重合时, 交于 处,此时 值最大,
易知 ,故 ,故 .
.
法二:因为 ,
所以点 的轨迹为以 为圆心, 为半径的圆在正方体 内的圆弧部分,
第16页/共30页
学科网(北京)股份有限公司所以以点 为坐标原点,如图建立坐标系,
因为正方体 的边长为 ,
所以设点 , ,
所以由 得 ,
所以 ,解得 ,
所以 ,
令 ,
所以
因为 ,所以 ,
所以 区间 恒成立,
在
所以函数 在区间 单调递增,
所以 ,
所以 的最小值为 .
故答案为: ; .
第17页/共30页
学科网(北京)股份有限公司.
【点睛】本题考查向量坐标运算,数量积运算,导数求解函数最值,考查运算求解能力,是难题;本题第
二空解题的关键在于灵活利用向量共线的性质与结论,将 转化为 ,进而考虑特殊位置
点即可;而法二,将利用了导数的知识,根据题意设点 ,进而利用坐标运算
得 ,再结合函数性质求解最值即可.
四、解答题(本题共5小题,共77分,解答应写出文字说明,证明过程或演算步骤)
15. 在 中,内角 的对边分别为a,b,c,且 .
(1)求 的值;
(2)若 ,点 是线段 上的一点, , ,求 的值.
【答案】(1)
(2)
【解析】
【分析】(1)由正弦定理及三角恒等变换即可求解;
第18页/共30页
学科网(北京)股份有限公司(2)由 的面积比值得 (角平分线定理),设 ,则
, , ,再通过余弦定理列式即可求解.
【小问1详解】
因为 ,
由正弦定理得 ,
所以
.
即 ,
由正弦定理得 ,
又 、 ,则 或 (舍去).
所以 .
【小问2详解】
因为 ,设 中 边上的高为 ,
所以 ,所以 ,
设 ,
由 , , ,
第19页/共30页
学科网(北京)股份有限公司所以 ,则 , , ,
在 中,由余弦定理得 ,
设 的中点为 ,连接 ,
如图所示,由 ,则 ,
在 中, ,
所以 ,
解得 或 (舍去),
所以 .
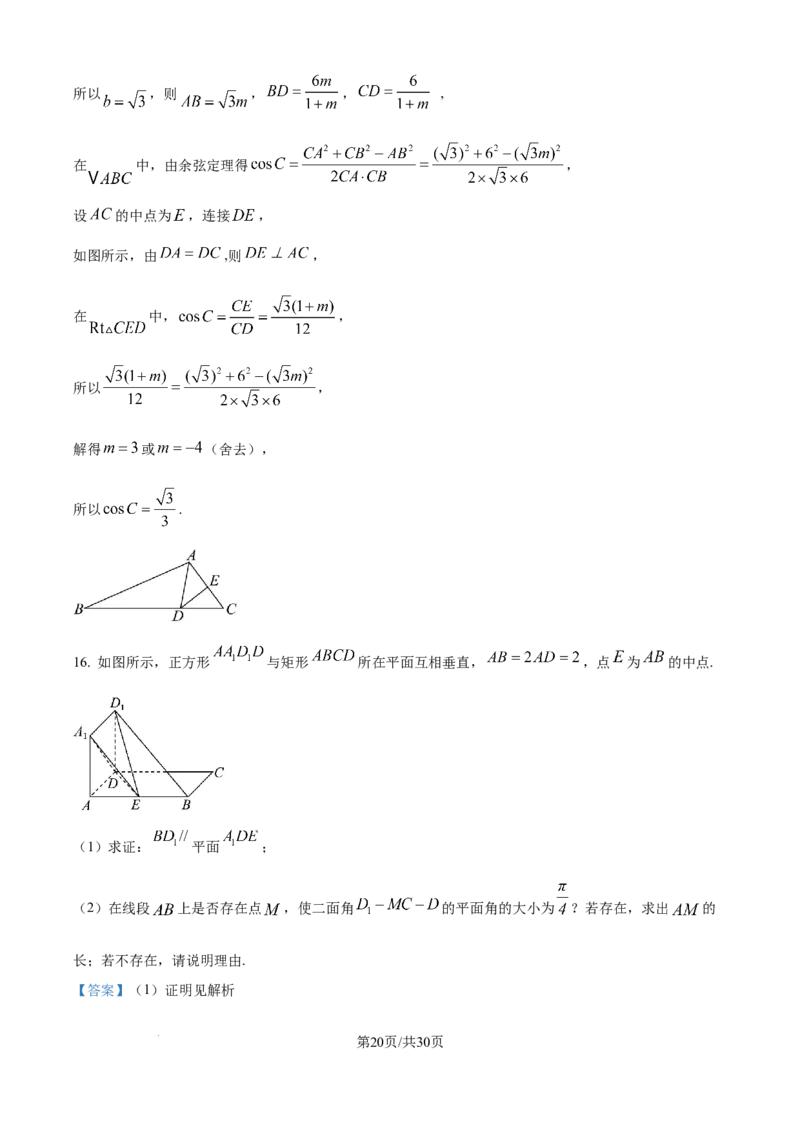
16. 如图所示,正方形 与矩形 所在平面互相垂直, ,点 为 的中点.
(1)求证: 平面 ;
(2)在线段 上是否存在点 ,使二面角 的平面角的大小为 ?若存在,求出 的
长;若不存在,请说明理由.
【答案】(1)证明见解析
第20页/共30页
学科网(北京)股份有限公司(2)存在,
【解析】
【分析】(1)由面面垂直的性质得 平面 ,以 为坐标原点, 所在直线分别
为 轴、 轴、 轴,建立空间直角坐标系,求出平面 的法向量、 ,利用 可得答案;
(2)假设在线段 上存在点 ,设 ,求出平面 、平面 的一个法
向量,由二面角的向量求法可得答案.
【小问1详解】
平面 平面 ,
平面 平面 ,
平面 平面 ,
则以 为坐标原点, 所在直线分别为 轴、 轴、 轴,
建立如图所示的空间直角坐标系 ,则
.
,
设平面 的法向量为⃗n =(x ,y ,z ),则 ,
1 1 1 1
令 ,解得: ,
又 ,即 ,
又 平面 平面 ;
【小问2详解】
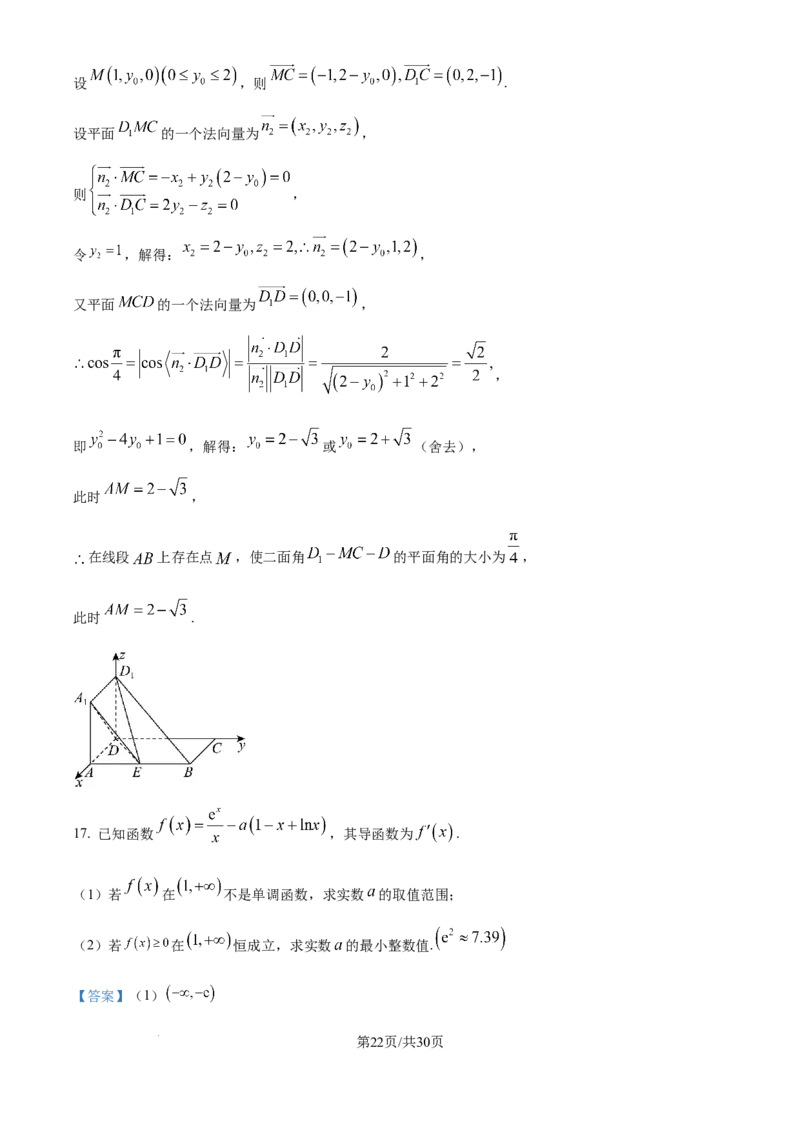
假设在线段 上存在点 ,使二面角 的大小为 .
第21页/共30页
学科网(北京)股份有限公司设 ,则 .
设平面 的一个法向量为 ,
则 ,
令 ,解得: ,
又平面 的一个法向量为 ,
,
即 ,解得: 或 (舍去),
此时 ,
在线段 上存在点 ,使二面角 的平面角的大小为 ,
此时 .
17. 已知函数 ,其导函数为 .
(1)若 在 不是单调函数,求实数 的取值范围;
(2)若 在 恒成立,求实数 的最小整数值.
【答案】(1)
第22页/共30页
学科网(北京)股份有限公司(2)
【解析】
【分析】(1)求出函数的导数,根据题意可知f′(x)在(1,+∞)有变号零点,由此结合函数的单调性,解不
等式即可求得答案;
(2)法一:采用分离参数法,将原不等式变为即为 在(1,+∞)恒成立,构造函数
,求函数的导数,利用导数求其最小值,即可求得答案;
法二:求函数 的导数,利用导数判断其单调性,求得函数最小值,结合解不等
式即可求得答案.
【小问1详解】
;
因为 在(1,+∞)不是单调函数,所以f′(x)在(1,+∞)有变号零点;
因为 恒成立,令 ,则 在(1,+∞)有变号零点;
因为 ,所以 在(1,+∞)单调递增,
因为 ,当 的值趋近正无限大时, 趋近于正无限大,a为待定的参数,
故 趋近于正无限大,故只需 ,即 ,
所以实数 的取值范围是 .
【小问2详解】
第23页/共30页
学科网(北京)股份有限公司(法一)令 ,
因为 在(1,+∞)恒成立,所以φ(x)在(1,+∞)单调递减,
所以 ,
所以 在(1,+∞)恒成立,即为 在(1,+∞)恒成立,
令 ,
则
,
令 ,则 在(1,+∞)恒成立,
所以ℎ(x)在(1,+∞)单调递减;
因为 ;
所以ℎ(x)有唯一零点 ,且
当 时,ℎ(x)>0,即 ,所以 在 单调递增;
当x∈(x
0
,+∞)时,ℎ(x)<0,即 ,所以 在 单调递减;
所以 ;
所以实数 的最小整数值为 .
(法二)
第24页/共30页
学科网(北京)股份有限公司由(1)得,当 时, 在(1,+∞)上单调递增,
所以 成立.
当 时,存在 ,使得
当 时,f′(x)<0,当x∈(x ,+∞)时,f′(x)>0,
0
所以 在 上单调递减,在 上单调递增;
所以 ,
令 得 ;
解之得 .
综上, ,
所以实数 的最小整数值为 .
【点睛】方法点睛:解决不等式恒成立问题,常用方法有:(1)将原不等式变形整理,分离参数,继而
构造函数,转化为求解函数的最值问题解决;(2)直接构造函数,求导数,求解函数的最值,使得最小
值恒大于(或大于等于)0或恒小于(或小于等于)0,解不等式即可.
18. 已知函数
(1)当 时,求 的单调增区间;
(2)若 ,使 ,求实数a的取值范围.
【答案】(1)单调递增区间为 和
(2)
【解析】
【分析】(1)根据已知及分段函数,函数的单调性与单调区间的计算,求出 的单调增区间;(2)
第25页/共30页
学科网(北京)股份有限公司根据已知及二次函数的性质求最值,结合不等式和绝对值不等式的计算求出实数a的取值范围.
【小问1详解】
当 时, ,
时, 单调递增,
时, 在 上单调递增,在 上单调递减,
所以 的单调递增区间为 和 ,
【小问2详解】
,使
所以 ,
即 ,
①当 时, ,对称轴 ,
当 即 时, ,
,
所以 ,
所以 或 ,
因为 ,所以 ,
当 即 时, ,
,
第26页/共30页
学科网(北京)股份有限公司所以 ,
,
因为 ,所以 ,
②当 时, ,对称轴 ,
所以 ,
,
所以 ,
,
所以 ,
③当 时, ,
因为 ,
因为 ,
所以 不可能是函数的最大值,
所以 ,
所以 ,
所以 ,
综上所述:a的取值范围是 .
【点睛】公众号:高中试卷君
关键点点睛:本题主要考查了分段函数,函数的单调性与单调区间,函数的最值,不等式和绝对值不等式
的应用,属于较难题,解题的关键是将 ,使 ,转化为
第27页/共30页
学科网(北京)股份有限公司,然后分类利用二次函数的性质求出其最值即可,考查了分类思想和计算能力
19. 如果数列 满足: 且 则称
为n阶“归化”数列.
(1)若某3阶“归化”数列 是等差数列,且单调递增,写出该数列的各项;
(2)若某11阶“归化”数列 是等差数列,求该数列的通项公式;
(3)若 为n阶“归化”数列,求证
【答案】(1)
(2)
(3)证明见解析
【解析】
【分析】(1)设 成公差为r的等差数列,显然 ,由 得到 ,
由 得到 ,得到答案;
(2)设公差为 ,根据等差数列求和公式得到 ,当 , 和 ,求出首项和公差,得
到通项公式;
(3)设 为 中所有大于0的数, 为 中所有小于0的数,故
, ,所以 .
【小问1详解】
设 成公差为r的等差数列,显然 ,
则由 得 ,
第28页/共30页
学科网(北京)股份有限公司由 得 ,解得 ,
数列 为所求3阶“归化”数列.
【小问2详解】
设等差数列 的公差为 ,
因为 ,所以 ,所以 ,即 .
当 时,此时 ,
与归化数列的条件 相矛盾.
当 时,由 ,
故 ,又 ,
联立解得 ,
所以
当 时,由 , ,同理解得 ,
所以 .
综上,当 ,
【小问3详解】
第29页/共30页
学科网(北京)股份有限公司由已知可得:必有 也必有 ( , ),
设 为 中所有大于0的数, 为 中所有小于0的数,
由已知得 , ,
所以 .
【点睛】数列不等式问题,常常需要进行放缩,放缩后变形为等差数列或等比数列,在结合公式进行证明,
又或者放缩后可使用裂项相消法进行求和,常常使用作差法和数学归纳法,技巧性较强.
第30页/共30页
学科网(北京)股份有限公司