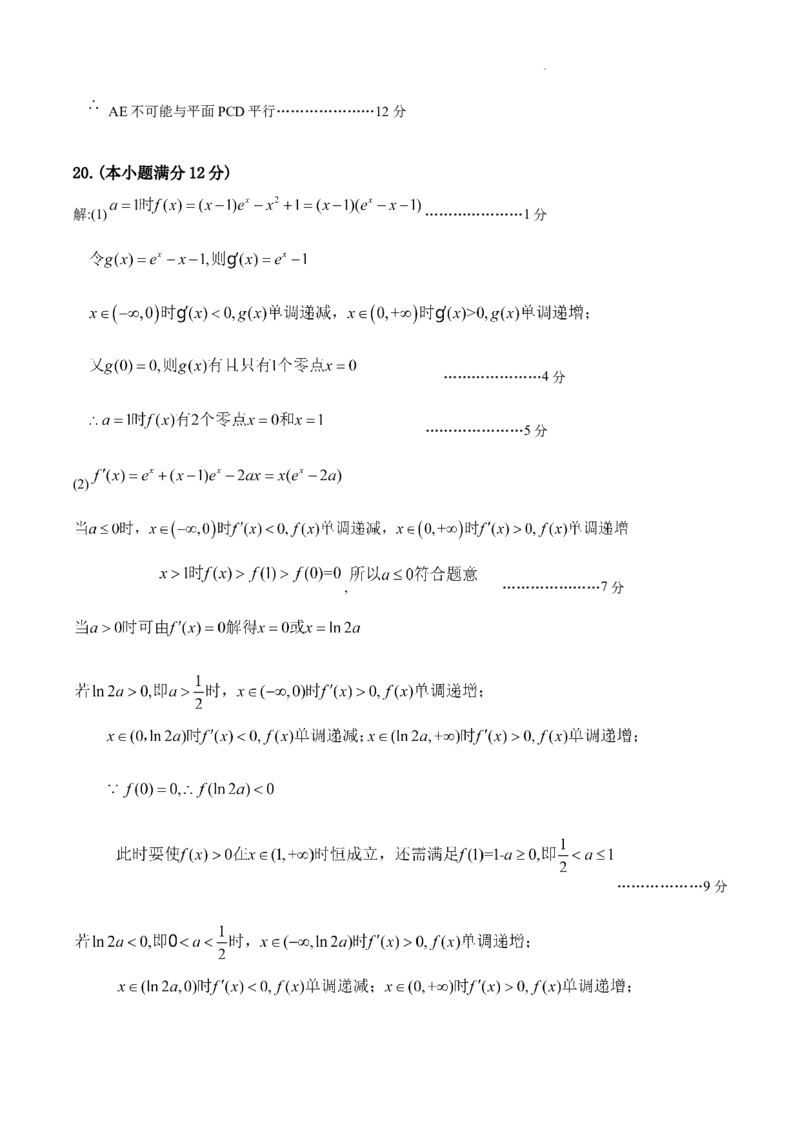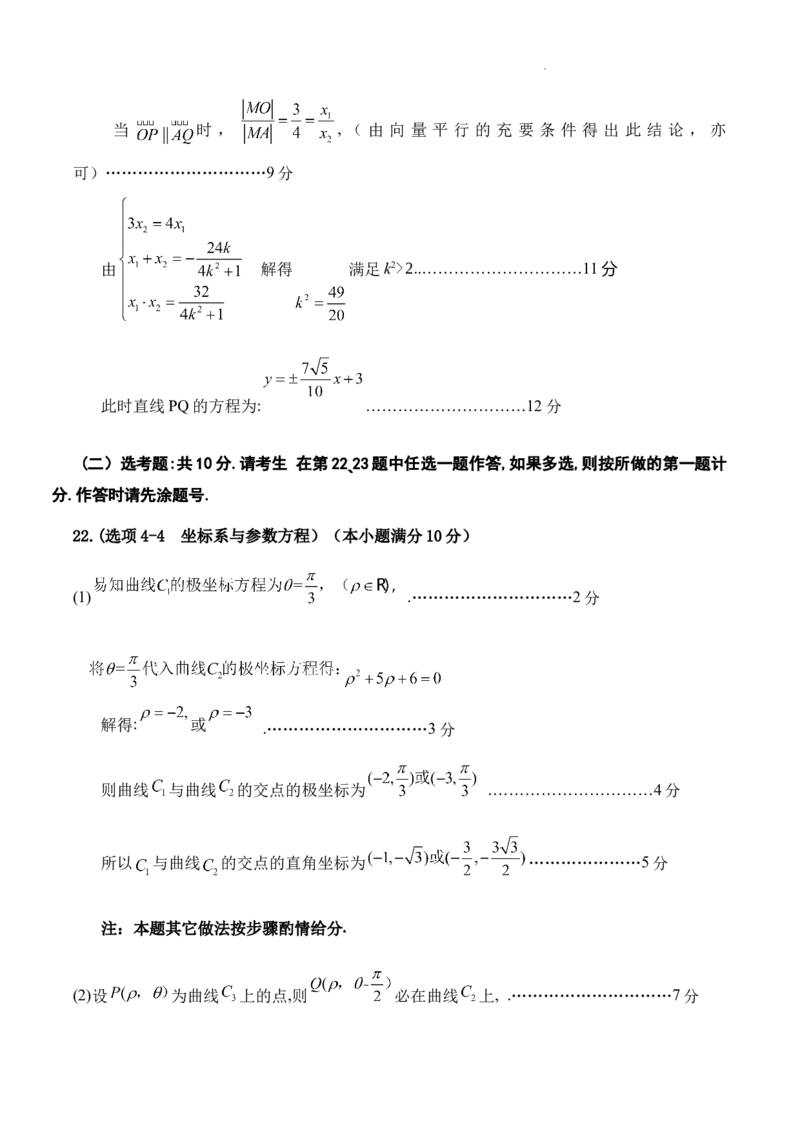文档内容
数学(文)答案
一. 选择题:(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A C D B A D B B A C C B
二:填空题:(每小题5分,共20分)
3π 2
13、 14、 15、 ±❑√15 16、 3
4 5
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分12分)
解 (1)由题意知,样本中仅乘坐 A的员工有 27+3=30(人),仅乘坐 B的员工有 24+1=
25(人),A,B两种交通工具都不乘坐的员工有5人.
故样本中A,B两种交通工具都乘坐的员工有100-30-25-5=40(人).
40
估计该公司员工中上个月A,B两种交通工具都乘坐的人数为 ×1 000=400.
100
. …………………………4分
(2)记事件C为“从样本仅乘坐B的员工中随机抽取1人,该员工上个月的交通费用大于 600
1
元 ” , 则 P(C) = = 0.04.
25
…………………………7分
(3)记事件E为“从样本仅乘坐 B的员工中随机抽查 1人,该员工本月的交通费用大于 600
元”.
假设样本仅乘坐B的员工中,本月的交通费用大于600元的人数没有变化,
则由(2)知,P(E)=0.04. …………………………10分
答案示例1:可以认为有变化.理由如下:
P(E)比较小,概率比较小的事件一般不容易发生,一旦发生,就有理由认为本月交通费
用大于600元的人数发生了变化.所以可以认为有变化. …………………………12
分
答案示例2:无法确定有没有变化.理由如下:
事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的.所以无法确
学科网(北京)股份有限公司定有没有变化. …………………………12
分
18.(本小题满分12分)
解:(1)设BC=a, …………………………2分
…………………4分
…………………………6分
(2)
,
因为 ,所以BD=2,即BC=4…………………………9分
,.…………………………11分
所以 ,即∆ABC的周长的最大值为 ………………………12分
19.(本小题满分12分)
P
(1)证明:连结AC,BD,设AC∩BD=O,
因为底面ABCD为平行四边形,则O为AC,BD的中点.
E
D C
因为PA=PC所以AC⊥PO…………………2分
O
A B
学科网(北京)股份有限公司又AC⊥PB,PB∩PO=P,PO⊆平面PBD,PB⊆平面PBD
所以AC⊥平面PBD.…………………4分
又BD⊆平面PBD,所以AC⊥BD,
所以四边形ABCD为菱形…………………6分
方法一:(反正法)假设AE∥面PDC,
(2)
因为AB∥CD, ,所 以A∥B平面PDC,…………………8分
又
所以 平面PAB∥平面PDC. …………………10分
这显然与平面PAB与平面PDC有公共点P所矛盾.
所以假设错误,即AE不可能与面PCD平行.…………………12分
方法二:
又
…………………8分
…………………10分
…………………11分
学科网(北京)股份有限公司AE不可能与平面PCD平行…………………12分
20.(本小题满分12分)
解:(1) …………………1分
…………………4分
…………………5分
(2)
, …………………7分
………………9分
学科网(北京)股份有限公司…………………11分
…………………12分
21.(本小题满分12分)
( ❑√3)
解:(1)易知抛物线 的焦点为A(0,-1)则b=1,将 1, 代入椭圆C的方程,
2
解得a=2. 所以椭圆C的方程为+y2=1.…………………………3分
(2)ⅰ).当直线PQ的斜率不存在时可设P(x ,y ), Q(x ,-y ),又A(0,-1)
1 1 1 1
由 得 ,而这与 矛盾
所以直线PQ的斜率存在.
设直线PQ的方程为y=kx+m,P(x ,y ),Q(x ,y ).
1 1 2 2
{y=kx+m
由 X2 消去y,得(4k2+1)x2+8kmx+4m2-4=0.
+ y2=1
4
当Δ=64k2m2-4(4k2+1)(4m2-4)=16(4k2-m2+1)>0时,
x +x =-, x x =. ①
1 2 1 2
则y y =(kx +m)(kx +m)=k2x x +km(x +x )+m2=-+m2=. ②
1 2 1 2 1 2 1 2
y y =k(x +x )+2m= ③
1+ 2 1 2
由 得 ④.…………………………6分
将①②③式代入④解得m= -1,或m=3
因为直线PQ不能经过点A,所以m=3.…………………………7分
所以直线PQ方程为y=kx+3,所以直线PQ经过定点(0,3).…………………………8分
ⅱ) 设直线PQ经过的定点为M(0,3)
此时由Δ=16(4k2-m2+1)=16(4k2-8)>0,得k2>2
学科网(北京)股份有限公司当 时 , , ( 由 向 量 平 行 的 充 要 条 件 得 出 此 结 论 , 亦
可)…………………………9分
由 解得 满足k2>2..…………………………11分
此时直线PQ的方程为: …………………………12分
(二)选考题:共10分.请考生 在第22ˎ23题中任选一题作答,如果多选,则按所做的第一题计
分.作答时请先涂题号.
22.(选项4-4 坐标系与参数方程)(本小题满分10分)
(1) .…………………………2分
解得: 或
.…………………………3分
则曲线 与曲线 的交点的极坐标为 .…………………………4分
所以 与曲线 的交点的直角坐标为 …………………5分
注:本题其它做法按步骤酌情给分.
(2)设 为曲线 上的点,则 必在曲线 上, .…………………………7分
学科网(北京)股份有限公司将 代入曲线 的极坐标方程
,化为直角坐标方程为
得
所以曲线 的直角坐标方程为 .…………………………10分
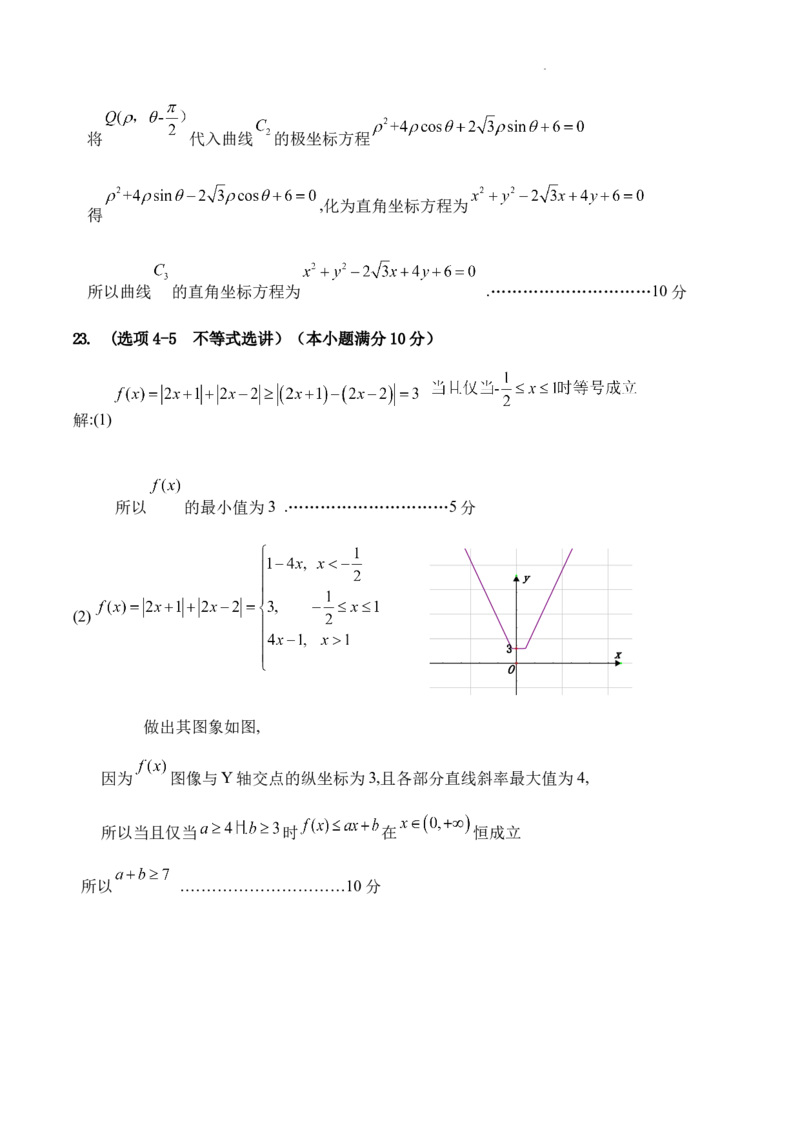
23. (选项4-5 不等式选讲)(本小题满分10分)
解:(1)
所以 的最小值为3 .…………………………5分
y
(2)
3
x
O
做出其图象如图,
因为 图像与Y轴交点的纵坐标为3,且各部分直线斜率最大值为4,
所以当且仅当 时 在 恒成立
所以 .…………………………10分
学科网(北京)股份有限公司