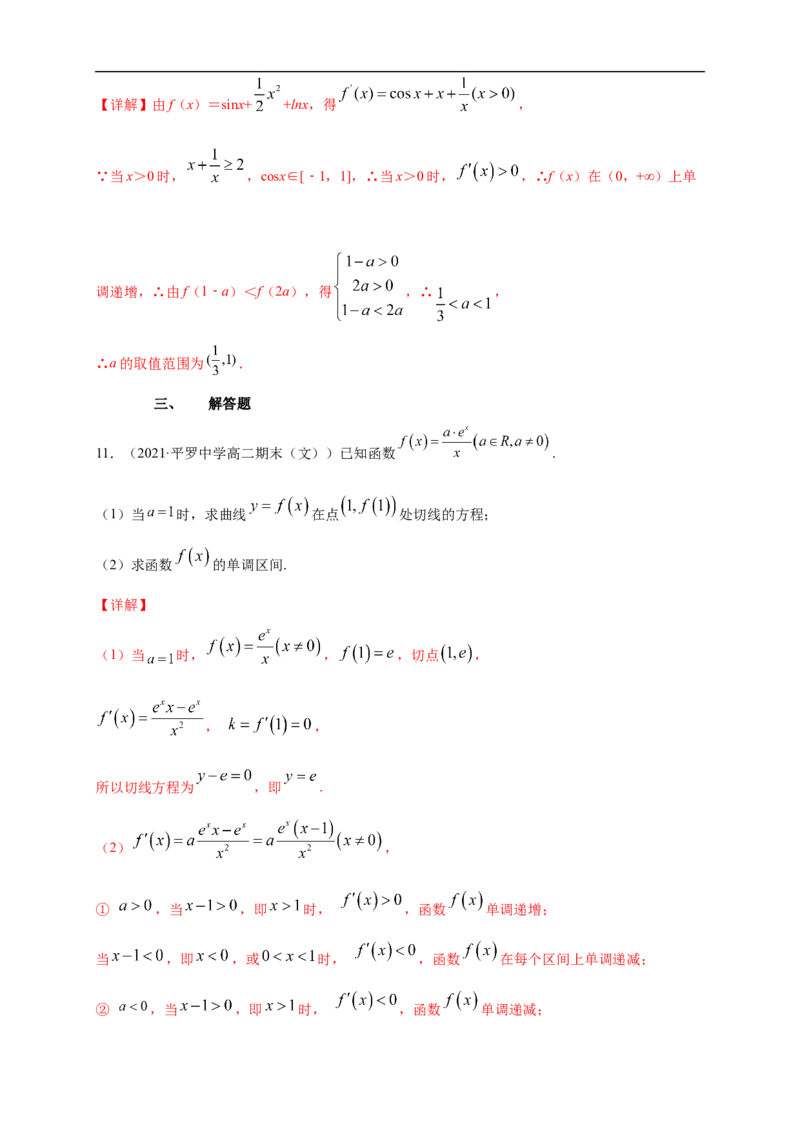文档内容
5.3.1函数的单调性(2) -A基础练
一、 选择题
1.(2021·江苏高二课时练)函数 的单调减区间为( )
A. B.
C. D.
【答案】D
【详解】 , ,令 ,解得:
或 , 的单调减区间为 .故选:D.
2.(2021·全国高二课时练)下面四个图象中,有一个是函数f(x)= x3+ax2+(a2-1)x+1(a∈R)
的导函数y=f′(x)的图象,则f(-1)等于( )
A. B.- C. D.- 或
【答案】D
【解析】∵f′(x)=x2+2ax+a2-1,∴f′(x)的图象开口向上,则②④排除.若f′(x)的图象为①,此时a
=0,f(-1)= ;若f′(x)的图象为③,此时a2-1=0,又对称轴x=-a>0,∴a=-1,∴f(-1)=
- .故选D3.(2021·全国高二课时练)已知函数 在R上是单调函数,则实数a的取
值范围是( )
A. B.
C. D.
【答案】B
【详解】由题意知, ,因为 在R上是单调函数,且 的
图象开口向下,所以 在R上恒成立,故 ,即 .
4.(2021·全国高二课时练)函数 的图像大致为 ( )
A. B.
C. D.
【答案】B
【解析】 为奇函数,舍去A, 舍去
D; ,
所以舍去C;因此选B.5.(多选题)(2020·江苏省如皋中学高二月考)设函数 ,下列条件
中,使得 有且仅有一个零点的是( )
A. B. C. D.
【答案】ABC
【详解】 ,求导得 ,当 时, , 单调递
增,当 时, ;当 时, ;由零点存在性定理知,函数
有且只有一个零点,故A,C满足题意;当 时,令 ,即 ,解得
, ,当 变化时, , 的变化情况如下表:
极大值 极小值
故当 ,函数 取得极大值 ,
当 ,函数 取得极小值
又当 时, ;当 时, ;
要使函数 有且只有一个零点,作草图
或则需 ,即 ,即 ,
B选项, ,满足上式,故B符合题意;
则需 ,即 ,即 ,
D选项, ,不一定满足,故D不符合题意;故选:ABC
6.(多选题)(2021·全国高二课时练)已知 为函数 的导函数,且
,若 ,方程 有且只有一个
根,则a的取值可能是( )
A.e B.1 C. D.
【答案】ACD
【详解】由 ,得 ,
,
∴ ,∴ ,则 ,则 ,
∴ ,方程 ,即 ,
时方程显然无解; 时,对于任意 ,函数 与 有一个交点,满足题意;
时,则 ,令 ,则 .
当 时, ,当 时, ,
∴ 在 上单调递减,在 上单调递增,
又当 时, ,当 时, .
∴ 在 时的图象如图:
由图可知, 时,方程 有一根,综上, 的取值范围为 ,故选:ACD.
二、 填空题
7.(2021·山西高二期末)函数 的单调递减区间为___________ .
【答案】
【详解】 ,令 ,解得 ,所以函数 的单调递减区间为
.
8.(2021·贵州安顺市·高二期末(文))函数 是R上的单调函数,则m的
范围是_________.
【答案】【详解】 是R上的单调函数,则导函数恒大于等于
,则 , ,故答案为:
9.(2021·全国高二课时练)已知函数 与 的图象如图所示,则函数 的单
调递减区间为___________.
【答案】 、
【详解】由图象可知,不等式 的解集为 ,
, ,由 ,可得
,解得 .因此,函数 的单调递减区间为 、
.故答案为: 、 .
10.(2021·江苏高二)已知函数f(x)=sinx+ +lnx,f(1﹣a)<f(2a),则实数a的取值范
围______.
【答案】【详解】由f(x)=sinx+ +lnx,得 ,
∵当x>0时, ,cosx∈[﹣1,1],∴当x>0时, ,∴f(x)在(0,+∞)上单
调递增,∴由f(1﹣a)<f(2a),得 ,∴ ,
∴a的取值范围为 .
三、 解答题
11.(2021·平罗中学高二期末(文))已知函数 .
(1)当 时,求曲线 在点 处切线的方程;
(2)求函数 的单调区间.
【详解】
(1)当 时, , ,切点 ,
, ,
所以切线方程为 ,即 .
(2) ,
① ,当 ,即 时, ,函数 单调递增;
当 ,即 ,或 时, ,函数 在每个区间上单调递减;
② ,当 ,即 时, ,函数 单调递减;当 ,即 ,或 时, ,函数 在每个区间上单调递增;
综上所述, 时, 的单调递增区间为 ,单调递减区间为 , ;
时, 的单调递增区间为 , ,单调递减区间为 .
12.(2021·安徽省舒城中学高二期末)已知 .
(1)当 时,求 的单调区间
(2)若f(x)存在3个零点,求实数a的取值范围.
【详解】
(1)当 时,
由 ,得 ,由 ,得 ,
所以 在 单调递减,在 上单调递增
(2)由函数 ,
可得 有一个零点 ,
要使得 有3个零点,即方程 有2个实数根,
又由方程 ,可化为 ,
令 ,即函数 与 图象 有两个交点,
令 ,得 ,的单调性如表:
1
- - 0 + +
↘ ↘ 极小值 ↗ ↗
所以函数 在 处取得极小值2e,
当 时, ,又 , 的大致图象如图,
由函数 与 图象有两个交点,根据图象可得
所以要使得 有3个零点,则实数 的取值范围为