专题18等比数列（原卷版）_E015高中全科试卷_数学试题_选修2_06.专项练习_专题18等比数列-高中数学新教材人教A版选择性必修配套提升训练

专题18 等比数列 一、单选题 a  n S a 2a a 1 S  1．（2020·陕西省高三三模（理））已知等比数列 n 的前 项和为 n， 4 3， 1 ，则 4 （ ） A．31 B．15 C．8 D．7 a  aa a 8 a a  2.（2020·毕节市实验高级中学高一期中）在等比数列 n 中，已知 1 3 11 ，那么 2 8 （ ） A．4 B．6 C．12 D．16 a  S a 1 a 4S 0 S 3．（2020·江西省高三三模（文））已知等比数列 n 的前n项和为 n，若 1 ， 3 2 ，则 n （ ） 512 1024 A． B．512 C．1024 D． a  aa 4 a 256 a  4．（2020·河南省高三月考（文））在等比数列 n 中，已知 1 3 ， 9 ，则 8 （ ） 64 128 A．128 B．64 C．64或 D．128或 a  3 a ,a ,a a 5．（2020·毕节市实验高级中学高一期中）已知等差数列 n 的公差为 ,若 1 3 4成等比数列,则 2等 于() A．9 B．3 C．-3 D．-9 a  n S a 2, a 2a a 0 6．（2020·湖北省高三三模（理））设等比数列 n 的前 项和为 n， 1 2 3 4 ，则 S  5 （ ） A．2 B．0 C．2 D．4 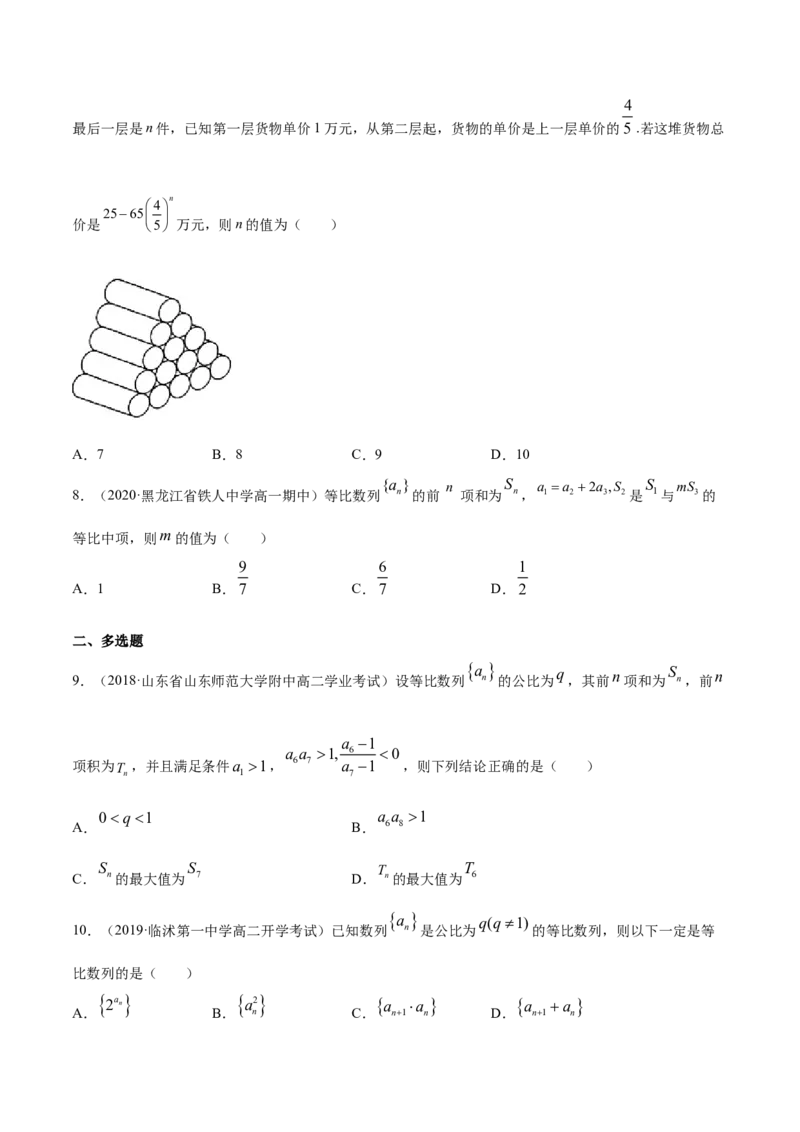7．（2020·福建省高二期末）“垛积术”（隙积术）是由北宋科学家沈括在《梦溪笔谈》中首创，南宋数 学家杨辉、元代数学家朱世杰丰富和发展的一类数列求和方法，有菱草垛、方垛、刍童垛、三角垛等等， 某仓库中部分货物堆放成如图所示的“菱草垛”：自上而下，第一层1件，以后每一层比上一层多1件，4 最后一层是n件，已知第一层货物单价1万元，从第二层起，货物的单价是上一层单价的5 .若这堆货物总 4 n 2565  价是 5 万元，则n的值为（ ） A．7 B．8 C．9 D．10 {a } n S a a 2a ,S S mS 8．（2020·黑龙江省铁人中学高一期中）等比数列 n 的前 项和为 n， 1 2 3 2是 1与 3的 m 等比中项，则 的值为（ ） 9 6 1 A．1 B．7 C．7 D．2 二、多选题 a  q n S n 9．（2018·山东省山东师范大学附中高二学业考试）设等比数列 n 的公比为 ，其前 项和为 n，前 a 1 a a 1, 6 0 项积为T ，并且满足条件a 1， 6 7 a 1 ，则下列结论正确的是（ ） n 1 7 0q1 a a 1 A． B． 6 8 S S T T C． n的最大值为 7 D． n的最大值为 6 a  q(q 1) 10．（2019·临沭第一中学高二开学考试）已知数列 n 是公比为 的等比数列，则以下一定是等 比数列的是（ ）  2a n   a2 a a  a a  A． B． n C． n1 n D． n1 n11．（2020·山东省曲阜一中高三月考）在《增删算法统宗》中有这样一则故事：“三百七十八里关，初行 健步不为难；次日脚痛减一半，如此六日过其关.”则下列说法正确的是（ ） 1 A．此人第二天走了九十六里路 B．此人第三天走的路程站全程的8 C．此人第一天走的路程比后五天走的路程多六里 D．此人后三天共走了42里路 a a a a a a a a a a a 2 12．（2019·山东省高三月考）已知 1， 2， 3， 4成等比数列，满足 1 2 3 4 2 3 4 ， a 1 且 4 ，下列选项正确的是（ ） a a a a a a a a A． 1 3 B． 3 4 C． 1 2 D． 2 4 三、填空题 13．（2018·平遥县综合职业技术学校高二期中）两个数等差中项是20，等比中项是12，则这两个数是 ________. {a } a a 1 a a 2 14．（2020·毕节市实验高级中学高一期中）在等比数列 n 中， 1 2 ， 3 4 ，则 a a a a  5 6 7 8 ________. n a  15．（2020·湖南省高三三模（理））在数列 a  中，a 4，且a 2a ，则 2i __________. n 4 n2 n i1 16．（2020·进贤县第一中学高一月考）我国古代数学著作《九章算术》有如下问题：“今有蒲（水生植物 名）生一日，长三尺；莞（植物名，俗称水葱、席子草）生一日，长一尺．蒲生日自半，莞生日自倍．问 几何日而长等？”意思是：今有蒲生长1日，长为3尺；莞生长1日，长为1尺．蒲的生长逐日减半，莞 的生长逐日增加1倍．若蒲、莞长度相等，则所需的时间约为_____日． （结果保留一位小数，参考数据： ， ） lg20.30 lg30.48 四、解答题 a  S a +1 17．（2020·江西省高二月考（理））已知数列 n 是公差为2的等差数列，它的前n项和为 n，且 1 ， a 1 a 1 3 ， 7 成等比数列。a  (1)求 n 的通项公式。  1    (2)求数列  S  的前n项和 T 。 n n a  S 18．（2020·湖北省江夏实验高中高一期中）已知等差数列 n 的前n项和为 n，且 a 3,S 49,nN* 2 7 a  (1)求数列 n 的通项公式； (a 1)2n1 (2)设 b n  n n ，求数列 b n  的前n项和T n. a 19．（2020·江苏省如皋中学高一月考）已知数列 a n  的前n项和 S n 满足 S n  a1 a n 1 ，(a为常数， a0 a1 且 ， ). a  （1）求数列 n 的通项公式； 2S b  n 1 （2）设 n a ，若数列 b  为等比数列，求a的值. n n a  a nS b a 1 20．（2020·广东省高三一模（文））已知数列 n 的前n项和为S，且满足 n n，设 n n ． n a ,a ,a （1）求 1 2 3； b  （2）判断数列 n 是否是等比数列，并说明理由； a  （3）求数列 n 的前n项和S． n a  n S 21．（2019·福建省莆田一中高三月考（文））设数列 n 前 项和为 ，且满足1 1 a  ,S a   nN* 1 32 n n1 32 ． a  a  （1）证明 n 为等比数列，并求数列 n 的通项公式；   （2）在（1）的条件下，设 b n log 2 a n，求数列 b n 的前n项和T n ． a  a 1 a 3 22．（2020·宁夏回族自治区银川九中高三二模（文））在数列 n 中， 1 ， 2 ， a 3a 2a 0 nN n2 n1 n n1 （ 且 ）. a a  （1）证明：数列 n1 n 是等比数列； a  （2）求数列 n 的通项公式.