文档内容
专题 3.3 幂函数
1 幂函数的定义
一般地,形如y=xα的函数称为幂函数,其中x是自变量,α为常数.
注 (1)注意幂函数中xα的系数是1,底数是变量x,指数α是常数;
2正数的正分数指数幂的意义
(1)正数的正分数指数幂的意义,规定: m
an =√n am (a>0,m,n∈N∗,且n>1)
巧记“子内母外”(根号内的m作分子,根号外的n作为分母)
m
− 1 1
(2)正数的正分数指数幂的意义:a n = = (a>0,m,n∈N∗,且n>1)
m √n am
an
(3)0的正分数指数幂等于0,0的负分数指数幂没有意义.
3 幂函数图像及其性质
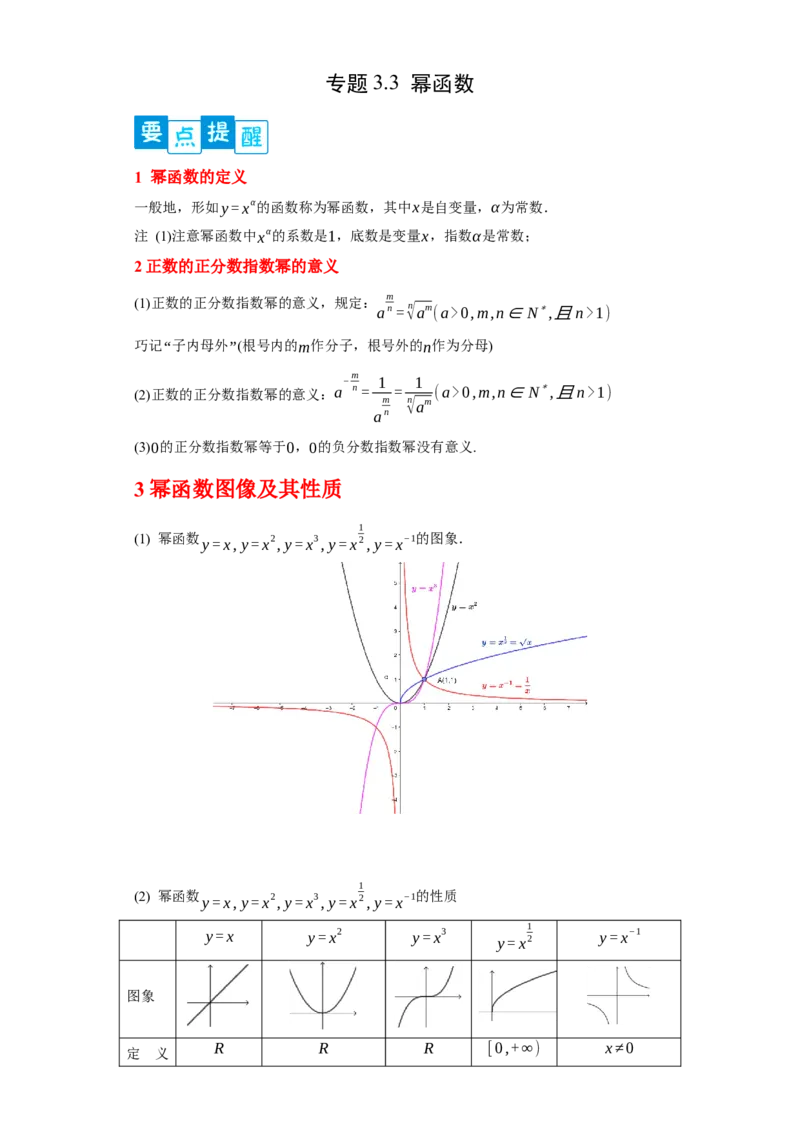
1
(1) 幂函数 y=x,y=x2,y=x3,y=x2,y=x−1的图象.
1
(2) 幂函数 y=x,y=x2,y=x3,y=x2,y=x−1的性质
1
y=x y=x2 y=x3
y=x2
y=x−1
图象
X|X|K]
定 义
R R R [0,+∞) x≠0域
值域 R [0,+∞) R [0,+∞) x≠0
奇 偶
奇函数 偶函数 奇函数 非奇非偶 奇函数
性
在 (−∞,0]上 递 在 (−∞,0)上 递
单 调 在[0,+∞)
在R上递增 减 在R上递增 减
性 上递增
在(0,+∞)上递增 在(0,+∞)上递减
定点 (1,1),(0,0) (1,1),(0,0) (1,1),(0,0) (1,1),(0,0) (1,1)
(3)性质
① 所有的幂函数在(0 , +∞ )都有定义,并且图象都过点(1 , 1);
② α>0时,幂函数的图象通过原点,并且在[0 , +∞ )上是增函数.
特别地,当α>1时,幂函数变化快,图象下凹;当0<α<1时,幂函数变化慢,图象上
凸.
③ α<0时,幂函数的图象在(0 , +∞ )上是减函数.在第一象限内,当x从右边趋
向原点时,图象在y轴右方无限地逼近y轴正半轴,当x趋于+∞时,图象在x轴上方无
限地逼近x轴正半轴.
一、单选题
1.幂函数 在 上单调递减,则实数m的值为( )
A. B.3 C. 或3 D.
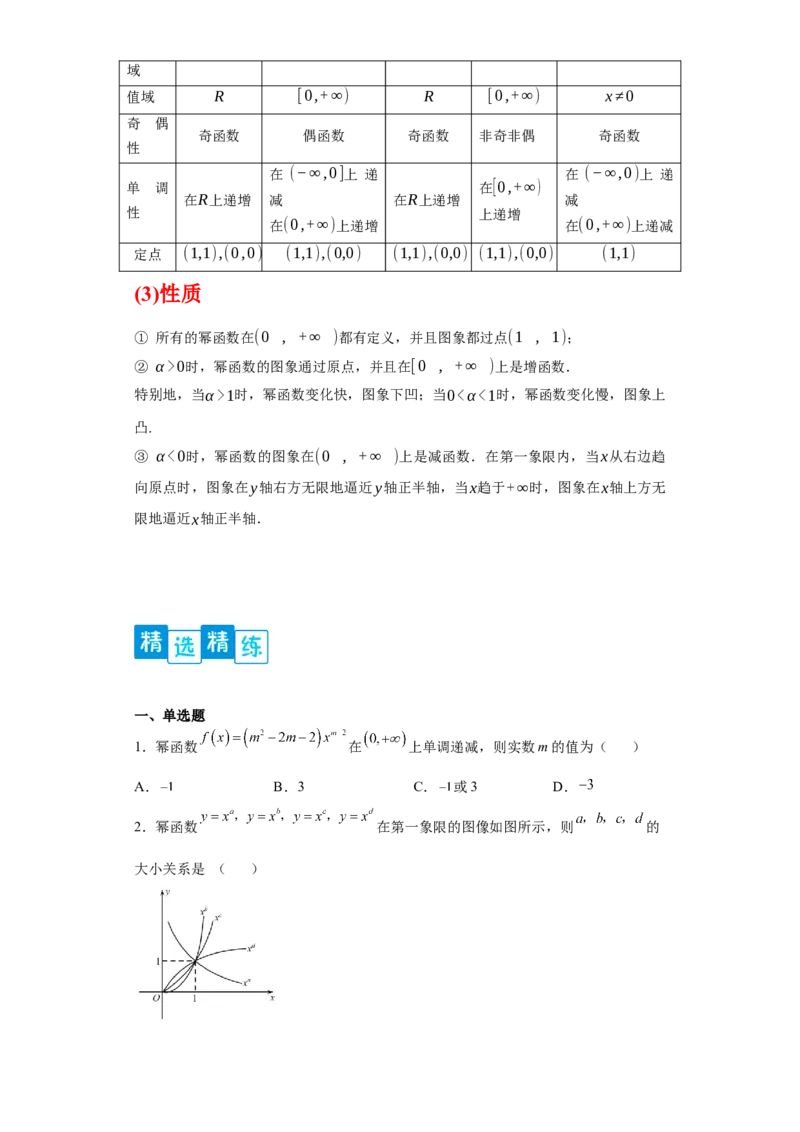
2.幂函数 在第一象限的图像如图所示,则 的
大小关系是 ( )A. B. C. D.
3.已知幂函数 与 的部分图像如图所示,直线 , 与
, 的图像分别交于A,B,C,D四点,且 ,则
( )
A. B. C. D.
4.已知幂函数 在 上单调递减,设 ,
, ,则( )
A. B.
C. D.
5.设 , , , ,则这四个数的大小关系是( )
A. B. C. D.
6.设 , , ,则( )
A. B. C. D.
7.已知函数 ,若 ,则实数a的取值范围是
( )A. B. C. D.
8.幂函数 在区间 上单调递增,且 ,则
的值( )
A.恒大于0 B.恒小于0
C.等于0 D.无法判断
9.已知函数 是减函数,则实数a的取值范围是( )
A. B. C. D.
10.设 ,若 ,则
A.2 B.4 C.6 D.8
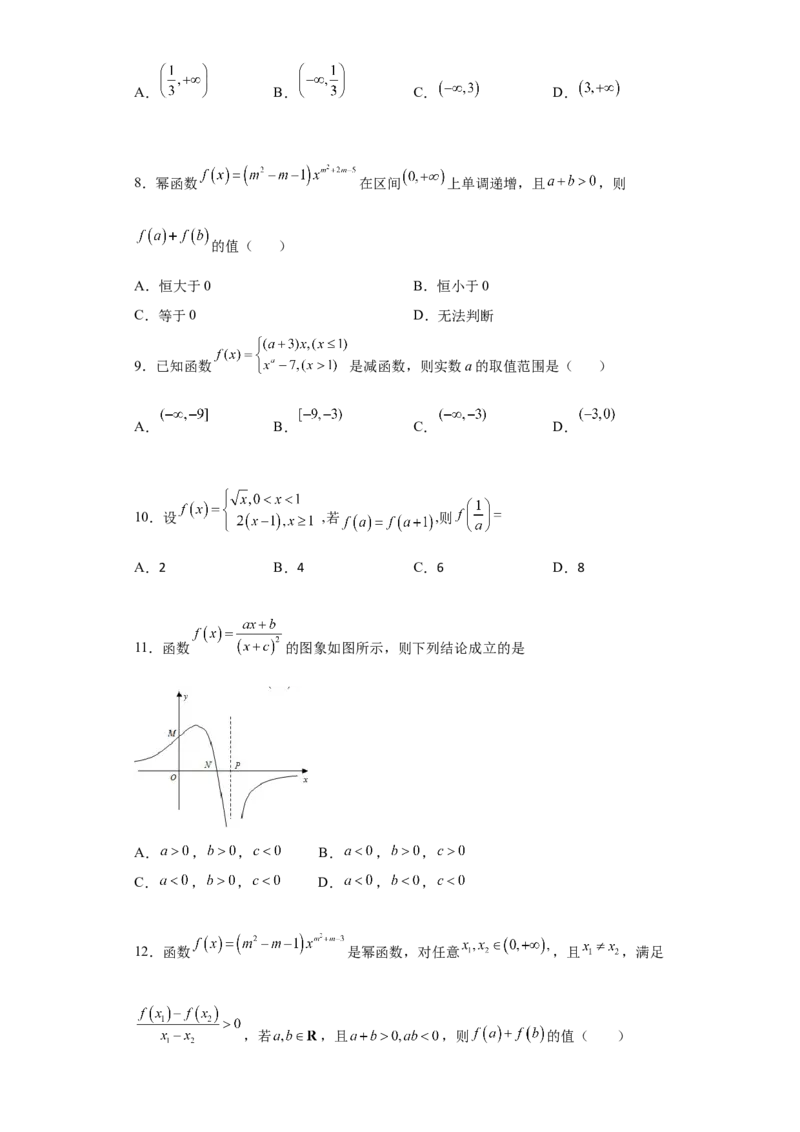
11.函数 的图象如图所示,则下列结论成立的是
A. , , B. , ,
C. , , D. , ,
12.函数 是幂函数,对任意 ,且 ,满足
,若 ,且 ,则 的值( )A.恒大于0 B.恒小于0 C.等于0 D.无法判断
13.已知 是定义域为 的奇函数,满足 .若 ,则
A. B. C. D.
14.若幂函数 的图象过点 ,则函数 的最大值为
( )
A. B. C. D.
二、填空题
15.已知幂函数 在 上单调递减,则 ______.
16.已知幂函数 的图像关于y轴对称,且在 上是减函
数,实数 满足 ,则 的取值范围是_____.
17.写出一个同时具有下列性质①②③的函数 ______.
① ;② ;③任取 , , 且
.
18.已知 是奇函数,当 时, ,则 ______.
19.已知幂函数 的图象关于 轴对称,且在 上单调递减,
则满足 的 的取值范围为________.
20.若幂函数 过点 ,则满足不等式 的实数 的取值范
围是______